Le test d'ajustement du chi-carré est une méthode simple pour vérifier l'hypothèse selon laquelle une série de données donnée suit une distribution normale. Dans ce guide, vous apprendrez comment effectuer le test du chi-carré dans Excel pour déterminer si les ventes de smartphones suivent une distribution normale. Nous vous guiderons pas à pas à travers le processus, allant de la création d'un tableau de fréquences classées jusqu'au calcul de la statistique de test et à la comparaison avec la valeur critique du chi-carré.
Principales conclusions
- Le test d'ajustement du chi-carré aide à vérifier les distributions normales.
- Il est important de créer un tableau de fréquences classées.
- La statistique de test est comparée à une valeur critique pour rejeter ou accepter l'hypothèse nulle.
Guide étape par étape
Étape 1: Préparer les données
Pour réaliser le test du chi-carré, vous avez besoin des données. Copiez les ventes de smartphones dans une feuille de calcul Excel. Assurez-vous que vos données sont organisées dans une seule colonne.

Étape 2: Créer un histogramme
Pour obtenir des indications visuelles sur la distribution, créez un histogramme de vos données. Accédez à "Insérer" et sélectionnez "Graphiques". Ajoutez un histogramme en sélectionnant la plage de données.
Étape 3: Créer un tableau de fréquences classées
Pour le test du chi-carré, vous avez besoin d'un tableau de fréquences classées. Déterminez d'abord le nombre de classes pour votre tableau - dans ce cas, nous utilisons six classes. Calculez la largeur des intervalles et créez le tableau en conséquence.
Étape 4: Calculer les fréquences
Vous devez maintenant calculer les fréquences observées pour chaque classe. Accédez à "Analyse des données" dans le menu et sélectionnez "Histogramme". Choisissez la plage d'entrée pour vos données et les limites de classe. Déterminez la plage de sortie pour le tableau de fréquences.
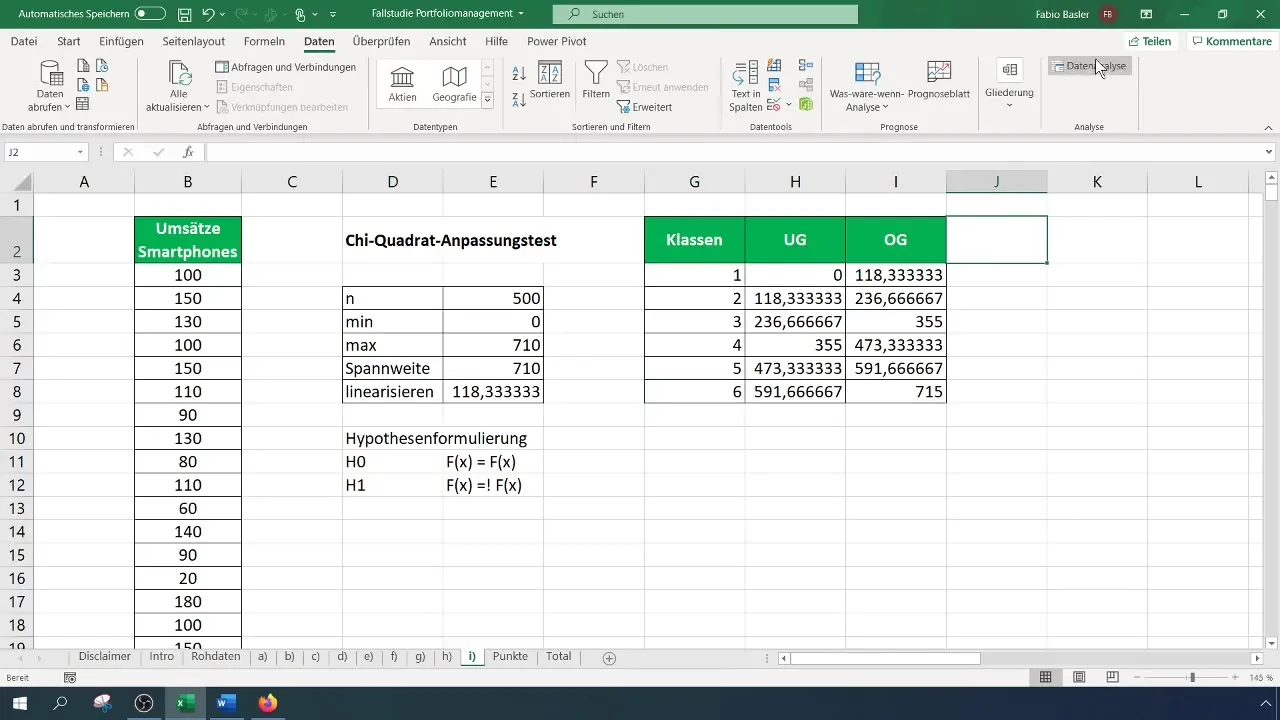
Étape 5: Calculer les fréquences attendues
Pour calculer les fréquences attendues, calculez les probabilités pour chaque classe basées sur la distribution normale supposée. Pour cela, vous avez besoin de la moyenne et de l'écart type de vos données.
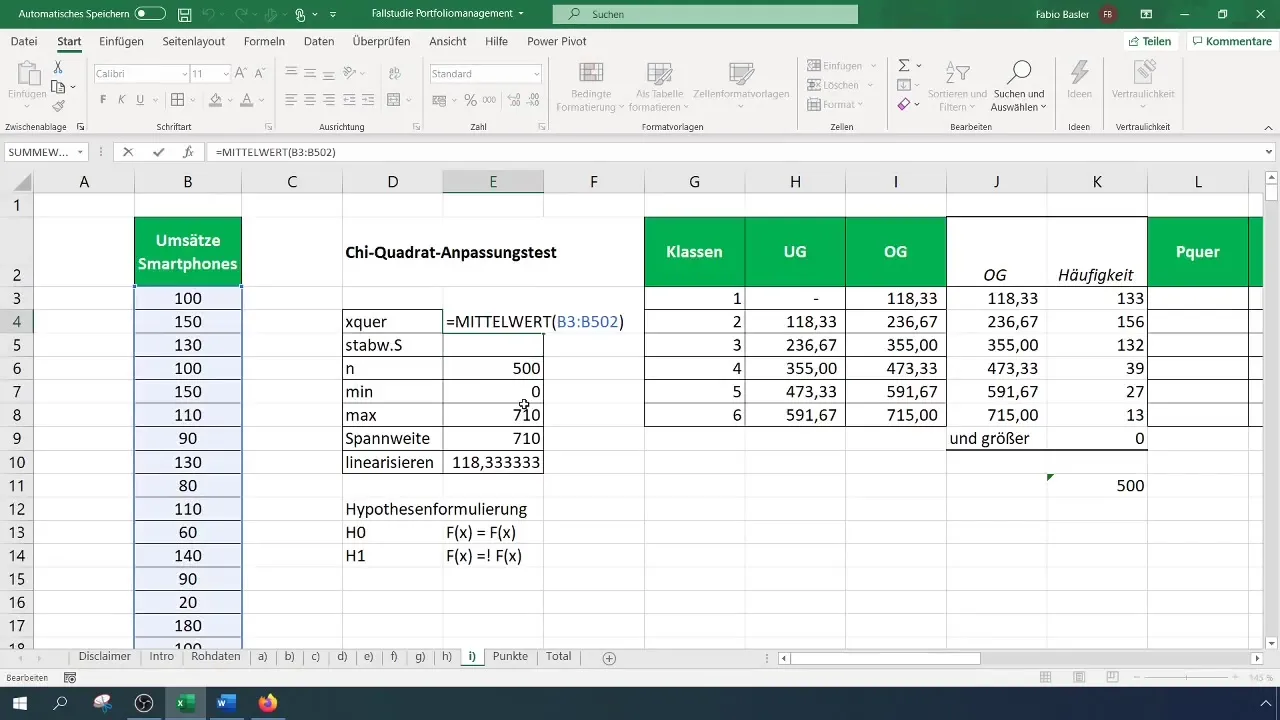
Étape 6: Calculer la statistique de test
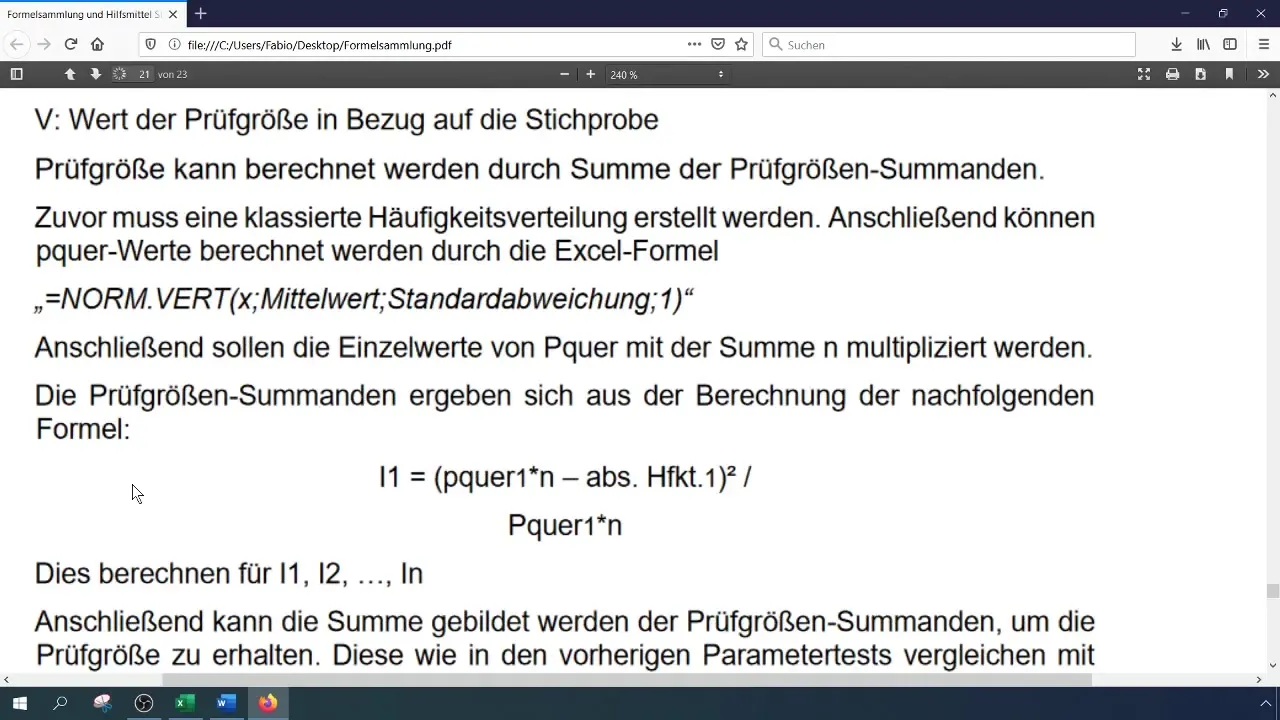
Calculez la statistique de test (chi-carré) avec la formule suivante :
[ \chi^2 = \sum \frac{(O_i - E_i)^2}{E_i} ]
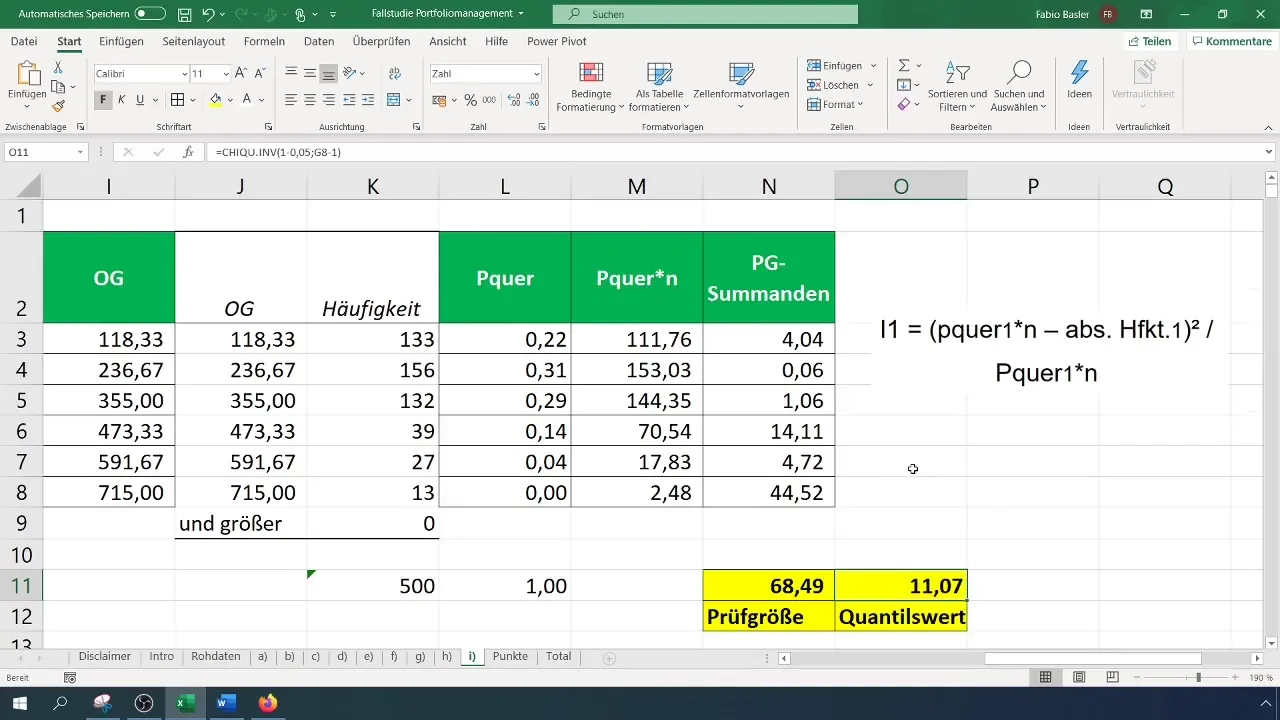
où (O_i) sont les fréquences observées et (E_i) sont les fréquences attendues. Vous pouvez effectuer ce calcul dans Excel en enregistrant les différentes composantes dans des cellules distinctes.
Étape 7: Calculer la valeur critique
Pour évaluer la statistique de test, vous devez calculer la valeur critique ( \chi^2 ) pour votre niveau de confiance et le nombre de degrés de liberté. Le nombre de degrés de liberté pour le test du chi-carré est (k - 1), où (k) est le nombre de classes.
Étape 8: Vérifier les hypothèses
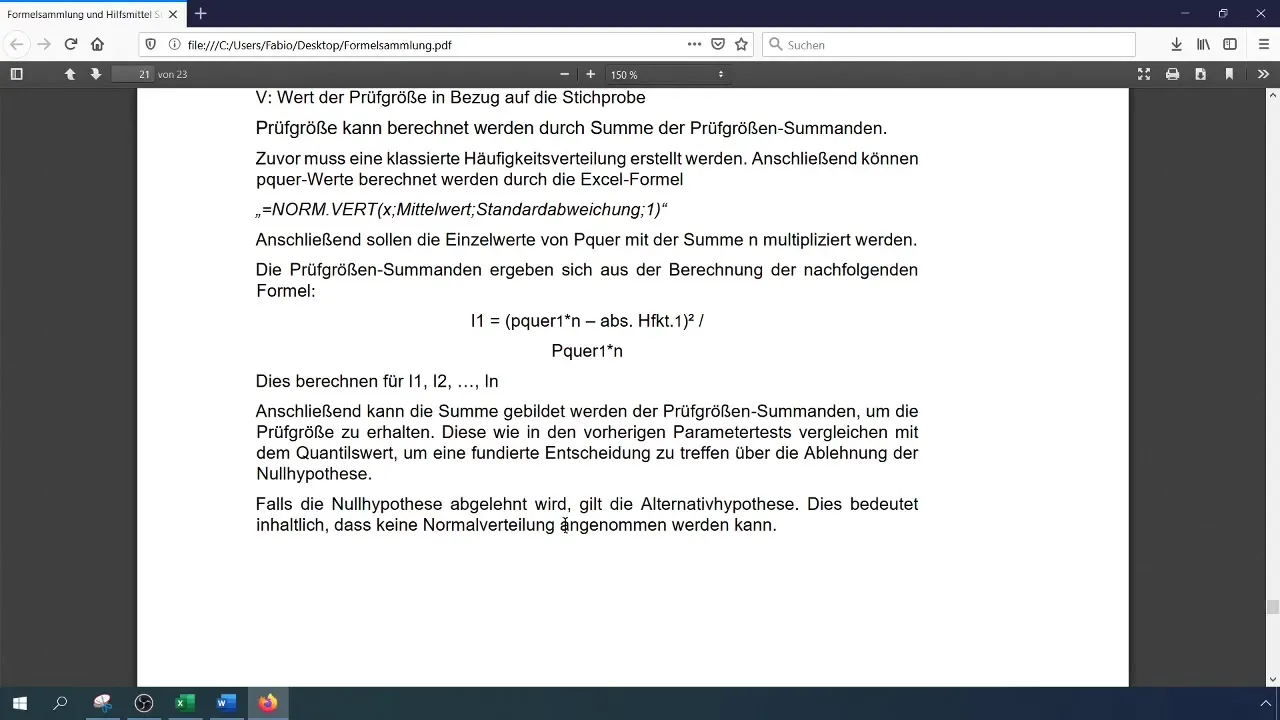
Comparez votre statistique de test calculée avec la valeur critique. Si la statistique de test est supérieure à la valeur critique, rejetez l'hypothèse nulle, ce qui signifie que les données ne sont pas normalement distribuées. Sinon, acceptez l'hypothèse nulle.
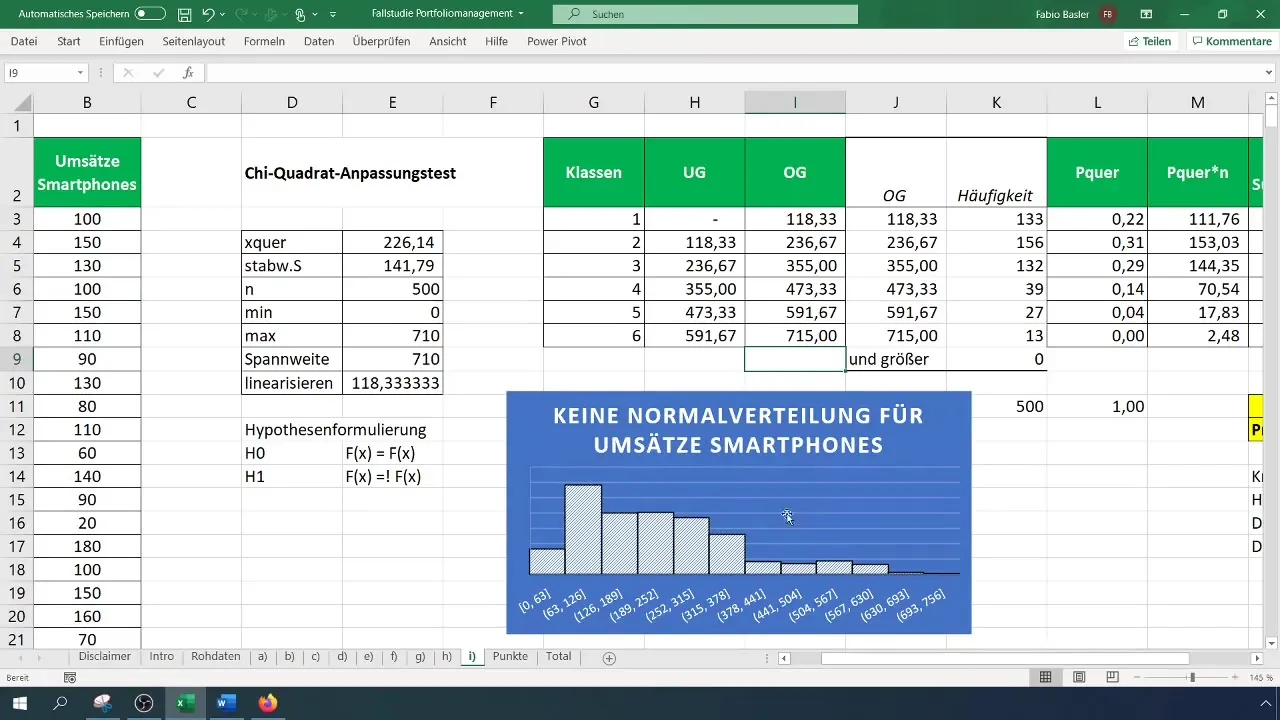
Étape 9: Résumer les résultats
Conservez vos résultats et complétez-les avec les données graphiques et les tests d'hypothèse. N'oubliez pas de vérifier votre histogramme pour confirmer visuellement que la distribution n'est pas normale.
Résumé
Au cours de ce guide, vous avez appris comment exécuter le test d'ajustement du chi carré dans Excel pour analyser la distribution normale de vos revenus de smartphone. Les étapes comprennent la création d'un tableau de fréquences classées, le calcul des fréquences attendues, de la statistique de test et enfin la comparaison avec la valeur critique.
Questions fréquemment posées
Qu'est-ce que le test d'ajustement du chi carré?Le test d'ajustement du chi carré vérifie si la distribution de fréquence observée correspond à une distribution normale.
Combien de classes faut-il pour le tableau de fréquences?En général, 5 à 10 classes sont recommandées pour analyser les données de manière significative.
Que faire si l'hypothèse nulle est rejetée?Si vous rejetez l'hypothèse nulle, cela signifie que les données ne sont pas distribuées de manière normale.
Comment calculer la valeur critique du chi carré?La valeur critique est lue dans un tableau de distribution du chi carré en fonction des degrés de liberté et du niveau de signification souhaité.


