Il est essentiel de prendre des décisions éclairées dans le domaine des affaires et des ventes sur la base d'analyses de données. Un intervalle de confiance bilatéral te permet de déterminer la plage dans laquelle la vraie valeur moyenne d'un paramètre peut être trouvée avec une certaine probabilité. Dans ce guide, je vais te montrer comment calculer, à l'aide d'Excel, les intervalles des limites de l'intervalle pour le chiffre d'affaires hebdomadaire d'une équipe de vente avec une probabilité de confiance de 93 %.
Principales conclusions
Les aspects essentiels de l'intervalle de confiance bilatéral comprennent :
- Le calcul de la moyenne comme estimée du paramètre.
- Détermination de l'écart-type de l'échantillon.
- Application des formules pour déterminer les limites inférieures et supérieures de l'intervalle.
- Prise en compte de la probabilité de confiance pour situer l'intervalle.
Guide étape par étape
En premier lieu, il est nécessaire d'avoir une compréhension solide des termes et des étapes qui définissent ce processus.
Étape 1 : Préparation des données
Tout d'abord, tu dois préparer les données pour l'équipe de vente A. Filtre les données pertinentes et copie-les dans ton document Excel.
Étape 2 : Calcul de la moyenne
Pour calculer l'intervalle de confiance, la première étape consiste à déterminer la moyenne, qui sert d'estimation du chiffre d'affaires attendu. Dans Excel, tu peux le faire avec la formule =MOYENNE(Plage), où « Plage » est la ou les cellules contenant les données sur le chiffre d'affaires hebdomadaire de l'équipe de vente A.
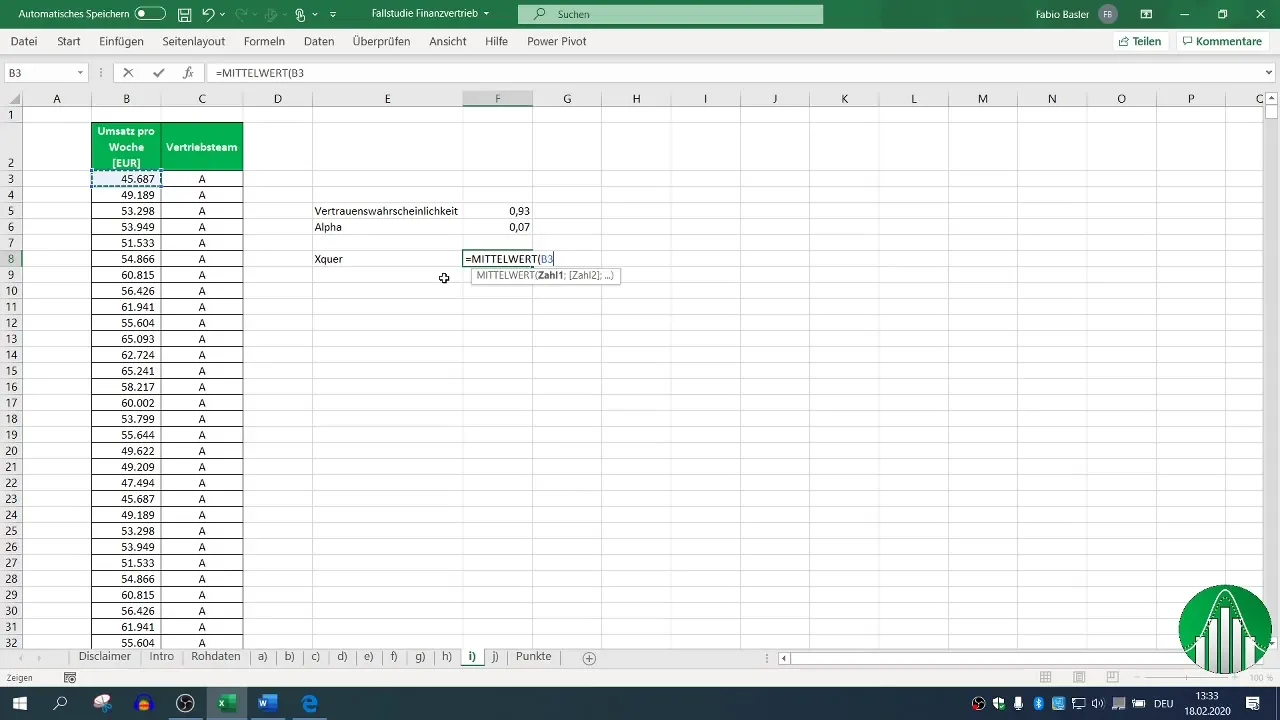
Étape 3 : Calcul de l'écart-type
L'écart-type (σ) est important pour le calcul de l'intervalle de confiance bilatéral. Tu peux le calculer dans Excel avec la formule =ECARTYPE.S(Plage). Assure-toi de choisir la formule appropriée pour l'écart-type de l'échantillon.
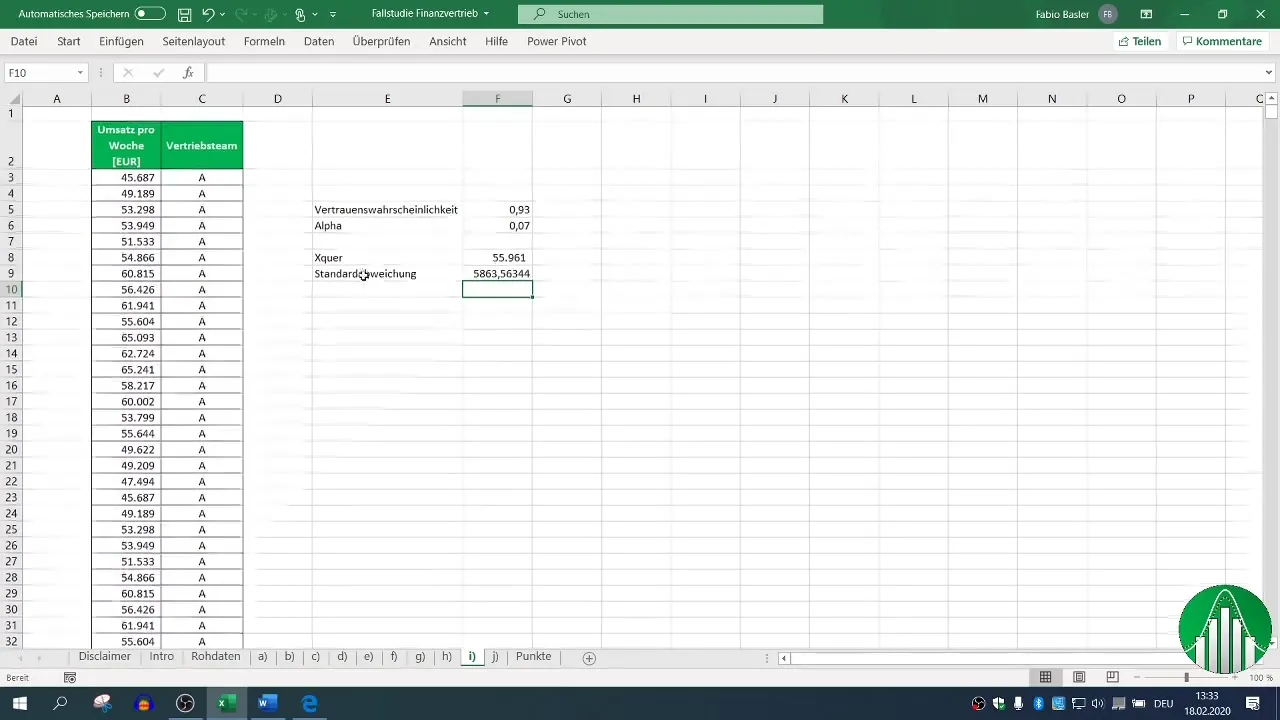
Étape 4 : Détermination de la taille de l'échantillon
Ensuite, tu dois déterminer la taille de l'échantillon (n). Additionne le nombre de données que tu as collectées pour l'équipe de vente A. Dans cet exemple, nous partons de 33 données.
Étape 5 : Calcul de l'écart-type de la moyenne (σ_m)
Pour calculer l'intervalle de confiance, il est nécessaire de calculer l'écart-type de la moyenne, simplement l'écart-type divisé par la racine carrée de la taille de l'échantillon.
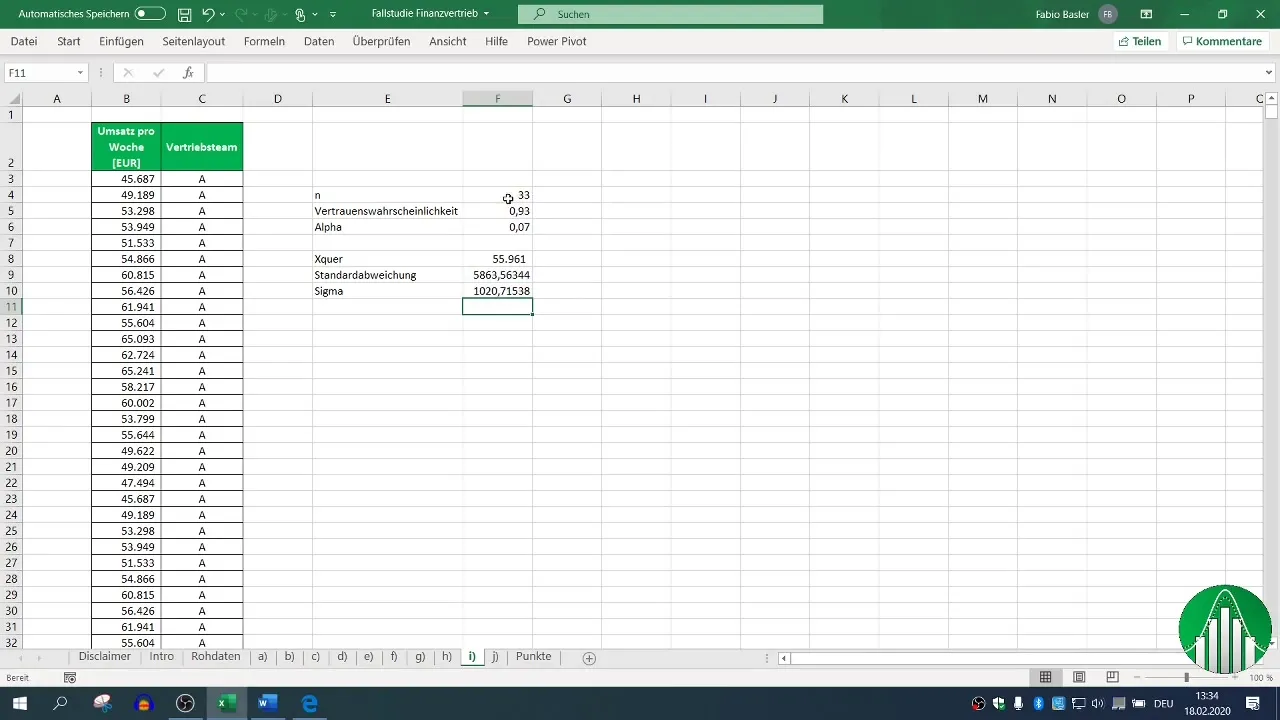
Étape 6 : Détermination du quantile
Pour calculer l'intervalle de confiance bilatéral, tu as besoin du quantile. Comme tu spécifies une probabilité de confiance de 93 %, α est de 7 % et la distribution du quantile se trouve en utilisant la fonction Excel.
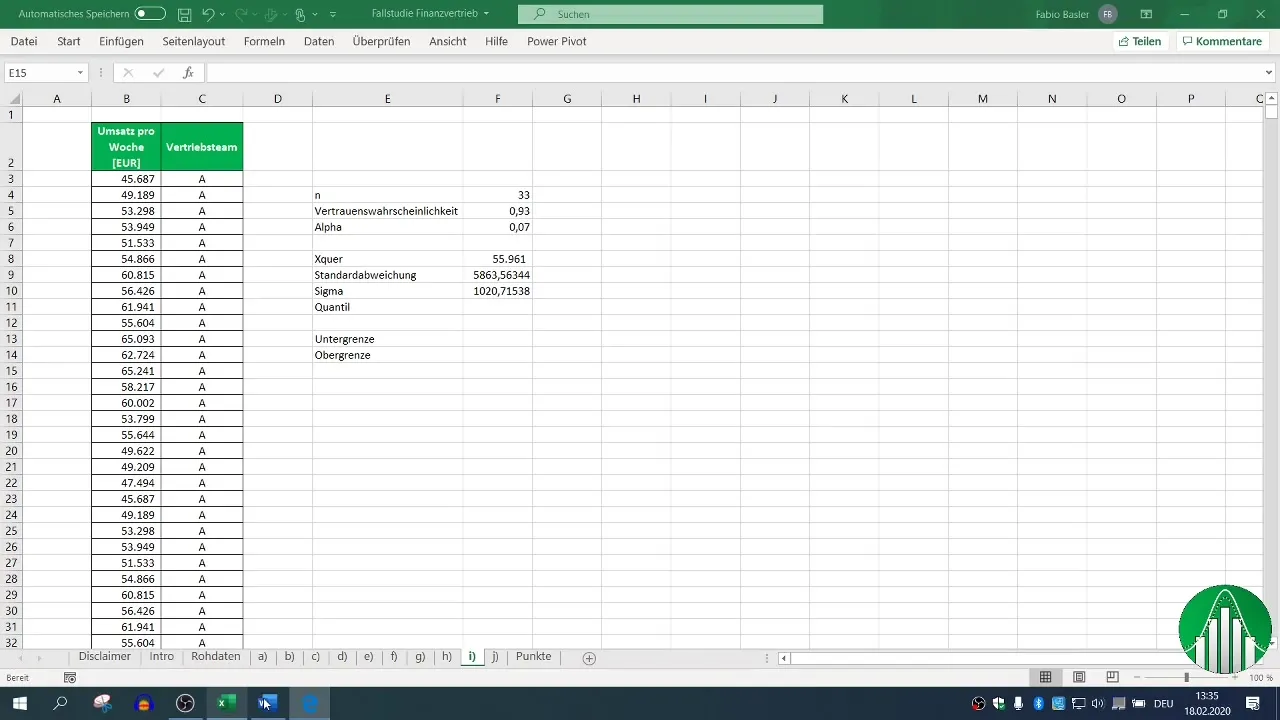
Étape 7 : Calcul de la limite inférieure
Nous calculons maintenant la limite inférieure de l'intervalle de confiance. Pour cela, tu soustrais du moyen (x̄) le produit du quantile et de l'écart-type de la moyenne.
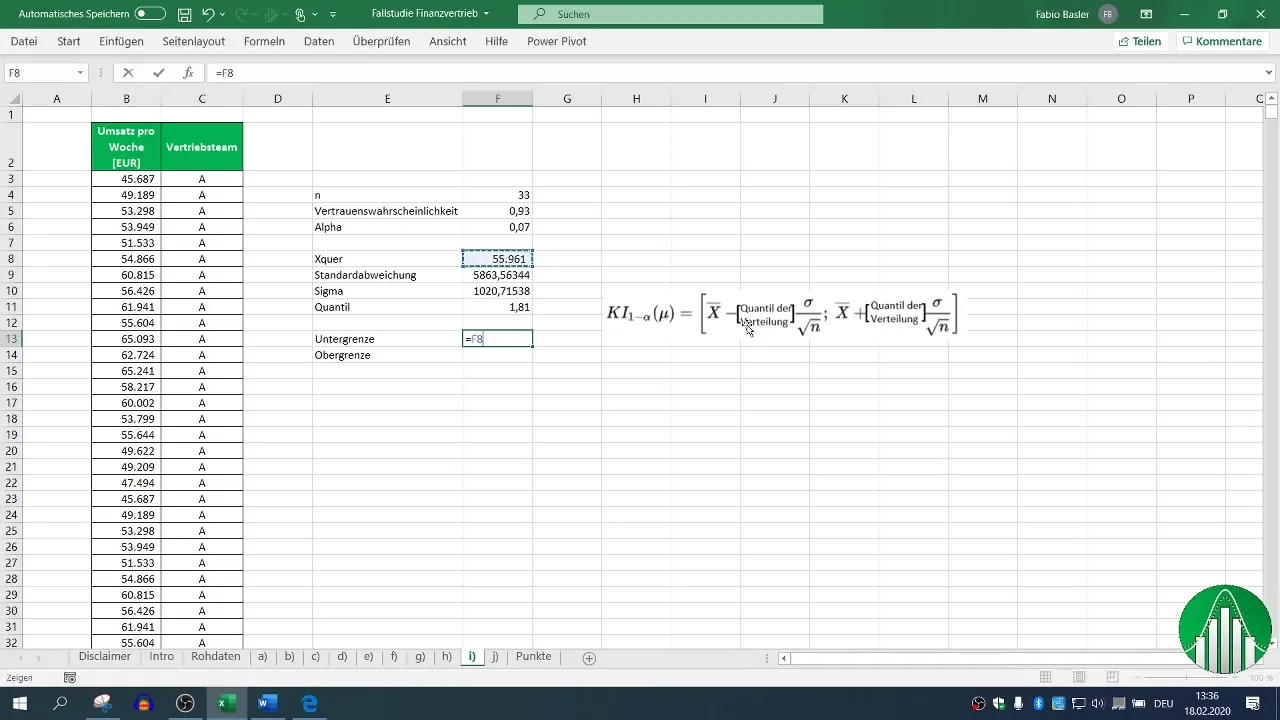
Étape 8 : Calcul de la limite supérieure
La limite supérieure est calculée de manière similaire, mais tu ajoutes le produit plutôt que de soustraire.
Étape 9 : Interprétation des résultats
Après ces calculs, tu obtiens l'intervalle de confiance bilatéral pour le chiffre d'affaires hebdomadaire de l'équipe de vente A. Dans notre exemple, l'intervalle se situe entre 54,111 et 57,810. Cela signifie qu'avec une probabilité de confiance de 93 %, la vraie valeur moyenne du chiffre d'affaires se trouve dans cette plage.
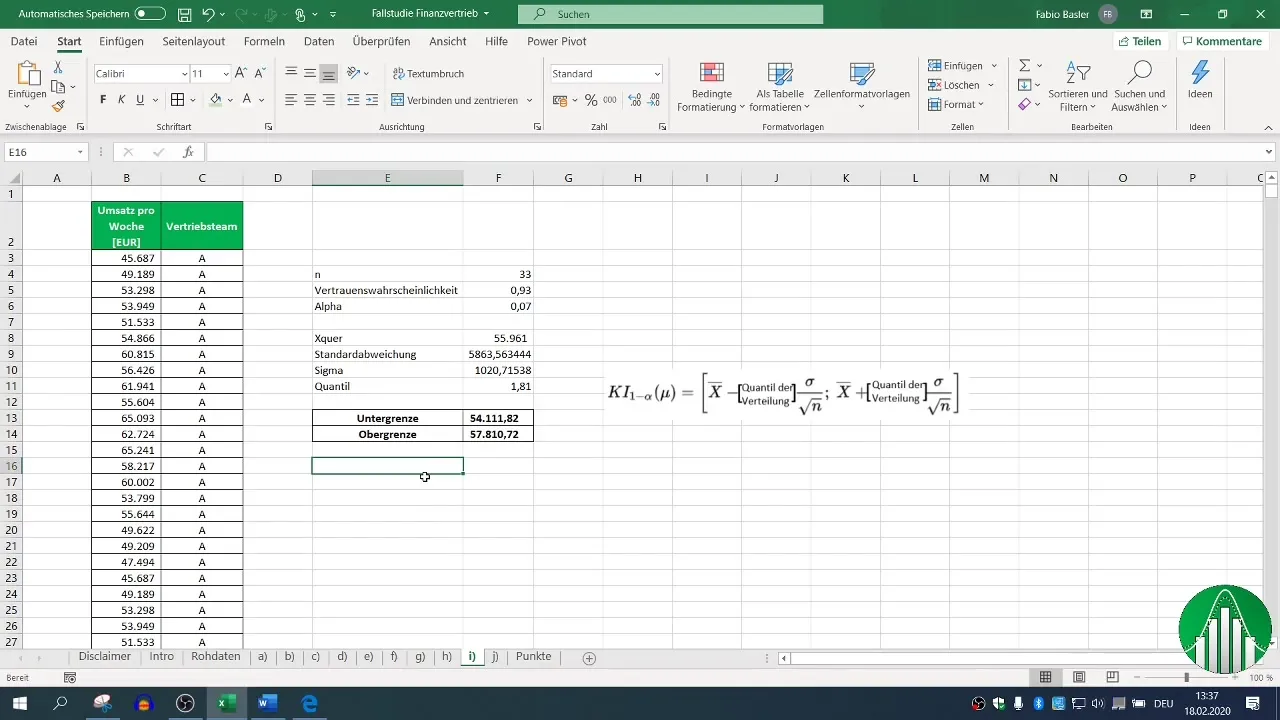
Conclusion
En calculant précisément l'intervalle de confiance bilatéral, tu peux faire des déclarations précises sur le chiffre d'affaires futur. Tu as appris comment préparer les données pertinentes, calculer la moyenne et l'écart-type, et finalement déterminer les limites de l'intervalle. Cette méthode te permet de prendre des décisions basées sur les données dans ton domaine de vente.
Questions fréquemment posées
Qu'est-ce qu'un intervalle de confiance bilatéral ?C'est un intervalle qui inclut l'estimation d'une valeur de paramètre avec une certaine probabilité.
Que faire si je n'ai pas de distribution normale ?Si la distribution normale n'est pas présente, vous pouvez également utiliser toute hypothèse de distribution.
Pourquoi le quantile est-il important ?Le quantile vous aide à déterminer les intervalles pour la limite supérieure et inférieure de l'intervalle de confiance.


