La capacité d'utiliser des outils d'analyse de données dans Excel est cruciale pour le succès en affaires et en vente. Le guide présent se concentre sur l'analyse de la corrélation et de la régression pour déterminer comment le nombre d'employés et le nombre d'appels téléphoniques influencent les chiffres de vente. La réalisation des deux analyses t'aidera à évaluer ces relations quantitativement et à rendre l'interprétation des résultats compréhensible.
Principales conclusions
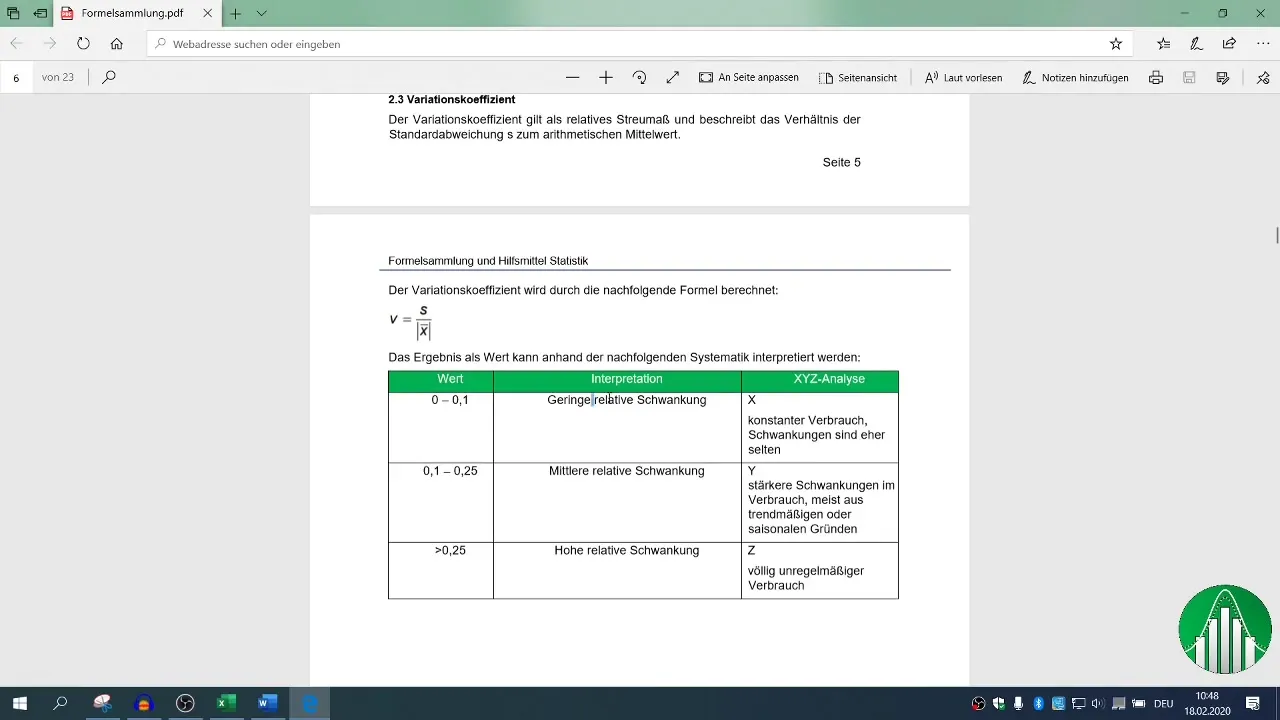
- Différence entre corrélation et régression : la corrélation montre la relation entre deux variables, tandis que la régression étudie l'impact de plusieurs variables indépendantes sur une variable dépendante.
- Compréhension de la signification statistique et de la qualité du modèle.
- Évaluation quantitative de l'importance des régresseurs.
Guide étape par étape
1. Préparatifs pour l'analyse des données
Avant de commencer l'analyse, assure-toi que tes données sont correctement préparées dans Excel. Importe les données sur les ventes, le nombre d'employés et les appels téléphoniques dans une feuille de calcul Excel. Vérifie que toutes les données sont complètes et que les variables nécessaires sont présentes.

2. Réalisation de l'analyse de corrélation
Pour analyser la corrélation entre les variables de vente, d'employés et d'appels téléphoniques, tu peux calculer le coefficient de corrélation. Pour cela, utilise la formule =CORREL() dans Excel. Pour obtenir un aperçu de toutes les variables, crée une matrice de corrélation.
Sélectionne d'abord les colonnes correspondantes pour les ventes et le nombre d'employés. Avec la formule =CORREL() tu marques les zones pour les ventes et le nombre d'employés. Le résultat montre l'intensité de la relation.
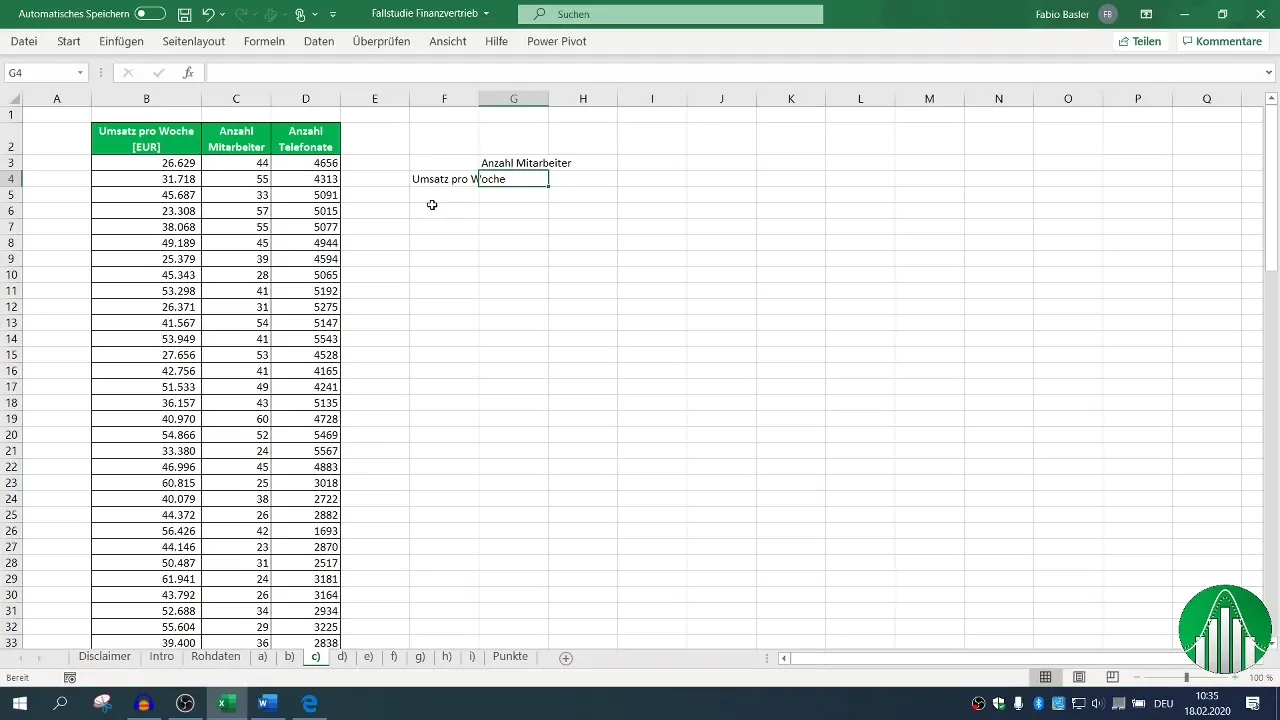
3. Création d'une matrice de corrélation
Pour une analyse plus approfondie, il est recommandé d'utiliser les fonctions d'analyse de données d'Excel. Active la fonction d'analyse de données si ce n'est pas déjà fait. Va sur l'onglet « Données », clique sur « Analyse de données » et sélectionne « Corrélation ».
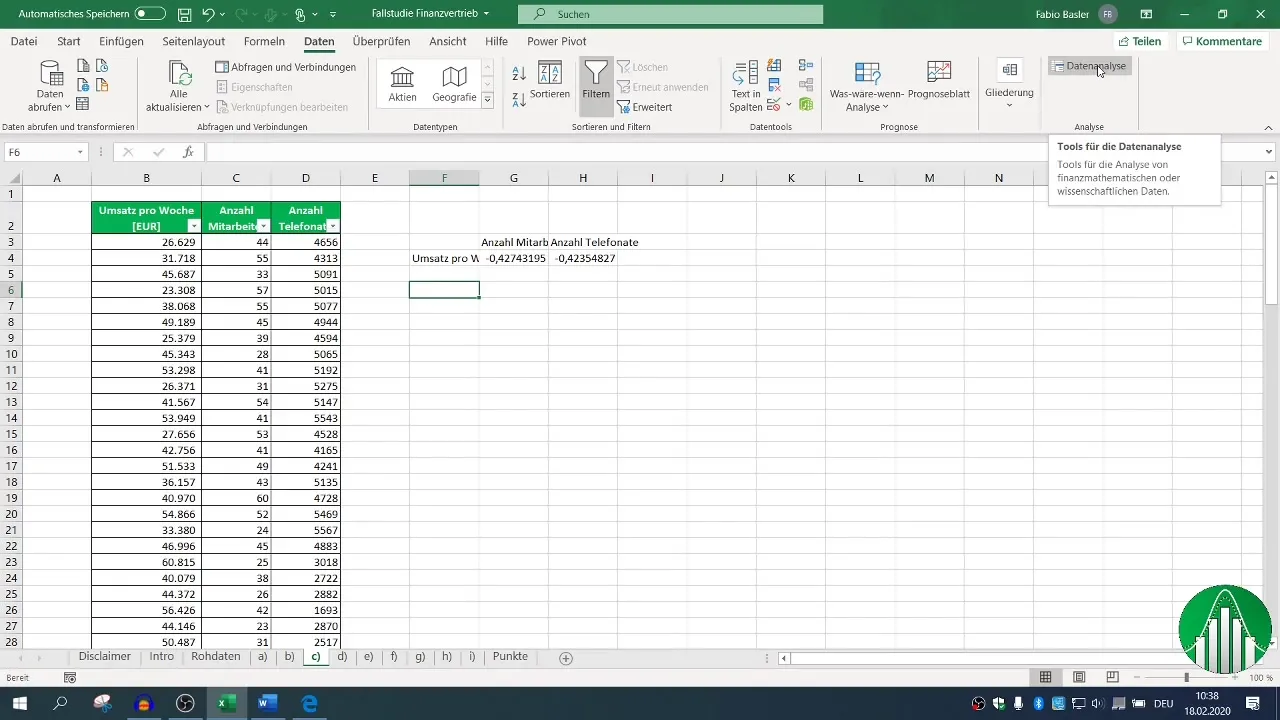
Définis la plage d'entrée de tes données et coche la case pour les en-têtes, pour que Excel reconnaisse correctement les libellés. Après avoir défini la plage de sortie, tu peux générer la matrice de corrélation qui te montrera toutes les relations pertinentes.
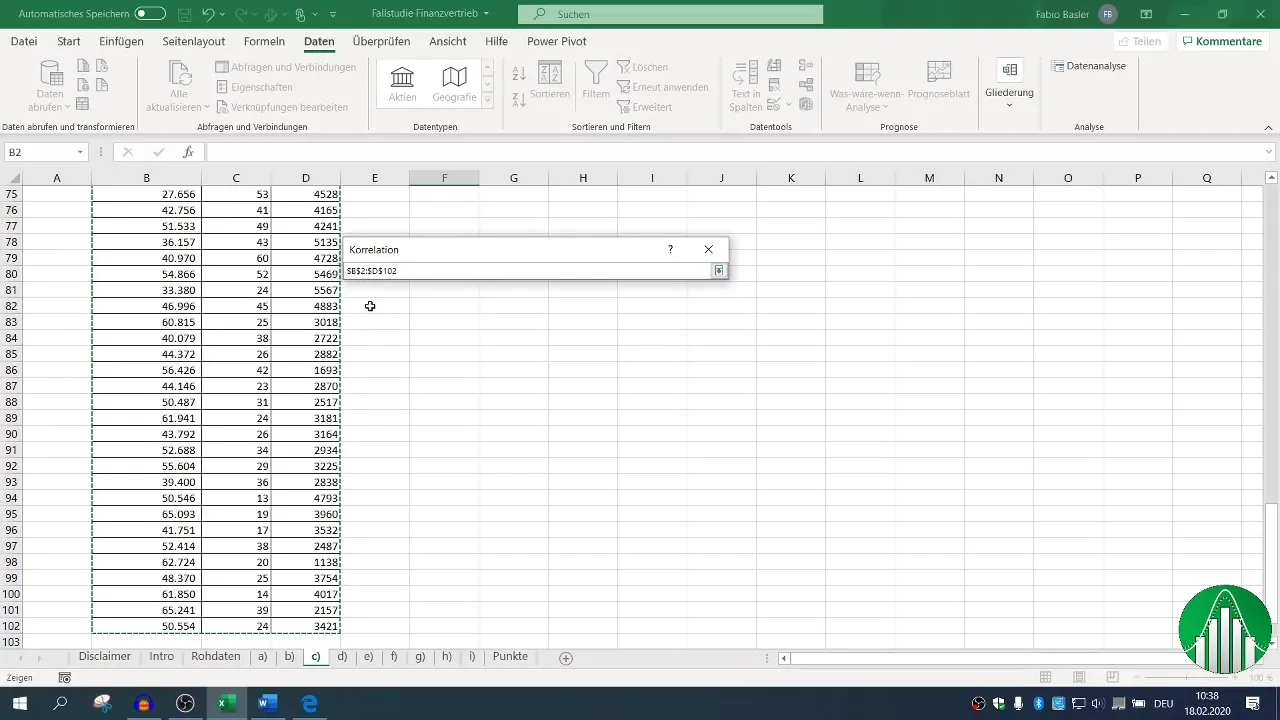
4. Visualisation des corrélations
Pour rendre les résultats plus visuels, un diagramme XY peut être utile. Sélectionne tes données X et Y et génére le nuage de points.
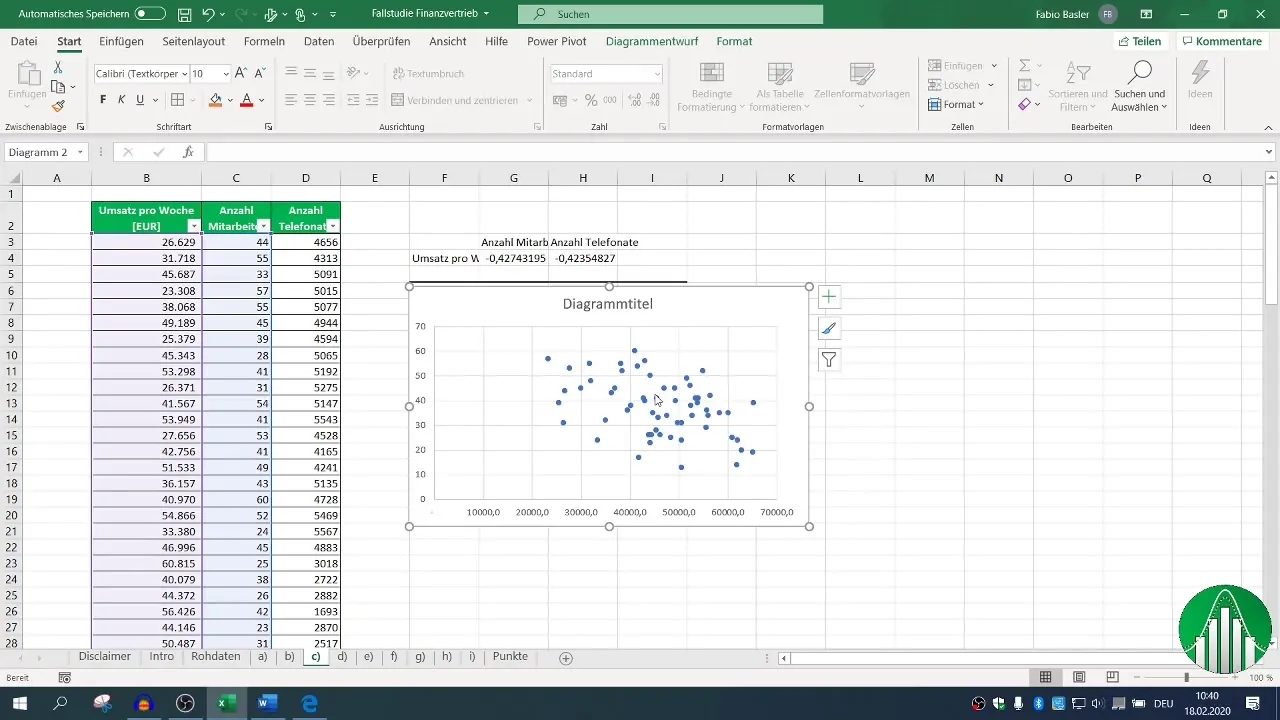
Ajoute une ligne de tendance pour visualiser la relation. Cela peut offrir un aperçu plus intuitif des données.
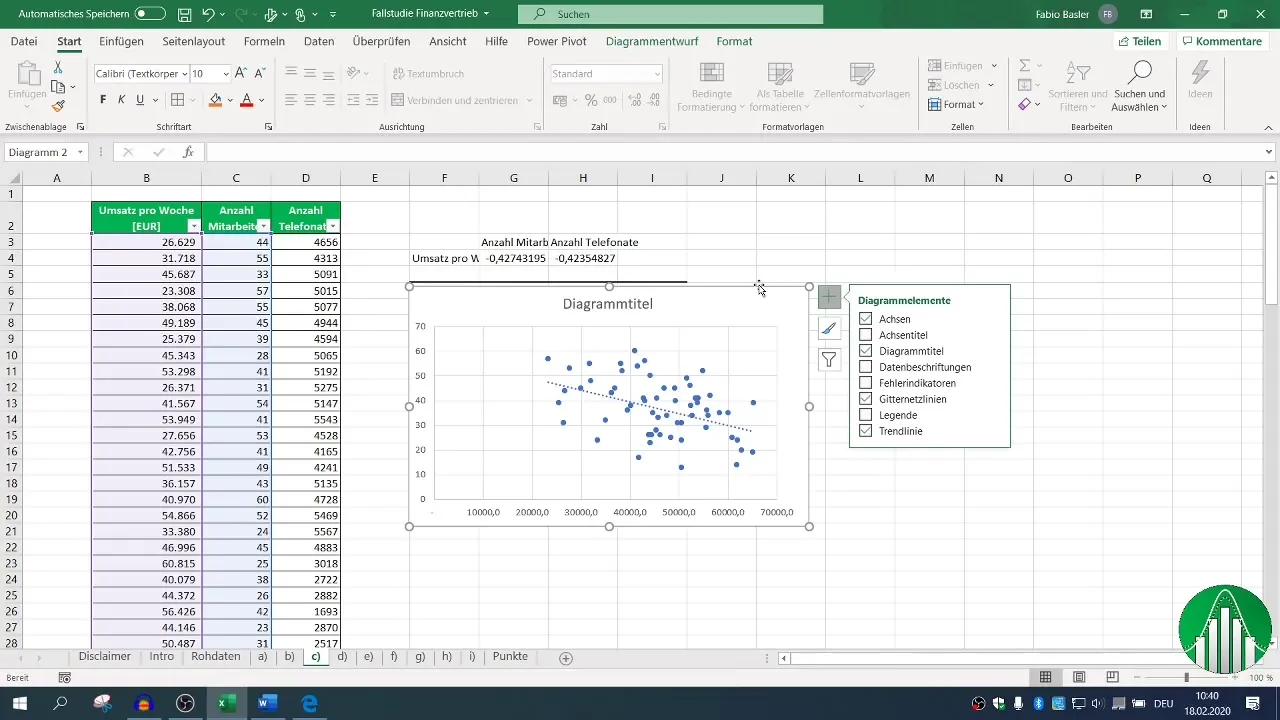
5. Réalisation de l'analyse de régression
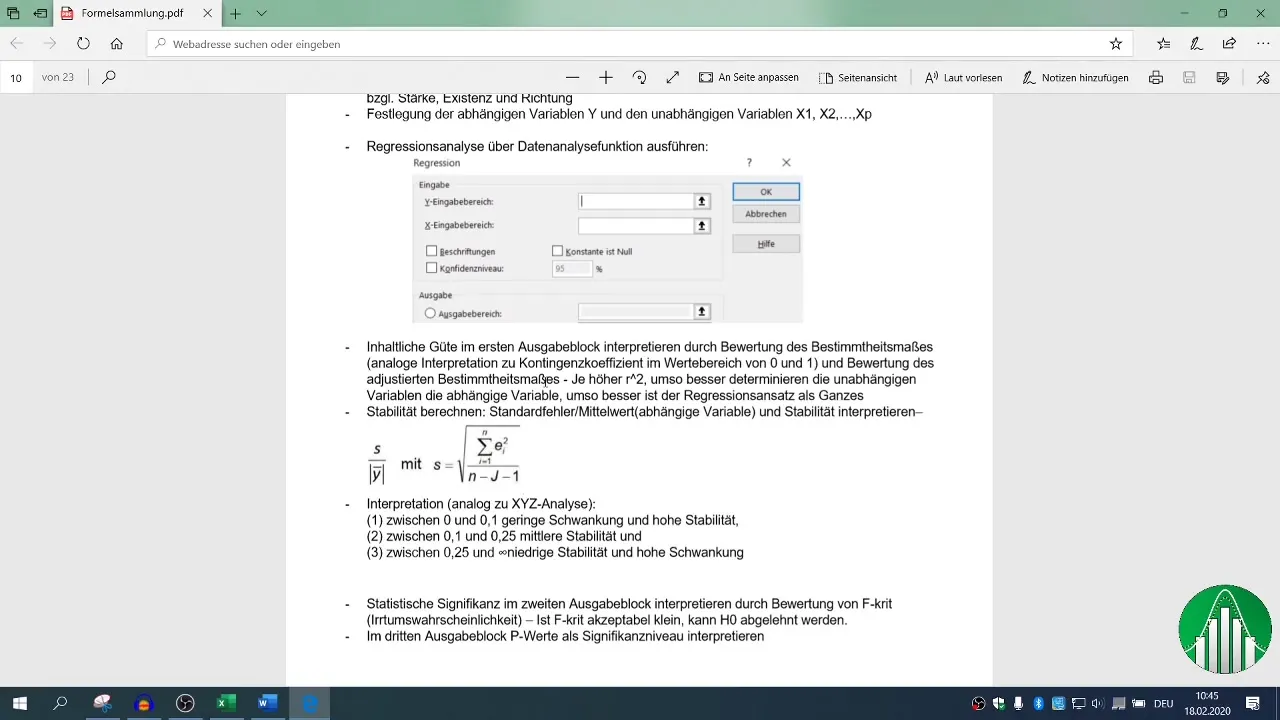
Ensuite, procède à l'analyse de régression. Retourne à « Données » et sélectionne « Analyse de données », puis « Régression ». Ici, définis pour la plage d'entrée la variable dépendante (ventes) et les variables indépendantes (nombre d'employés et appels téléphoniques).
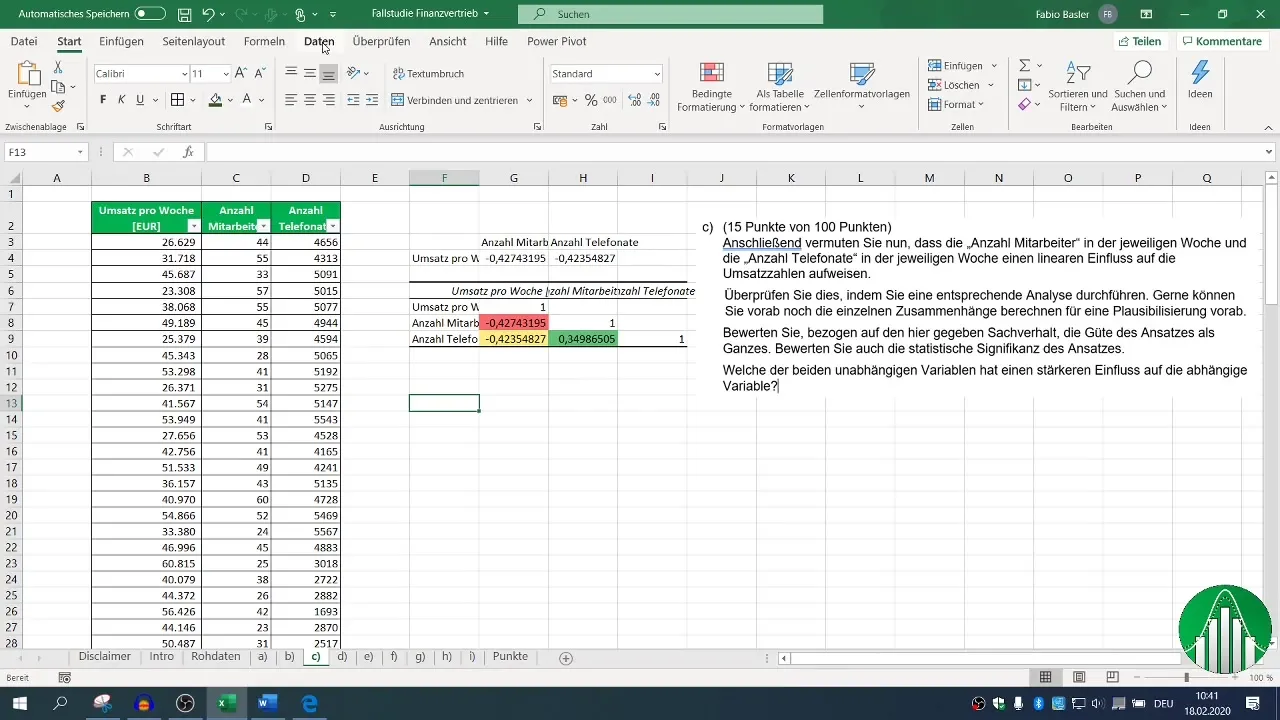
Assure-toi que l'en-tête est défini pour les valeurs et définis ta plage de sortie. Le niveau de confiance par défaut est fixé à 95 %, ce qui est assez pour la plupart des analyses.
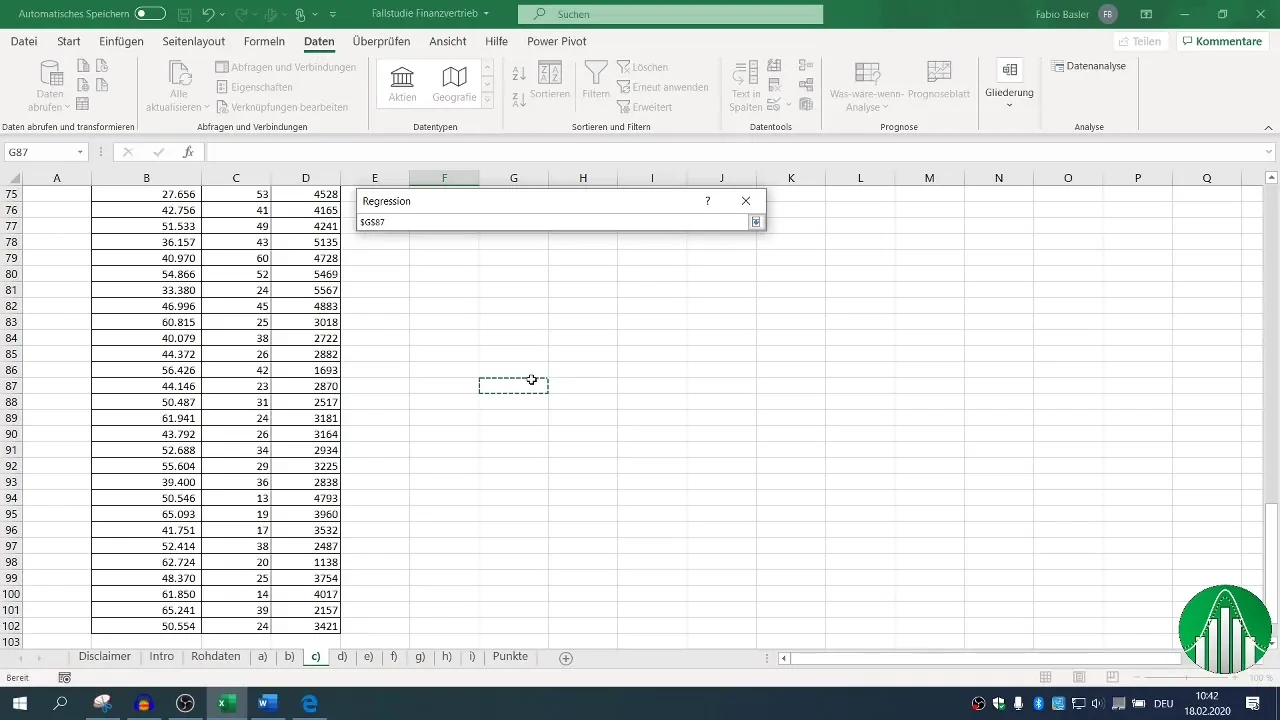
6. Évaluation de l'analyse de régression
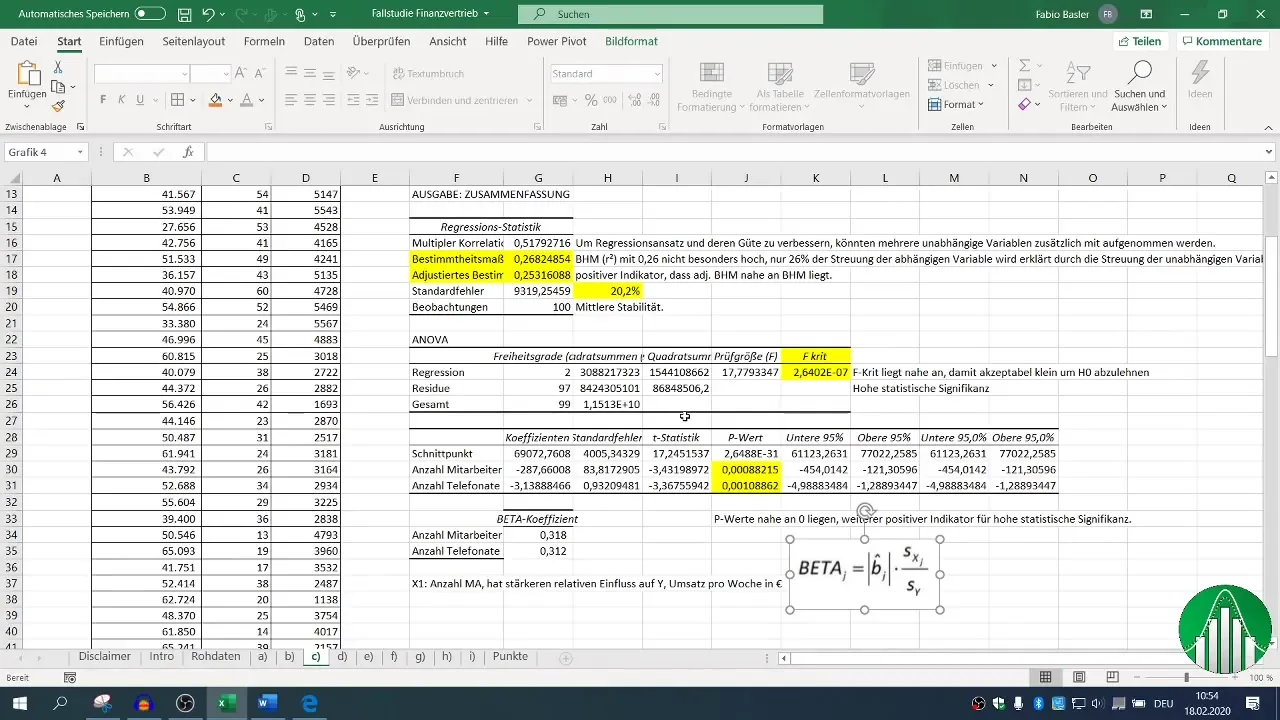
Après avoir effectué la régression, divers blocs de résultats sont disponibles. Concentre-toi sur le coefficient de détermination (R²), qui décrit la qualité du modèle. Un R² de 0,26 indique que seuls 26 % de la variabilité des ventes sont expliqués par les variables indépendantes.
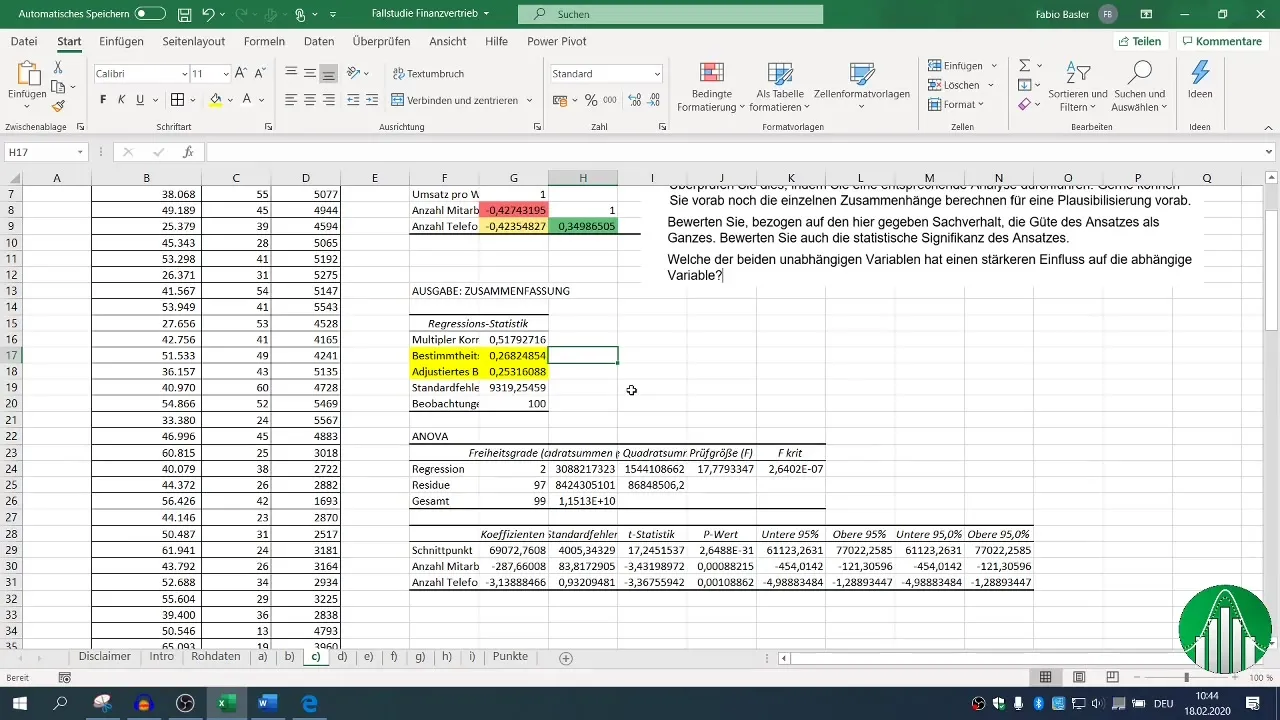
Le coefficient de détermination ajusté devrait être proche de R², ce qui est un indicateur positif dans ce cas.
7. Évaluer la signification statistique
La valeur F et les p-valeurs des variables indépendantes sont essentielles pour évaluer la signification statistique de votre modèle. Une p-valeur inférieure à 0,05 indique que la relation est statistiquement significative.
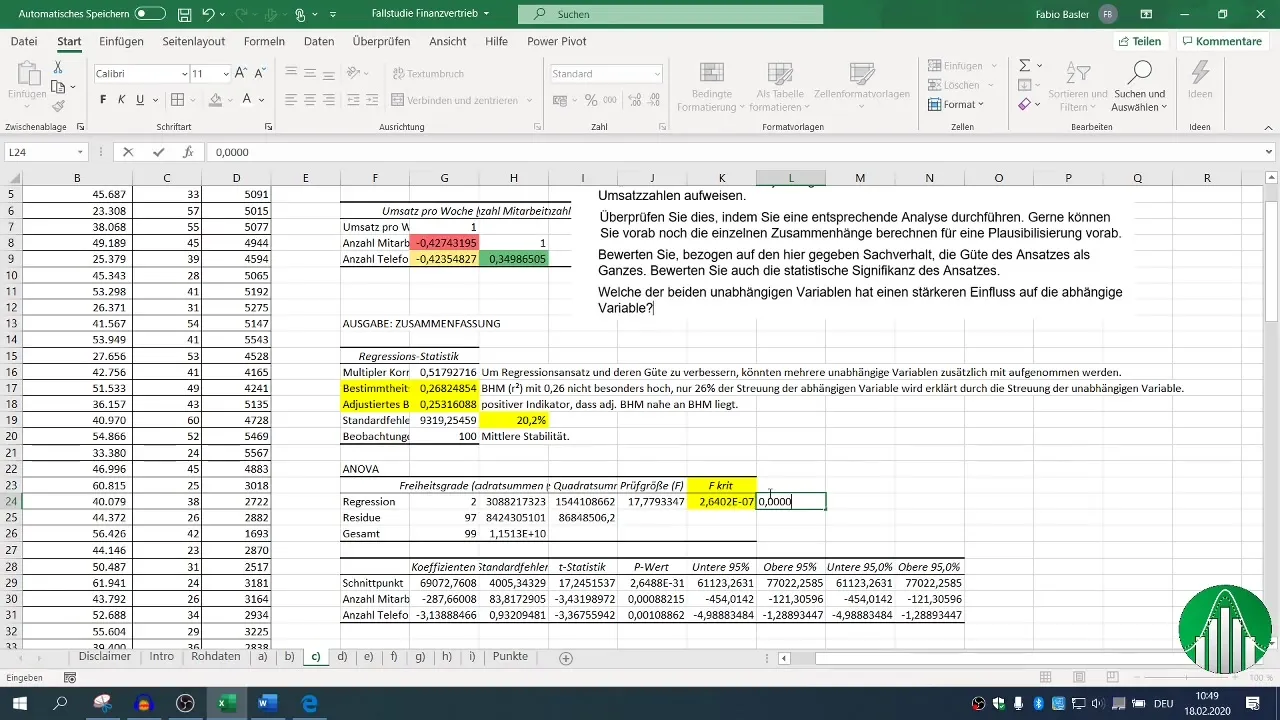
Évaluer ces mesures statistiques en relation avec R² vous aidera à comprendre la stabilité et la portée de vos résultats.
8. Comparaison des facteurs d'influence
En fin de compte, vous voulez savoir quel facteur - nombre d'employés ou d'appels téléphoniques - a une influence plus forte sur les chiffres d'affaires. Vous prendrez alors les coefficients bêta en main pour les comparer.
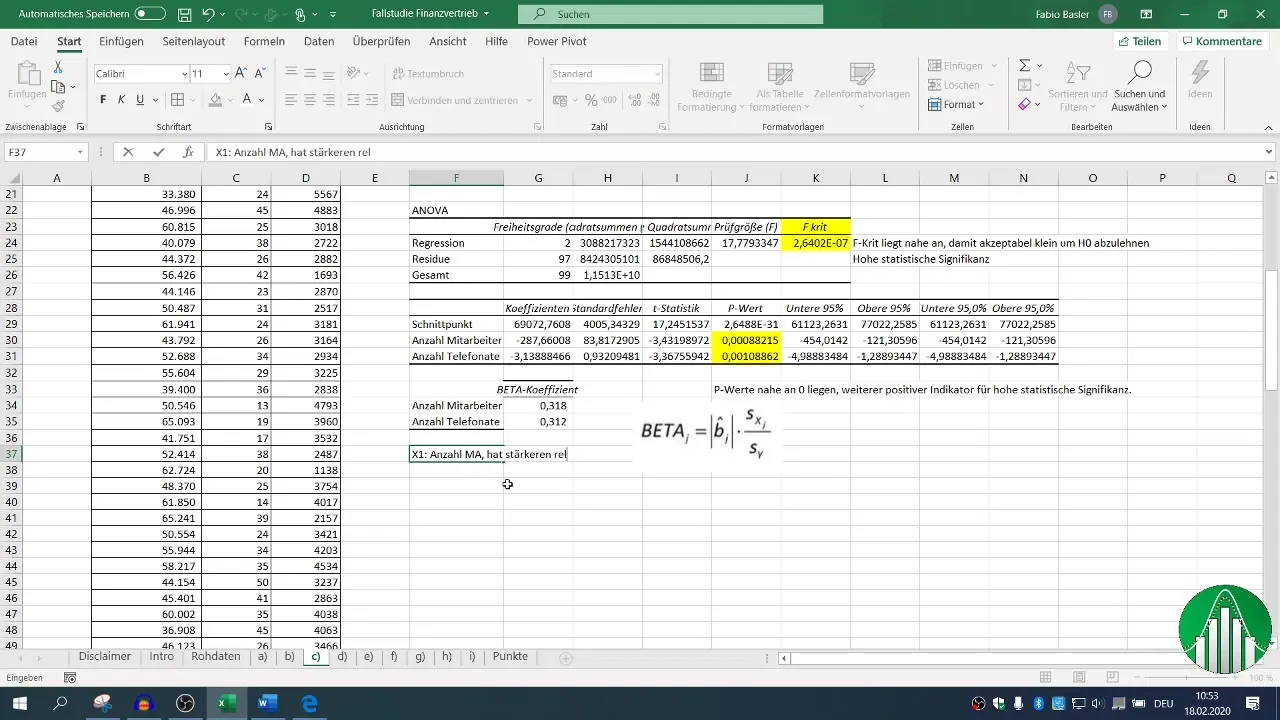
Un coefficient bêta plus élevé indique l'influence relative ; il est possible que le nombre d'employés ait une plus grande influence sur les revenus que le nombre d'appels téléphoniques.
Résumé
L'analyse précédente vous a apporté des informations précieuses sur les relations statistiques entre les variables de chiffre d'affaires, le nombre d'employés et les appels téléphoniques. En effectuant systématiquement des analyses de corrélation et de régression dans Excel, vous pourrez prendre des décisions éclairées basées sur vos résultats.
Questions fréquemment posées
Pourquoi une analyse de corrélation est-elle importante ?Une analyse de corrélation aide à identifier la relation entre deux variables avant d'effectuer une analyse de régression détaillée.
Comment interpréter R² dans une analyse de régression ?Un R² de 0,26 signifie que 26 % des variations de la variable dépendante (chiffre d'affaires) sont expliquées par les variables indépendantes.
Quelle est la différence entre corrélation et régression ?La corrélation mesure la relation entre deux variables, tandis que la régression évalue l'impact de plusieurs variables indépendantes sur une variable dépendante.
Comment tester la signification statistique ?Vous testez la signification statistique en utilisant la valeur p ; les valeurs p inférieures à 0,05 sont considérées comme significatives.
Quel est le rôle des coefficients bêta ?Les coefficients bêta indiquent l'influence relative des variables indépendantes sur la variable dépendante.


