Les analyses de corrélation de rang sont d'une importance centrale dans l'étude statistique des relations entre variables. En particulier, lorsqu'il s'agit de données ordinales, la corrélation de rang de Spearman est une méthode précieuse pour détecter des motifs et des liens. Dans ce guide, vous apprendrez étape par étape comment calculer la corrélation de rang selon Spearman pour une enquête à l'aide d' Excel.
Principales conclusions
- La corrélation de rang mesure la force et la direction d'une relation monotone entre deux variables ordinales.
- Le coefficient de corrélation de rang de Spearman est particulièrement adapté lorsque l'une des variables est ordonnée et l'autre est scalaire.
- Le calcul dans Excel peut être effectué à l'aide de formules et fonctions simples.
Guide étape par étape
Nous commençons par définir les variables que nous voulons analyser. Dans ce cas, il s'agit de la satisfaction des clients (classée par ordre, valeurs de 1 à 3) et du nombre de commandes (classé par métrique).
Pour établir une classification pour la satisfaction et le nombre de commandes, vous aurez besoin d'un tableau contenant les données adéquates. Assurez-vous de saisir ces données dans Excel.

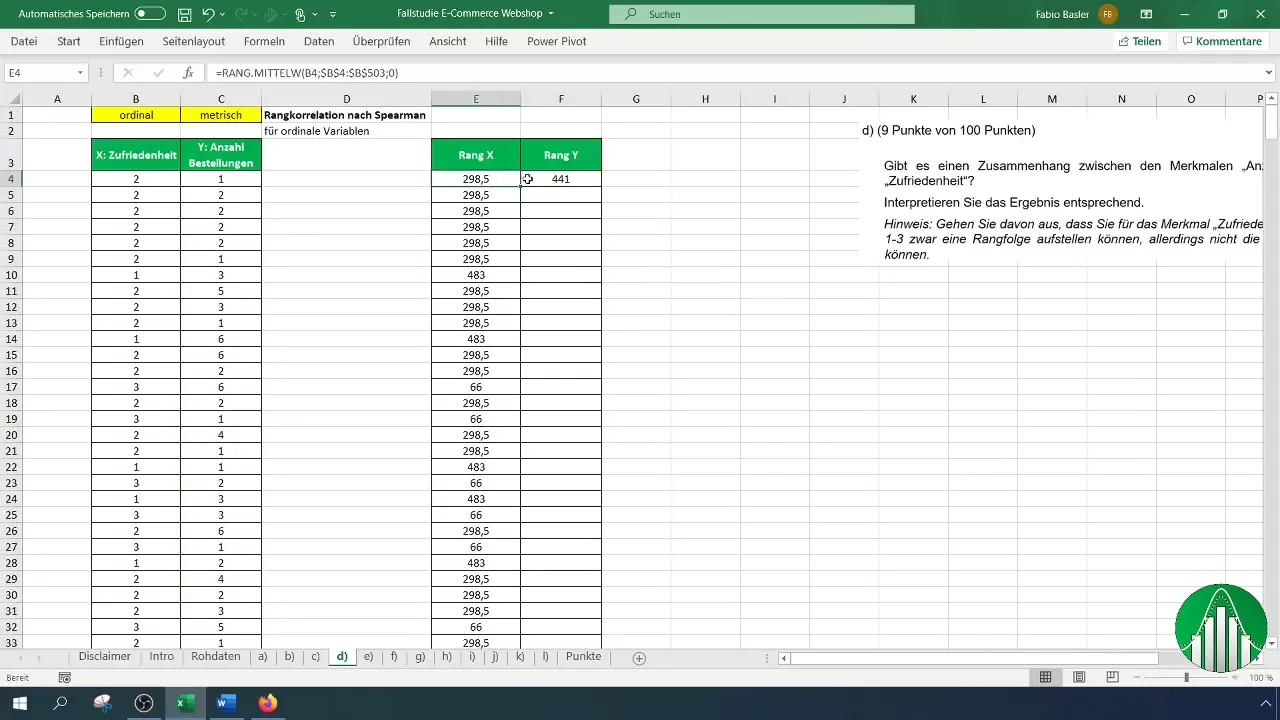
Après avoir entré vos données dans Excel, nous examinons le calcul de la corrélation de rang selon Spearman. Pour cela, nous utilisons la fonction « RANG.MOYEN » dans Excel, qui renvoie le rang d'un nombre dans une liste. Pour la satisfaction, nous utilisons tout d'abord la formule suivante :
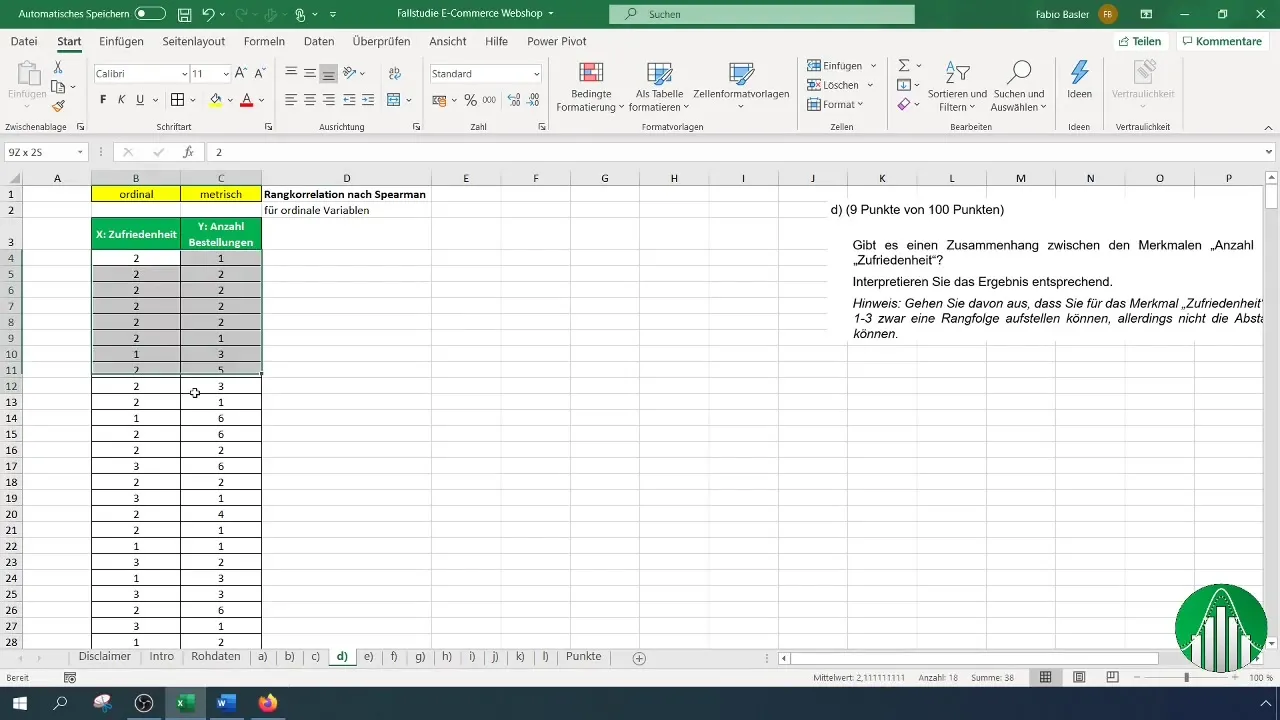
Lors de l'application de cette formule, veillez à sélectionner la colonne pour la satisfaction et à fixer la plage entière de B4 jusqu'à la fin de votre série de données pour identifier correctement les rangs.
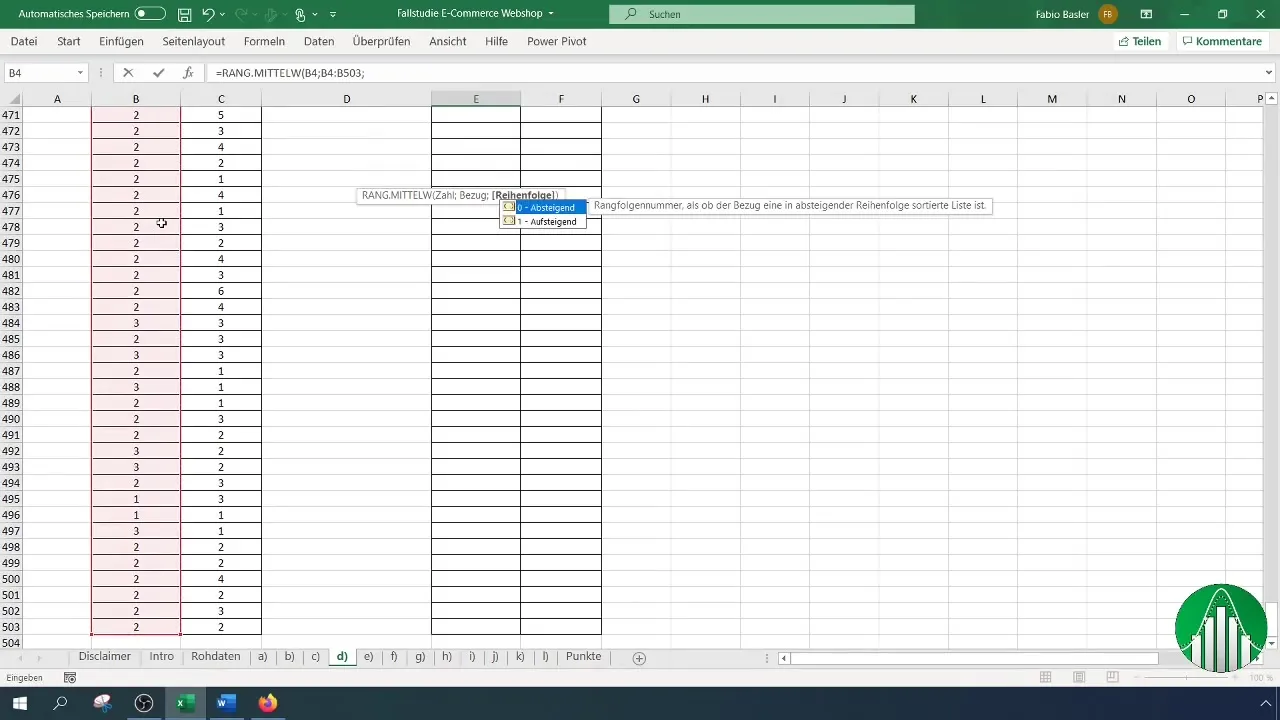
Décidez si vous souhaitez trier les rangs par ordre croissant ou décroissant. En général, il est préférable de les trier par ordre croissant. Soulignez que les références de cellule pour les rangs sont fixées en appuyant sur la touche F4. Ceci est important pour éviter que les références ne soient modifiées lors de la copie.
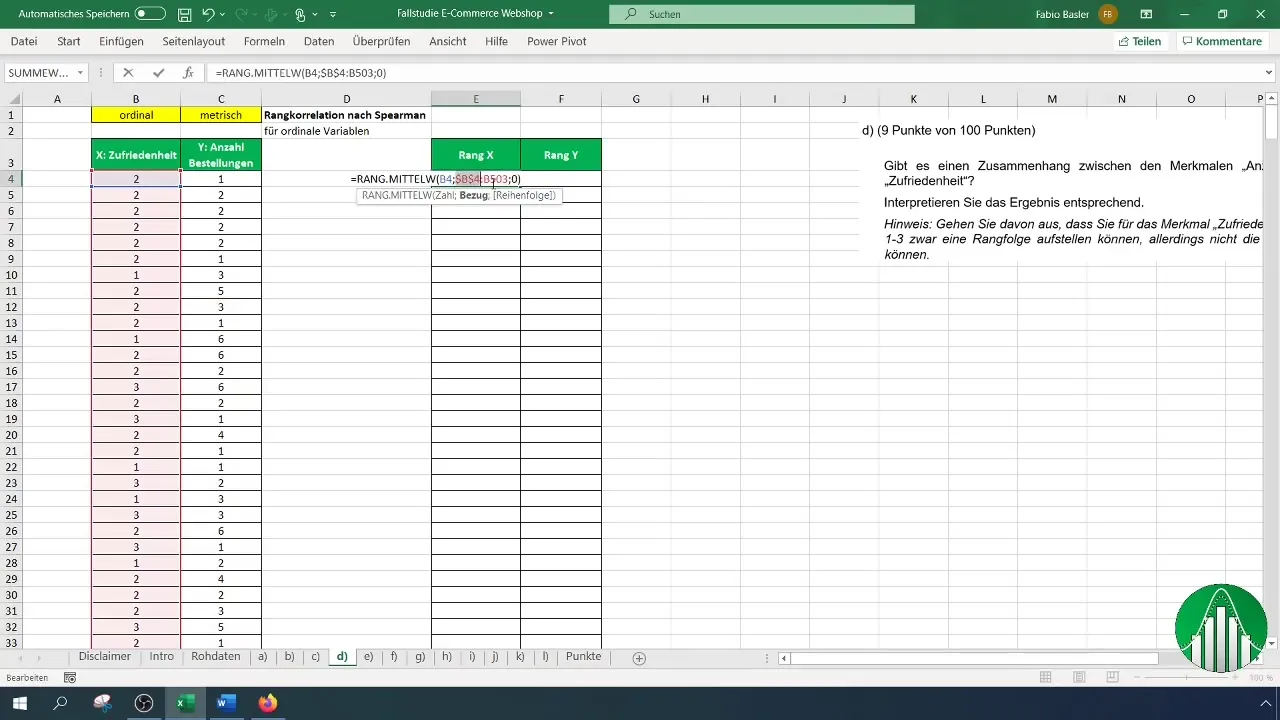
Une fois que vous avez défini les rangs de satisfaction, répétez le processus pour le nombre de commandes. Assurez-vous d'appliquer correctement la formule et la référence.
Avec les deux listes de rangs (satisfaction et nombre de commandes), vous êtes prêt à calculer le coefficient de corrélation de rang selon Spearman. Pour ce faire, utilisez la formule « =CORREL » pour déterminer la relation. La syntaxe est la suivante :
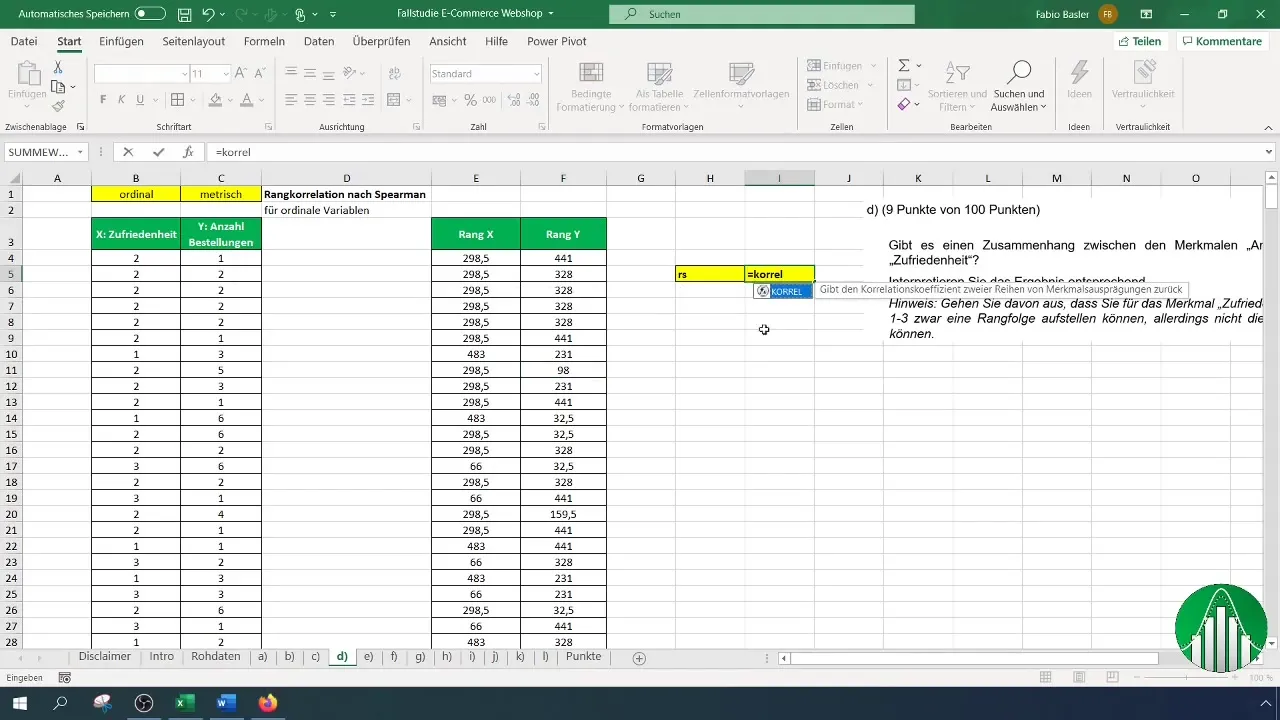
Indiquez la liste de rangs de satisfaction pour la première référence et la liste de rangs des commandes pour la deuxième référence. Excel calculera automatiquement le coefficient de corrélation de rang de Spearman.

Quel est le résultat de votre calcul ? Une valeur de 5,61 % indique une faible corrélation positive entre la satisfaction et le nombre de commandes. Cela signifie qu'il y a peu de relation significative entre ces deux variables.
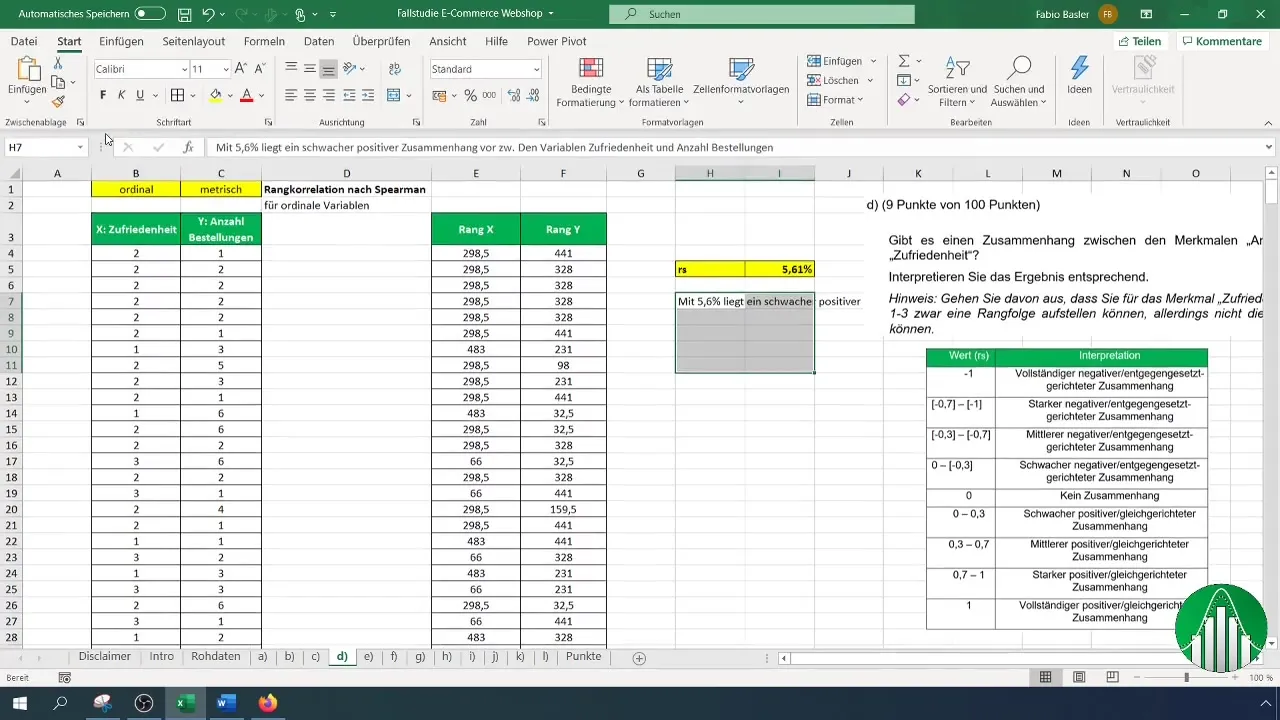
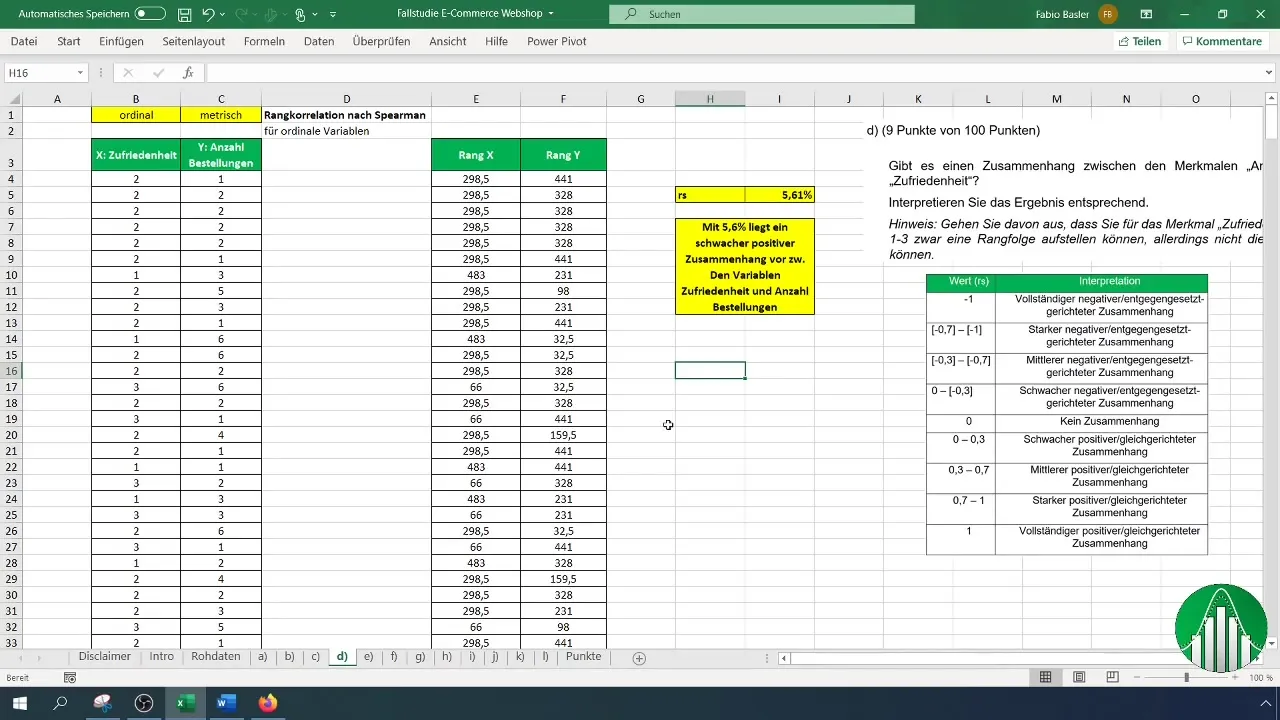
Pour interpréter vos résultats, utilisez un tableau de valeurs répertoriant les différents domaines de la corrélation de rang. Après l'interprétation, nous confirmons que le faible taux de corrélation signifie que les variables sont relativement indépendantes.
Résumé
Effectuer une analyse de corrélation de rang selon Spearman dans Excel vous permet d'obtenir des informations précieuses sur les relations entre les variables ordinales et métriques. La méthode est facile à appliquer et offre une vue claire sur d'éventuelles relations.
Questions fréquemment posées
Que signifie le coefficient de corrélation de rang de Spearman ?Le coefficient de corrélation de rang de Spearman mesure la force et la direction d'une relation monotone entre deux variables.
Quand est-il judicieux d'utiliser le coefficient de Spearman ?Il est judicieux de l'utiliser lorsque au moins l'une des variables est ordinalement échelonnée.
Comment calculer le coefficient de Spearman dans Excel ?Utilisez la fonction « Rang.Mittel » pour déterminer les rangs, puis la fonction « KORREL » pour calculer la corrélation.
Quel est l'intervalle de valeurs du coefficient de Spearman ?Le coefficient est compris entre -1 et 1. Les valeurs proches de 1 indiquent une forte corrélation positive, tandis que les valeurs proches de -1 indiquent une forte corrélation négative.
Que peut signifier une valeur de 5,61 % dans la corrélation des rangs ?Une valeur de 5,61 % indique une faible corrélation positive, suggérant que les variables sont relativement indépendantes.


