Az összefüggések elemzése egy alapvető készség, amely elengedhetetlen számos tudományos és üzleti területen. Az Excel segítségével meghatározhatod a Pearson-korrelációs együtthatót, hogy a változók közötti kapcsolatokat mennyiségi módon mérhesd. Ebben az útmutatóban lépésről lépésre megmutatom, hogyan végezhetsz korrelációs elemzést az okostelefonok és notebookok forgalmának Excelben.
Legfontosabb megállapítások
- A Pearson-korrelációs együttható mennyiségi értékelést nyújt két változó közötti kapcsolat tekintetében.
- Tájékozódj a különböző módszerekről az Excelben a korrelációs együttható számítására.
- Az eredmények vizualizációjával diagramok segítségével könnyebben megérthetővé válnak a változók közötti kapcsolatok.
Lépésről lépésre útmutató
A következő eljárás megmutatja, hogyan számíthatod ki a Pearson-korrelációs együtthatót az Excelben. Arra összpontosítunk, hogy az okostelefonok és notebookok forgalmáról egyértelmű és gyakorlatias alkalmazást mutassunk.
A korrelációs elemzés megkezdéséhez először nyiss meg egy új Excel munkafüzetet, vagy használj egy meglévőt, amely tartalmazza a releváns adatokat.

Először győződj meg arról, hogy az okostelefonok és notebookok releváns forgalma két külön oszlopban van megadva. Ezek az oszlopok képezik az elemzés alapját. Ügyelj rá, hogy az adatok teljesek és helyesek legyenek, hogy elkerüld a torzított eredményeket.
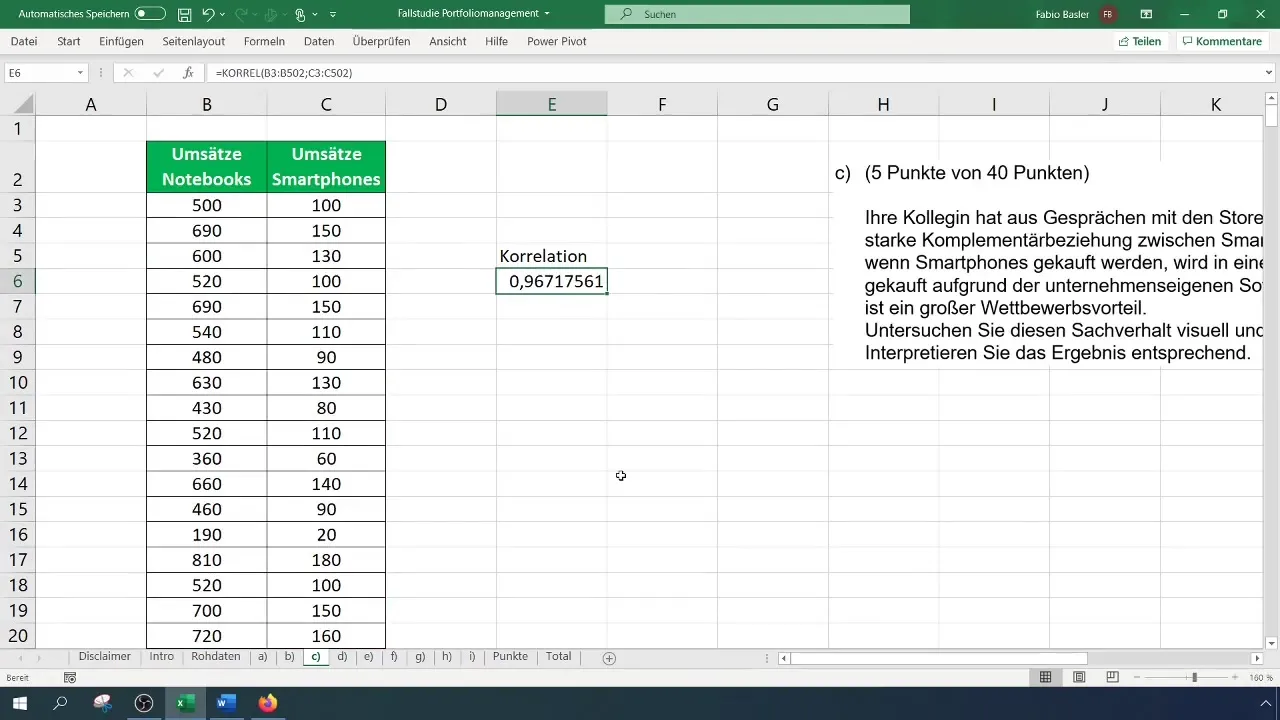
Miután megadtad az adatokat, jelöld ki a két forgalommal rendelkező oszlopot. A korrelációs együttható kiszámításához írd be egy üres cellába a =KORREL() képletet, majd a két adatmezőt. Ez a függvény kiszámítja a Pearson-korrelációs együtthatót a kiválasztott adatok alapján.
Ha a =KORREL(Tartomány1; Tartomány2) képletet alkalmazod, válaszd ki az oszlop teljes tartományát, amely a notebook-forgalmat jelenti, majd az okostelefon-forgalom tartományát. Az eredmény megmutatja neked a változók közti korrelációt. Egy magas korreláció esetén, pl. 0,96, ez egy erős pozitív kapcsolatra utal.
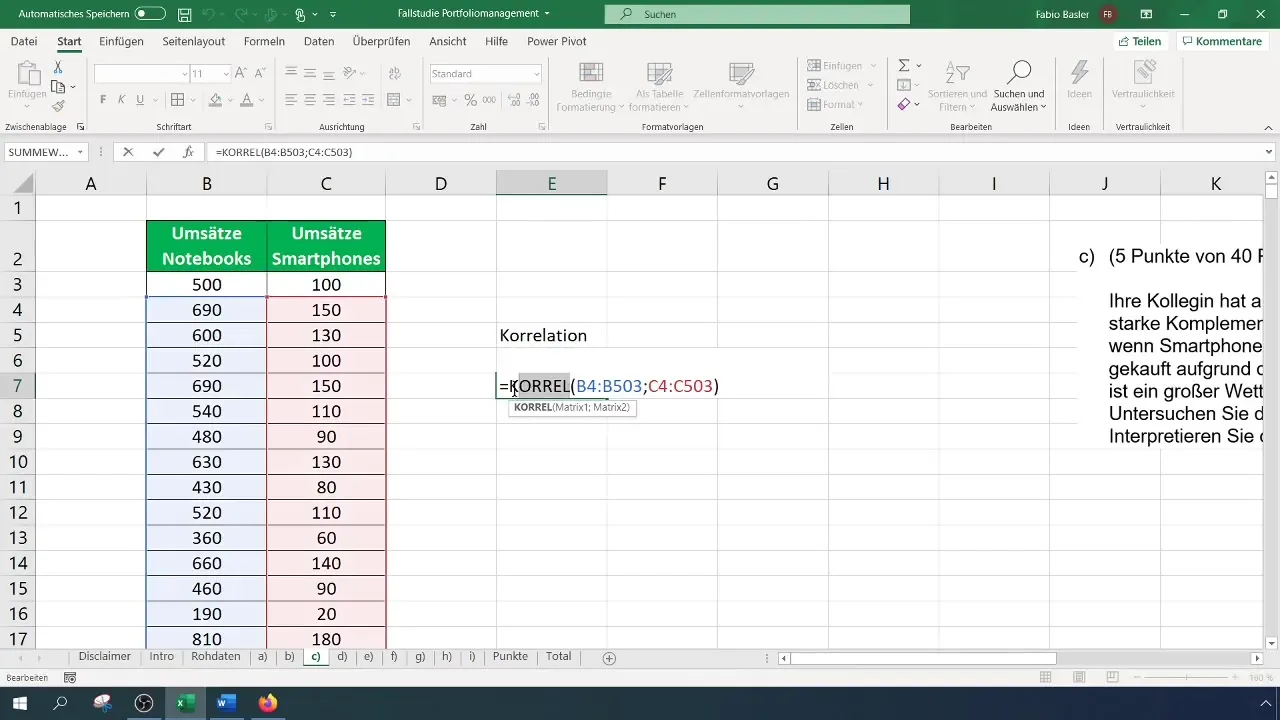
A KORREL-függvény mellett használhatod a =PEARSON() függvényt, amely azonos eredményt ad. Használd ezt a függvényt hasonlóan az előbbihez, és válaszd ki az adatmezőket a korreláció kiszámításához.
Az Excelben rendelkezésre álló korrelációs elemzés további érdekes lehetőséget kínál. Az aktiváláshoz menj az „Fájl” menüpontra, majd „Beállítások”. Az „Ad-ins” pont alatt engedélyezheted a „Datanalízis” lehetőséget, ha még nem aktiváltad.
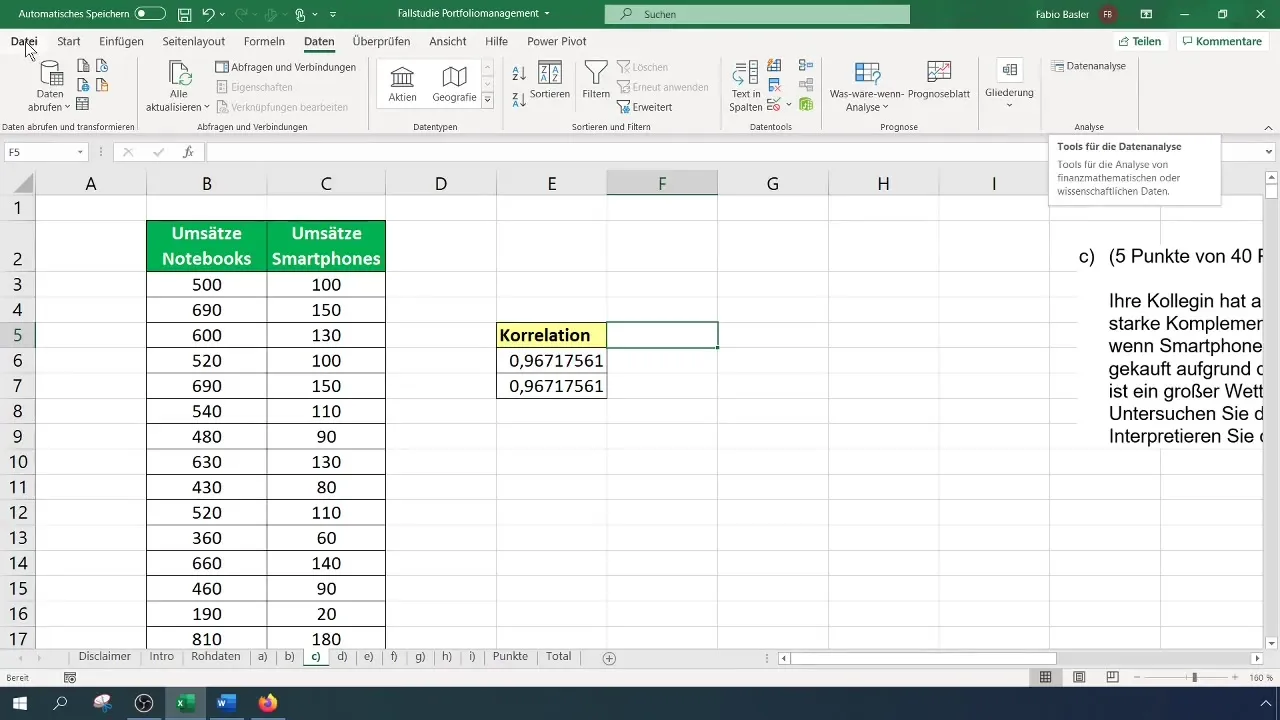
A Datanalízis funkció aktiválása után a „Datanalízis” lehetőséget válaszd a menüszalagról, majd kattints a „Korreláció” lehetőségre. Egy bevitelelmező fog megnyílni, ahova be tudod állítani bemeneti adatok tartományát a szöveges fejlécekkel együtt.
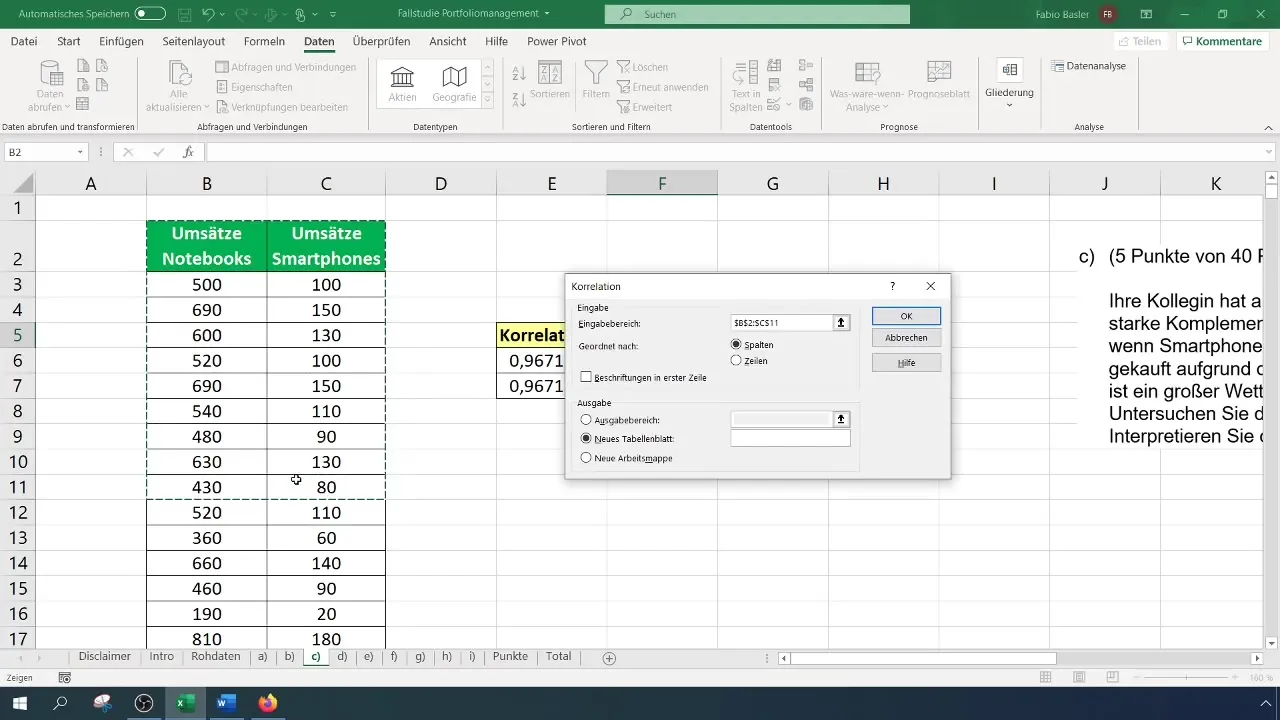
A kimeneti tartomány megadásakor válassz egy üres cellát, amelyben az eredmények meg fognak jelenni. A beküldés megerősítése után egy korrelációs mátrix generálódik, amely megmutatja az összes kapcsolatot a megadott adatok között. Itt ismét a magas, pl. 0,96-os korrelációt fogod észlelni.
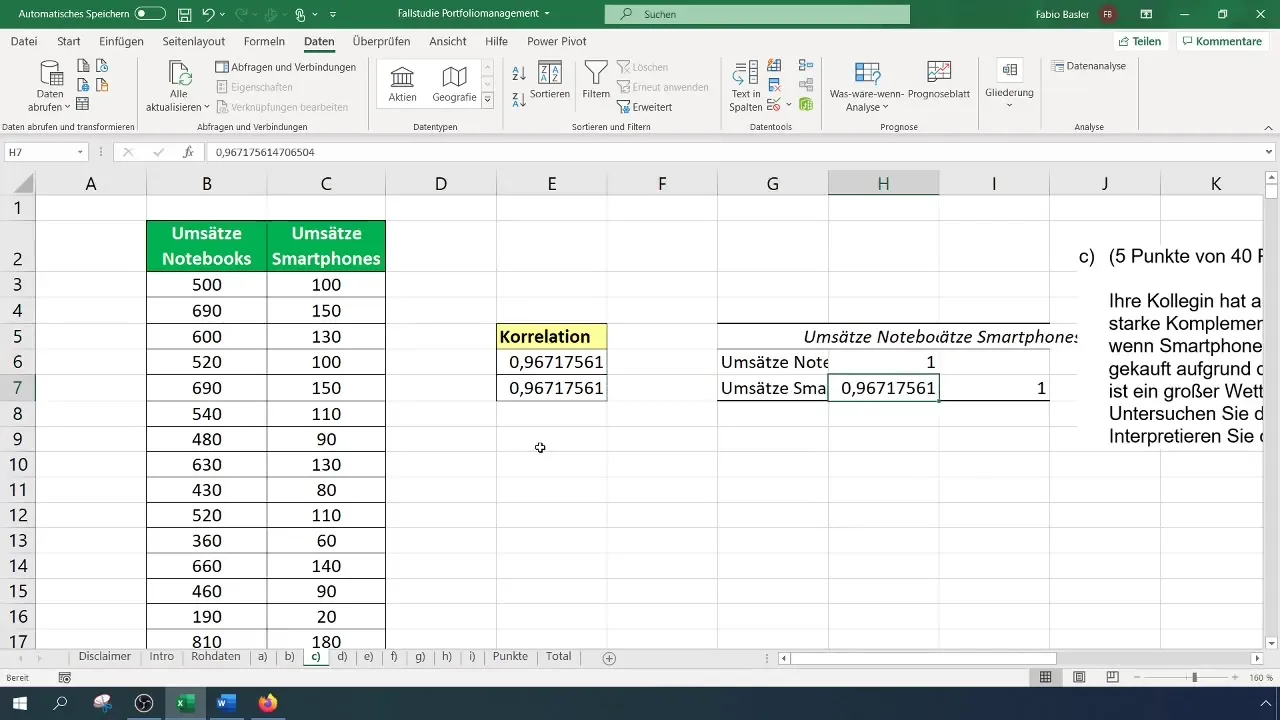
A változók közötti kapcsolatot vizuálisan ábrázolni egy pontdiagram segítségével lehetséges. Ehhez válassz egy üres cellát, majd szúrj be egy XY diagramot. Jobb gombbal kattints a diagramon, majd válaszd a „Adatok kiválasztása” lehetőséget.
Add hozzá az okostelefon és notebook forgalmát. Ez a vizuális ábrázolás megmutatja neked, hogy hogyan vannak elosztva a pontok a két változó között, és érzékelteti az összefüggést a csoportosulási hatások által.
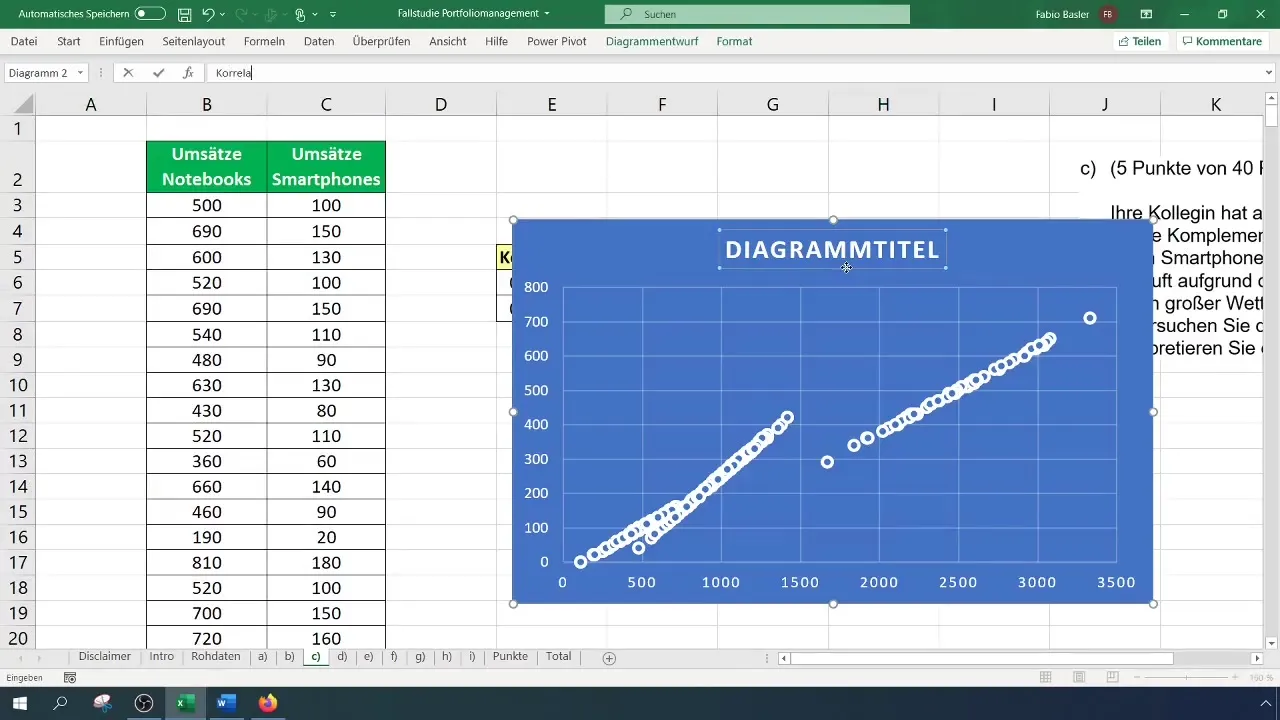
A változók közötti kapcsolat további elemzésének egy lehetősége a trendvonal hozzáadása a diagramhoz. Kattints a diagram jobb felső sarkában található plusz jelre, majd activáld a Trendvonal opciót. Emellett megjelenítheted a formulát és a R² meghatározottsági tényezőt további elemzés céljából.
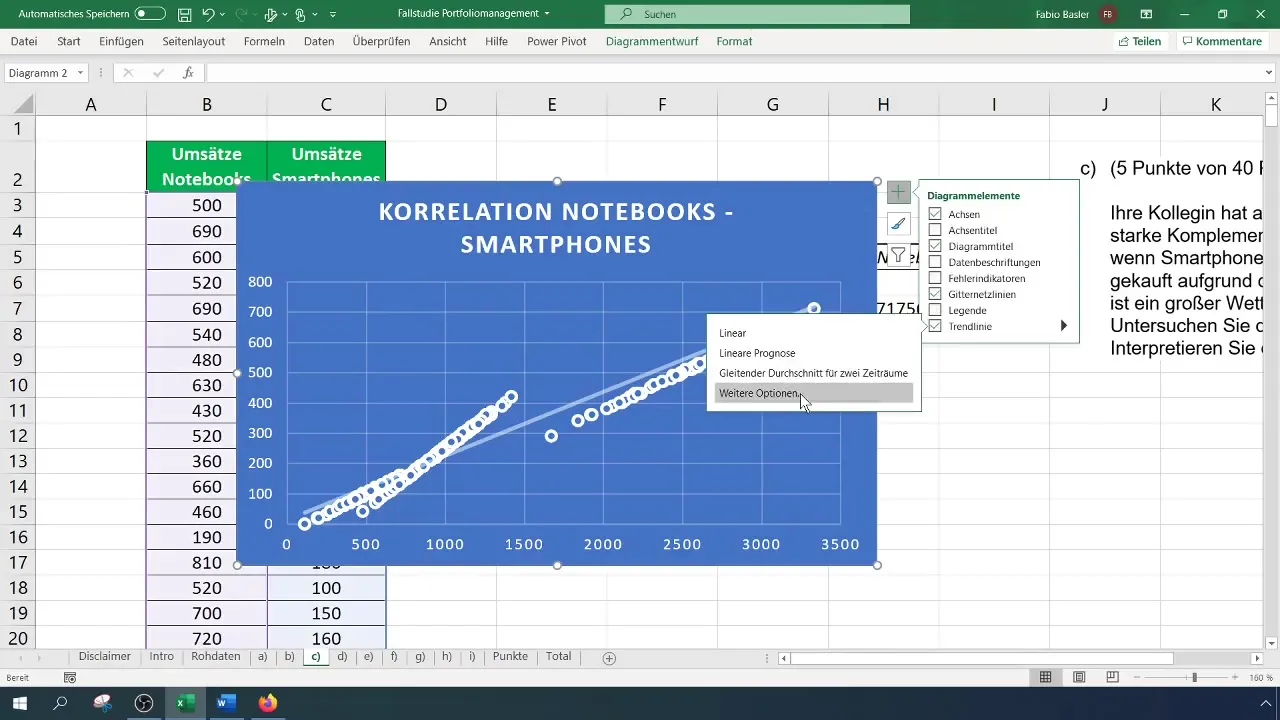
Az meghatározottsági mérték azt jelzi, hogy mennyire jól írja le a trendvonal az adatokat, és a korrelációs együttható négyzete. Az R² körülbelül 0,935 értéke megerősíti a noteszgépek és okostelefonok közötti kapcsolat erősségét, amit az előzőleg számított korreláció is támogat.
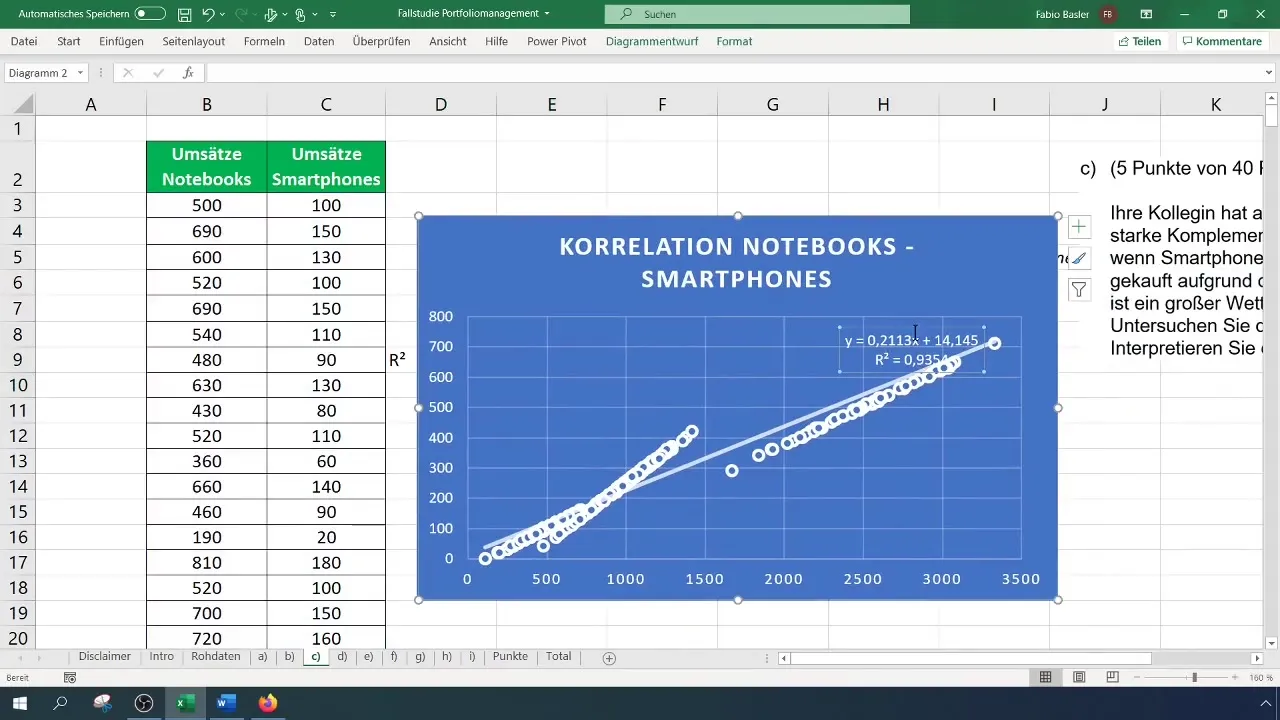
Végül fontos az eredmények értelmezése. Az 0,90 feletti értékek erős pozitív összefüggést mutatnak, ami annyit jelent, hogy a bevételek egy területén bekövetkező növekedés egy másik terület növekedésével jár együtt. Ebben az esetben az okostelefon- és noteszbevétel közt az összefüggés rendkívül erős.
Összefoglalás
Ebben az útmutatóban megtanultad, hogyan számíthatod ki és értelmezheted a Pearson-korrelációt Excelben. A különböző módszerek segítségével többféle módon mutatták be neked, hogyan lehet megjeleníteni a változók közötti korrelációt kvantitatív és vizuális módon. Ezáltal lehetőséged van valódi adatokat elemezni és fontos üzleti megállapításokra jutni.
Gyakran Ismételt Kérdések
Hogyan számolhatom ki a Pearson-korrelációt Excelben?A =KORREL(Tartomány1; Tartomány2) függvényt használhatod a Pearson-korreláció kiszámítására.
Mit jelent a 0,96-os korrelációérték?A 0,96-os korrelációérték erős pozitív kapcsolatot jelent az elemzett változók között.
Hogyan aktiválhatom az adatelemzés funkciót Excelben?Menj az „Fájl” > „Beállítások” > „Kiegészítők”, válaszd ki az „Excel Kiegészítőket”, és jelölj be egy pipát az „Elemzési Funkció” mellett.
Tudom számolni a korrelációs együtthatót mátrix segítségével is?Igen, a „Datanalízis” funkciót használhatod arra, hogy egy több adatsort tartalmazó korrelációs mátrixot hozz létre.
Hogyan értelmezhetem az R² meghatározottsági értéket?Egy R² érték közel 1-hez azt jelzi, hogy a függő változó varianciájának nagy része magyarázható az független változó által.


