A statisztikai tesztek az adatelemzés és a döntéshozatal központi elemei. Különösen a biotechnológia területén lehet döntő fontosságú a hatóanyagok sikerességi arányára vonatkozó hipotézisek tesztelése. Ebben a bemutatóban megtanulhatja, hogyan végezhet hatékonyan egy egymintás tesztet (1-SP teszt ) a várható értékre ismert szórással az Excelben.
A legfontosabb megállapítások
Ez az útmutató megtanítja Önnek:
- Az 1-SP teszt elméleti alapjait.
- A teszt Excelben történő elvégzésének lépéseit.
- Az eredmények értelmezését.
Az adatok előkészítése
Az 1-SP teszt Excelben történő elvégzéséhez először is szüksége van a megfelelő adatokra. Példánkban olyan helyzetet feltételezünk, amelyben a hatóanyagok sikerességi arányát elemzi. Ismert, hogy az átlagos sikerességi arány korábban 59% volt, 19 %-os szórással. Először is be kell vinnie az adatokat egy Excel táblázatba.
Győződjön meg róla, hogy az adatait oszlopokba rendezte, hogy később könnyen hozzáférhessen. A világos áttekintés segít abban, hogy könnyebben megértse az egyes lépéseket.
A teszt áttekintése
Az 1-SP teszt annak ellenőrzésére szolgál, hogy az átlagos sikerességi érték jelentősen eltér-e egy megadott értéktől. Ebben az esetben azt vizsgáljuk, hogy az 59%-os sikerességi arány a jövőben jelentősen növelhető-e.
Hipotézisek megfogalmazása
A teszthez megfogalmazott hipotézisek döntő fontosságúak:
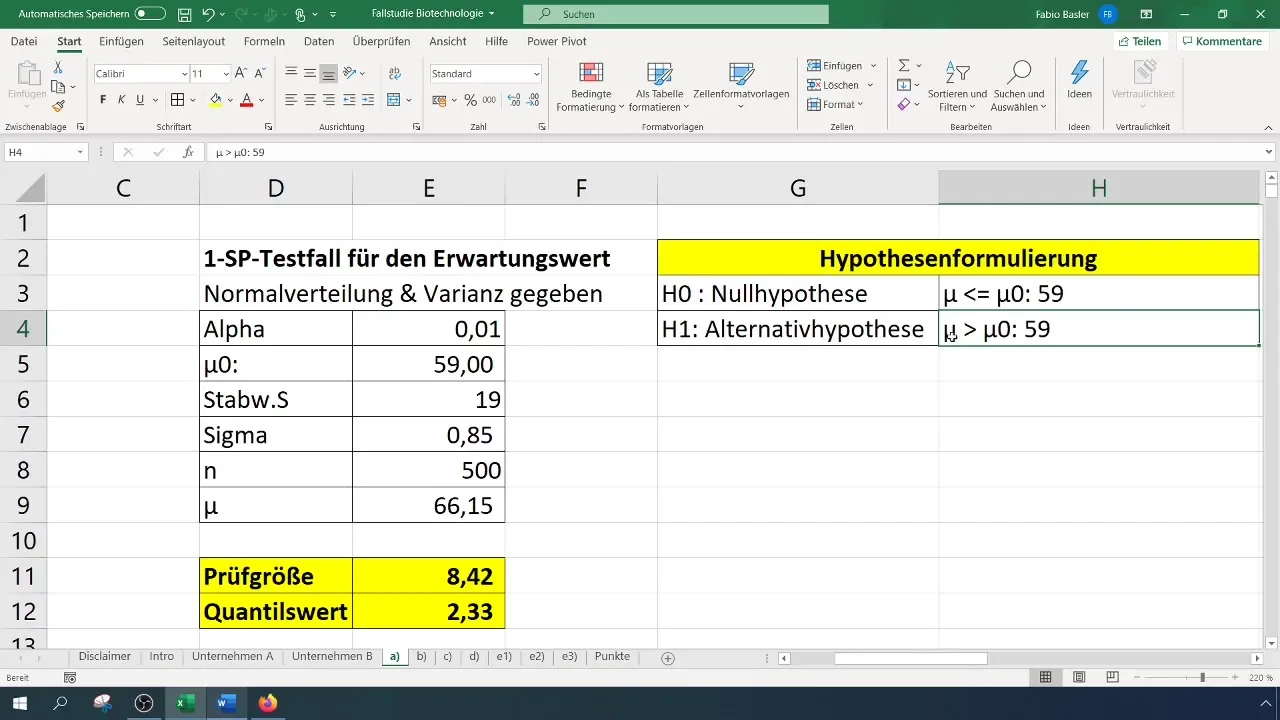
- Nullhipotézis (H0): A valódi várható érték 59-cel egyenlő (σ = 59%).
- Alternatív hipotézis (H1): A valódi várható érték nagyobb, mint 59%.
A hipotézisek megfogalmazásakor arra kell összpontosítani, hogy pontosan mit kell tesztelni, és ez hogyan jelenik meg az Ön kontextusában.
Fontos, hogy egyértelműen felismerjük a nullhipotézis és az alternatív hipotézis közötti különbséget, mivel ezek képezik a következő számítások alapját.
A minta összegyűjtése
A tesztünkhöz 500 hatóanyagból álló mintát veszünk. Fontos megjegyezni, hogy a minta kiválasztása reprezentatív legyen, és a megfelelő módszerrel garantálnia kell, hogy eredményei reálisan átvihetők legyenek a teljes populációra.
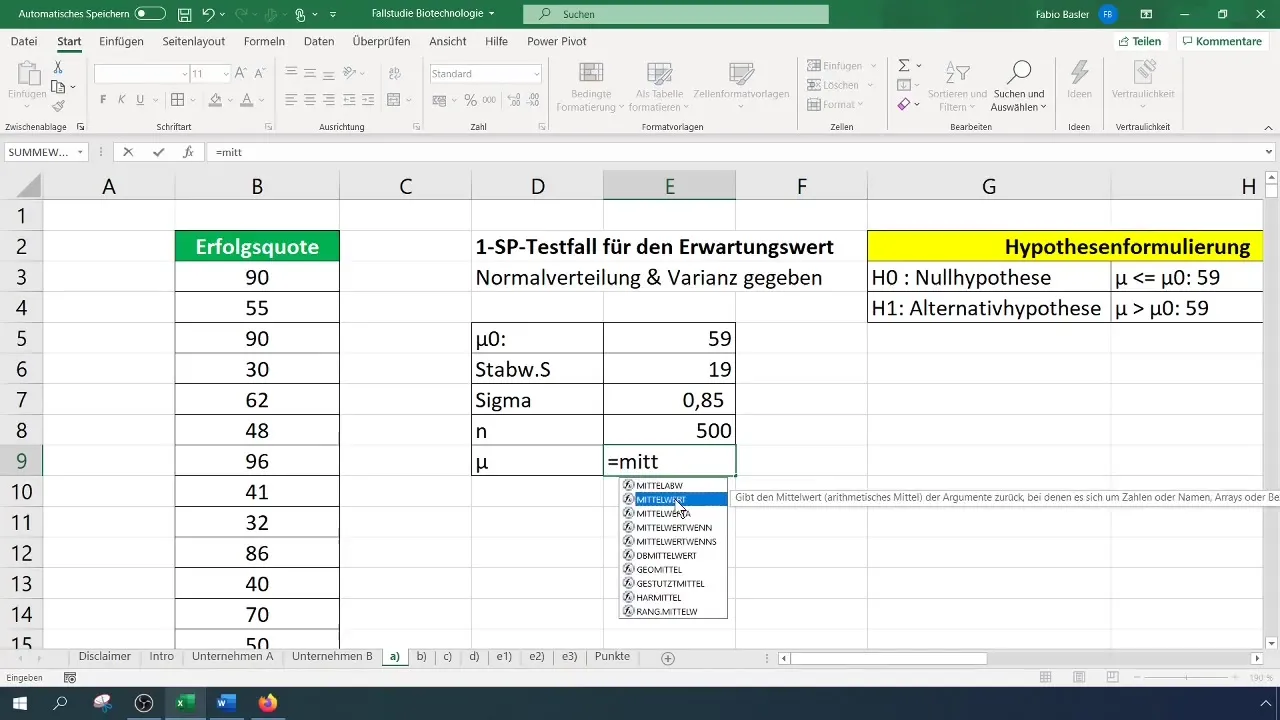
A vizsgálathoz először számítsa ki a számtani átlagot. Ez könnyen elvégezhető az Excel megfelelő képletének használatával.
A vizsgálati változó kiszámítása
Az 1-SP teszt vizsgálati változóját a következő képlettel kell meghatározni
[ Z = \frac{\bar{x} - \mu_0}{\sigma/\sqrt{n}}] ]
Itt (\bar{x}) a minta átlagértékét, (\mu_0) a feltételezett átlagértéket (ebben az esetben 59), (\sigma) a szórást (itt 19) és (n) a minták számát (500) jelöli.
Miután beillesztette az értékeket a képletbe, számítsa ki a tesztstatisztikát, hogy megállapítsa, szignifikáns-e vagy sem.
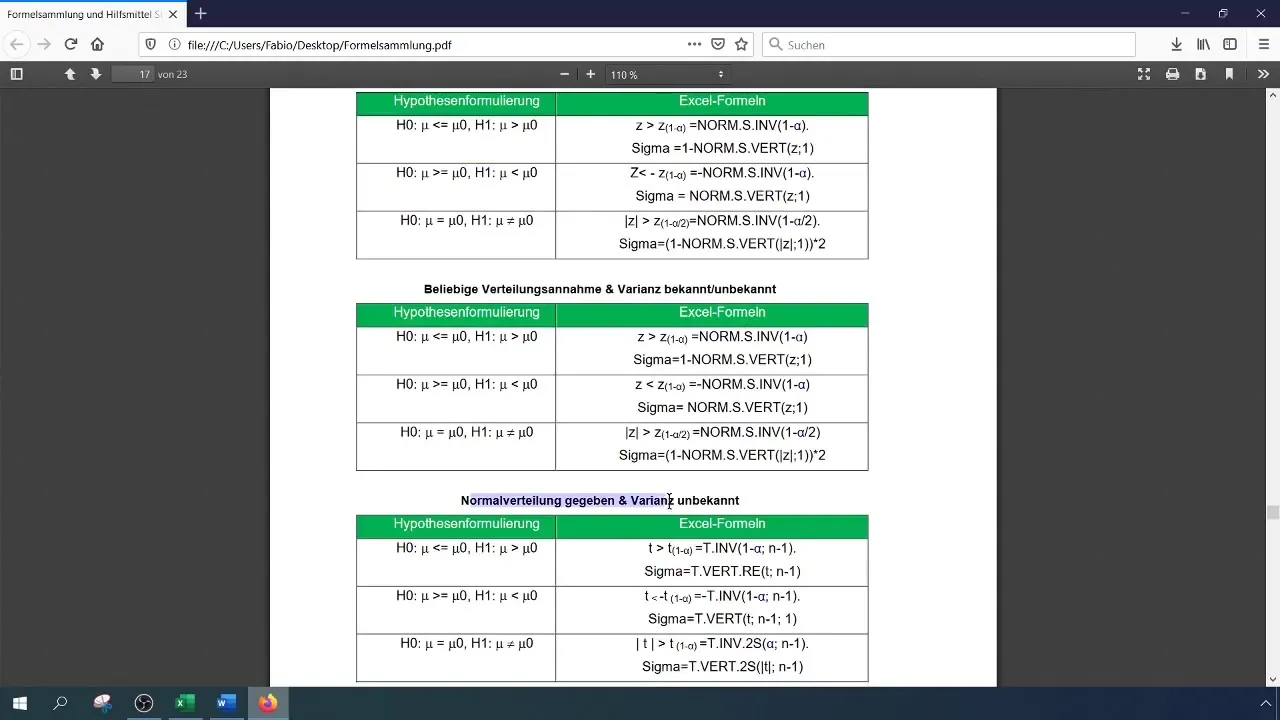
A kritikus érték meghatározása
Az 1%-os (0,01) szignifikancia szint esetén le kell olvasnia vagy ki kell számolnia a kritikus értéket. Ezt az Excelben a NORM.S.INV függvénnyel teheti meg.
A képlet a következő:
[ \text{NORM.S.INV}(1 - \alpha)] ]
Ahol (\alpha) a szignifikancia szint (0,01). A meghatározott értéket a vizsgálati változóval való összehasonlítás alapjául használjuk.
A teszt elvégzése
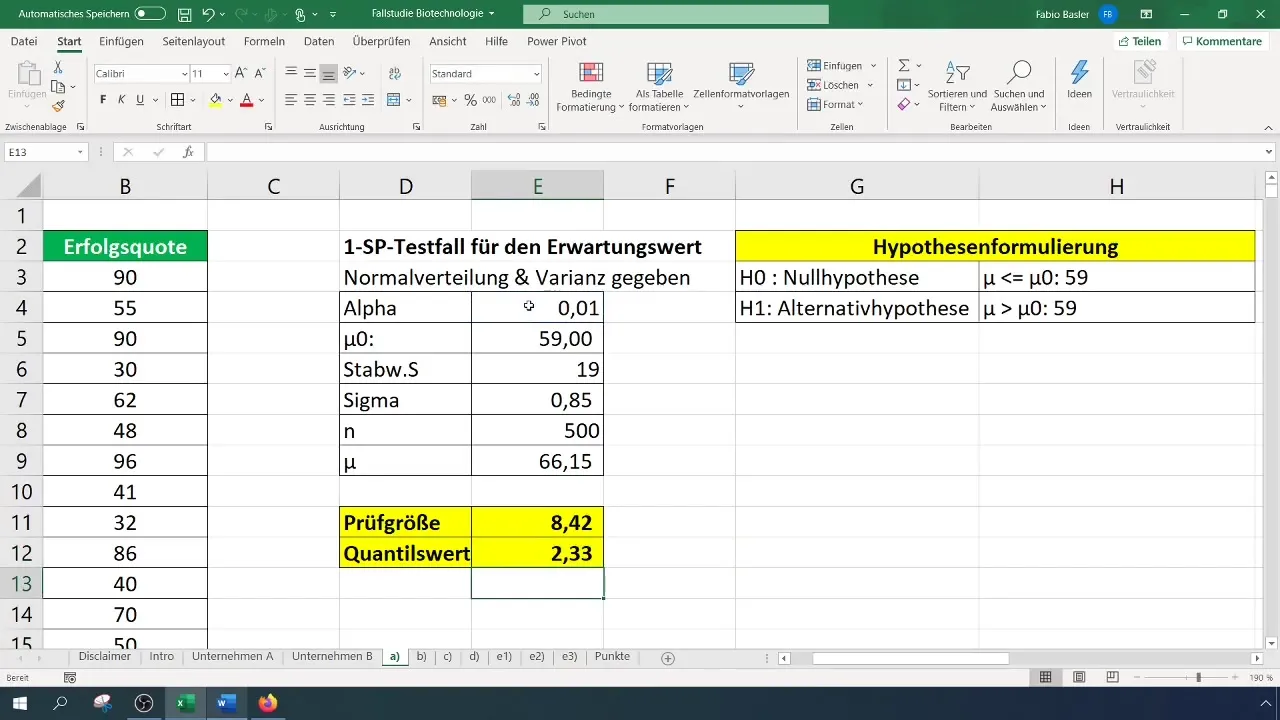
Most, hogy már rendelkezik a tesztstatisztikával és a kritikus értékkel is, hasonlítsa össze a kettőt:
- Ha a tesztstatisztika nagyobb, mint a kritikus érték, a nullhipotézist elvetjük.
- Ellenkező esetben a nullhipotézist nem lehet elutasítani.
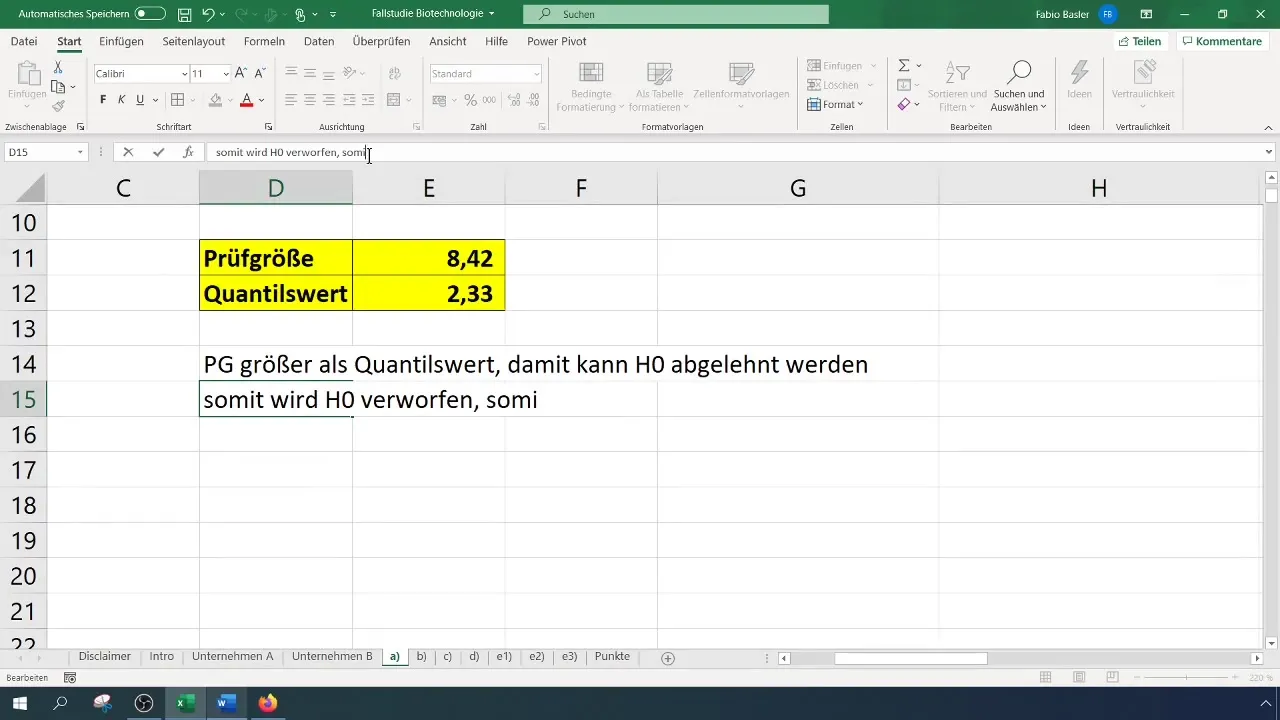
Esetünkben ez azt eredményezi, hogy a tesztstatisztika 8,4, ami meghaladja a 2,33-as kritikus értéket. A nullhipotézist tehát elvethetjük. Ez azt jelzi, hogy a sikerességi arány jelentősen javult.
Az eredmények értelmezése
Miután elvégezte a tesztet és megkapta az eredményeket, azokat világos kontextusban kell értelmeznie. A nullhipotézis elutasítása azt jelenti, hogy a vizsgált új érték szignifikánsan eltér a korábbi értéktől, ebben az esetben az 59%-tól.
Ez az információ rendkívül fontos a szervezet stratégiai döntéshozatalához. Megerősíti, hogy a sikerességi arány javítására tett erőfeszítések eredményesek voltak.
Összefoglaló
Ebben a bemutatóban megtanulta, hogyan végezhet 1-SP tesztet a várható értékre az Excelben. Egy esettanulmány segítségével végigkövethette a lépéseket a hipotézisek felállításától az adatok kiszámításáig és az eredmények értelmezéséig. Ez a tudás nemcsak a tudományos elemzésekhez, hanem a vállalati gyakorlati alkalmazásokhoz is értékes.
Gyakran ismételt kérdések
Mi az az 1-SPteszt? Az 1-SP teszt egy olyan statisztikai teszt, amellyel azt lehet ellenőrizni, hogy egy minta átlagértéke szignifikánsan eltér-e egy megadott értéktől.
Hogyan fogalmazok meg hipotéziseket a teszthez? A hipotézisek egy nullhipotézisből (H0) és egy alternatív hipotézisből (H1) állnak, amelyek dokumentálják a vizsgálandó feltételt.
Hogyan számolom ki a tesztstatisztikát? A tesztstatisztikát a képlet ( Z = \frac{\bar{x} - \mu_0}{\sigma/\sqrt{n}} ) alapján határozzuk meg.
Mi történik, ha a tesztstatisztika nagyobb, mint a kritikus érték? Haa tesztstatisztika nagyobb, mint a kritikus érték, a nullhipotézist elvetjük.
Milyen szerepe van a szignifikancia-szintnek?A szignifikancia-szint azt a valószínűséget jelzi, amellyel hajlandóak vagyunk elfogadni egy hibát, ha tévesen utasítjuk el a nullhipotézist.


