A kétmintás t-próba egy lényeges eszköz a statisztikában, amikor két középérték közötti különbséget szeretnél vizsgálni. Ebben a tutorialban megtudhatod, hogyan végezheted el ezt a tesztet egyszerűen és hatékonyan az Excel segítségével. Egy biotechnológiai példa segítségével megtanulod, hogyan hasonlíthatod össze és elemzheted statisztikailag két versenyző vállalat sikerarányát.
Legfontosabb felismerések
- A kétmintás t-próba alkalmazása a két középérték különbségének elemzéséhez.
- Hipotézisek megfogalmazása és ellenőrzése.
- Az Excel használata az eredmények számítására és megjelenítésére.
Lépésről lépésre
Először is kezdjük a szükséges adatok előállításával és a teszt végrehajtásával az Excelben.
Lépés 1: Adatok előkészítése
Kezdd el a vállalatok sikerarányára vonatkozó nyers adatok gyűjtését. Feltételezve, hogy rendelkezel az A és B vállalat adataival. Mindegyik vállalathoz 100 mintát veszel.

Lépés 2: Mintaszám és középértékek kiszámítása
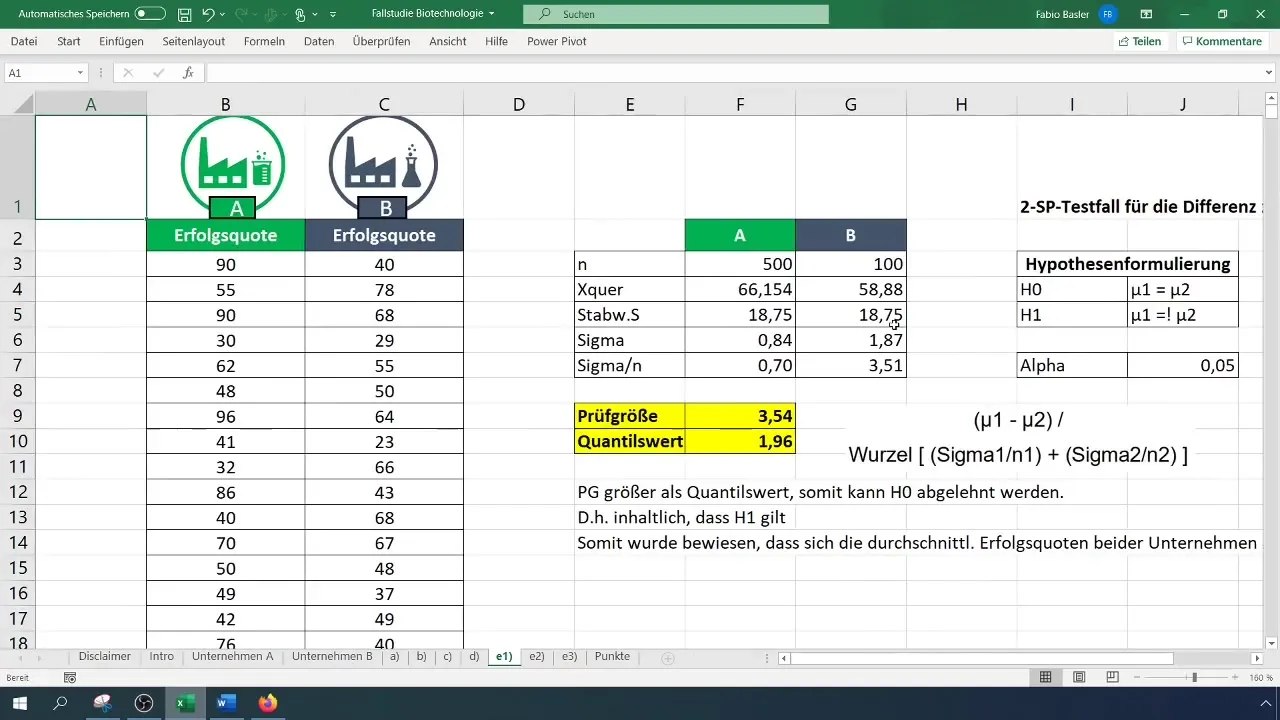
Készíts egy táblázatot az Excelben, ahol összehasonlíthatod a mintákat és a középértékeket. Először számold ki a mintaszámot (N) mindkét vállalathoz, valamint a középértéket (X).

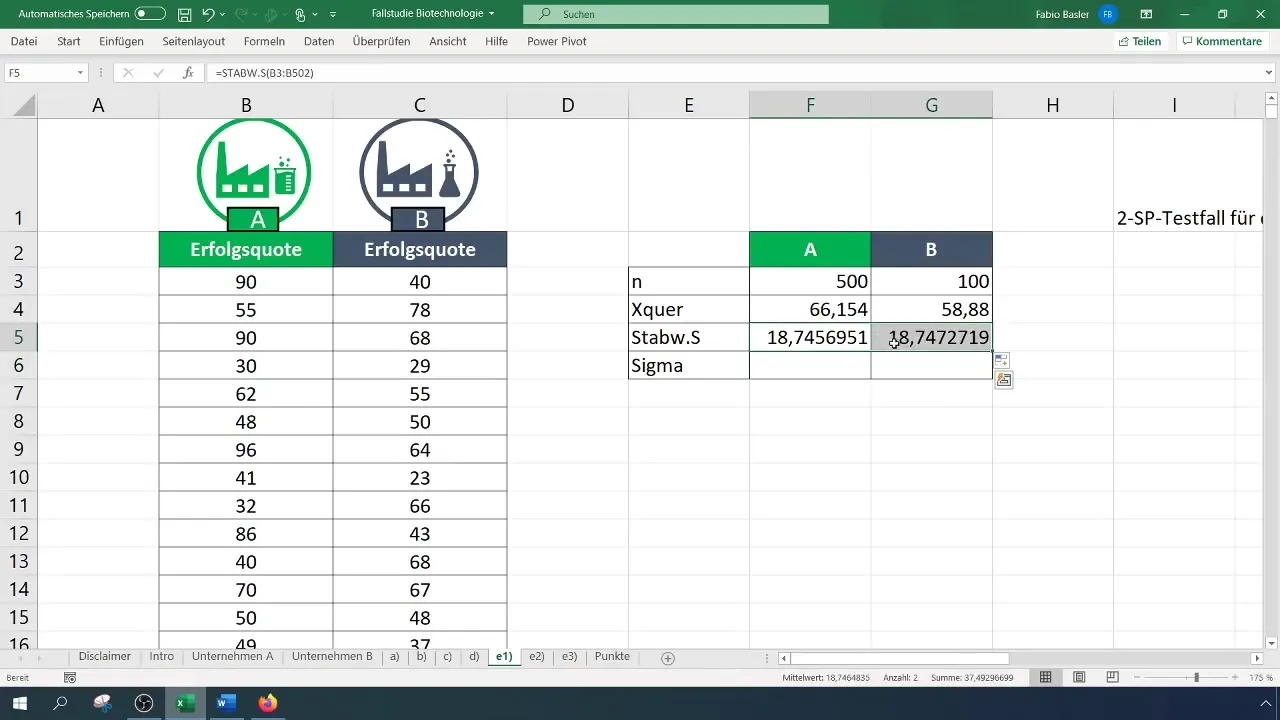
Lépés 3: Szórások meghatározása
Számold ki a szórásokat mindkét vállalathoz. Ezek az értékek fontosak a variancia és a további számítások szempontjából.
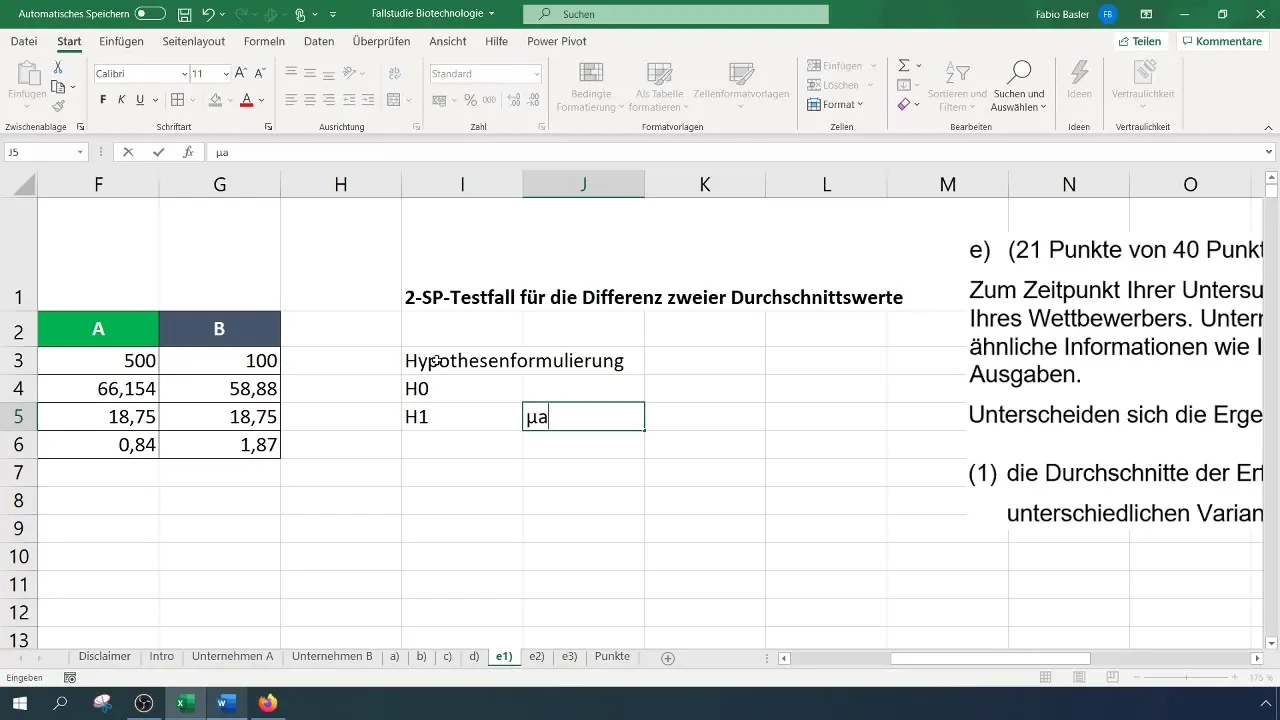
Lépés 4: Hipotézisek megfogalmazása
Fogalmazd meg a nulla hipotézist (H_0): Az A és B vállalatok sikerarányának átlagértékei megegyeznek. Az alternatív hipotézis (H_1): A sikerarányok átlagértékei különböznek.
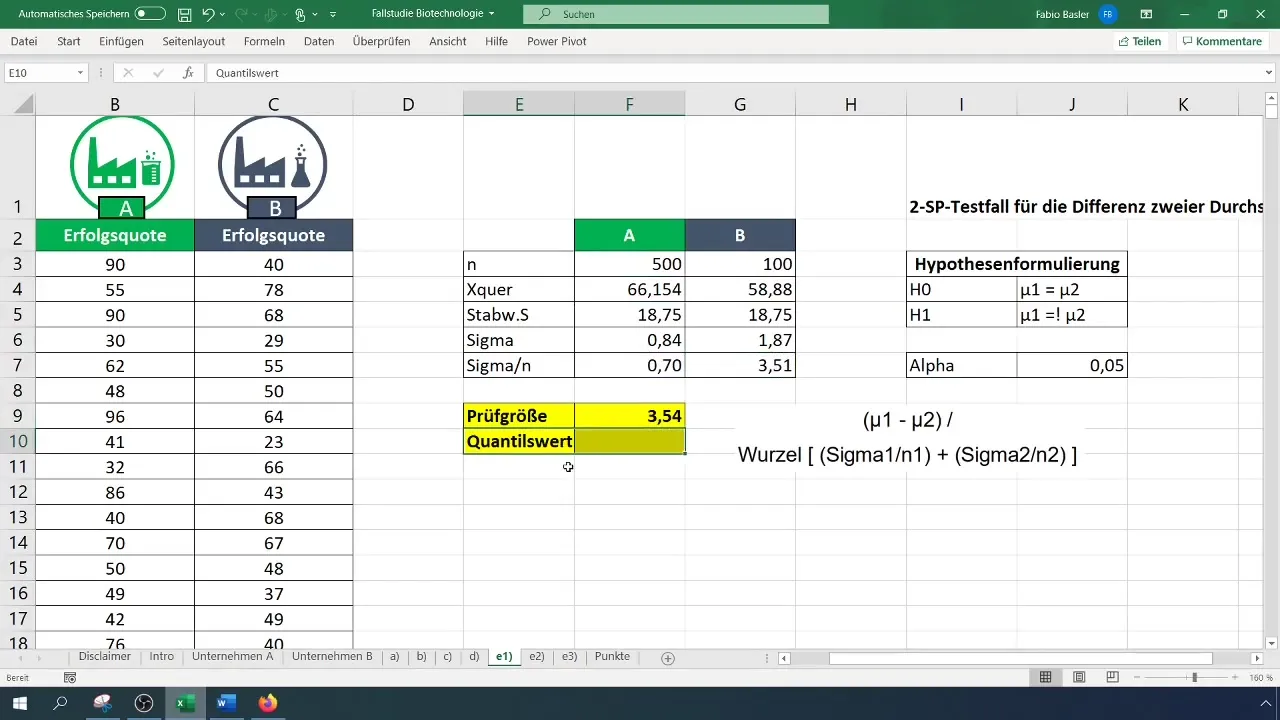
Lépés 5: Próbaméret kiszámítása
A próbaméret kiszámításához használd a t-próba képletét. Számold ki a középértékek különbségét és oszd el a gyökérrel a mintaszámok varianciájának összegét.
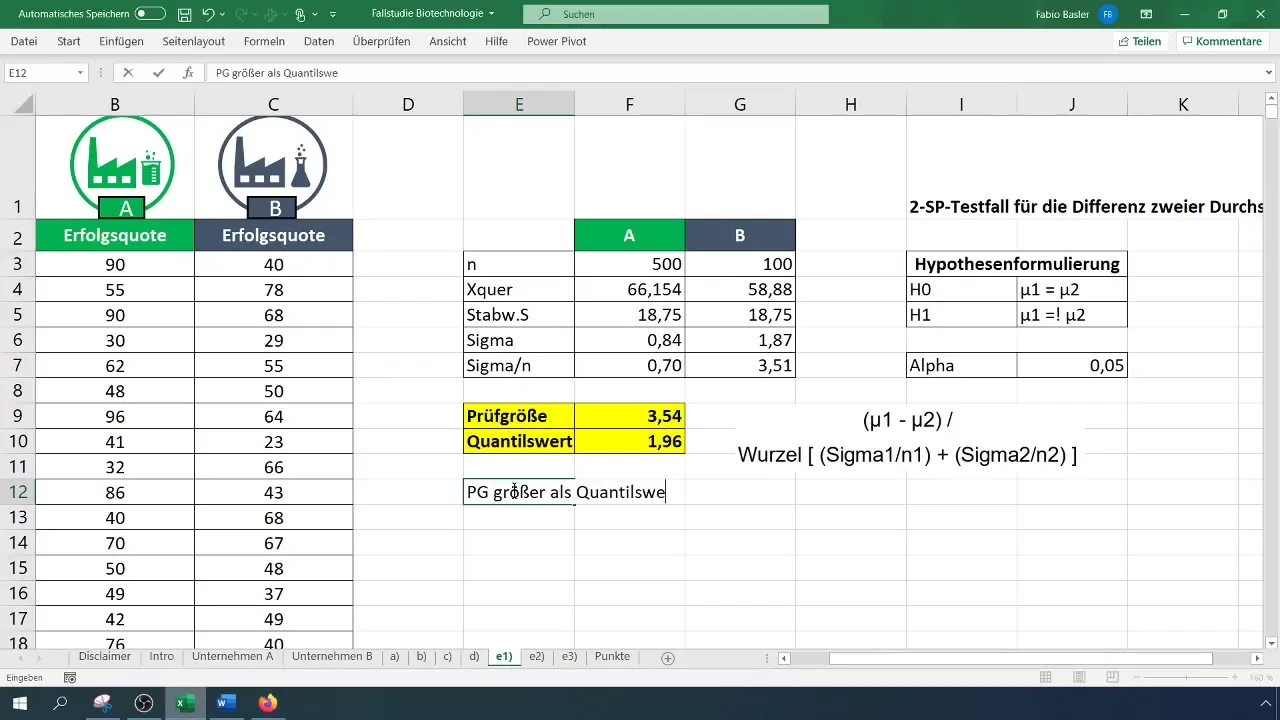
Lépés 6: Kritikus érték meghatározása
Használd a kétoldalú t-eloszlást a kritikus érték meghatározásához. Állítsd az Alfa szintet 0,05-re. Nézd meg az t-eloszlás táblázatot, vagy számold ki a faktort közvetlenül az Excelben.
Lépés 7: Döntés a hipotézisről
Hasonlítsd össze a kiszámított próbaméretet a kritikus értékkel. Ha a próbaméret nagyobb, mint a kritikus érték, elutasítsd a null hipotézist (H_0) és ezzel megerősítsd az alternatív hipotézist (H_1).
Lépés 8: Eredmények értelmezése
Végül értelmezd az eredményt. Ebben a példában a két vállalat átlagos sikerarányát szignifikánsan különbözőnek találták.
Összefoglalás
Megtanultad, hogyan végezhetsz el egy kétmintás t-próbát az Excelben annak érdekében, hogy megvizsgáld két csoport középértékeinek különbségeit. A lépések adataink előkészítésétől a hipotézisek megfogalmazásán át az eredmények értelmezéséig döntő fontosságúak ahhoz, hogy érvényes és tájékozott döntéseket hozz.
Gyakran Ismételt Kérdések
Mi az a kétmintás t-próba?Egy kétmintás t-próba összehasonlítja két csoport középértékeit annak érdekében, hogy megállapítsa, jelentős különbség van-e közöttük.
Hogyan fogalmazok hipotéziseket?A nulla hipotézis (H_0) szerint a középértékek azonosak, míg az alternatív hipotézis (H_1) szerint eltérnek.
Hogyan számítom ki a próbaméretet?A próbaméretet a középértékek különbsége osztva a minták varianciájának gyökével számoljuk ki.
Mit csinálok a számítások után?Hasonlítsd össze a próbaméretet a kritikus értékkel, hogy eldöntsd elutasíthatod-e a null hipotézist.
Miért fontos a szórás?A szórás segít megérteni az adatok változékonyságát, amely lényeges a próbaméret kiszámításához.


