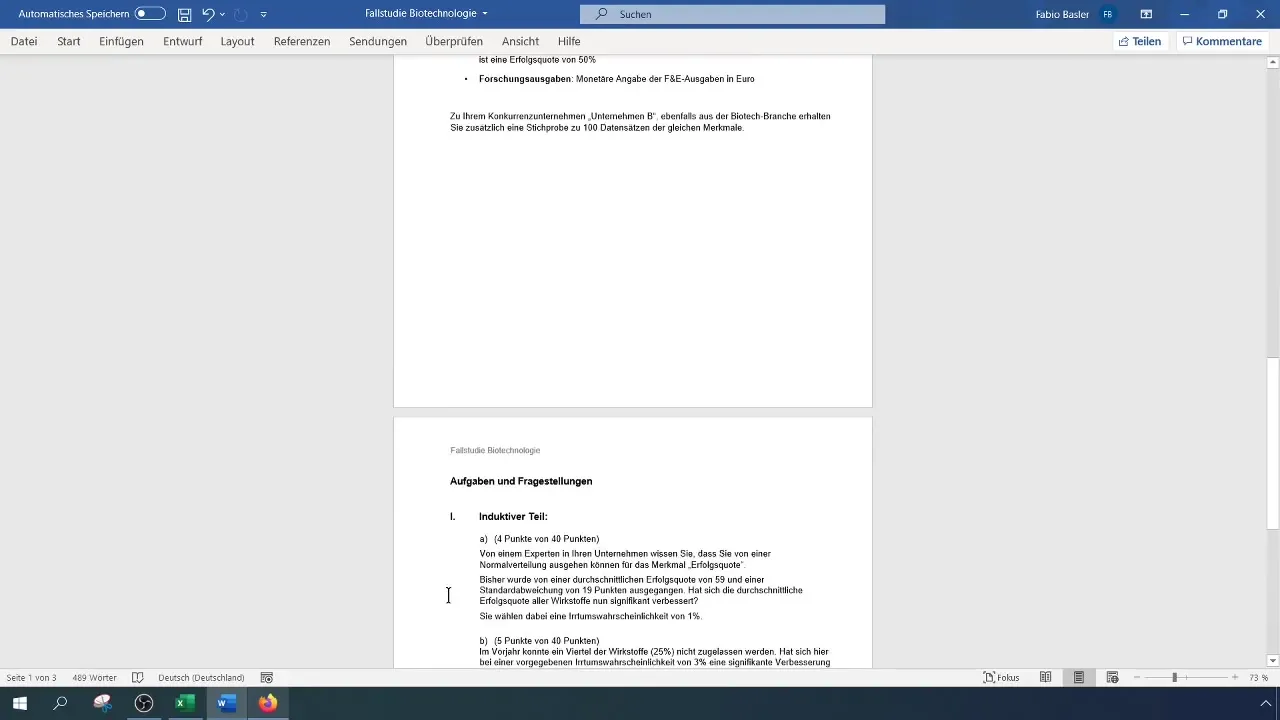
A statisztikai elemzések keretében a hipotézisteszt egy központi eszköz, amely lehetőséget nyújt különböző feltételek ellenőrzésére egy adathalmazon. Ebben az útmutatóban megtanulod, hogyan végezhetsz egymintás tesztet a varianciára az Excel segítségével. Az elméleti alapokon és a gyakorlati lépéseken keresztül azt fogod megtanulni, hogy hogyan tesztelheted a mintád varianciáját szignifikáns változások szempontjából.
Részletek
- A teszt azt vizsgálja, hogy egy ismert szórás szignifikánsan eltér-e egy új szórástól.
- A variancia hipotézistesztje egymintás megközelítést alkalmaz.
- A számítás magában foglalja a hipotézisek meghatározását, a tesztméret meghatározását és az összehasonlítást a Chi-négyzet-eloszlásból származó kritikus értékkel.
Lépésről lépésre útmutató
Lépés 1: Adathalmaz előkészítése
Először importáld vagy manuálisan írd be az adathalmazodat az Excelbe. Az adathalmaznak tartalmaznia kell azokat az értékeket, amelyek relevánsak a variancia számításához. Ehhez nyisd meg az Excelt, és hozz létre egy új táblázatot. Írd be az értékeket egy oszlopba.

Lépés 2: Standardabweichung és variancia számítása
A variancia kiszámításához használd a mintád standardabweichungját. Ha ismert standardabweichungod van (ebben az esetben 22), négyzetre emelve ezt az értéket megkapod a történelmi varianciát (σ0²). Használd a következő képletet:
Variancia (σ0²) = (Standardabweichung)²
Ezt egyszerűen beírhatod egy cellába az Excelben.
Lépés 3: Hipotézisek megfogalmazása
Most megfogalmazod a nullhipotézist (H0) és az alternatív hipotézist (H1). A nullhipotézis szerint a variancia megegyezik az ismert varianciával, az alternatív hipotézis pedig azt állítja, hogy a variancia szignifikánsan csökkent. Ezt írod le:
- H0: σ² = 484
- H1: σ² < 484
Lépés 4: Prüfgröße számítása
A Prüfgröße (χ²) kiszámítása a következő képlet szerint történik:
χ² = (n - 1) * (σ1² / σ0²)
Itt n a mintaadatpontok száma, σ1 pedig az általad becslés alapján származó standardabweichás a mintádból. Az Excelben ezt az egy megfelelő cella hivatkozásával kiszámíthatod.

Lépés 5: Kritikus érték meghatározása
A teszt kritikus értékének meghatározásához szükséged lesz a Chi-négyzet-eloszlásra. Ezt az értéket az Excelben a CHISQ.INV() funkcióval tudod kiszámítani, ahol a kívánt szignifikancia szintet (itt 2,5% egyoldalú teszthez) és a szabadsági fokot (n-1) használod.
Lépés 6: Prüfgröße összehasonlítása a kritikus értékkel
Összehasonlítod a kiszámított Prüfgröße-t (χ²) a kritikus értékkel. Ha a Prüfgröße kisebb, mint a kritikus érték, akkor elutasíthatod az H0 hipotézist. Ez azt jelenti, hogy szignifikáns különbség van, és a variancia csökkent.
Lépés 7: Következtetés levonása
A teszted alapján most megfogalmazhatsz egy következtetést. Ha elutasítják az H0-t, tisztázni kell, hogy a populációdban a variancia szignifikánsan kisebb, mint az eredeti variancia. Dokumentáld az eredményeidet, és számold fel őket egy beszámolóban.
Összefoglalás
Ebben az útmutatóban megtanultad, hogyan végezhetsz hatékonyan egymintás tesztet a varianciára az Excelben. A gyakorlati alkalmazás segítségével az elméleti alapokon keresztül betekintést kaphatsz az adataidba.
Gyakran Ismételt Kérdések
Hogyan számítható ki a variancia az Excelben?A variancia kiszámítható az Excelben a VAR.P() képlet használatával a teljes populáció vagy a VAR.S() az egy adott minta esetére.
Mi a különbség az H0 és az H1 között?A H0 a nullhipotézis, amely szerint nincs különbség. Az H1 az alternatív hipotézis, amely jelentős különbséget feltételez.
Mit kell tennem, ha nem vetik el az H0-t?Ha az H0-t nem vetik el, az azt jelenti, hogy az adatok nem szolgáltatnak elég bizonyítékot arra, hogy állítani lehessen, a variancia szignifikánsan eltér az ismert varianciától.


