Fontos, hogy üzleti és értékesítési környezetben adatelemzéseken alapuló megalapozott döntéseket hozz. Egy kétoldalú bizalmi intervallum lehetőséget nyújt arra, hogy meghatározd azt a tartományt, ahol egy paraméter valódi átlagértékét bizonyos valószínűséggel megtalálod. Ebben az útmutatóban megmutatom, hogyan számíthatod ki az Intervallumhatárokat a területi értékesítési csapat heti árbevételére 93%-os bizalom valószínűség mellett Excel-lel.
Legrkellőbb felismerések
A kétoldalú bizalmi intervallum lényeges aspektusai közé tartoznak:
- A középérték kiszámítása a paraméter becsült értékének.
- Amint meghatározzák a standard hibát a mintában.
- A képletek alkalmazása az intervallum alsó- és felső határának meghatározására.
- A bizalom valószínűség figyelembevétele az intervallum elhelyezéséhez.
Lépésről lépésre
Először is szükséged lesz egy szilárd megértésre a fogalmakra és a lépésekre, amelyek leírják ezt a folyamatot.
1. lépés: Adatok előkészítése
Először elkészíted az A értékesítési csapat adatait. Szűrd ki a releváns adatokat, és másold be azokat a Excel-dokumentumba.
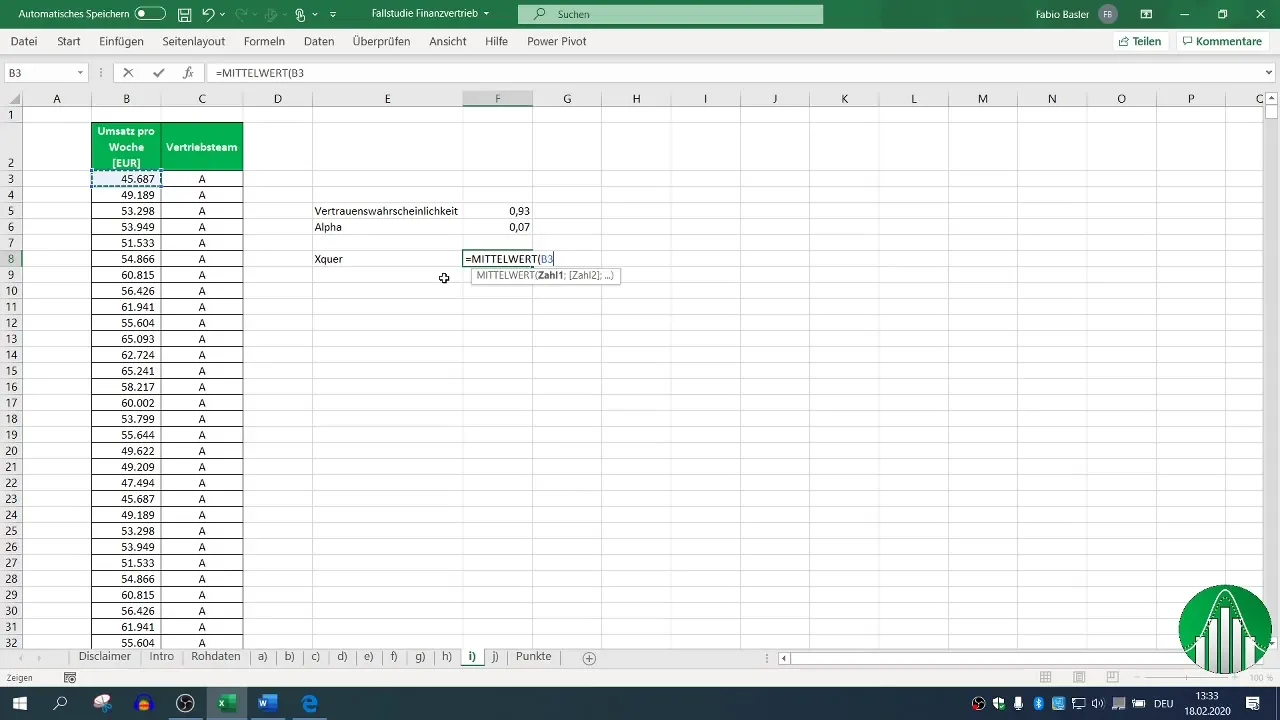
2. lépés: Középérték számítása
A bizalmi intervallum kiszámításához az első lépés a középérték meghatározása, amely becslésként szolgál az elvárt árbevételre. Excelben ezt a =ÁTLAG(Tartomány) képlettel teheted meg, ahol "Tartomány" az a(zok) cella(k), amely(t) tartalmazzák az A értékesítési csapat heti árbevételi adatait.
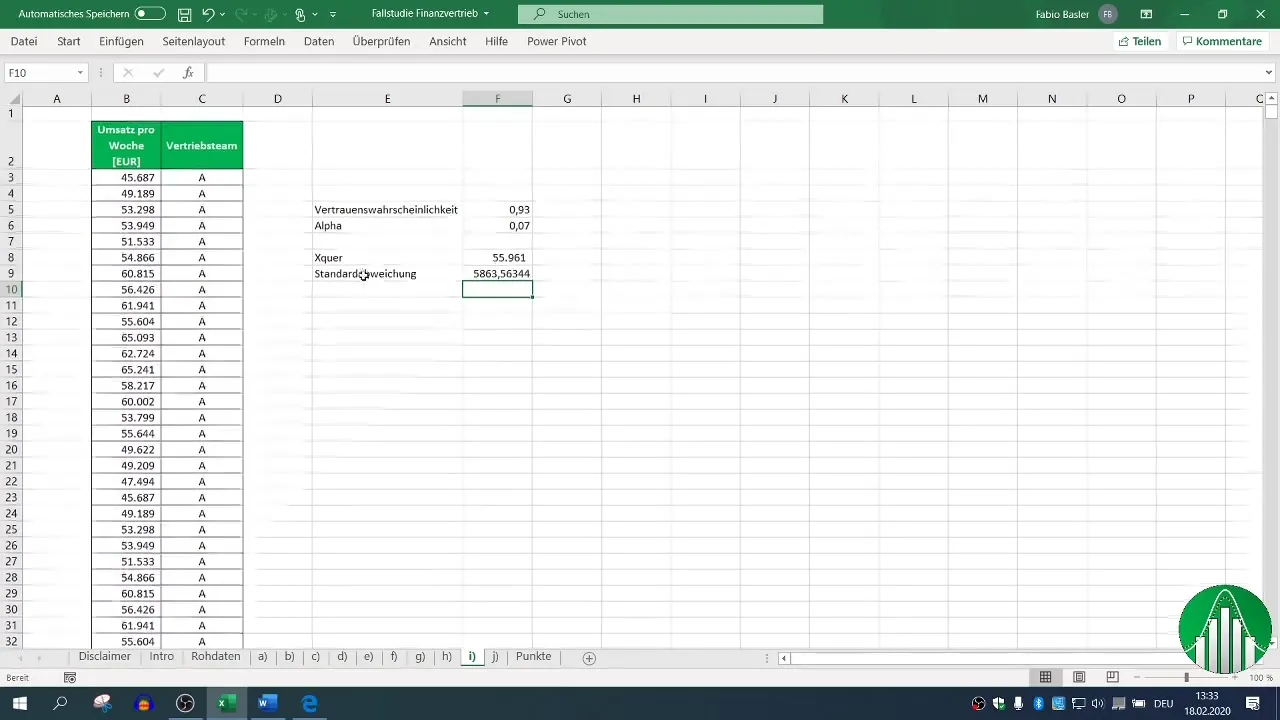
3. lépés: Standard hiba számítása
A szórás (σ) számítása fontos a kétoldalú bizalmi intervallum számításakor. Excelben a szórás =SZÓRÁS.S(Tartomány) képlet segítségével számítható ki. Győződj meg róla, hogy megfelelő képletet választasz a mintaszórásra.
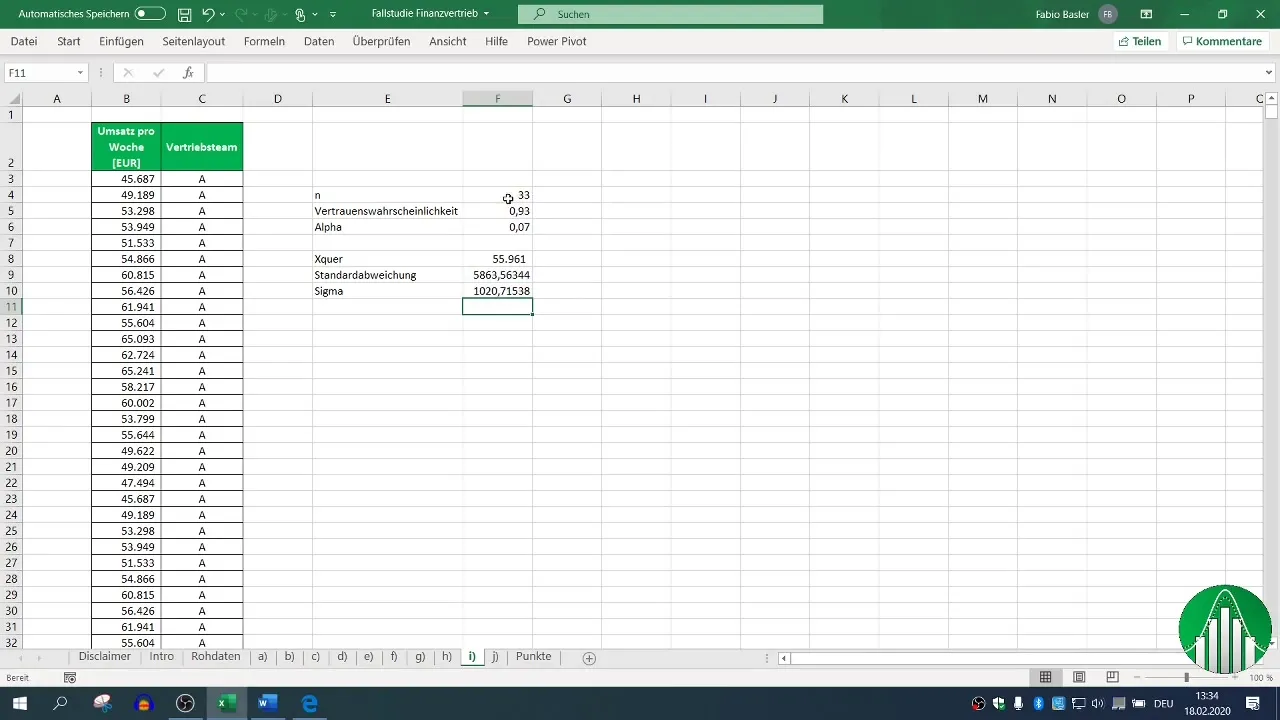
4. lépés: Mintanagyság meghatározása
Ezután meg kell határoznod a mintanagyságot (n). Add össze az A értékesítési csapat számára gyűjtött adatok számát. Ebben az példában 33 adatot tekintünk.
5. lépés: Középérték szórásának (σ_m) számítása
Az intervallum számításához fontos a középérték szórásának számítása, amely egyszerűen a szórás osztva a mintanagyság négyzetgyökével.
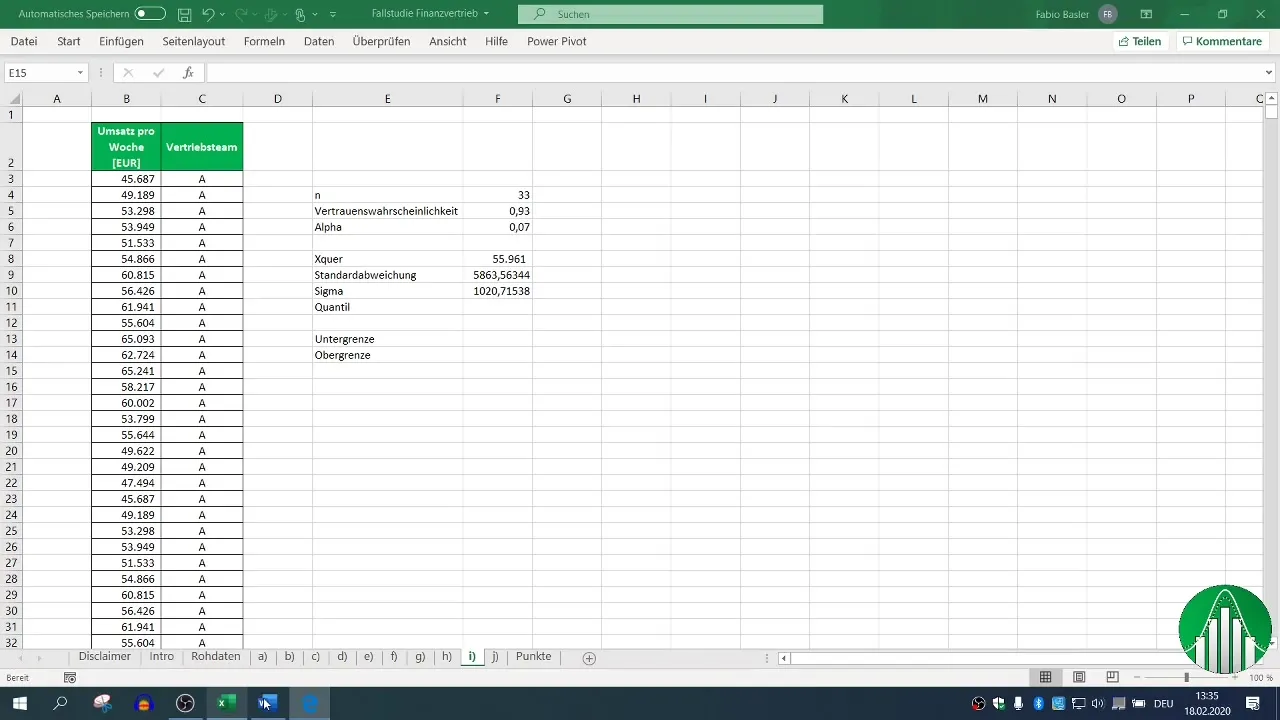
6. lépés: Kvantil meghatározása
A kétoldalú bizalmi intervallum számításához szükséged lesz a kvantilra. Mivel 93%-os bizalomvalószínűséget adsz meg, az α 7% és a kvantil eloszlását az Excel függvény segítségével találod meg.
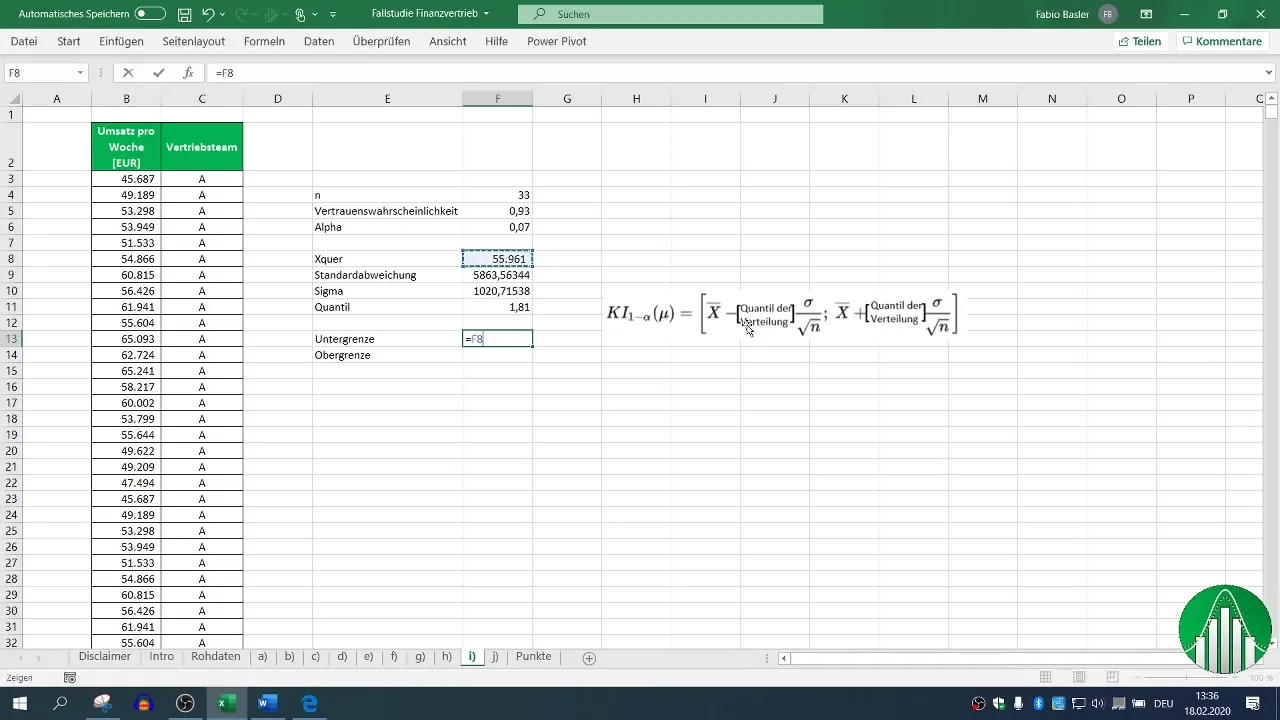
7. lépés: Alsó határ számítása
Most kiszámítjuk a bizalmi intervallum alsó határát. Ehhez vedd ki a középértékből (x̄) a kvantil és a középérték szórásának szorzatát.
8. lépés: Felső határ számítása
A felső határ hasonlóan számítható, de a szorzatot hozzáadsz, nem pedig kivonod.
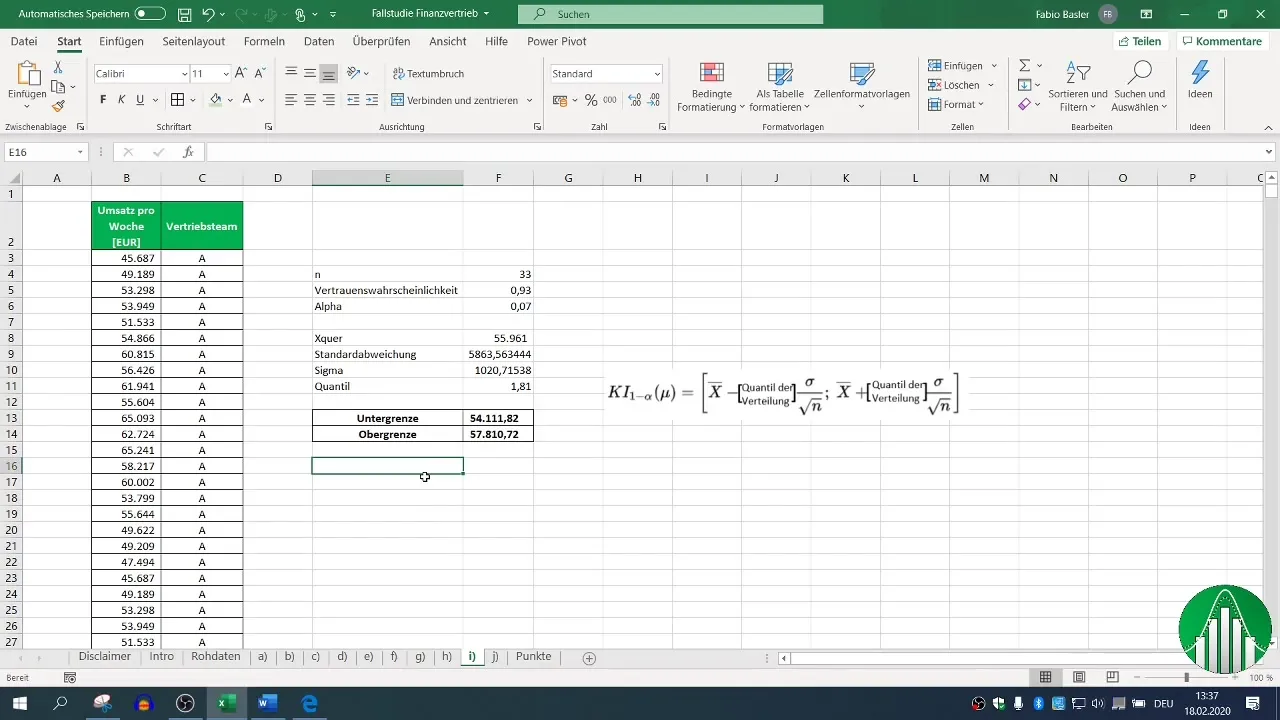
9. lépés: Eredmény értelmezése
Ezen számítások után megkapod az A értékesítési csapat heti árbevételének kétoldalú bizalmi intervallumát. Az példánk esetében az intervallum 54,111 és 57,810 között van. Ez azt jelenti, hogy 93%-os bizalomvalószínűséggel a valódi átlagos árbevétel ezen a tartományon belül található.
Összefoglalás
A kétoldalú bizalmi intervallum pontos számításával pontos állításokat tehetsz a jövőbeli árbevételről. Megtanultad, hogyan kell előkészíteni az adatokat, meghatározni a középértéket, a szórást, és végül az intervallum határait meghatározni. Ezzel a módszerrel adatalapú döntéseket hozhatsz az értékesítési területeden.
Gyakran Ismételt Kérdések
Mi az a kétoldalú megbízhatósági intervallum?Ez egy intervallum, amely egy paraméter becslését egy adott valószínűséggel tartalmazza.
Mit tegyek, ha nincs normál eloszlás?Ha nincs normál eloszlás, akkor használhatsz bármilyen eloszlásfeltevést.
Miért fontos a kvantilis?A kvantilis segít meghatározni a megbízhatósági intervallum felső és alsó határát.


