A statisztikai hipotézispróbák elengedhetetlen eszközök a vállalatok számára, hogy megalapozott döntéseket hozzanak. A következő szakaszban bemutatjuk neked, hogyan végezheted el a Kétmintás-F-próbát Excelben, hogy ellenőrizd a hipotéziseid érvényességét az értékesítési adatok varianciájára vonatkozóan. Ez az útmutató lépésről lépésre vezet végig a folyamaton, hogy magabiztosan alkalmazhasd az elsajátított technikákat.
Legfontosabb felismerések
- A Kétmintás-F-próba azt használjuk, hogy összehasonlítsuk két adatcsoport szórásait.
- A cél az, hogy megvizsgáljuk, hogy az aktuális értékesítési adatok szórása eltér-e egy feltételezett értéktől.
- Az Excel lehetőséget biztosít arra, hogy elvégezzük a szükséges számításokat és összehasonlításokat.
Lépésről lépésre útmutató
1. Adatok előkészítése
Mielőtt elkezdenéd a próbát, győződj meg róla, hogy az adataid elő vannak készítve. Fontos, hogy eltávolítsd a szűrőket, hogy figyelembe tudd venni az összes releváns adatot. Kezdd azzal, hogy kiválasztod az adatokat a megfelelő oszlopokban.

2. Paraméterek meghatározása
Határozd meg a próbád paramétereit. Tudnod kell, hogy hány adatpontot elemzünk. Az adatok száz értékesítési számot testesítenek meg, amelyek normális eloszlásúak.

3. Korábbi varianciaérték rögzítése
A múltból ismert variancia- vagy értékesítési érték kulcsfontosságú tényező az elemzésedben. Ebben az példában, a korábbi érték 116 millió euró volt hetente.
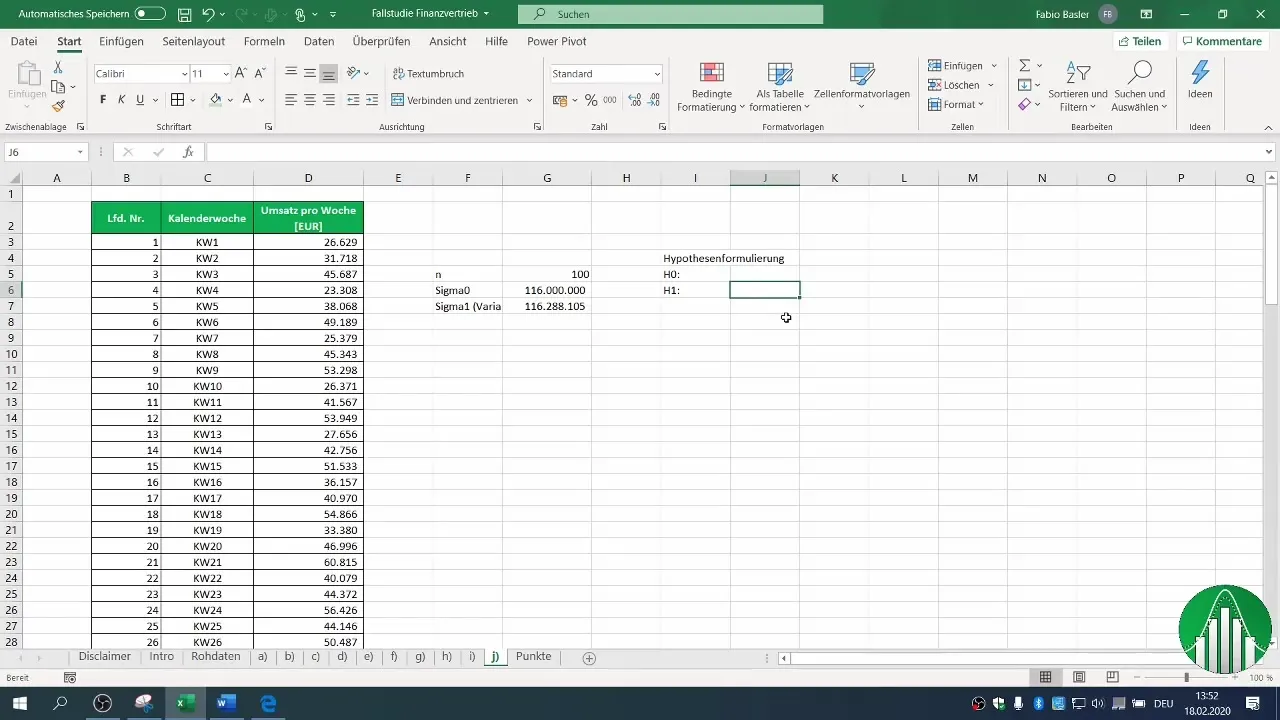
4. Hipotézisek megfogalmazása
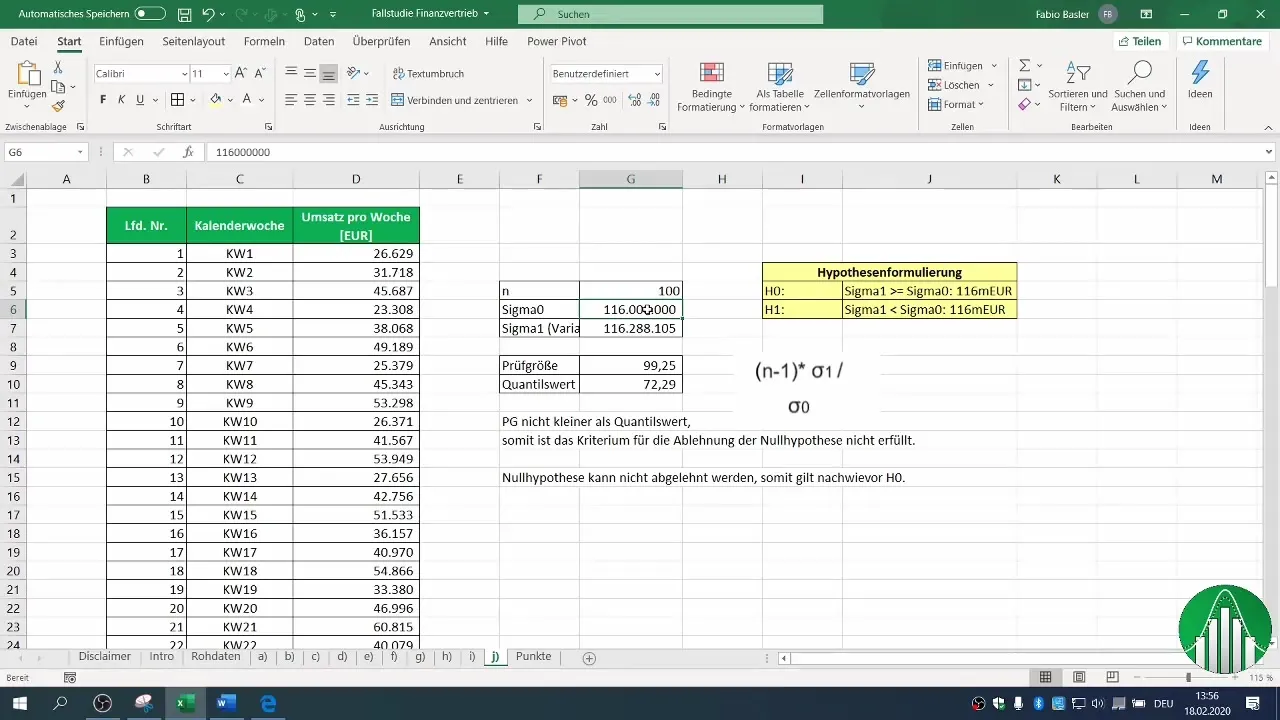
Fogalmazd meg a nulla hipotézist (H0) és az alternatív hipotézist (H1). Ebben az esetben a H0 állítja, hogy a variancia egyenlő vagy nagyobb, mint 116 millió, míg az H1 azt feltételezi, hogy a variancia csökkent.
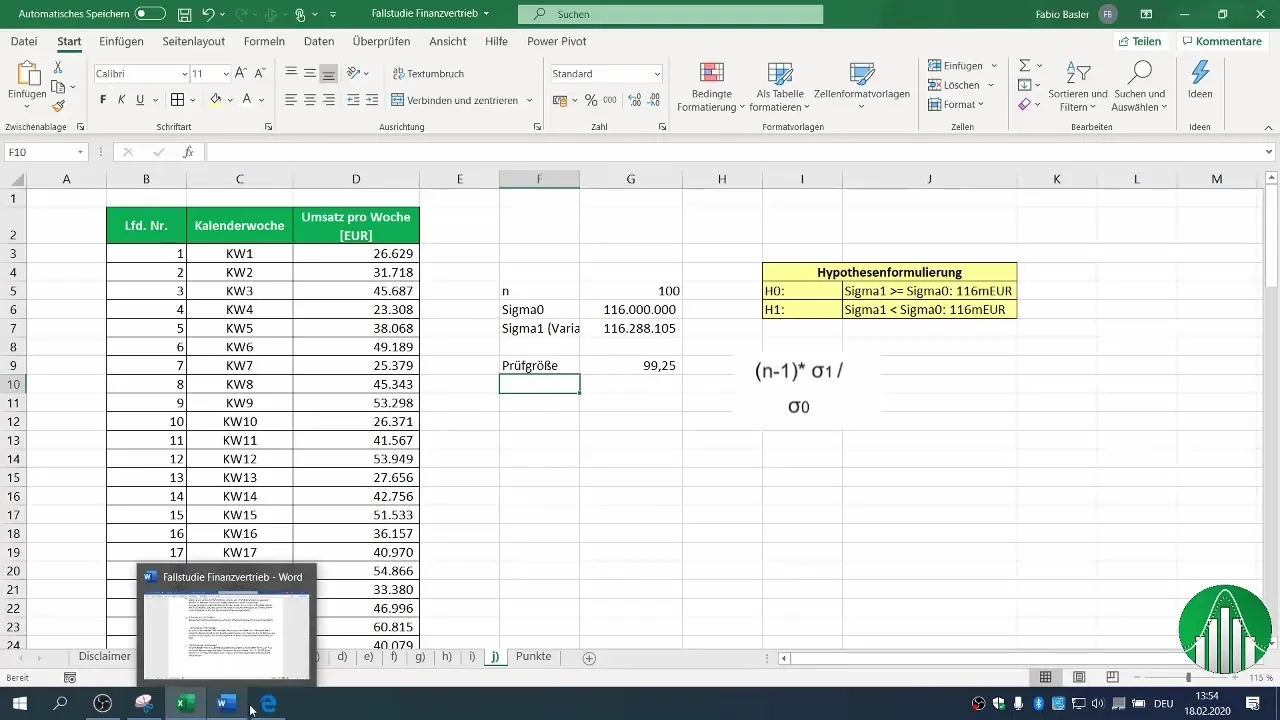
5. Prüfgröße kiszámítása
A Prüfgröße kiszámítható a minta szórása alapján. Végezd el a szükséges számításokat annak meghatározására, hogy mennyi lesz a Prüfgröße értéke. Ez a következő képlet alapján történik: (n-1) * σ1 / σ0, ahol σ1 a minta szórása és σ0 a múltból származó szórás.
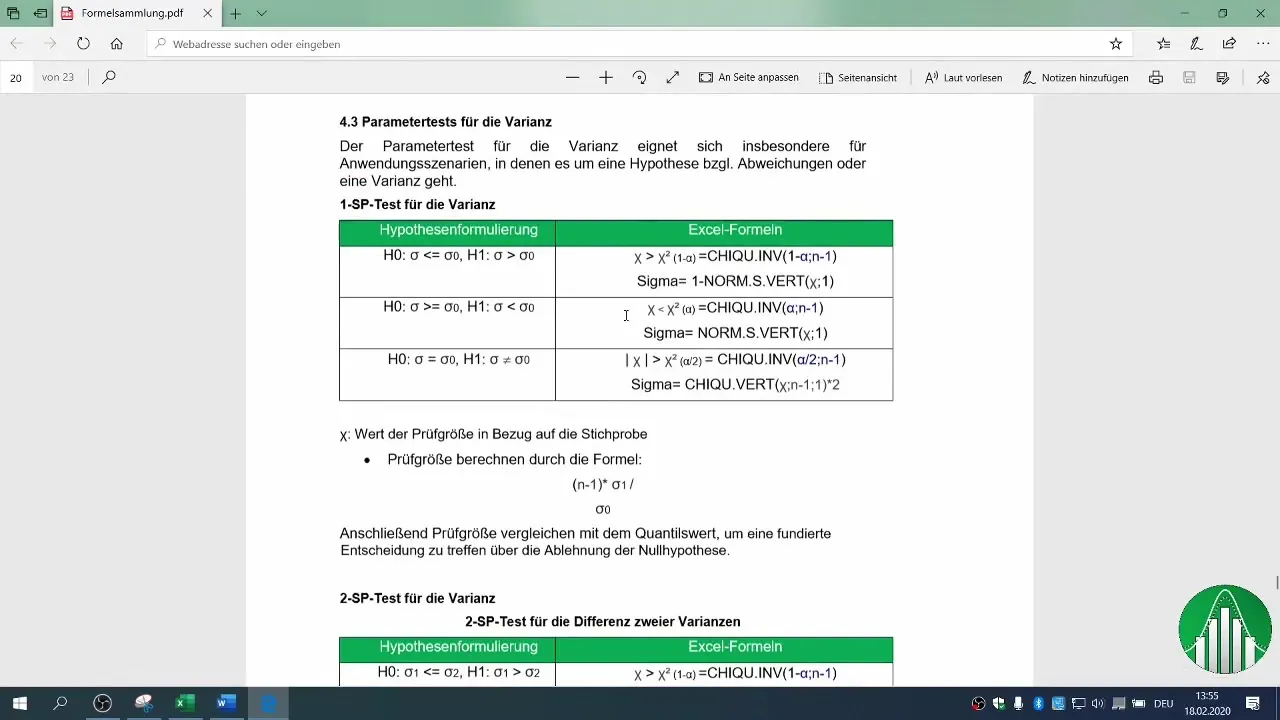
6. Kritikus tartomány meghatározása
Hogy eldöntsd, hogy elutasíthatod-e a nulla hipotézist, meghatározhatod a kritikus tartományt. Használd a Chi-négyzet-eloszlás táblázatot a megbízhatósági szintedhez. Ebben az esetben egy 2%-os hibaszám lehetőséget használtunk.
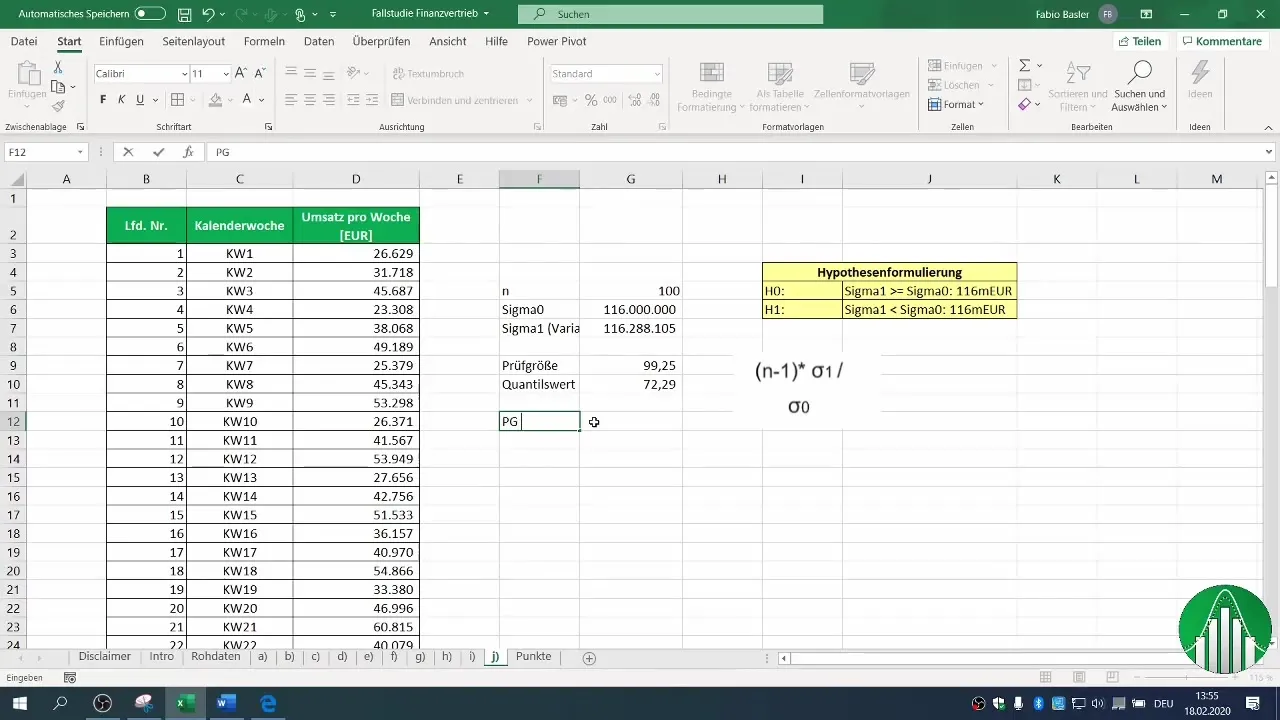
7. Prüfgröße és kritikus érték összehasonlítása
Vizsgáld meg most, hogy a kiszámított Prüfgröße érték kisebb-e, mint a kritikus érték. Ebben az esetben megállapítottuk, hogy a Prüfgröße értékünk nem kisebb, mint a kritikus kvantilérték.
8. Következtetések levonása
Az összehasonlítás alapján most eldöntheted, hogy elutasíthatod-e a nulla hipotézist vagy sem. Ebben az esetben arra következtettünk, hogy a nulla hipotézist nem lehet elutasítani. Ez arra utal, hogy az értékesítési adatok szórása továbbra is az elfogadott értéknek megfelelő vagy akár annál nagyobb.
Összefoglalás
Ebben az útmutatóban részletesen tárgyaltuk, hogyan végezhetsz Kétmintás-F-próbát Excelben. Megtanultad, hogyan készítsd elő az adataidat, hogyan fogalmazz hipotéziseket, számítsd ki a Prüfgröße-t, határozd meg a kritikus tartományt, és végül hogyan húzz következtetéseket. Ezekkel a lépésekkel fel vagy készülve, hogy önállóan végezz statisztikai elemzéseket.
Gyakran ismételt kérdések
Mi az a Kétmintás-F-próba?A Kétmintás-F-próba arra szolgál, hogy összehasonlítsa két adatcsoport szórását.
Hogyan fogalmazok hipotéziseket egy F-próbához?A nulla hipotézis szerint a szórás egyenlő vagy nagyobb, míg az alternatív hipotézis azt feltételezi, hogy a szórás csökkent.
Hogyan találom meg a kritikus értéket a próbámhoz?A kritikus értéket a Chi-négyzet táblázatok alapján állíthatod elő, a megbízhatósági szint és a szabadsági fokok függvényében.
Mit tegyek, ha nem utasíthatom el a nulla hipotézist?Ez azt jelenti, hogy az adatok megfelelnek az elfogadott szórásnak vagy akár nagyobb változatosságot mutatnak.
Szükségem van különleges szoftverre a próbához?A Kétmintás-F-próba elvégzéséhez elegendő az Excel, feltéve, hogy az adatok elő vannak készítve.

