Rangkorrelációs elemzések a változók közötti kapcsolatok statisztikai vizsgálatában kulcsfontosságúak. Különösen, amikor rangskálázott adatokról van szó, a Spearman-rangkorreláció értékes módszer a mintázatok és kapcsolatok felismerésére. Ebben a útmutatóban lépésről lépésre megtudhatod, hogyan számíthatod ki Spearman rangkorrelációját egy felméréshez Excel segítségével.
Legfontosabb megállapítások
- A rangkorreláció méri két rangskálázott változó közötti monoton kapcsolat erősségét és irányát.
- A Spearman ranggalapú korrelációs együttható különösen alkalmas, ha az egyik változó rangskálázott, a másik pedig metrikus skálázású.
- A számítás egyszerű képletek és funkciók segítségével történhet Excelben.
Lépésről lépésre útmutató
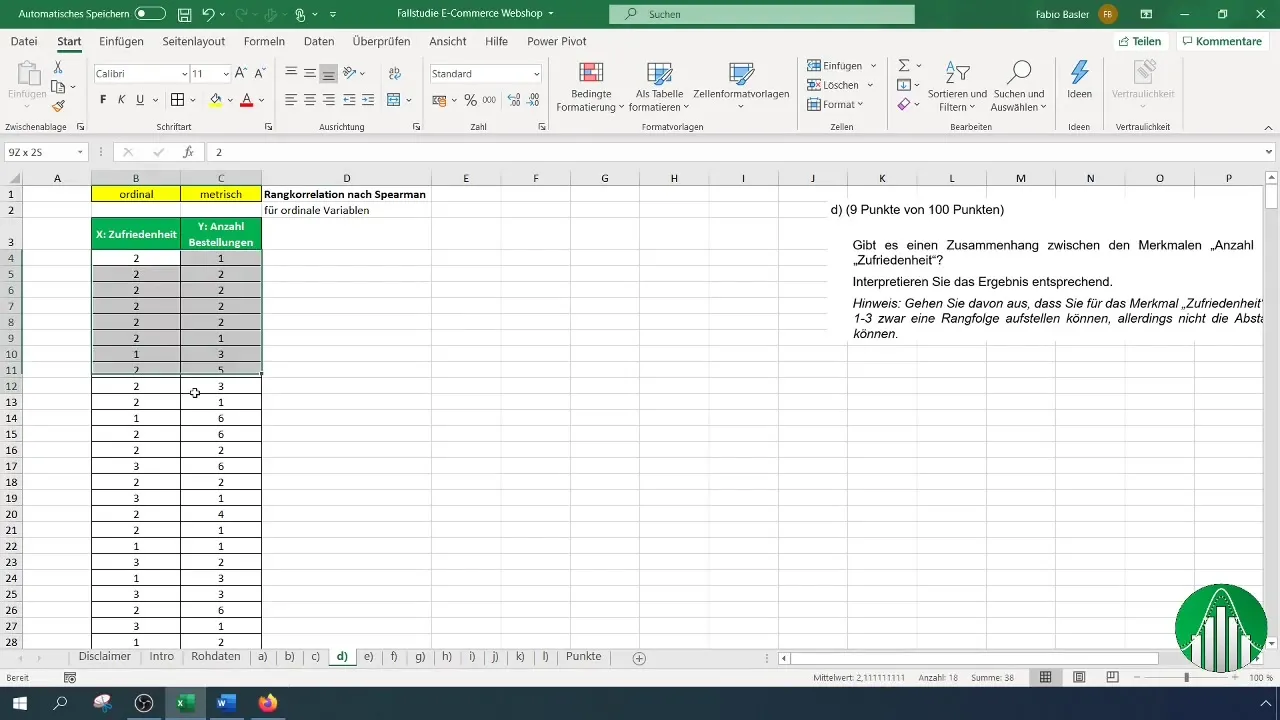
Először meghatározzuk azokat a változókat, amelyeket szeretnénk elemzni. Ebben az esetben a közönség megelégedettsége (rangskálázott, értékek 1-3) és a megrendelések száma (metrikus skálázott) a kérdéses.
A megelégedettség és a megrendelések rangsorolásához táblázatra van szükség, amely tartalmazza a megfelelő adatokat. Győződj meg róla, hogy ezeket az adatokat Excelbe írod.

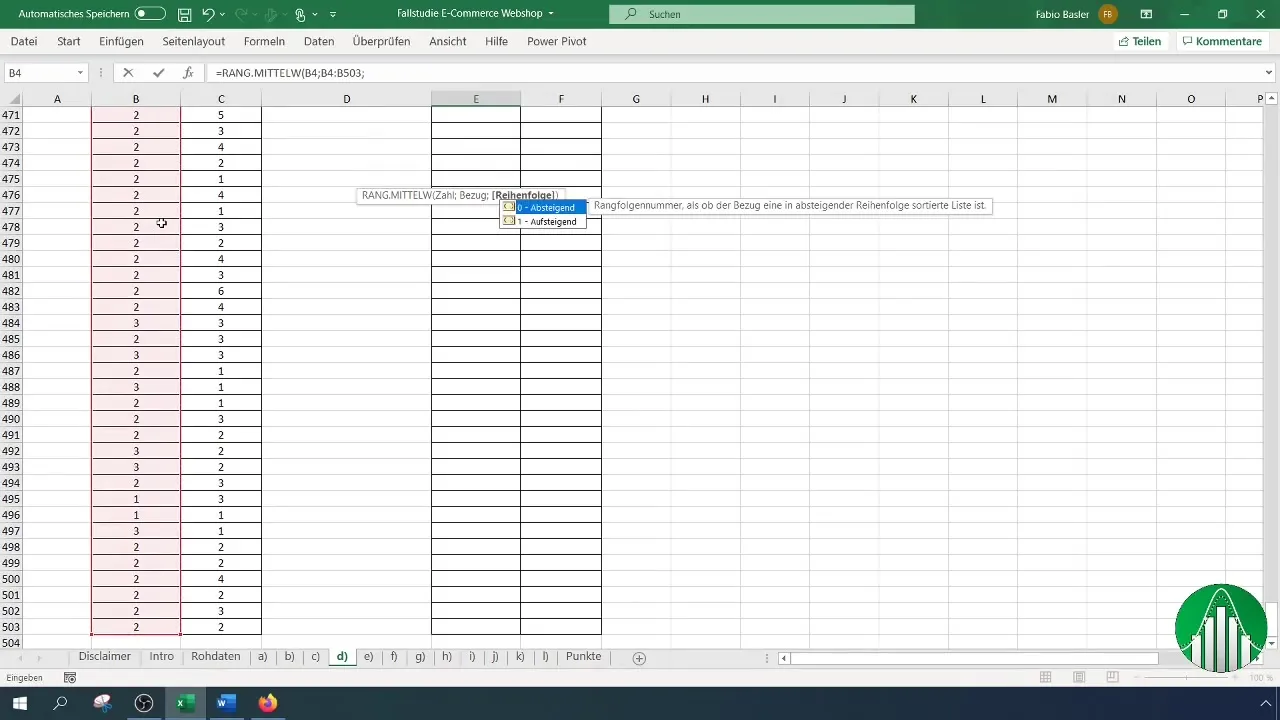
Amikor adataidat Excelbe beírtad, tekintsük meg a rangkorreláció számítását Spearman szerint. Ehhez az Excel „Rang.Közép” funkcióját használjuk, amely visszaadja egy szám rangját egy listán belül. A megelégedettséghez először ezt a képletet használjuk:
Emlékezz arra, hogy a képlet használatakor jelöld ki a megelégedettség oszlopát és állítsd be az adatsorod végejét B4-től, hogy a rangokat helyesen azonosítsd.
Ha meghatároztad a megelégedettség rangjait, ismételd meg ezt a folyamatot a megrendelések számára is. Győződj meg róla, hogy a képletet és a hivatkozást helyesen alkalmazod.
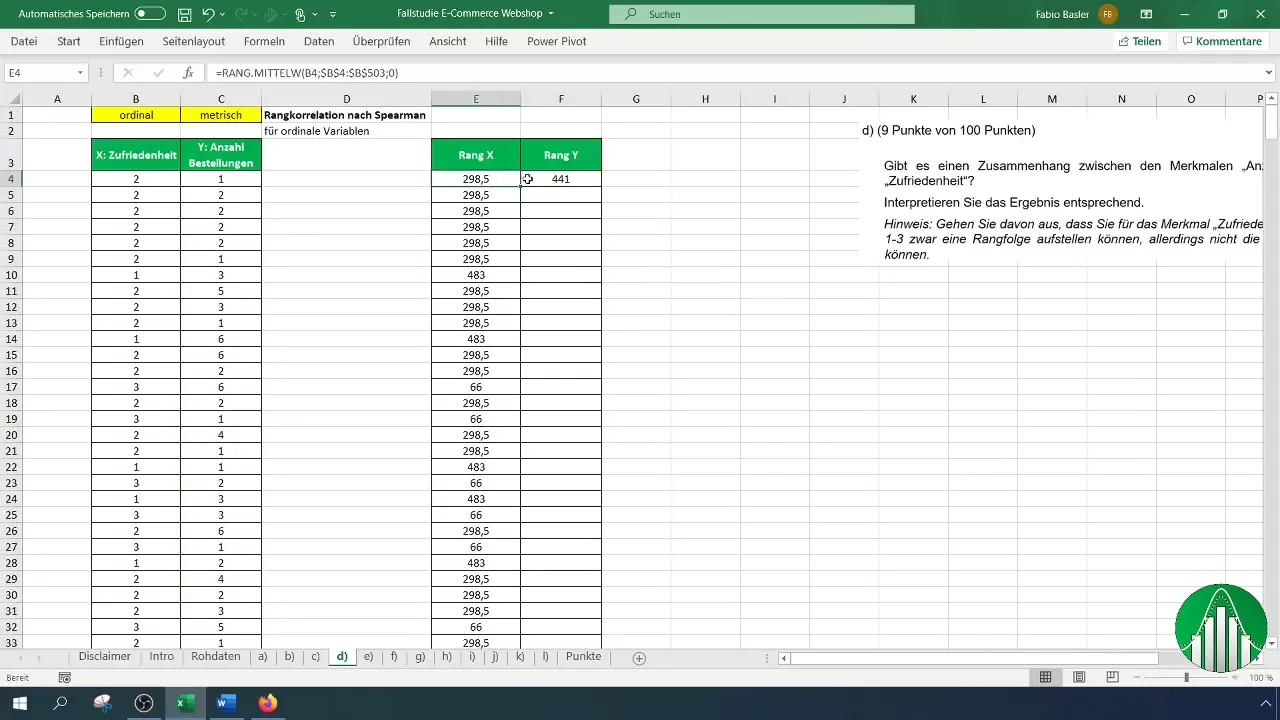
Miután megvannak mindkét rangsor (megelégedettség és megrendelések), készen állsz a Spearman rangkorrelációs együttható számítására. Ehhez használd az „=KORREL” képletet a kapcsolat meghatározásához. A szintaxis így néz ki:
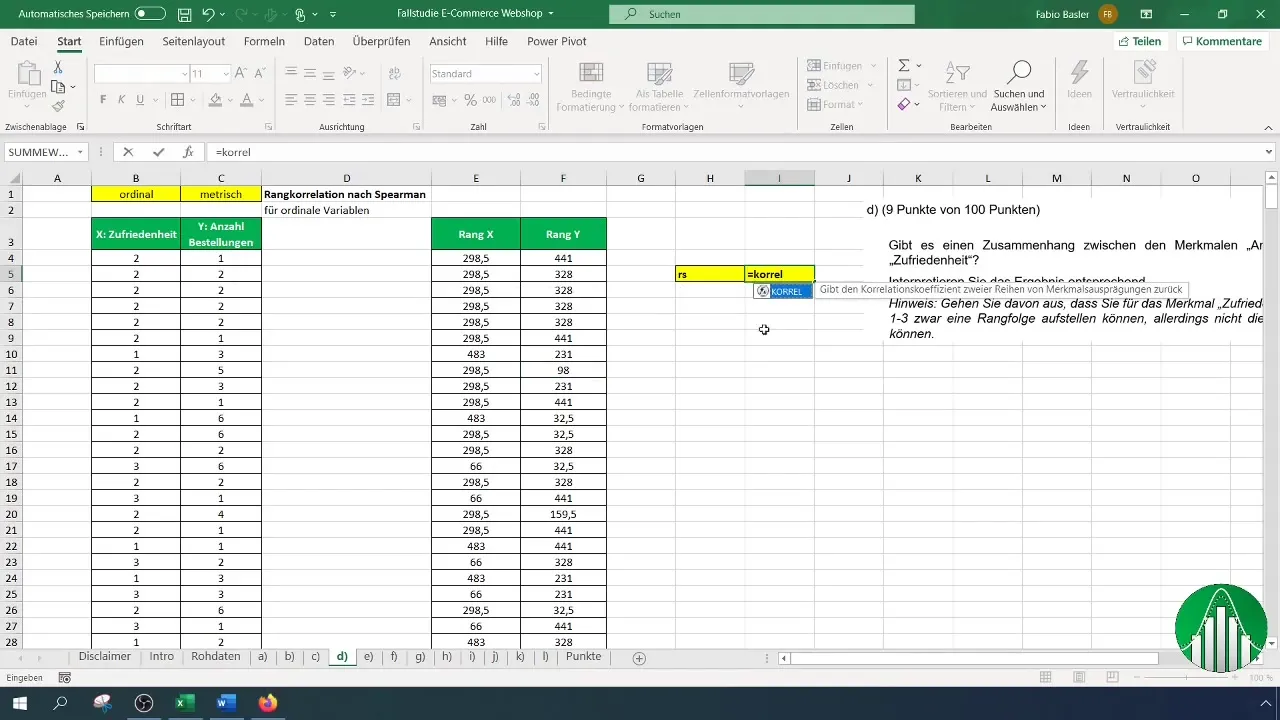
Az első hivatkozáshoz add meg a megelégedettség ranglistáját, a másodikhoz pedig a megrendelési ranglistát. Az Excel automatikusan kiszámítja a Spearman rangkorrelációs együtthatót.

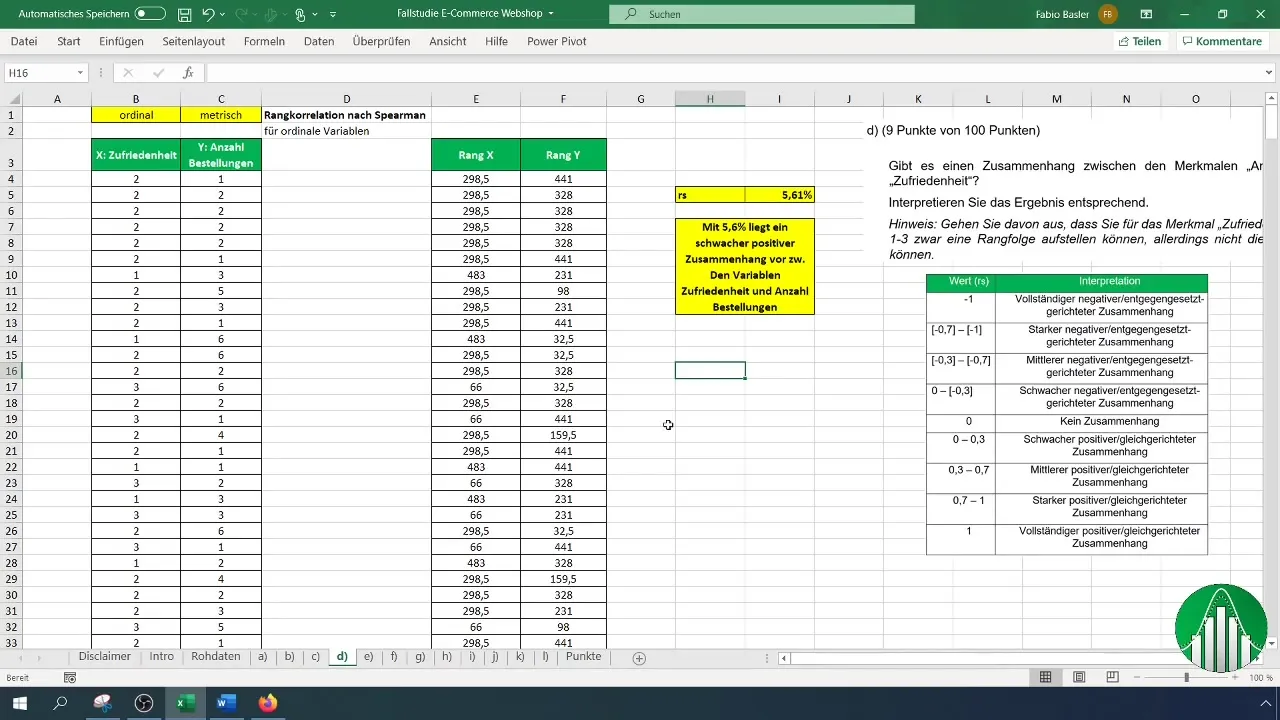
Mi az eredménye a számításodnak? Az 5,61%-os érték egy gyenge pozitív összefüggést mutat a megelégedettség és a megrendelések között. Ez azt jelenti, hogy szinte nincs jelentős kapcsolat ezek között a változók között.
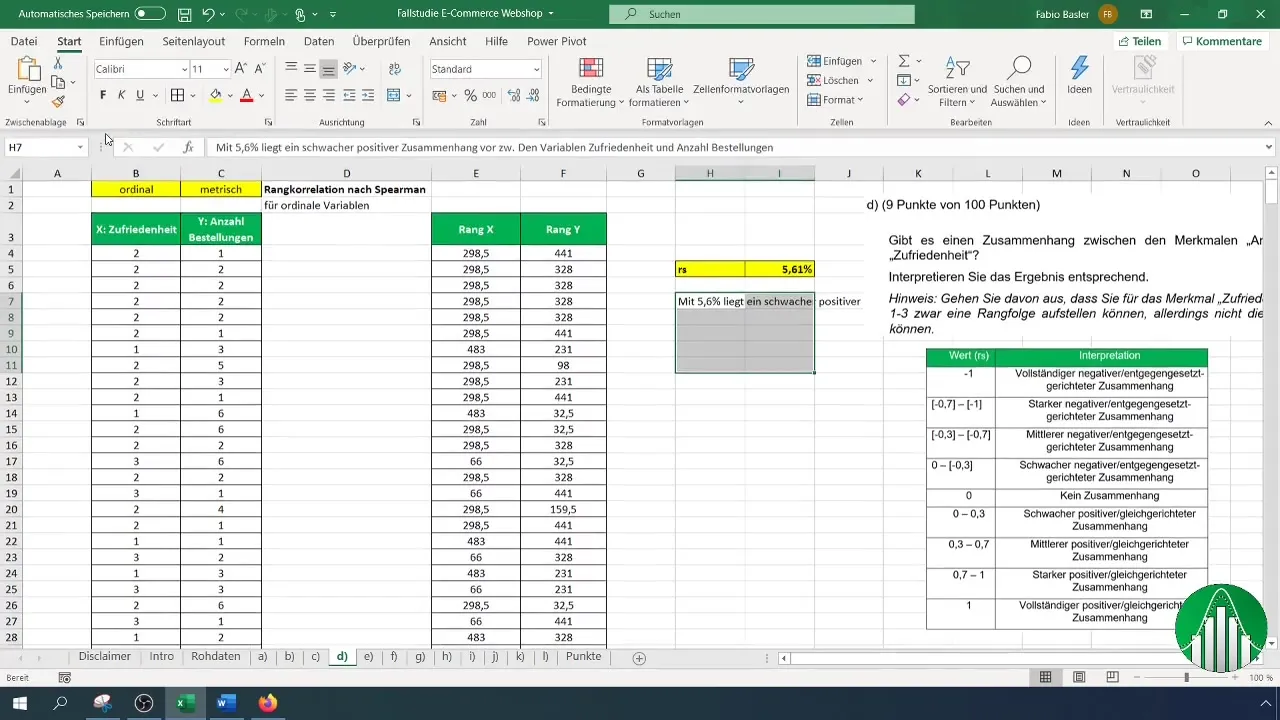
Az eredményeid értelmezéséhez használj egy értéktáblázatot, ahol felsorolják a rangkorreláció különböző tartományait. Az értelmezés után megerősítjük, hogy az alacsony korrelációs ráta azt jelenti, hogy a változók viszonylag függetlenek.
Összefoglalás
A Spearman rangkorreláció analízise Excelben lehetővé teszi, hogy értékes betekintést nyerj a rangskálázott és metrikus változók közötti kapcsolatokba. A módszer könnyen alkalmazható és világos nézetet biztosít a lehetséges kapcsolatokról.
Gyakran Ismételt Kérdések
Mi az a Spearman-rangsor korrelációs együttható?A Spearman-rangsor korrelációs együttható méri két változó monoton kapcsolatának erősségét és irányát.
Mikor érdemes a Spearman-együtthatót használni?Érdemes használni, ha legalább az egyik változó rangskálán van.
Hogyan számíthatom ki a Spearman-együtthatót Excelben?Használd a "Rang.Median" függvényt a rangok meghatározásához, majd a "KORREL" függvényt a kapcsolat számításához.
Milyen értéktartomány érvényes a Spearman-együtthatóra?Az együttható -1 és 1 közötti értékeket vehet fel. Az 1-hez közeli értékek erős pozitív korrelációt jeleznek, míg a -1-hez közeliek erős negatív korrelációt jeleznek.
Mit jelenthet egy 5,61%-os érték a rangkorrelációban?Az 5,61%-os érték gyenge pozitív összefüggést jelent, ami arra utal, hogy a változók viszonylag függetlenek egymástól.


