A Normális eloszlás a Valószínűségszámítás és Statisztika központi fogalma. Minden adatkészletben, amely egyenletesen eloszlik, észleljük a jellegzetes haranggörbét, amely gyakran előfordul felmérésekben és értékesítési elemzésekben. Ebben a bemutatóban megtanulod, hogyan számíthatod ki és vizualizálhatod az Excellel a Normális eloszlást egy felméréshez, hogy kiszámíthasd lényeges valószínűségeket. Ezekkel az készségekkel nem csak jobban megértheted az adataidat, hanem célzottan is felhasználhatod őket, hogy alapos döntéseket hozz.
Legfontosabb megállapítások
- El fogod sajátítani az Excelben a Normális eloszlás lépésről lépésre történő számítását.
- Bemutatásra kerül, hogy egy Normális eloszlás grafikus ábrázolása milyen lehetőségekkel jár.
- Meg fogod érteni, hogyan kalkulálhatók a konkrét események valószínűségei.
Lépésről lépésre történő útmutatás
Először bizonyosodj meg róla, hogy az összes szükséges adat egy Excel táblázatban rendelkezésre áll. Ezek az adatok például az egy felméréstől származó bevételeket reprezentálják.
A Normális eloszlás vizualizálása
Hogy a bevételek Normális eloszlását grafikusan megjelenítsd, kövesd az alábbi lépéseket:
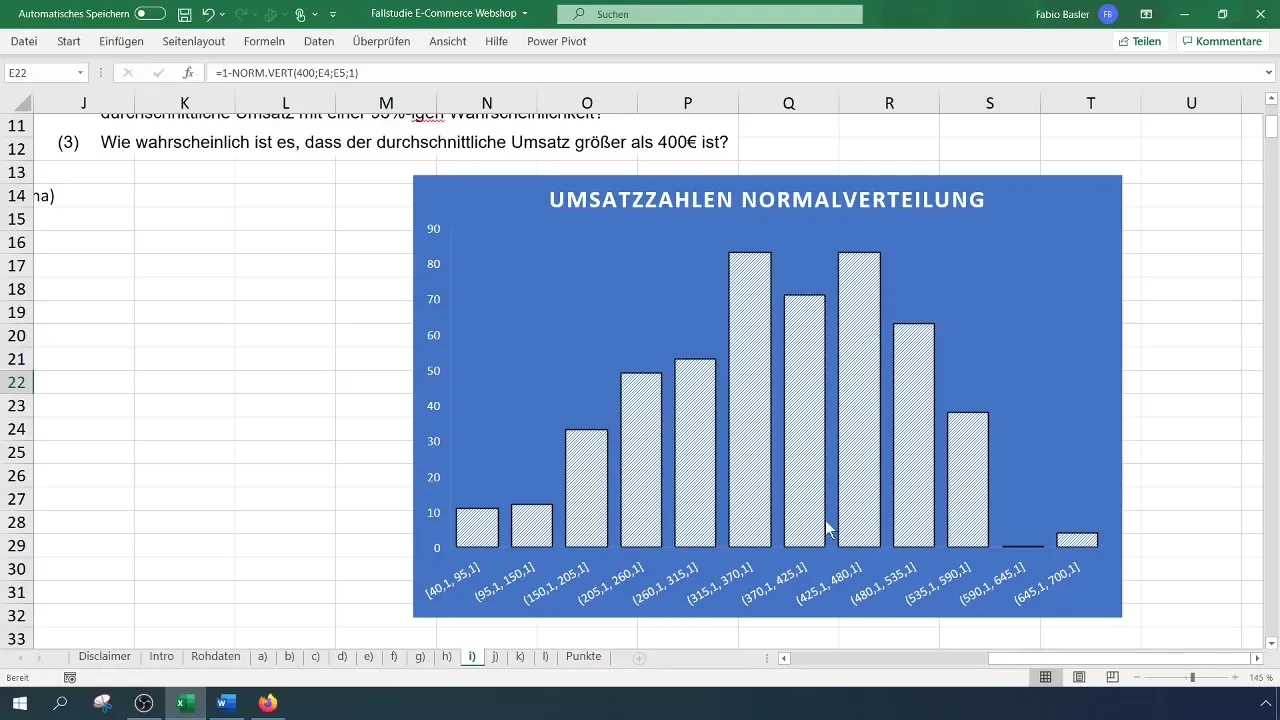
Először jelöld ki az Excel táblázatodban található bevételi adatokat, majd másold őket egy új oszlopba. A menüsorban kattints az "Beszúrás" lehetőségre, majd válaszd ki a "Diagramm" opciót. Itt válaszd a hisztogramot, hogy vizuálisan ábrázold az eloszlást. Választhatsz egy üres hisztogramot is, hogy az adataid alapértékeit megjelenítse.

A diagramon jobb gombbal kattints, majd válaszd ki az "Adatok kiválasztása" opciót. A megjelenő ablakban add hozzá az árbevétel adataidat az első adatsornak. Az értékek kiválasztásához tartsd lenyomva az Shift gombot és válaszd ki az értékeket.
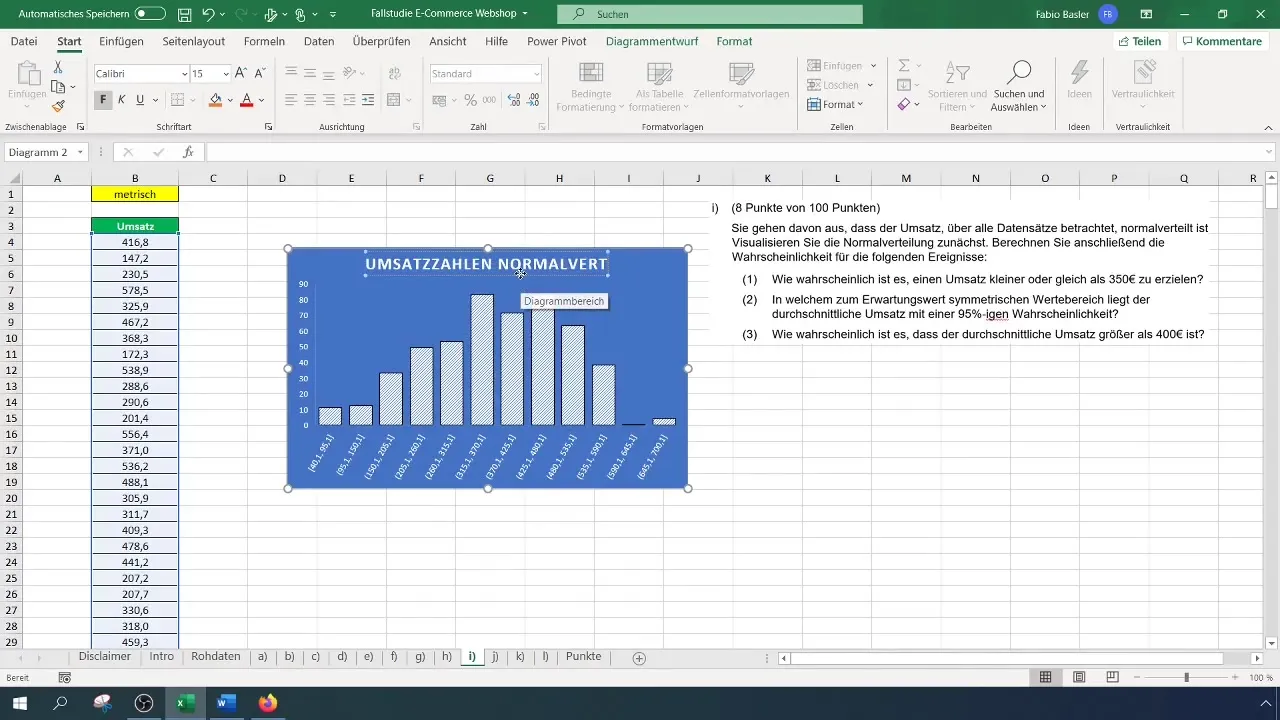
Amikor az adatok megjelennek a hisztogramon, módosíthatod a diagram címét, hogy reprezentatívabbá tedd. Például változtasd meg a címet "Bevételi adatok Normális eloszlása"-ra. Ügyelj arra, hogy a haranggörbe felismerhető legyen; ez a Normális eloszlásra utal.
Valószínűségek kiszámítása
A következő feladat az, hogy kiszámítsd annak a valószínűségét, hogy az árbevétel 350 eurónál kisebb vagy egyenlő lesz. Ehhez szükséged lesz az árbevételi adatok középértékére és szórása.
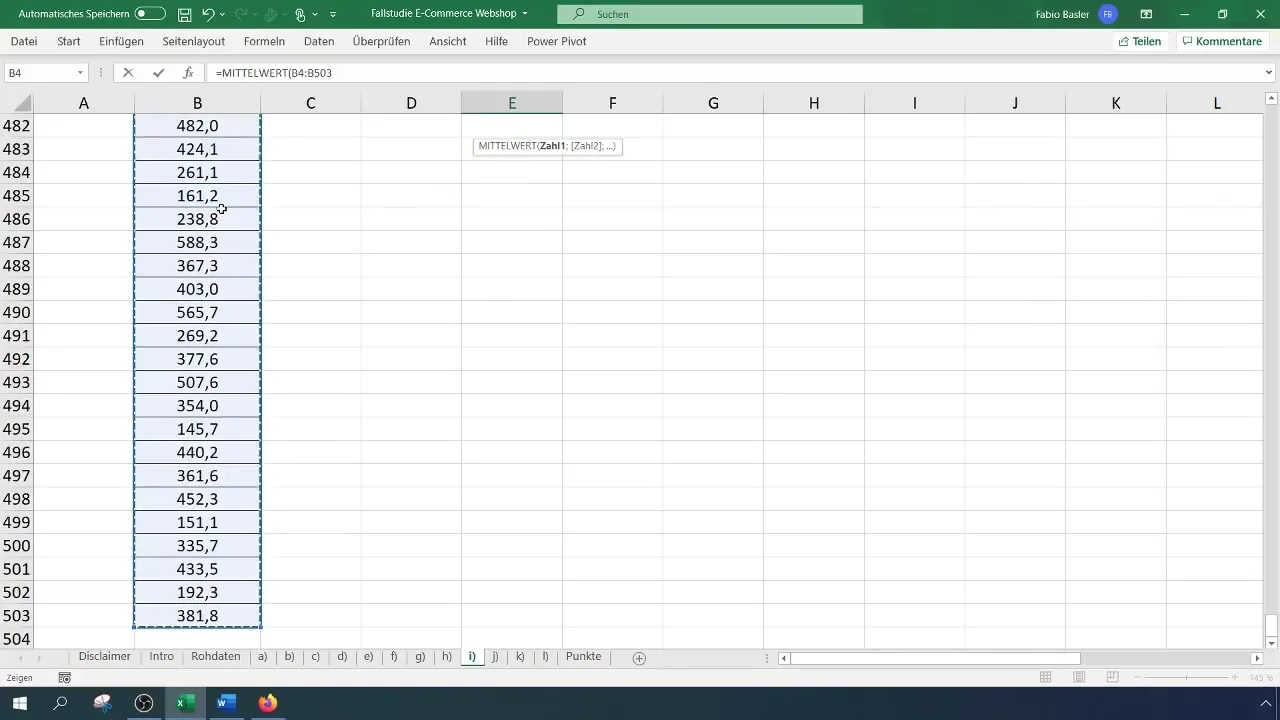
A középérték kiszámításához használhatod a következő képletet: =ÁTLAG(A1:A100) (Itt az A1:A100 az effektív adattartományt helyettesíti). Ebben az esetben például ez kb. 369 eurót eredményezhetne átlagos árbevételt.
A szórás kiszámításához használhatod a következő képletet: =SZÓRÁS.BEKSZINTELŰ(A1:A100), mely ebben az esetben kb. 124,12 eurót jelenthet.
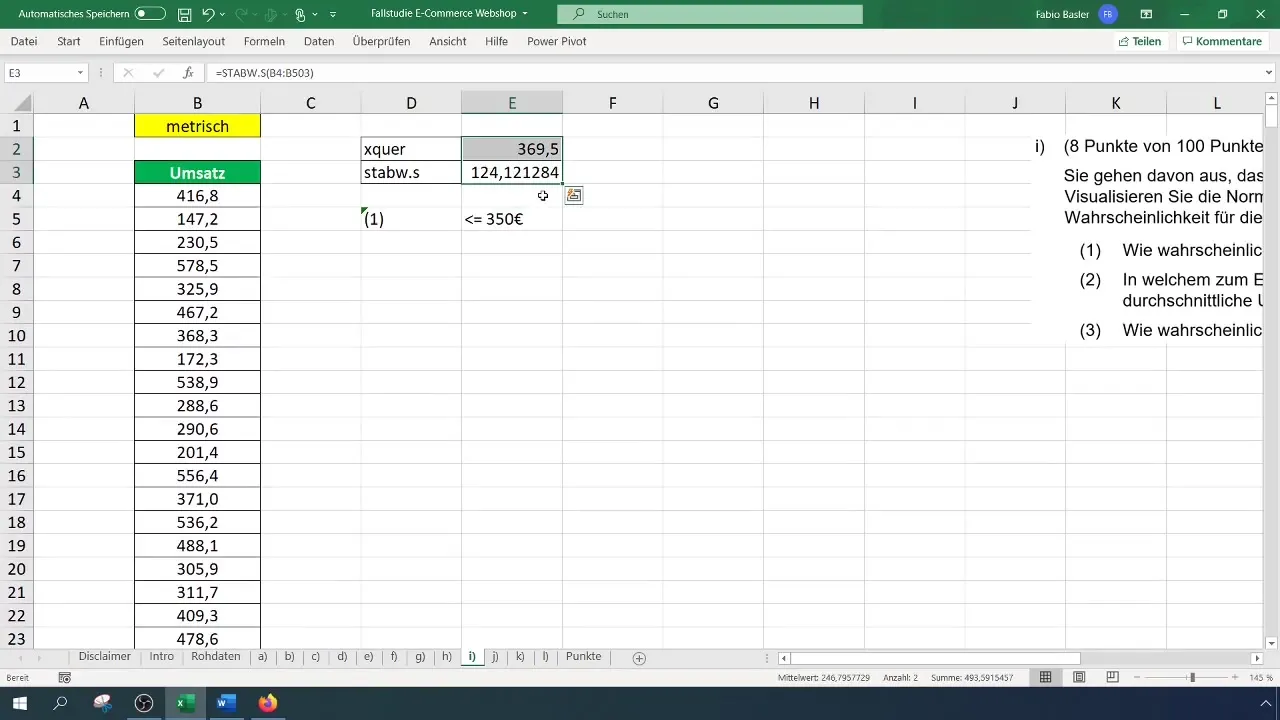
Most kiszámíthatod az egy 350 eurós árbevétel valószínűségét. Erre a következő képletet használd: =NORM.VERT(350; középérték; szórás; IGAZ). Illeszd be a megfelelő értékeket, majd nyomd meg az Enter billentyűt.
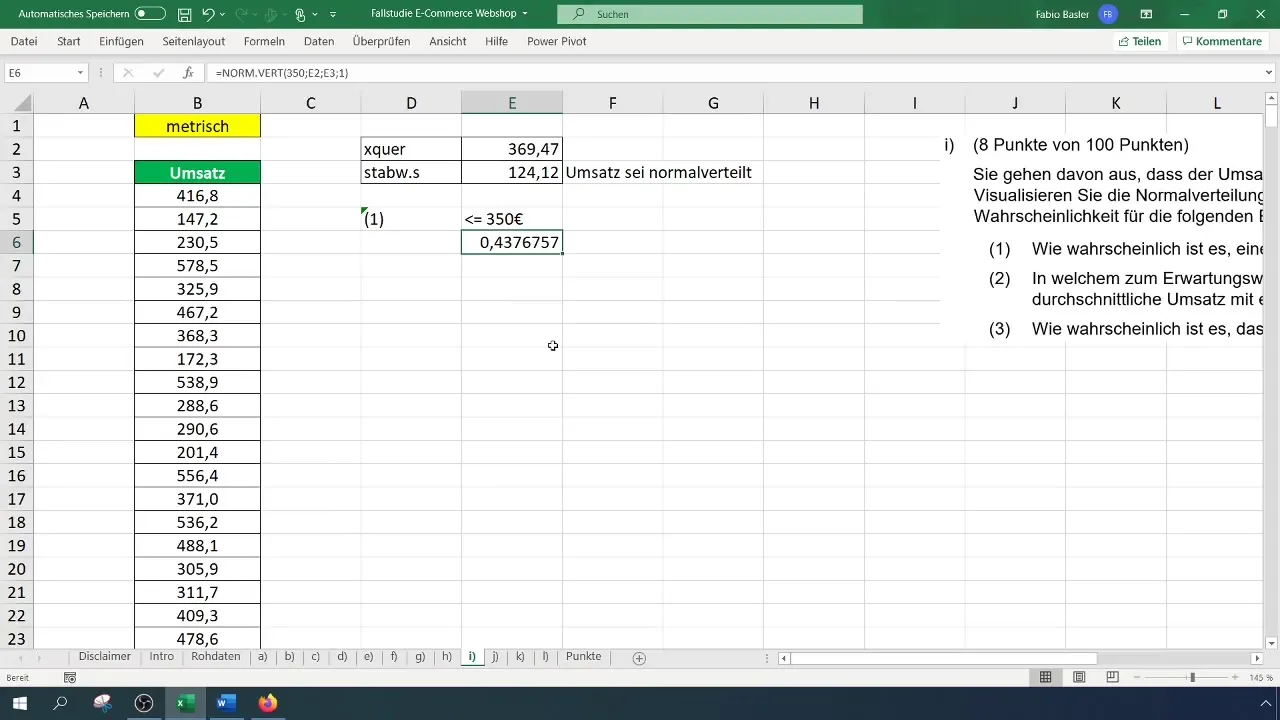
Ennek a számításnak az eredménye arra utalhat, hogy az árbevételnek 350 eurónál kisebb vagy egyenlő lenni valószínűsége nagyjából 43,8%. Hogy ezt szemléltessük, formázd át az értékeket, és állítsd be a százalékos megjelenítést.
Értékvártartomány kiszámítása az várható érték körül
A következő célpont az lenne, hogy kiszámítsd az értékvártartományt az várható érték körül 95% valószínűséggel. Ehhez meg kell határozni a kvantitatív értéket a 95%-hoz.
Ezt a következő képlettel teheted meg: =NORM.INVERZ(0,95) egy cellában, ami megadja a 1,65 kvantilis értéket.
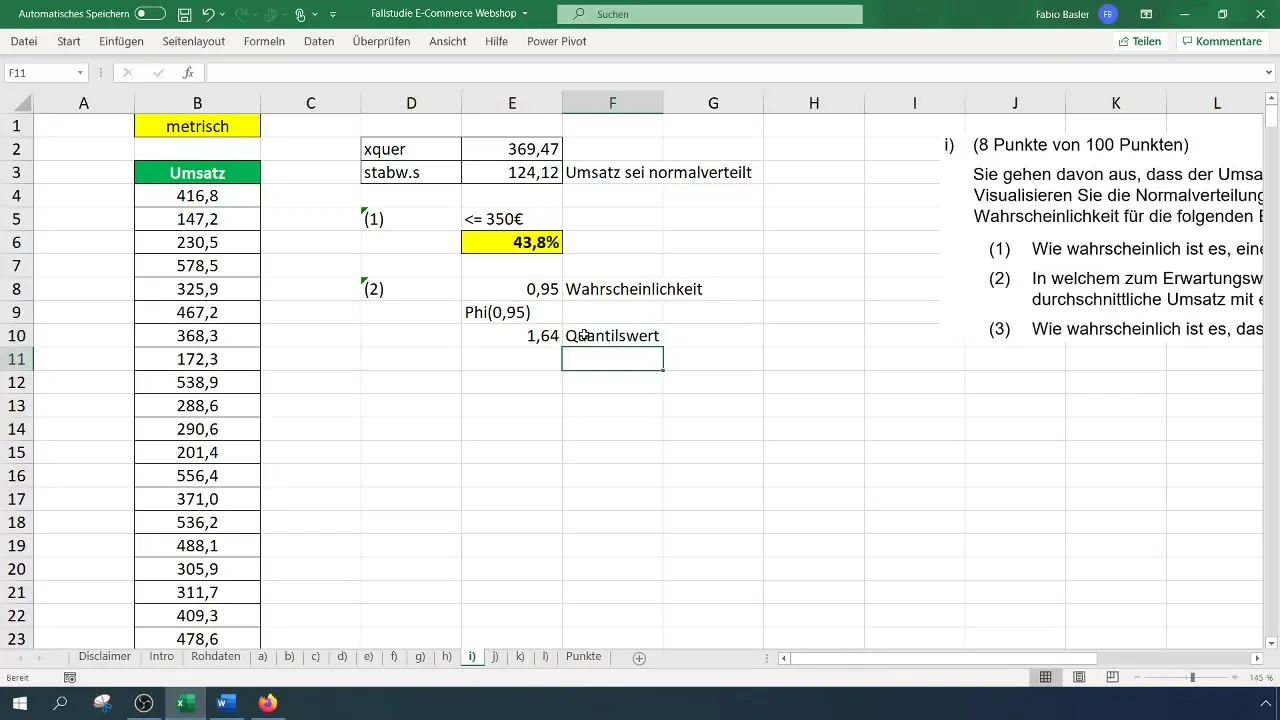
Ezt követően beillesztheted ezt a számítást egy egyenletbe, hogy megtaláld az értékvártartományt. A képlet lehetne például az alábbi: Várható érték + (Szórás * kvantilis érték). Illessz be a megfelelő értékeket, majd számold ki az értéktartományt.
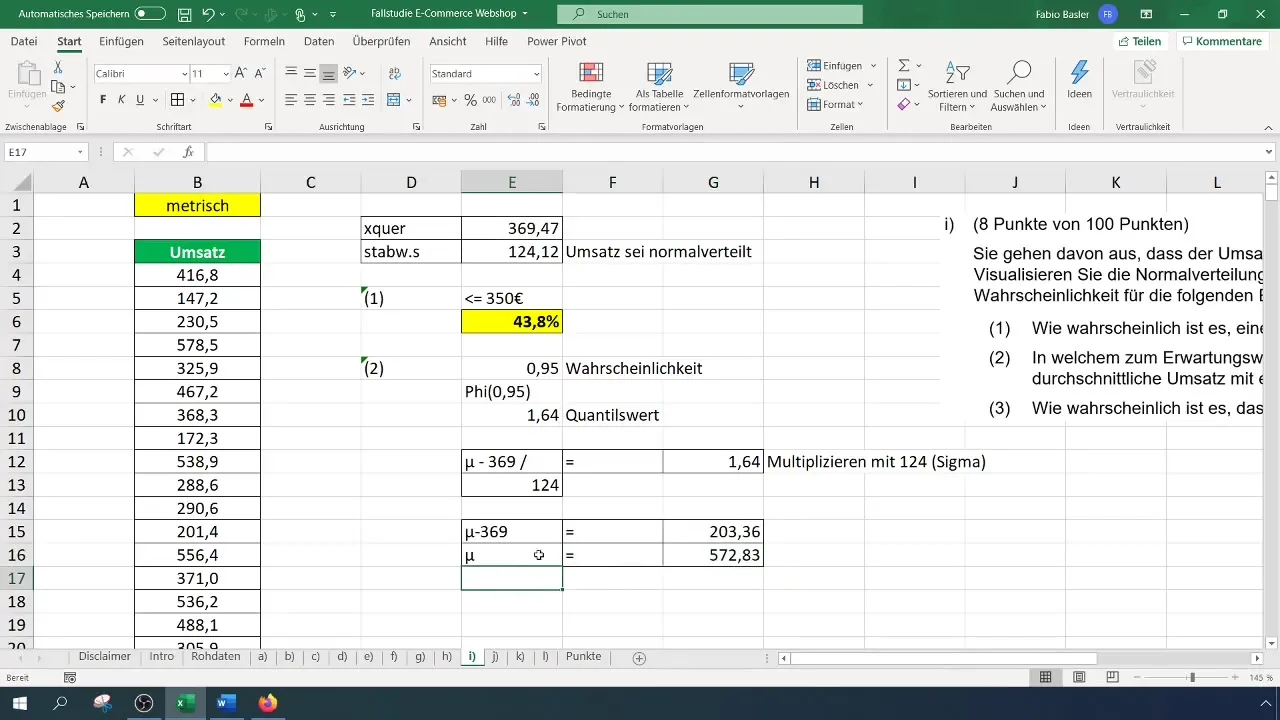
Például ha egy 572 eurós értéket kapsz, az azt jelenti, hogy 95% -os valószínűséggel várható egy forgalom ezen a tartományban.
Valószínűségek magasabb forgalmak esetén
Az utolsó számítás során a forgalom nagyobb lesz, mint 400 euróra számított valószínőséget fogod meghatározni. Ehhez használd a =1 - NORM.ELMÉL (400; átlag; szórás; IGAZ) formulát.
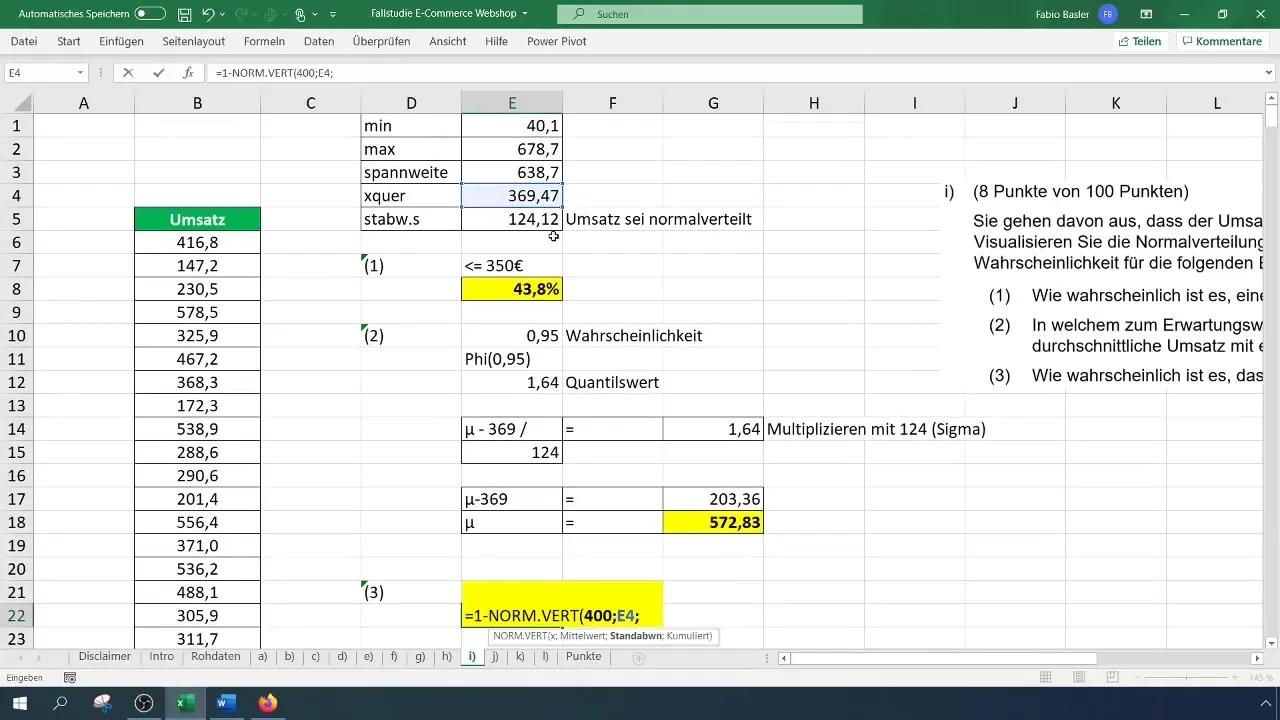
A valószínűség 40% -ra is emelkedhet. Ezeket az értékeket érdemes megkérdőjelezni. Amikor megtekinted a hisztogram skáláját, nyomon követheted a magasabb forgalmak arányának következetességét.
Összefoglalás
Ebben az útmutatóban megtanultad, hogyan használhatod az Excelt a valószínűségszámításra a normál eloszlás segítségével. Gyakorlati példákon keresztül megértetted, hogyan kezelheted az adatokat mind grafikusan, mind számításokkal. Ezeknek a fogalmaknak a megértése segíteni fog abban, hogy sikeresen végrehajtsd a statisztikai elemzéseket a projektedben.
Gyakran Ismételt Kérdések
Hogyan számíthatom ki a szórását Excelben?Használd a =SZÓRÁS.P(Dataterület) képletet a szórás számításához.
Használhatom a normál eloszlást nem normális adatokra?A normál eloszlás leginkább azokra az adatokra alkalmas, amelyek normálisan eloszlanak. Ellenkező esetben az eredmény félrevezető lehet.
Hogyan lehet testreszabni a grafikonokat Excelben?Kattints a diagramokra és válaszd ki a formázási lehetőségeket a felső menüsorban, hogy a diagramot az igényeid szerint testreszabhasd.


