A dátum elemzés területén kulcsfontosságú, hogy megalapozott döntéseket hozzunk, amelyek statisztikai hipotézisvizsgálatokon alapulnak. Ez az útmutató bemutatja, hogyan végezhetünk egyoldalú hipotézisvizsgálat t az arányérték számára az Excel segítségével. Egy példa segítségével, amely a Prémium vásárlók arányát vizsgálja, megtudhatod, hogyan végezheted el a lényeges statisztikai számításokat az Excelben, és hogyan alkalmazhatod ezeket az eredményeket hatékonyan.
Legfontosabb megállapítások
- Az egyoldalú arány értékének kiszámítása célszerű Excel alapú képletek segítségével történik.
- A hipotézisvizsgálatok lehetővé teszik a statisztikai elgondolások érvényességének ellenőrzését.
- Fontos, hogy a nullhipotézist és az alternatív hipotézist helyesen fogalmazzuk meg, hogy a megfelelő következtetéseket levonhassuk.
Lépésről lépésre útmutató
Az alapkérdés elemzése
A teszt kezdetén tisztázni kell az alapkérdést. A felmérésedből kiderült, hogy a Prémium vásárlók aránya 28 %. Meg szeretnéd tudni, hogy ez az érték jelentős mértékben növekedett-e azután, hogy különböző intézkedéseket tettek az ügyfélszerzés érdekében. Kezd el a feladatleírást a forrásból elolvasni.
Hipotézis bevezetése
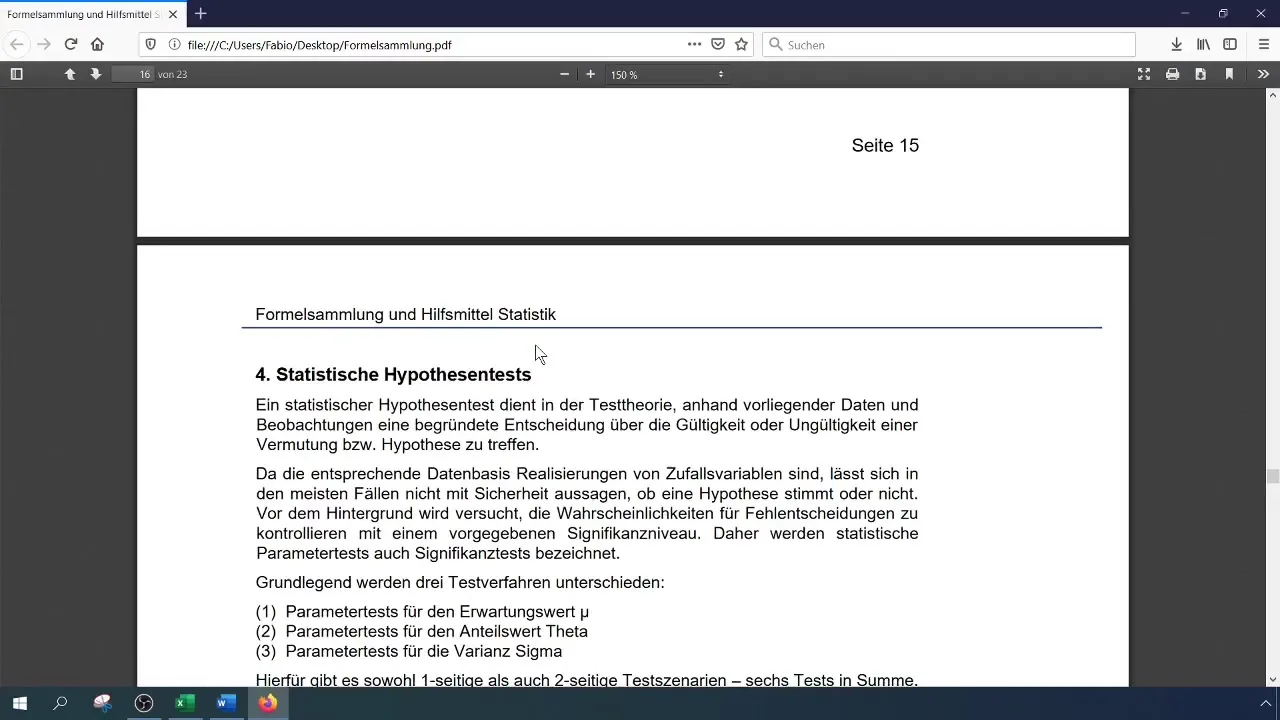
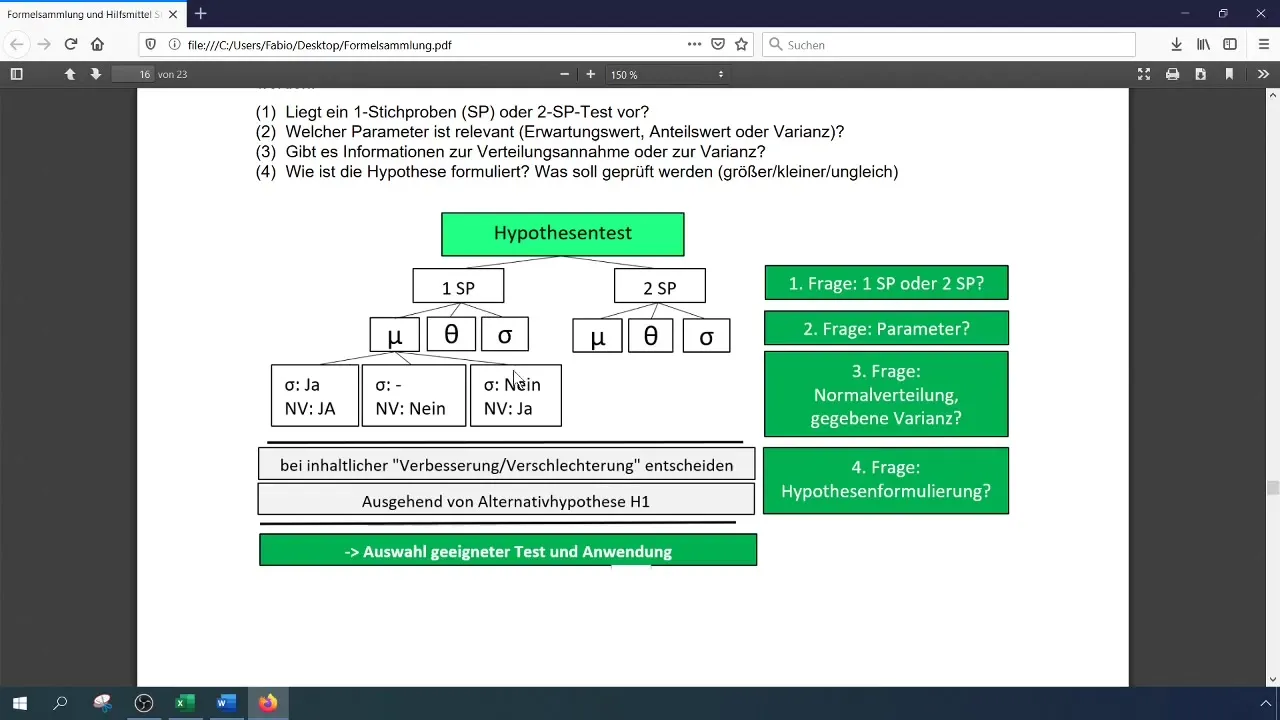
A statisztikai hipotézisvizsgálat segítségével döntéseket hozhatsz egy hipotézis érvényességéről. Megfogalmazod a nullhipotézist (H0) és az alternatív hipotézist (H1). Hagyományosan a nullhipotézis azt jelenti, hogy az aktuális arány értéke 0,28 marad, míg az H1 azt jelzi, hogy ez az érték nőtt.
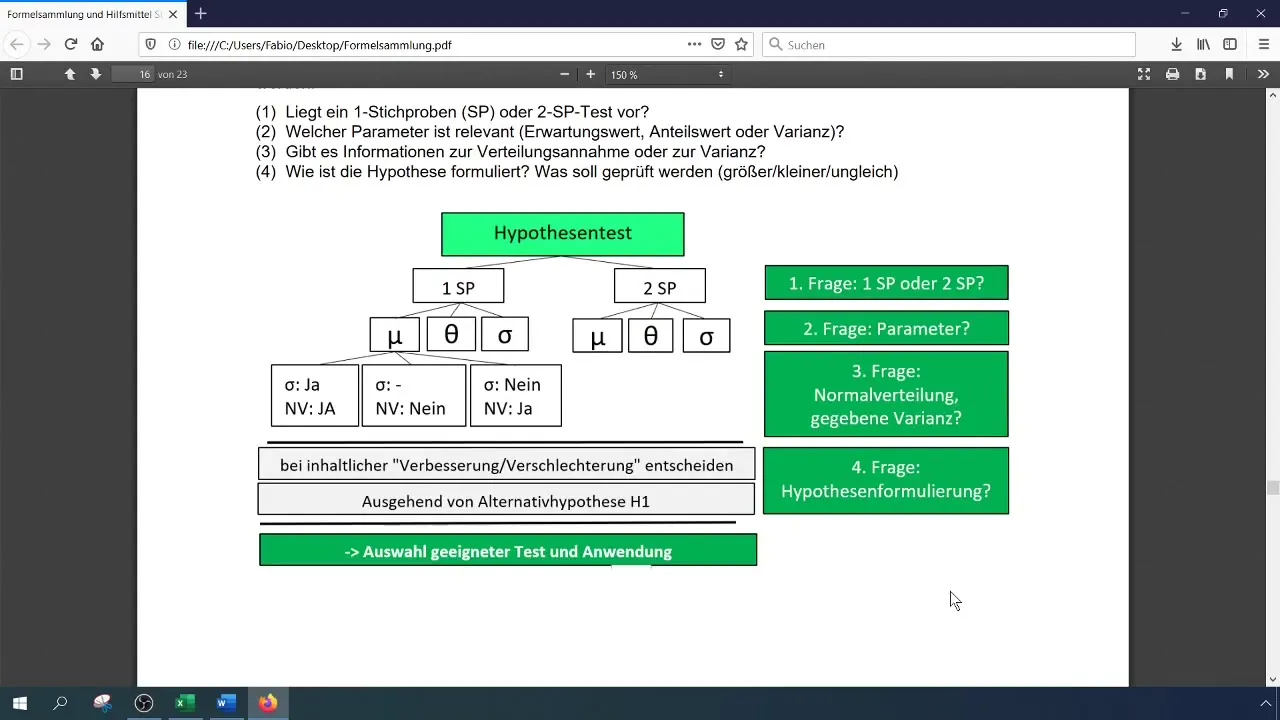
Formula és paraméterek tisztázása
Alapvető fontosságú a hipotézist világosan meghatározni:
- H0: θ ≤ 0,28
- H1: θ > 0,28 Ezzel az megközelítéssel egyértelműen meghatározhatod, mit szeretnél tesztelni.
Forrásadatok előkészítése
Mielőtt nekilátnál a számításoknak, elő kell készítened az eredeti adatokat. Ügyelj rá, hogy ne alkalmazz szűrőket az adatokra. Távolítsd el az összes szűrőt, hogy biztosítsd az összes adat teljes körű összegyűjtését.
Prémium vásárlók számolása
Most jön a Prémium vásárlók számának kiszámítása. Ezt az „HA” funkció segítségével tudod Excelben megtenni. A képlet használatához határozd meg a kiválasztási tartományt és a kritériumodat, ami a „Prémium” típusú.
Példaszámok megadása
A prémium vásárlók megszámolása után, amikor 164-et kaptál, kiszámíthatod, hogy ez az arány hogyan viszonyul a teljes vásárlói létszámban (500).
A vizsgálati statisztika kiszámítása
Számold ki a hipotézis standard hibáját. Használd az előzőleg megismert megközelítést a szórás meghatározására.
Hipotézisek tesztelése
Most érdekessé válik. Össze kell hasonlítanod a gép által generált vizsgálati számokat. Használj egy normális eloszlástáblát és határozd meg a kritikus értéket. Ebben az esetben az 5%-os kritikus érték 1,64.
Összehasonlítások és döntések
Most hasonlítsd össze a vizsgálati statisztikát a kritikus értékkel. Ha a vizsgálati statisztika nagyobb, mint a kritikus érték, akkor elutasíthatod a nullhipotézist. Egy 2,39-es eredmény itt nagyobb, mint 1,64, ami azt jelenti, hogy a Prémium vásárlók jelentősen növekedtek.
Eredmény végső ellenőrzése
Összefoglalva a teszted bizonyítja, hogy a Prémium vásárlók aránya nem csak a mintahalmazban nőtt, hanem az eredmények is átvihetők az alapnépességre.
Összefoglalás
Ebben a kézikönyvben megtanultad, hogyan végezheted el az egyoldalas hipotézisvizsgálatot az Excel segítségével az arányszám értékére. Az egész módszertan felkészít az hipotézisek megfogalmazására, a tesztstatisztikák kiszámítására és az eredmények értelmezésére. Mindig ügyelj arra, hogy az előtted álló teszteket mindig az ügyfelekre és az adatokra szabva értelmezd.
Gyakran Ismételt Kérdések
Hol találom a kritikus értéket a normális eloszlásban?A kritikus érték egy standard normális eloszlástáblázatban kereshető meg.
Mi történik, ha a tesztstatisztika kisebb a kritikus értéknél?Ebben az esetben nem tudod elutasítani a nullhipotézist, ez azt jelenti, hogy az hipotézis megcáfolható.


