Uji Statistik adalah bagian penting dari analisis data dan pengambilan keputusan. Terutama dalam bidang bioteknologi, dapat menjadi krusial untuk menguji hipotesis tentang tingkat keberhasilan dari bahan aktif. Dalam tutorial ini, Anda akan belajar bagaimana melakukan Uji Sampel Tunggal (1-SP-Test) untuk nilai harapan dengan varian yang diketahui secara efisien di Excel.
Temuan Utama
Panduan ini akan memberikan Anda:
- Dasar-dasar teoritis Uji Sampel Tunggal.
- Langkah-langkah untuk melakukan uji di Excel.
- Interpretasi hasil.
Persiapan Data
Untuk melakukan Uji Sampel Tunggal di Excel, Anda perlu data yang relevan terlebih dahulu. Dalam contoh kami, kami mengasumsikan situasi di mana Anda menganalisis tingkat keberhasilan bahan aktif. Diketahui bahwa tingkat keberhasilan rata-rata sebelumnya adalah 59%, dengan standar deviasi 19. Pertama-tama, Anda harus memasukkan data Anda ke dalam tabel Excel.
Pastikan data Anda diorganisir dalam kolom agar mudah diakses nantinya. Keteraturan yang baik akan membantu Anda untuk lebih mudah memahami langkah-langkah individual.
Ikhtisar Uji
Uji Sampel Tunggal digunakan untuk memeriksa apakah nilai harapan rata-rata berbeda secara signifikan dari nilai yang telah ditentukan. Dalam kasus ini, kita memeriksa apakah tingkat keberhasilan 59% dapat meningkat secara signifikan di masa depan.
Merumuskan Hipotesis
Hipotesis yang Anda buat untuk pengujian sangat penting:
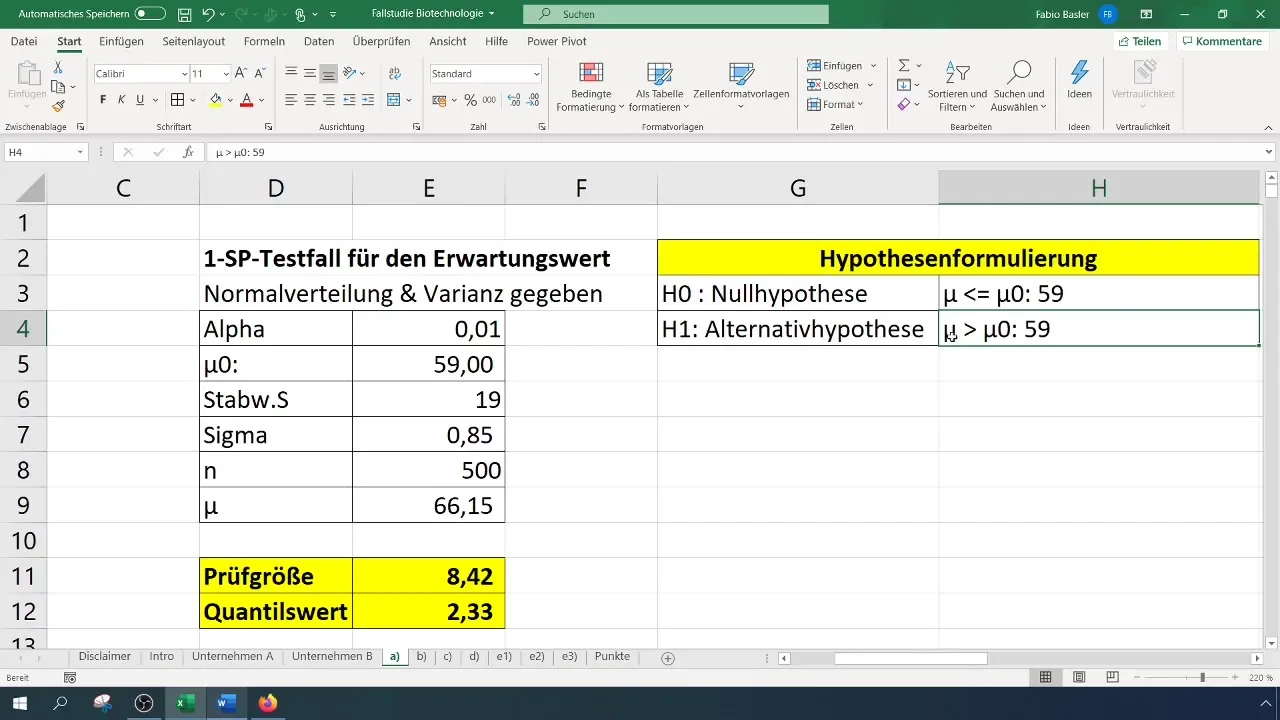
- Hipotesis Nol (H0): Nilai Harapan yang sesungguhnya sama dengan 59 (σ = 59%).
- Hipotesis Alternatif (H1): Nilai Harapan yang sesungguhnya lebih besar daripada 59%.
Saat merumuskan hipotesis, fokus pada apa yang perlu diuji dan bagaimana ini berdampak dalam konteks Anda.
Penting untuk memahami perbedaan antara Hipotesis Nol dan Hipotesis Alternatif dengan jelas, karena ini menjadi dasar untuk perhitungan selanjutnya.
Pengumpulan Sampel
Untuk uji kami, kami mengambil sampel dari 500 bahan aktif. Penting untuk memastikan bahwa pemilihan sampel representatif dan harus dijamin melalui metode yang sesuai agar hasil Anda bisa secara realistis diterapkan pada populasi secara keseluruhan.
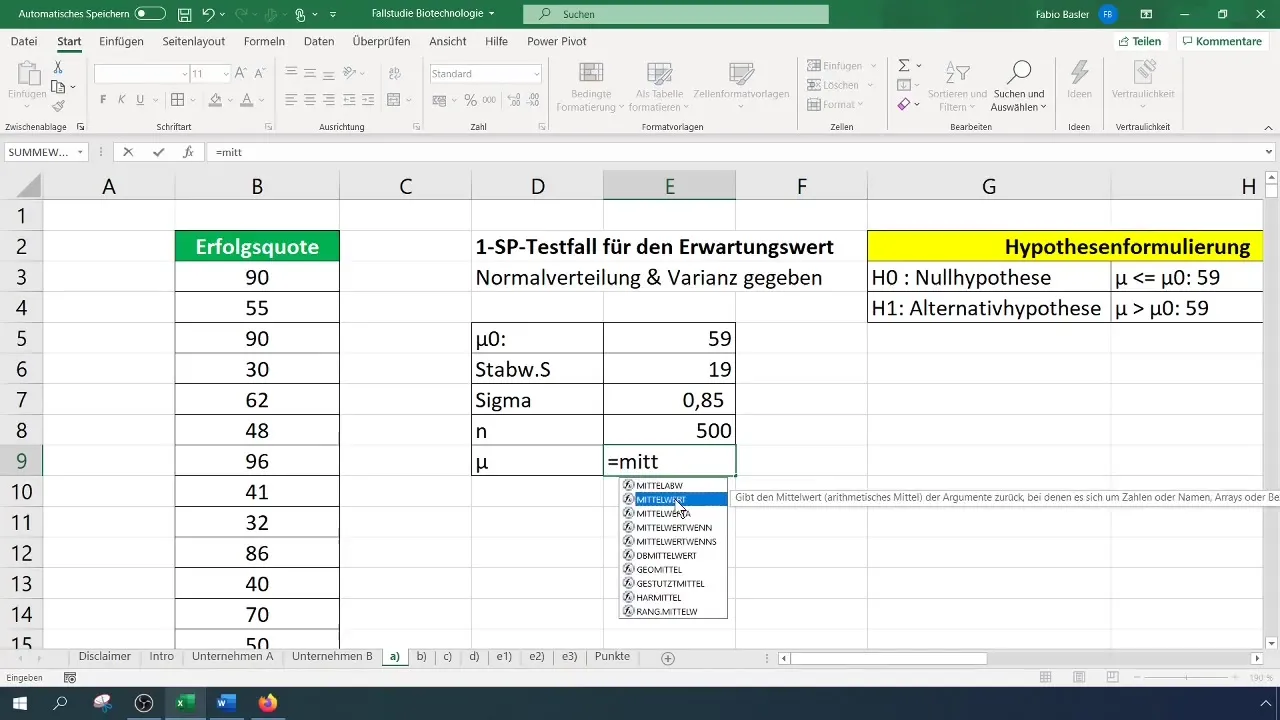
Untuk uji, pertama-tama hitunglah nilai rata-rata aritmatika. Ini harus dapat dilakukan dengan mudah dengan menggunakan rumus yang sesuai di Excel.
Perhitungan Ukuran Uji
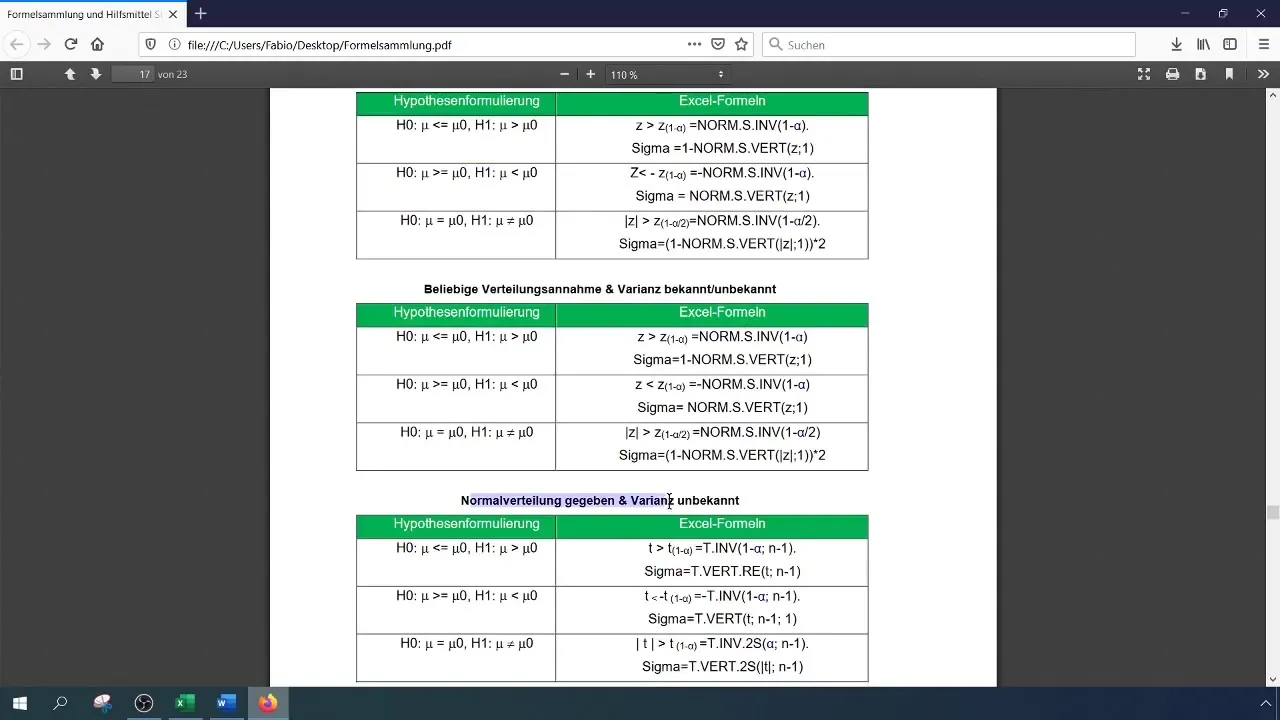
Ukuran uji untuk Uji Sampel Tunggal ditentukan oleh rumus berikut:
[ Z = \frac{\bar{x} - \mu_0}{\sigma/\sqrt{n}} ]
Di sini (\bar{x}) adalah nilai rata-rata sampel Anda, (\mu_0) adalah nilai rata-rata yang diasumsikan (dalam kasus ini 59), (\sigma) adalah standar deviasi (di sini 19), dan (n) adalah jumlah sampel (500).
Setelah Anda menyuntikkan nilai ke dalam rumus, hitung ukuran uji untuk menentukan apakah itu signifikan atau tidak.
Penentuan Nilai Kritis
Untuk tingkat signifikansi 1% (0,01), Anda perlu membaca atau menghitung nilai kritis. Anda bisa melakukan ini di Excel dengan menggunakan fungsi NORM.S.INV.
Rumusnya adalah:
[ \text{NORM.S.INV}(1 - \alpha) ]
Di sini (\alpha) adalah tingkat signifikansi (0,01). Nilai yang ditemukan akan menjadi dasar untuk membandingkan dengan ukuran uji.
Pelaksanaan Uji
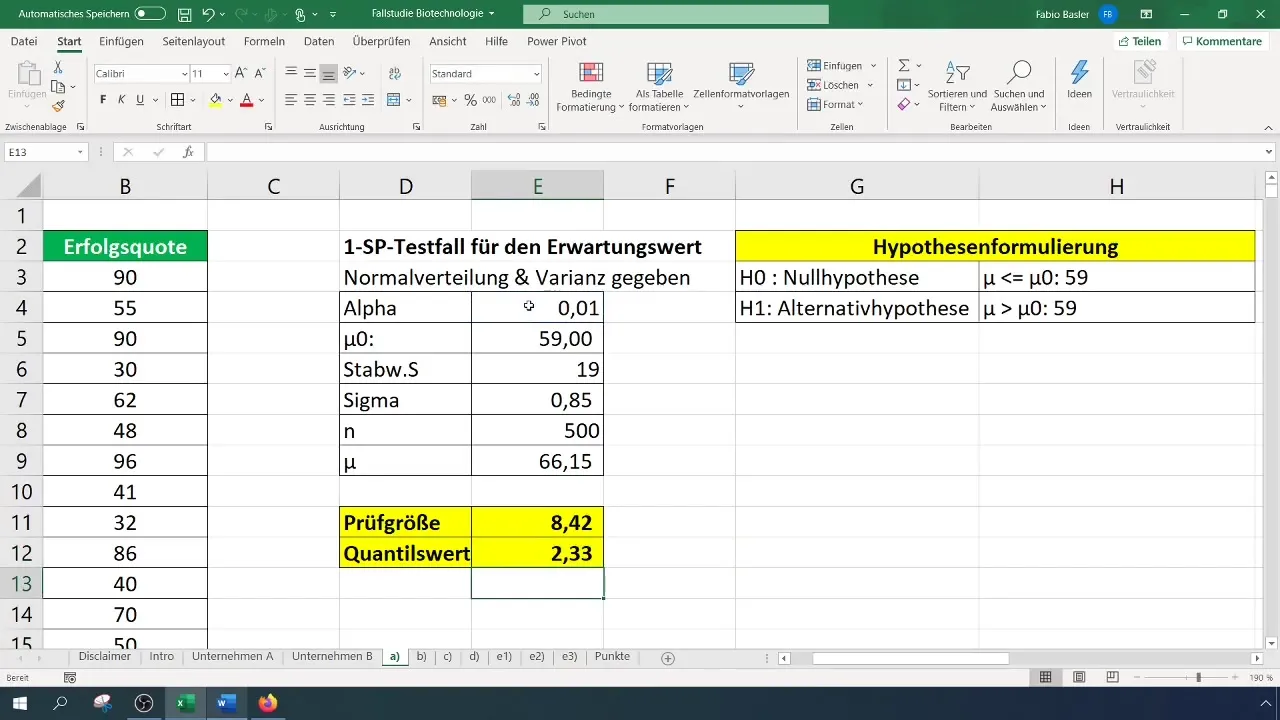
Setelah Anda memiliki ukuran uji dan nilai kritis, bandingkan keduanya:
- Jika ukuran uji lebih besar dari nilai kritis, hipotesis nol akan ditolak.
- Jika tidak, Anda tidak dapat menolak hipotesis nol.
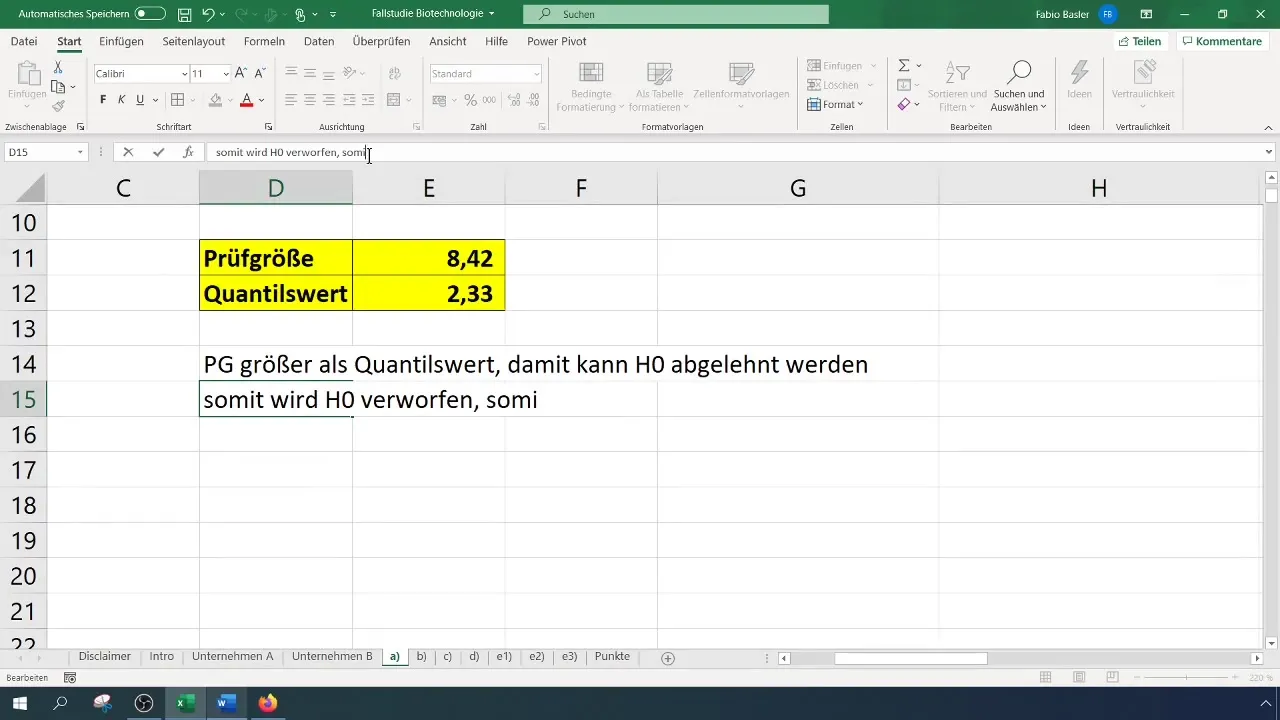
Dalam kasus kami, kami mendapatkan ukuran pengujian sebesar 8,4, yang melebihi nilai kritis sebesar 2,33. Oleh karena itu, kita dapat menolak hipotesis nol. Ini menunjukkan bahwa tingkat keberhasilan telah meningkat secara signifikan.
Interpretasi Hasil
Setelah melakukan uji dan mendapatkan hasilnya, Anda harus menginterpretasikannya dalam konteks yang jelas. Penolakan hipotesis nol berarti nilai baru yang diuji signifikan berbeda dari masa lalu, dalam hal ini 59%.
Informasi ini sangat penting untuk pengambilan keputusan strategis di perusahaan Anda. Mereka mengkonfirmasi bahwa upaya untuk meningkatkan tingkat keberhasilan telah berhasil.
Ringkasan
Dalam tutorial ini, Anda belajar cara melakukan uji 1-SP untuk nilai harapan di Excel. Melalui studi kasus, Anda dapat mengikuti langkah-langkah mulai dari merumuskan hipotesis hingga menghitung data hingga menginterpretasikan hasil. Pengetahuan ini tidak hanya berharga untuk evaluasi ilmiah, tetapi juga untuk aplikasi praktis di perusahaan.
Pertanyaan Umum
Apa itu uji 1-SP?Uji 1-SP adalah uji statistik untuk memeriksa apakah mean sampel berbeda secara signifikan dari nilai yang telah ditetapkan.
Bagaimana cara merumuskan hipotesis untuk uji?Hipotesis terdiri dari hipotesis nol (H0) dan hipotesis alternatif (H1) yang mendokumentasikan kondisi yang akan diuji.
Bagaimana cara menghitung ukuran uji?Ukuran uji ditentukan oleh rumus ( Z = \frac{\bar{x} - \mu_0}{\sigma/\sqrt{n}} ).
Apa yang terjadi jika ukuran uji lebih besar dari nilai kritis?Jika ukuran uji lebih besar dari nilai kritis, hipotesis nol akan ditolak.
Apa peran tingkat signifikansi dalam hal ini?Tingkat signifikansi menunjukkan seberapa besar kemungkinan Anda menerima kesalahan jika menolak hipotesis nol secara keliru.


