Dalam kerangka analisis statistik, pengujian hipotesis adalah salah satu instrumen utama yang memungkinkan Anda memeriksa berbagai asumsi tentang sekumpulan data. Dalam panduan ini, Anda akan belajar bagaimana melakukan pengujian sampel tunggal untuk varian di Excel. Anda akan mempelajari baik dasar-dasar teoritis maupun langkah-langkah praktis untuk menguji varian sampel Anda terhadap perubahan yang signifikan.
Temuan Utama
- Pengujian ini menguji apakah deviasi standar yang diketahui secara signifikan berbeda dari yang baru.
- Pengujian hipotesis untuk varian dilakukan melalui pendekatan sampel tunggal.
- Perhitungan melibatkan merumuskan hipotesis, menentukan ukuran uji, dan membandingkannya dengan nilai kritis dari distribusi Chi-Kuadrat.
Panduan Langkah Demi Langkah
Langkah 1: Persiapan Data
Pertama-tama, Anda perlu mengimpor atau memasukkan data Anda ke Excel. Data harus berisi nilai-nilai yang relevan untuk perhitungan varian. Untuk melakukannya, buka Excel dan buat tabel baru. Masukkan nilai-nilai ke dalam satu kolom.

Langkah 2: Menghitung Deviasi Standar dan Varian
Untuk menghitung varian, Anda perlu menggunakan deviasi standar dari sampel Anda. Jika Anda memiliki deviasi standar yang diketahui (dalam kasus ini 22), kuadratkan nilai tersebut untuk mendapatkan varian historis (σ0²). Gunakan rumus berikut:
Varian (σ0²) = (Deviasi Standar)²
Di Excel, Anda bisa langsung memasukkan rumus ini ke dalam sebuah sel.
Langkah 3: Merumuskan Hipotesis
Sekarang Anda akan merumuskan hipotesis nol (H0) dan hipotesis alternatif (H1). Hipotesis nol menyatakan bahwa varian sama dengan varian yang diketahui, sedangkan hipotesis alternatif menyatakan bahwa varian telah berkurang secara signifikan. Tulis sebagai berikut:
- H0: σ² = 484
- H1: σ² < 484
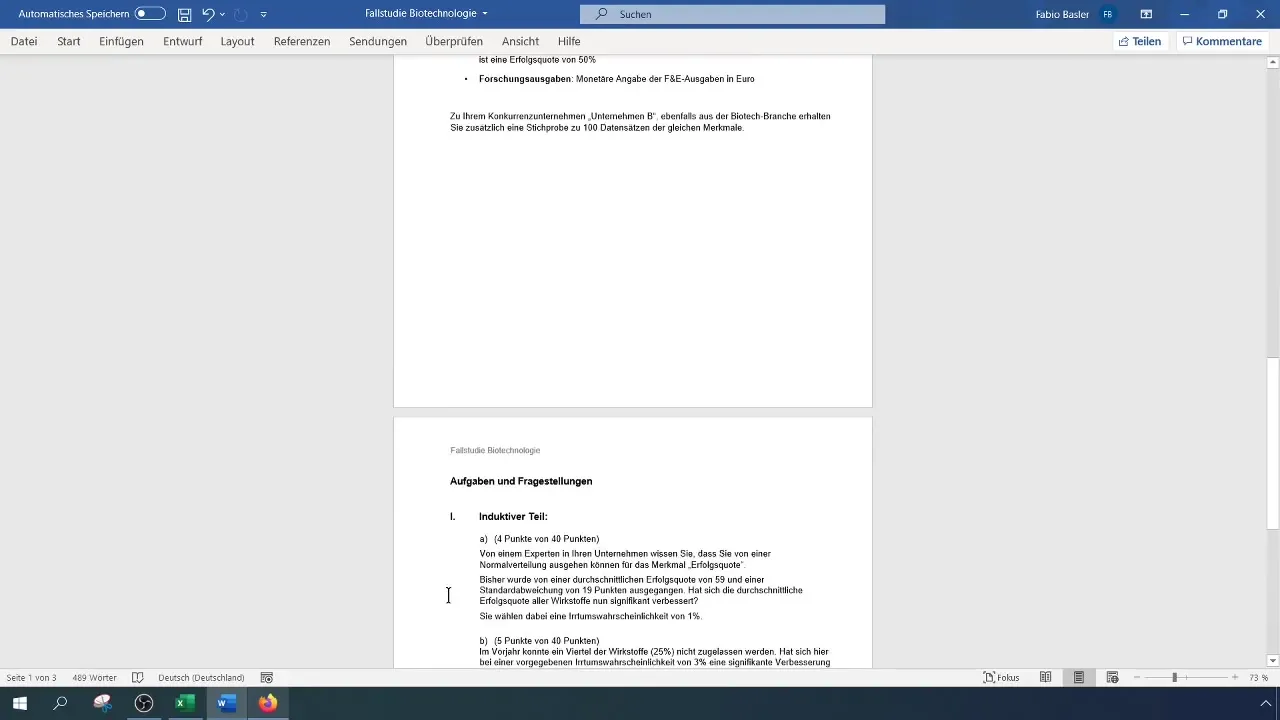
Langkah 4: Menghitung Ukuran Uji
Anda akan menghitung ukuran uji (χ²) dengan rumus berikut:
χ² = (n - 1) * (σ1² / σ0²)
Di sini, n adalah jumlah titik data dan σ1 adalah deviasi standar yang diestimasi dari sampel Anda. Untuk menghitung ini di Excel, Anda dapat merujuk ke sel yang sesuai.

Langkah 5: Menentukan Nilai Kritis
Untuk menemukan nilai kritis uji, Anda memerlukan distribusi Chi-Kuadrat. Anda bisa menghitung nilai ini di Excel dengan fungsi CHISQ.INV(), di mana Anda akan menggunakan tingkat signifikansi yang diinginkan (di sini 2,5% untuk uji satu arah) serta derajat kebebasan (n-1).
Langkah 6: Membandingkan Ukuran Uji dengan Nilai Kritis
Bandingkan sekarang ukuran uji yang dihitung (χ²) dengan nilai kritis. Jika ukuran uji lebih kecil dari nilai kritis, Anda dapat menolak H0. Ini berarti ada perbedaan yang signifikan dan varian telah berkurang.
Langkah 7: Menarik Kesimpulan
Berdasarkan pengujian Anda, Anda bisa merumuskan kesimpulan. Jika H0 ditolak, pastikan untuk menyatakan bahwa varian dalam populasi Anda secara signifikan lebih rendah dari varian awal. Dokumentasikan hasil Anda dan sampaikan dalam laporan.
Ringkasan
Dalam panduan ini, Anda telah belajar bagaimana melakukan pengujian sampel tunggal untuk varian di Excel. Dengan menerapkan dasar-dasar teori secara praktis, Anda akan dapat mendapatkan wawasan tentang data Anda.
Pertanyaan Umum
Bagaimana cara menghitung varian di Excel?Varian dapat dihitung di Excel dengan menggunakan rumus VAR.P() untuk populasi atau VAR.S() untuk sampel.
Apa perbedaan antara H0 dan H1?H0 adalah hipotesis nol yang mengasumsikan tidak adanya perbedaan. H1 adalah hipotesis alternatif yang mengasumsikan adanya perbedaan yang signifikan.
Apa yang harus dilakukan jika H0 tidak ditolak?Jika H0 tidak ditolak, ini berarti data tidak memberikan cukup bukti untuk menyatakan bahwa varian secara signifikan berbeda dari varian yang diketahui.


