Uji Kesesuaian Chi-Kuadrat adalah metode sederhana untuk memeriksa hipotesis apakah serangkaian data tertentu mengikuti distribusi normal. Dalam panduan ini, Anda akan belajar cara melakukan uji Chi-Kuadrat di Excel untuk memeriksa apakah penjualan ponsel pintar mengikuti distribusi normal. Kami akan membimbing Anda melalui proses langkah demi langkah, mulai dari pembuatan tabel frekuensi terklasifikasi hingga perhitungan ukuran uji dan perbandingan dengan nilai kritis Chi-Kuadrat.
Temuan Utama
- Uji Kesesuaian Chi-Kuadrat membantu dalam menguji distribusi normal.
- Membuat tabel frekuensi terklasifikasi adalah penting.
- Ukuran uji dibandingkan dengan nilai kritis untuk menolak atau menerima hipotesis nol.
Panduan Langkah Demi Langkah
Langkah 1: Menyiapkan Data
Untuk melakukan uji Chi-Kuadrat, Anda perlu data terlebih dahulu. Salin penjualan ponsel pintar ke lembar Excel. Pastikan data Anda diatur dalam satu kolom.

Langkah 2: Membuat Histogram
Untuk mendapatkan petunjuk visual awal tentang distribusi, buat histogram dari data Anda. Pergi ke "Sisip" dan pilih "Grafik". Tambahkan histogram dengan memilih rentang data.
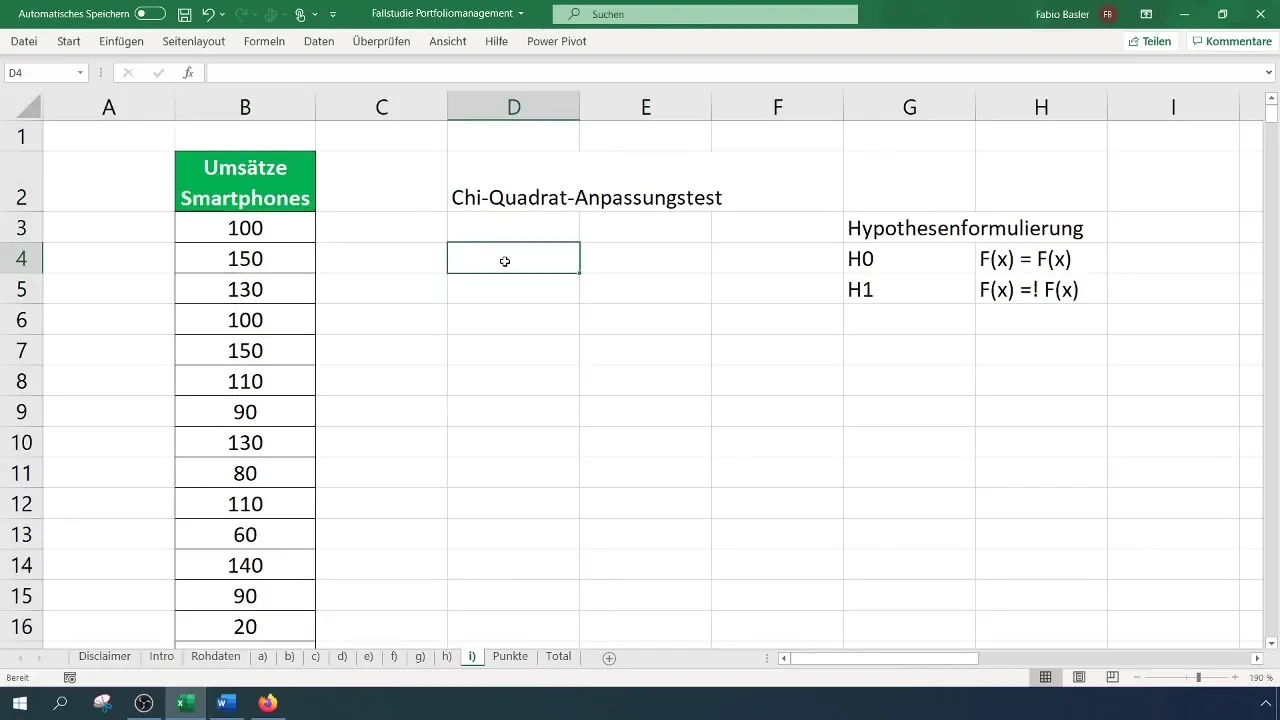
Langkah 3: Membuat Tabel Frekuensi Terklasifikasi
Untuk uji Chi-Kuadrat, Anda memerlukan tabel frekuensi terklasifikasi. Tentukan jumlah kelas untuk tabel Anda – dalam hal ini kita akan menggunakan enam kelas. Hitung lebar interval dan buat tabel sesuai.
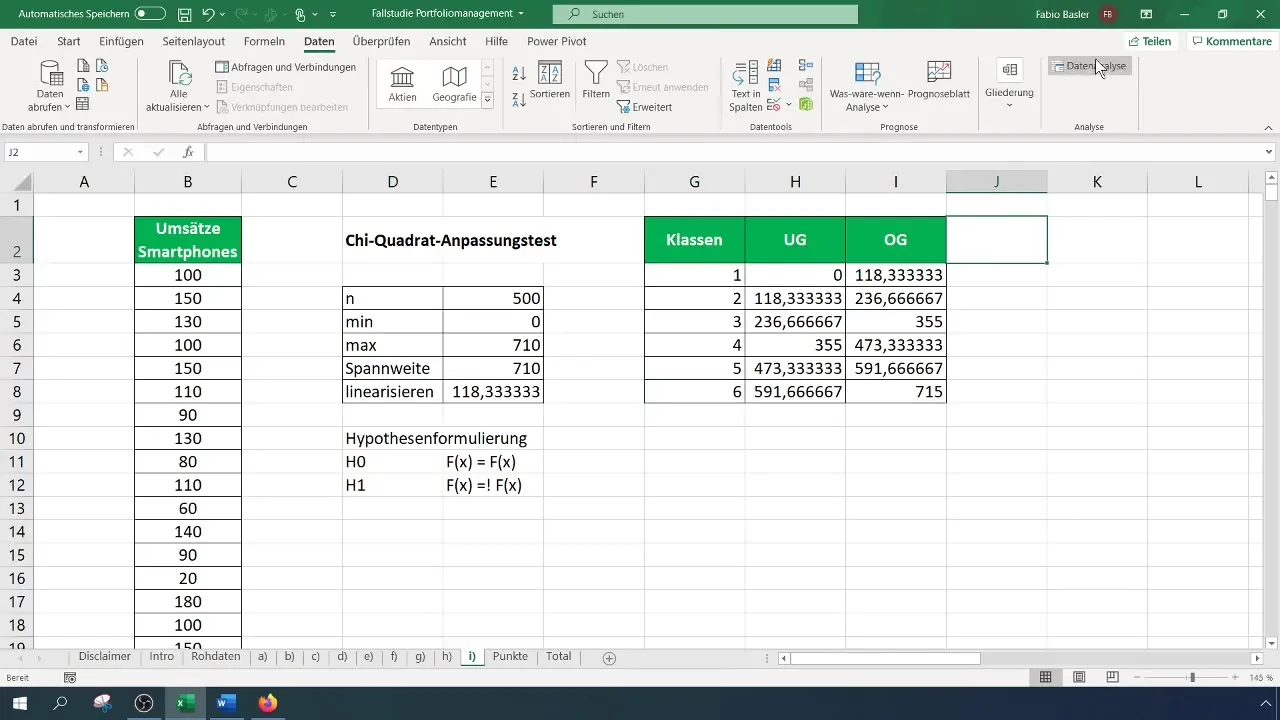
Langkah 4: Menghitung Frekuensi
Sekarang Anda harus menghitung frekuensi yang diamati untuk setiap kelas. Pergi ke "Analisis Data" dari menu dan pilih "Histogram". Pilih rentang input untuk data Anda dan batas kelas. Tentukan rentang output untuk tabel frekuensi.
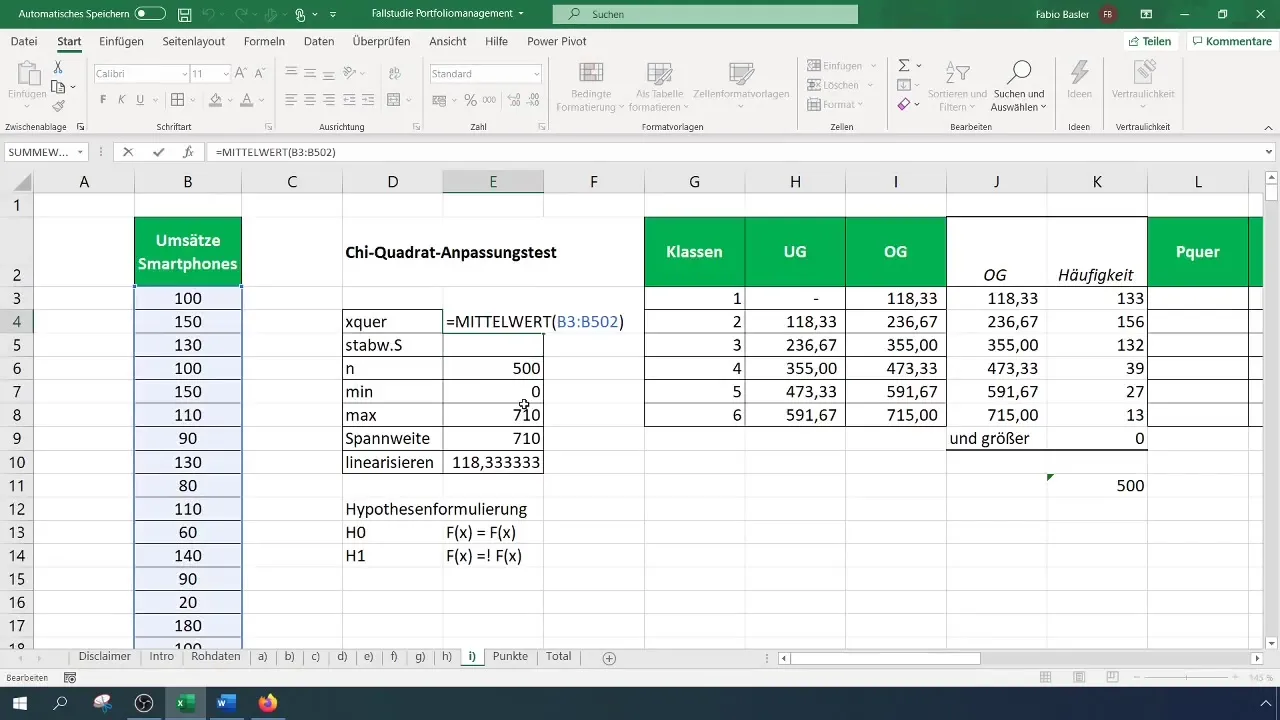
Langkah 5: Menghitung Frekuensi yang Diharapkan
Untuk menghitung frekuensi yang diharapkan, hitung probabilitas untuk setiap kelas berdasarkan distribusi normal yang diasumsikan. Anda memerlukan nilai tengah dan deviasi standar dari data Anda untuk ini.
Langkah 6: Menghitung Ukuran Uji
Hitung ukuran uji (Chi-Kuadrat) dengan rumus:
[ \chi^2 = \sum \frac{(O_i - E_i)^2}{E_i} ]
di mana (O_i) adalah frekuensi yang diamati dan (E_i) adalah frekuensi yang diharapkan. Anda dapat melakukan perhitungan ini di Excel dengan menyimpan komponen-komponen individu di sel-sel terpisah.
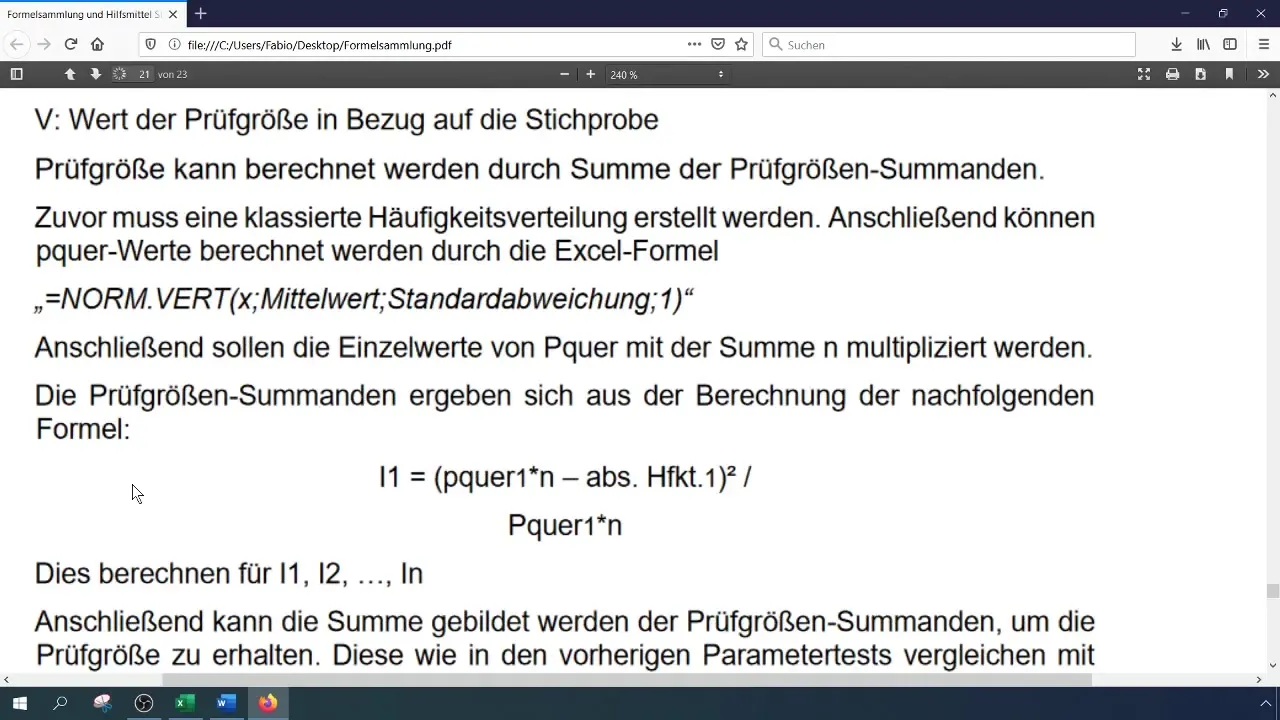
Langkah 7: Menghitung Nilai Kritis
Untuk mengevaluasi ukuran uji, Anda perlu menghitung nilai kritis ( \chi^2 ) untuk tingkat kepercayaan Anda dan jumlah derajat kebebasan. Jumlah derajat kebebasan untuk uji Chi-Kuadrat adalah (k - 1), di mana (k) adalah jumlah kelas.
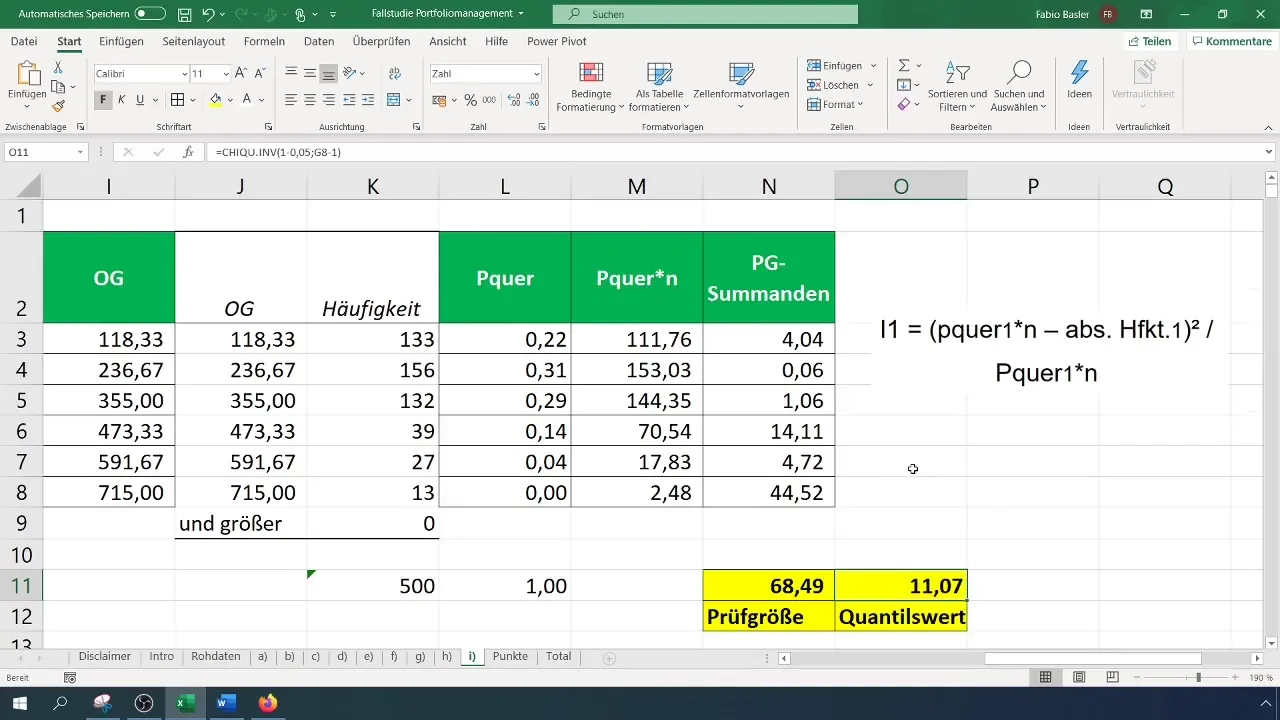
Langkah 8: Memeriksa Hipotesis
Bandingkan ukuran uji yang Anda hitung dengan nilai kritis. Jika ukuran uji lebih besar dari nilai kritis, tolak hipotesis nol, yang berarti data tidak berdistribusi normal. Jika tidak, terima hipotesis nol.
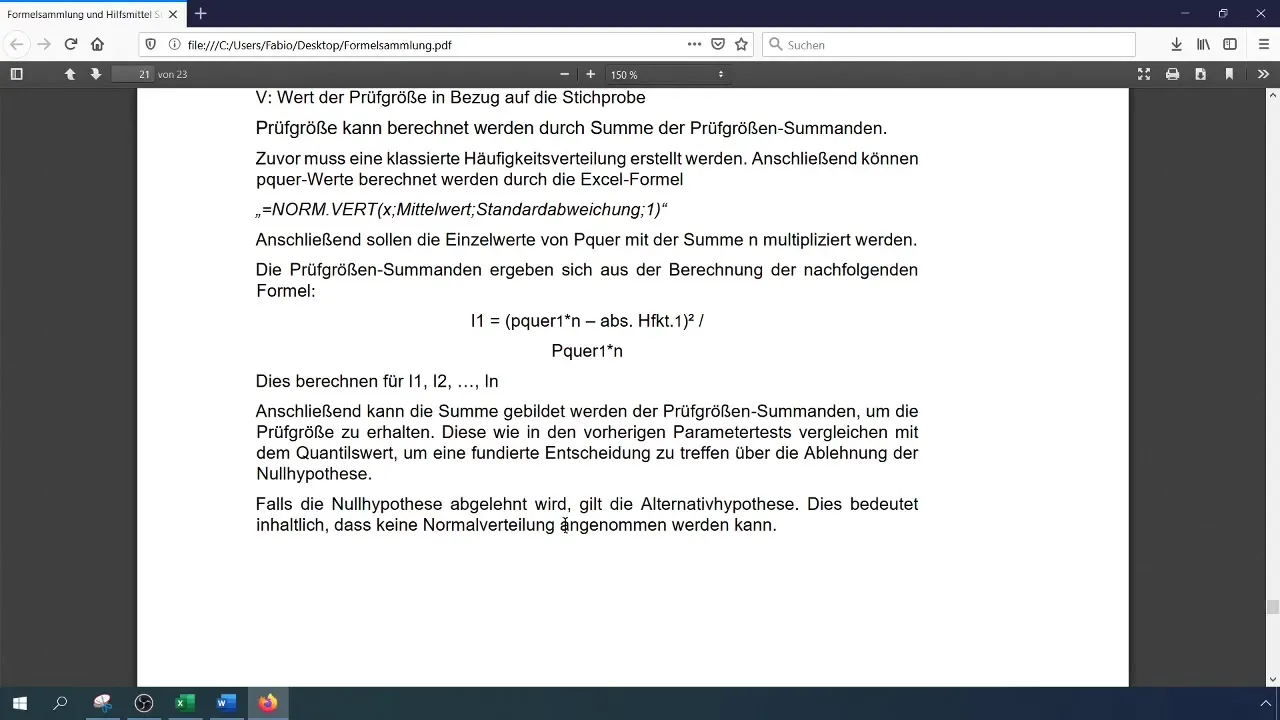
Langkah 9: Ringkasan Hasil
Catatlah hasil Anda dan perluas dengan data grafis dan uji hipotesis. Jangan lupa untuk memeriksa histogram Anda untuk memastikan visual bahwa distribusinya tidak normal.
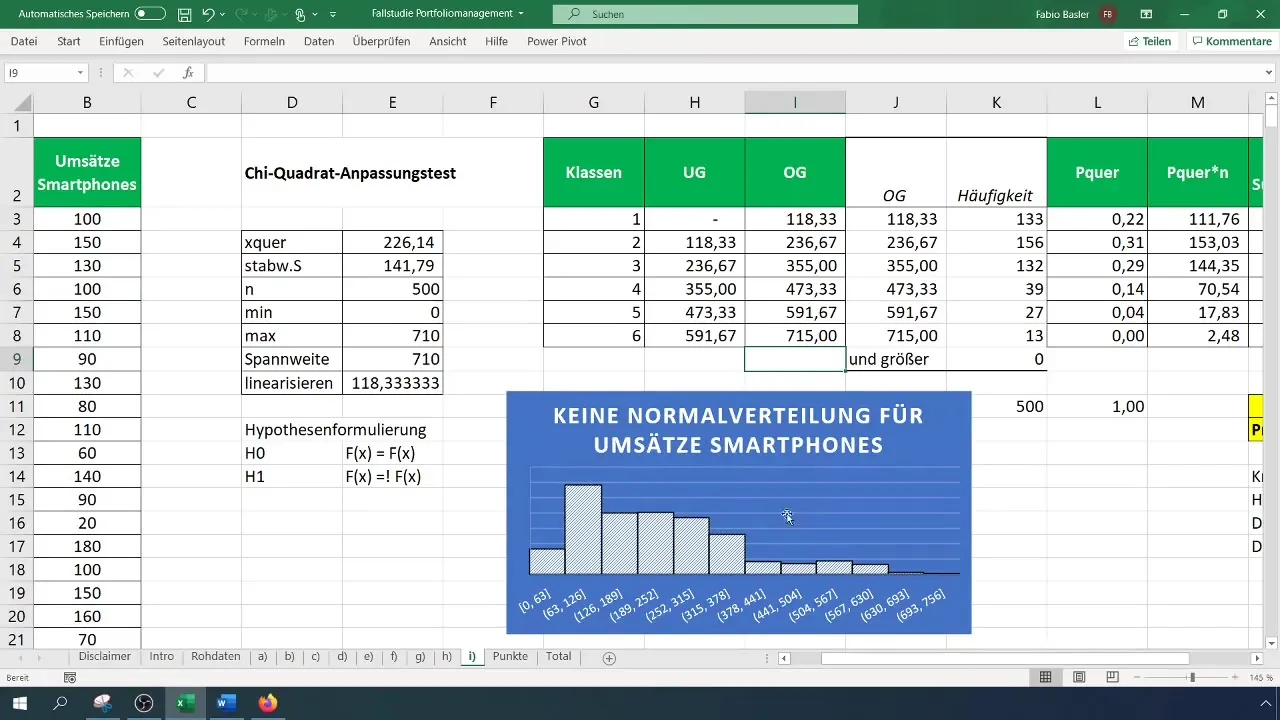
Ringkasan
Seiring dengan panduan ini, Anda belajar cara melakukan uji Chi-Kuadrat dalam Excel untuk menganalisis distribusi normal penjualan smartphone Anda. Langkah-langkah meliputi pembuatan tabel frekuensi bertingkat, perhitungan frekuensi yang diharapkan, ukuran uji, dan akhirnya perbandingannya dengan nilai kritis.
Pertanyaan Umum
Apa itu uji Chi-Kuadrat?Uji Chi-Kuadrat memeriksa apakah distribusi frekuensi yang diamati sesuai dengan distribusi normal.
Berapa banyak kelas yang dibutuhkan untuk tabel frekuensi?Paling tidak 5 hingga 10 kelas biasanya diperlukan agar data yang dianalisis bermakna.
Apa yang harus saya lakukan jika hipotesis nol ditolak?Jika Anda menolak hipotesis nol, ini berarti bahwa data tidak terdistribusi secara normal.
Bagaimana cara menghitung nilai kritis Chi-Kuadrat?Nilai kritis dibaca dari tabel distribusi Chi-Kuadrat berdasarkan derajat kebebasan dan tingkat signifikansi yang diinginkan.


