Test statistici sono un elemento centrale dell'analisi dei dati e della presa di decisioni. Specialmente nel campo della biotecnologia, può essere cruciale verificare le ipotesi sulla percentuale di successo dei principi attivi. In questo tutorial imparerai come eseguire in modo efficiente un Test a campione singolo (1-SP-Test) sul valore atteso con varianza nota in Excel.
Conclusioni principali
Questo tutorial ti fornirà:
- I fondamenti teorici del test a campione singolo.
- I passaggi per eseguire il test in Excel.
- L'interpretazione dei risultati.
Preparazione dei dati
Per eseguire il test a campione singolo in Excel, è necessario prima avere a disposizione i dati rilevanti. Nel nostro esempio, ipotizziamo di analizzare la percentuale di successo dei principi attivi. Si sa che la percentuale di successo media era del 59% in precedenza, con una deviazione standard di 19. Innanzitutto, è necessario inserire i dati in una tabella Excel.
Assicurati che i tuoi dati siano organizzati in colonne in modo da potervi accedere in seguito. Una buona organizzazione ti aiuterà a seguire più agevolmente i singoli passaggi.
Panoramica del test
Il test a campione singolo serve a verificare se il valore medio del successo differisce significativamente da un valore prestabilito. In questo caso, verifichiamo se la percentuale di successo del 59% può essere nettamente aumentata in futuro.
Formulazione delle ipotesi
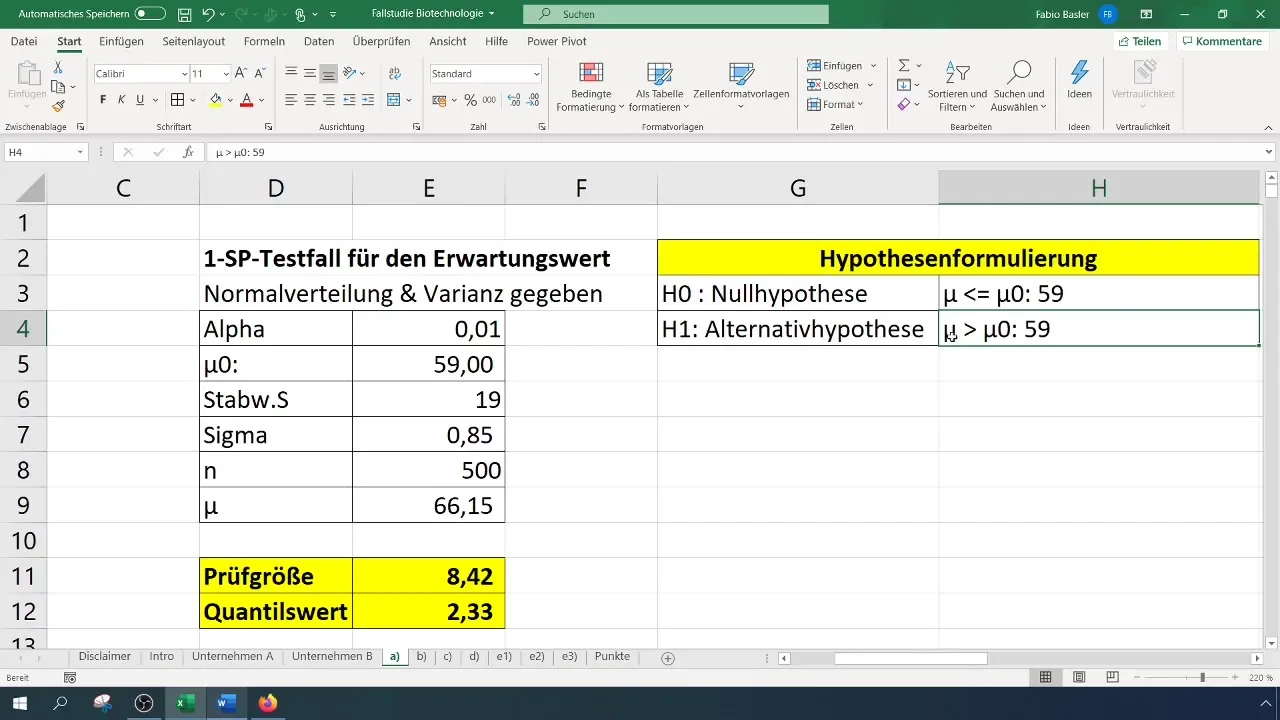
Le ipotesi formulate per il test sono cruciali:
- Ipotesi nulla (H0): Il vero valore atteso è uguale a 59 (σ = 59%).
- Ipotesi alternativa (H1): Il vero valore atteso è maggiore del 59%.
Nella formulazione delle ipotesi, è importante concentrarsi su ciò che deve essere testato esattamente e su come si presenta nel tuo contesto.
È importante distinguere chiaramente tra l'ipotesi nulla e l'ipotesi alternativa, poiché esse costituiscono la base per i calcoli successivi.
Raccolta del campione
Per il nostro test, prendiamo un campione di 500 principi attivi. È importante notare che la selezione del campione deve essere rappresentativa e garantire tramite il metodo appropriato che i risultati possano essere realisticamente estesi alla popolazione complessiva.
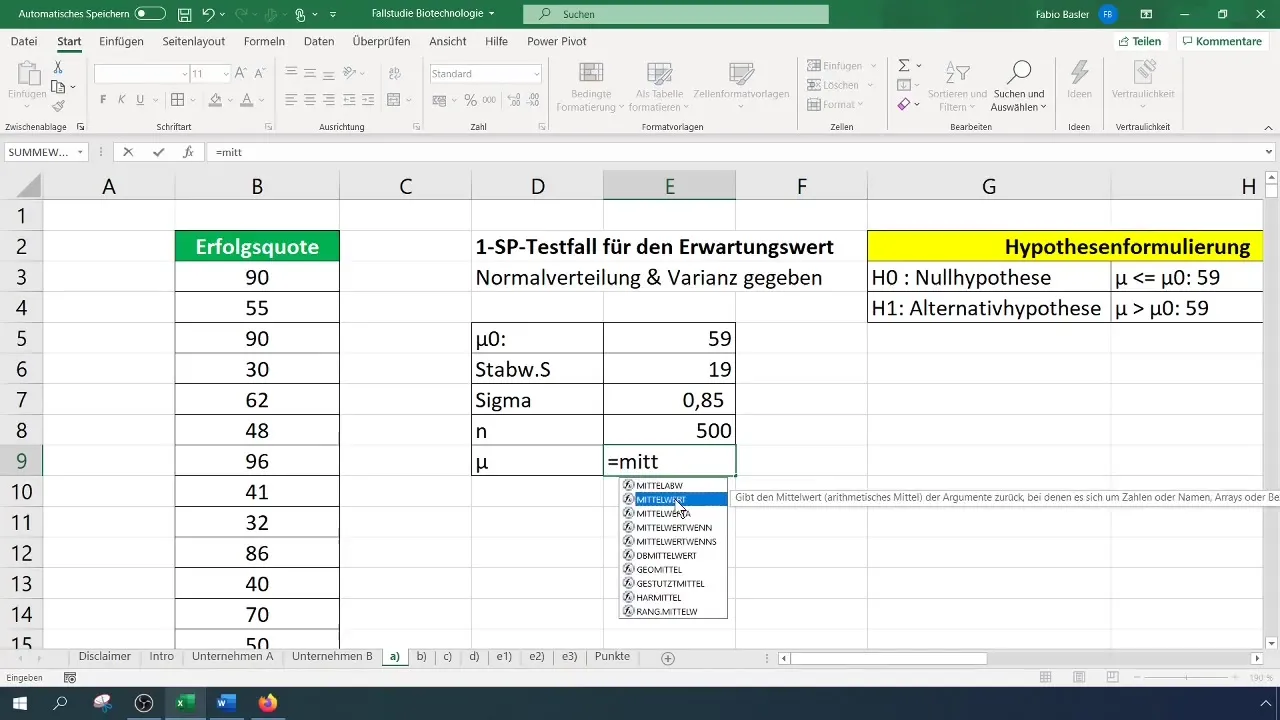
Per il test, calcola innanzitutto la media aritmetica. Questo dovrebbe essere facilmente realizzabile utilizzando la formula corrispondente in Excel.
Calcolo della statistica di test
La statistica di test per un test a campione singolo è determinata dalla seguente formula:
[ Z = \frac{\bar{x} - \mu_0}{\sigma/\sqrt{n}} ]
Dove (\bar{x}) è la media del tuo campione, (\mu_0) è il valore atteso (in questo caso 59), (\sigma) è la deviazione standard (qui 19) e (n) è il numero di campioni (500).
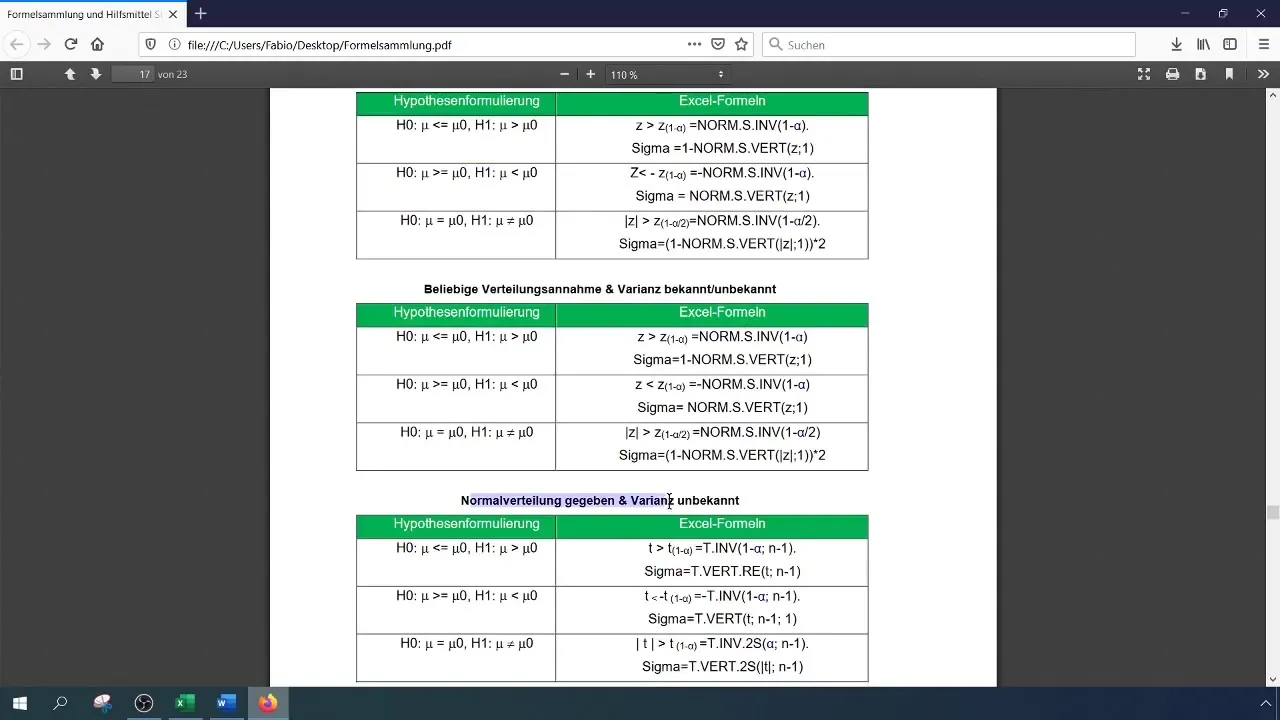
Dopo aver inserito i valori nella formula, calcola la statistica di test per determinare se è significativa o no.
Calcolo del valore critico
Per un livello di significatività del 1% (0,01), è necessario leggere o calcolare il valore critico. Puoi farlo in Excel utilizzando la funzione NORM.S.INV.
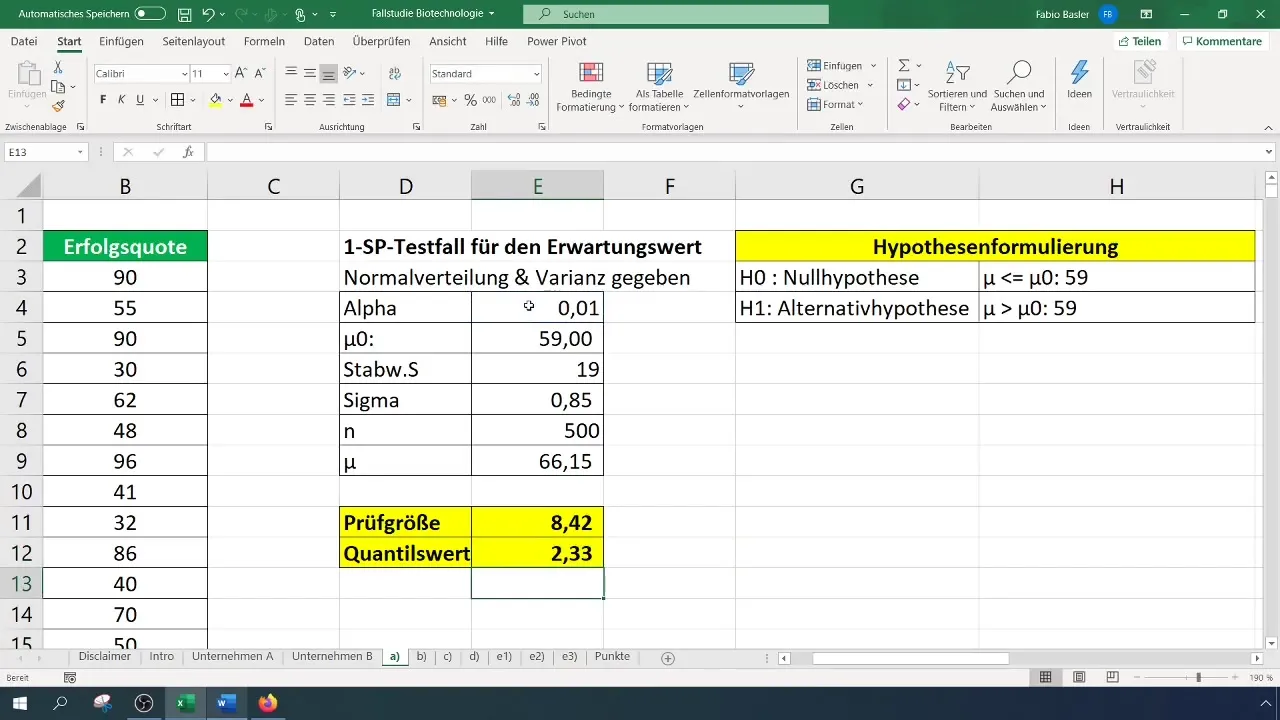
La formula è la seguente:
[ \text{NORM.S.INV}(1 - \alpha) ]
Dove (\alpha) è il livello di significatività (0,01). Il valore ottenuto sarà la base per il confronto con la statistica di test.
Esecuzione del test
Dopo aver ottenuto sia la statistica di test che il valore critico, confrontali:
- Se la statistica di test è maggiore del valore critico, si rigetta l'ipotesi nulla.
- Altrimenti, non si può rifiutare l'ipotesi nulla.
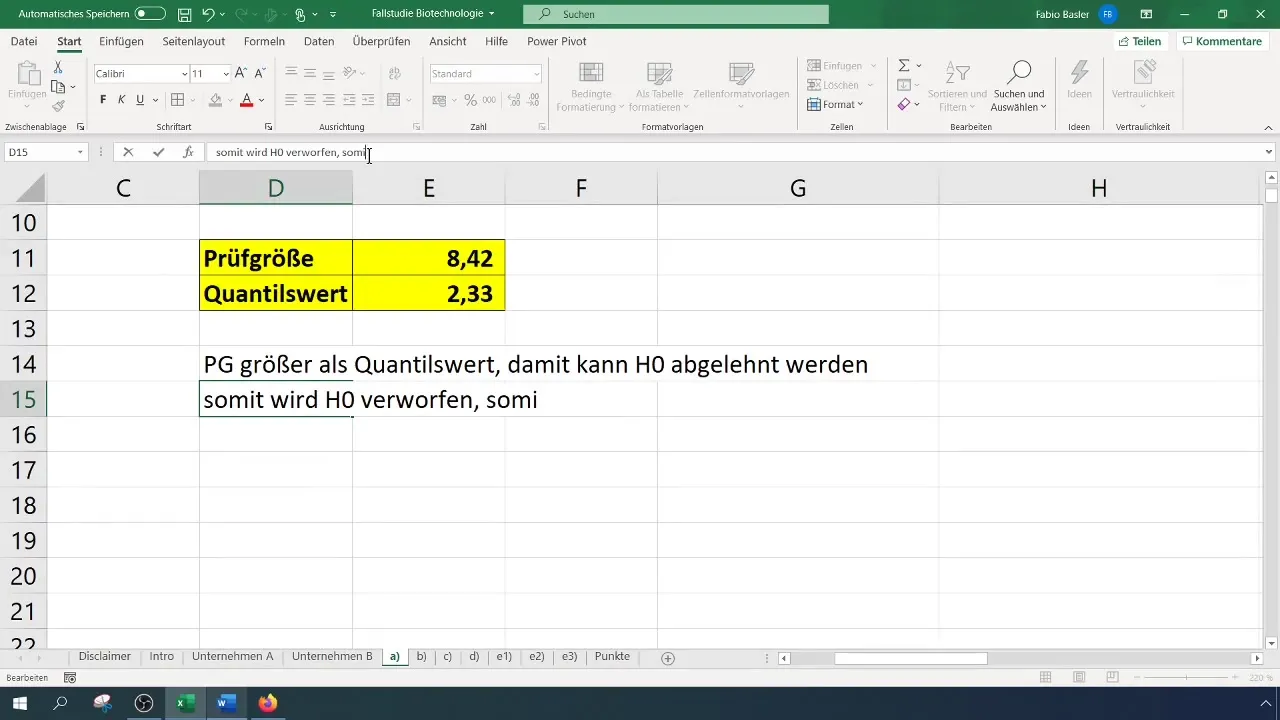
Nel nostro caso, otteniamo una statistica di test di 8,4, che supera il valore critico di 2,33. Pertanto possiamo respingere l'ipotesi nulla. Questo suggerisce che il tasso di successo è stato significativamente migliorato.
Interpretazione dei risultati
Dopo aver eseguito il test e ottenuto i risultati, dovresti interpretarli in un contesto chiaro. Il rifiuto dell'ipotesi nulla significa che il nuovo valore testato è significativamente diverso dal passato, nel caso specifico del 59%.
Queste informazioni sono di grande importanza per il processo decisionale strategico nella tua azienda. Confermano che gli sforzi per migliorare il tasso di successo sono stati efficaci.
Riepilogo
In questo tutorial hai imparato come eseguire un test 1-SP per il valore atteso in Excel. Attraverso uno studio di caso, hai potuto seguire i passaggi dall'formulazione delle ipotesi al calcolo dei dati e all'interpretazione dei risultati. Queste conoscenze sono preziose non solo per le valutazioni scientifiche, ma anche per le applicazioni pratiche in azienda.
Domande frequenti
Cos'è il test 1-SP?Il test 1-SP è un test statistico per verificare se la media di un campione è significativamente diversa da un valore prefissato.
Come formulare ipotesi per il test?Le ipotesi sono composte da un'ipotesi nulla (H0) e da un'ipotesi alternativa (H1) che documentano lo stato da verificare.
Come calcolare la statistica di test?La statistica di test è determinata dalla formula ( Z = \frac{\bar{x} - \mu_0}{\sigma/\sqrt{n}} ).
Cosa succede se la statistica di test è maggiore del valore critico?Se la statistica è maggiore del valore critico, si respinge l'ipotesi nulla.
Quale ruolo ha il livello di significatività?Il livello di significatività indica con quale probabilità sei disposto a accettare un errore nel rifiutare erroneamente l'ipotesi nulla.


