Il test t a due campioni è uno strumento essenziale in statistica quando si desidera esaminare la differenza tra due medie. In questo tutorial imparerai come eseguire questo test in modo semplice ed efficace in Excel. Attraverso un esempio nel campo della biotecnologia, imparerai a confrontare e analizzare statisticamente i tassi di successo di due aziende concorrenti.
Principali conclusioni
- Applicazione del test t a due campioni per analizzare la differenza tra due medie.
- Formulazione e verifica delle ipotesi.
- Utilizzo di Excel per calcolare e visualizzare i risultati.
Guida passo dopo passo
Per prima cosa, inizieremo creando i dati necessari e eseguendo il test in Excel.
Passo 1: Preparare i dati
Inizia raccogliendo i dati grezzi sui tassi di successo delle due aziende. Supponiamo che tu abbia i dati delle aziende A e B, con un campione di 100 record per azienda.

Passo 2: Calcolare la dimensione del campione e le medie
Crea una tabella in Excel per confrontare i campioni e le loro medie. Calcola prima la dimensione del campione (N) per entrambe le aziende e la media (X).

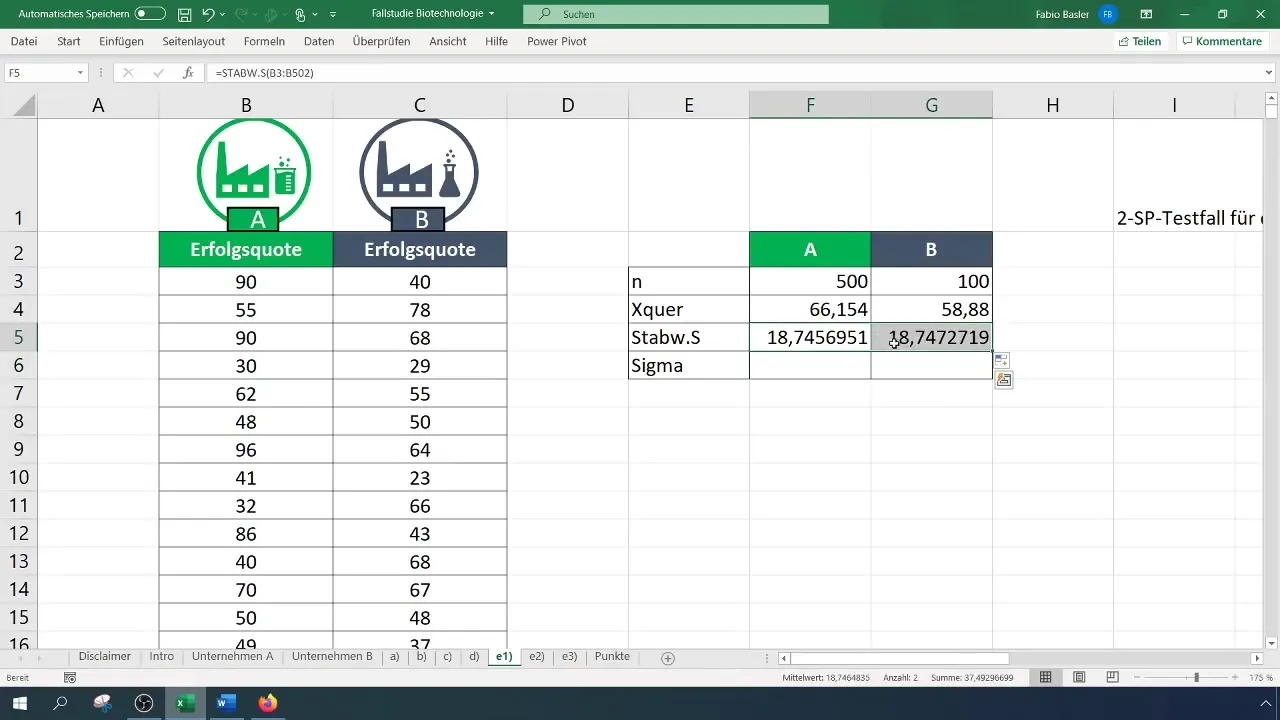
Passo 3: Calcolare le deviazioni standard
Calcola la deviazione standard per entrambe le aziende. Questi valori sono importanti per effettuare la variazione e i calcoli successivi.
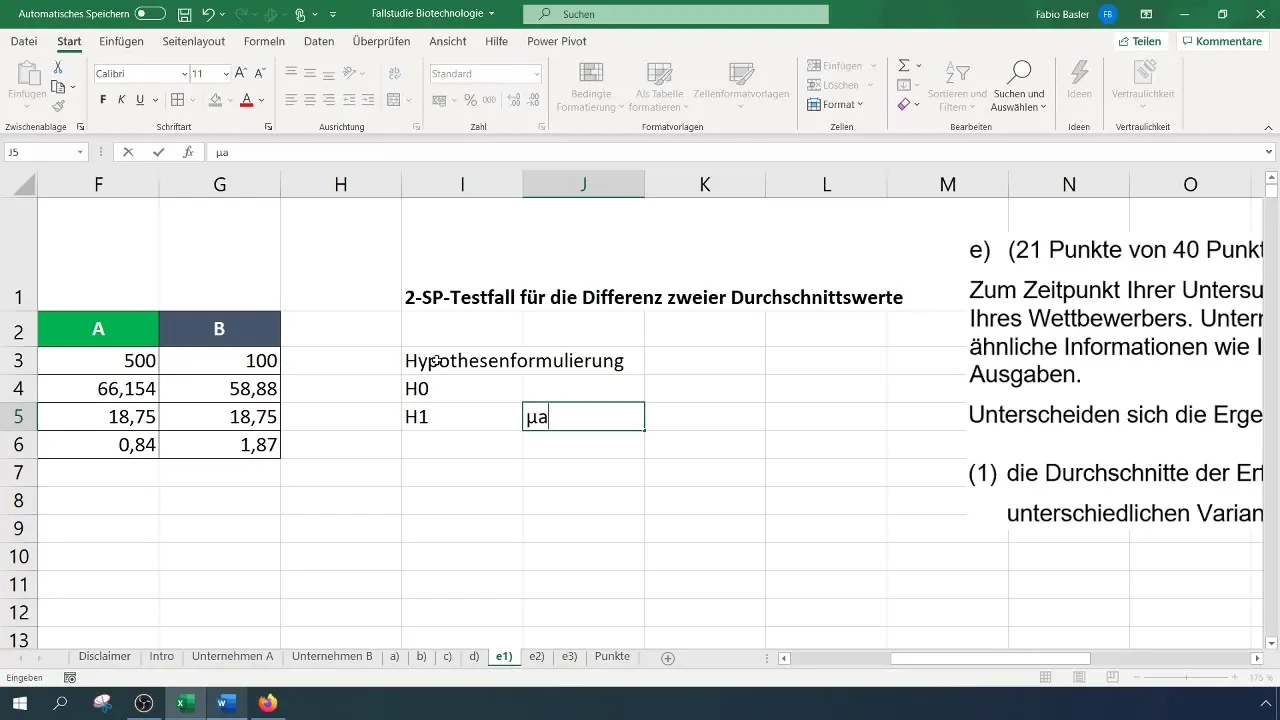
Passo 4: Formulare ipotesi
Formulare l'ipotesi nulla (H_0): I valori medi dei tassi di successo delle aziende A e B sono uguali. L'ipotesi alternativa (H_1): I valori medi dei tassi di successo sono diversi.
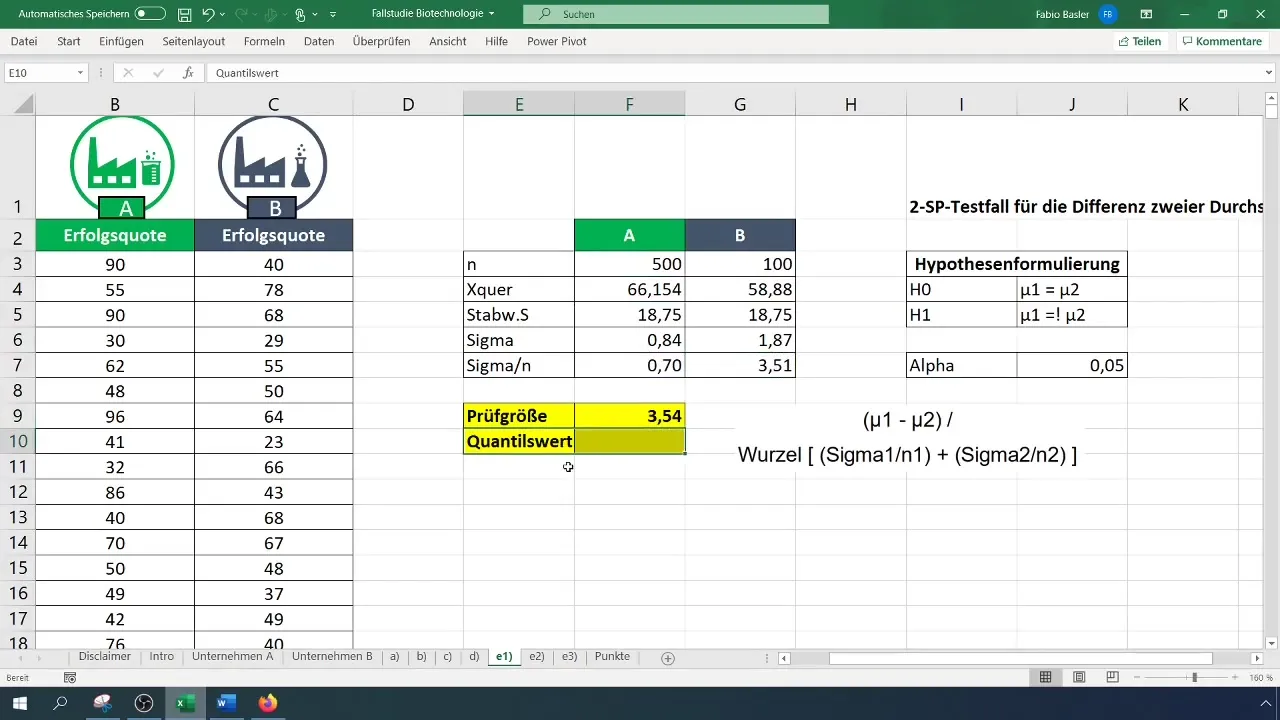
Passo 5: Calcolare la statistica del test
Per calcolare la statistica del test, utilizza la formula per il test t. Calcola la differenza tra le medie e dividi per la radice della somma delle varianze per ciascun campione.
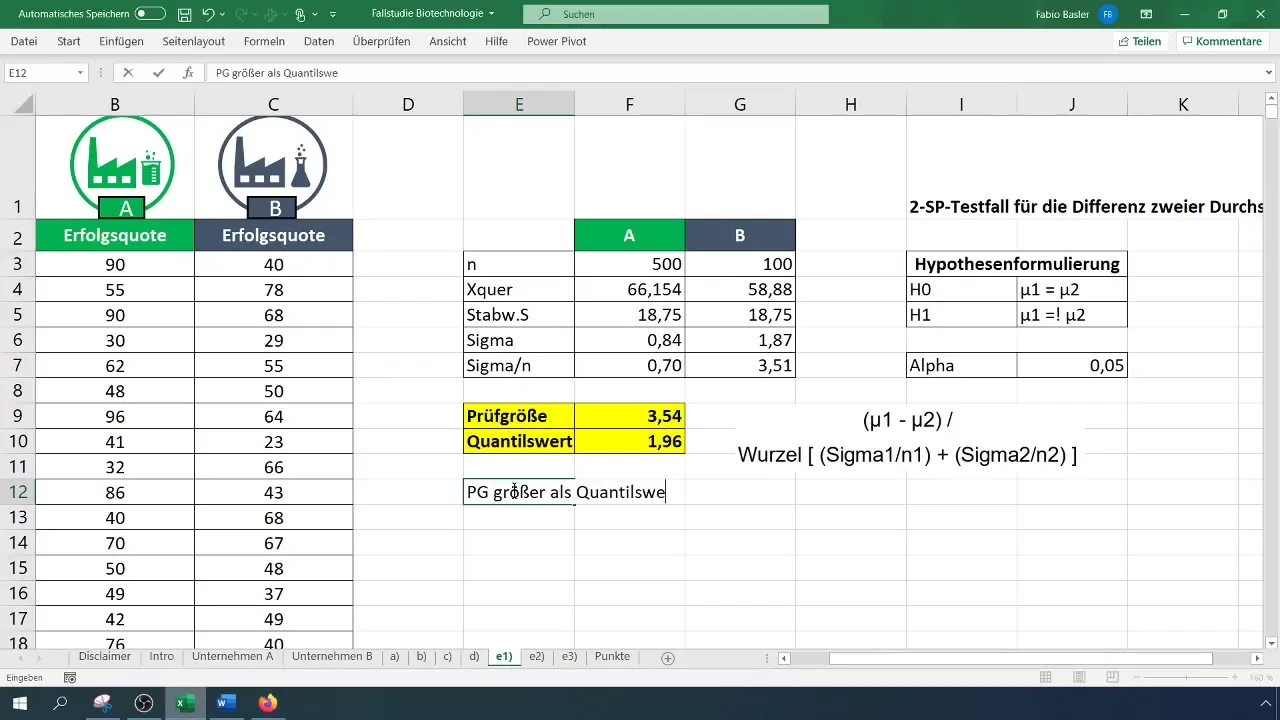
Passo 6: Calcolare il valore critico
Utilizza la distribuzione t bidirezionale per trovare il valore critico. Imposta il livello alfa a 0,05. Verifica la tabella della distribuzione t o calcola direttamente il fattore in Excel.
Passo 7: Decisione sull'ipotesi
Confronta la statistica del test calcolata con il valore critico. Se la statistica del test è maggiore del valore critico, rifiuta l'ipotesi nulla (H_0) e conferma l'ipotesi alternativa (H_1).
Passo 8: Interpretare i risultati
Infine, interpreta i risultati. In questo esempio, le medie dei tassi di successo delle due aziende sono state ritenute significativamente diverse.
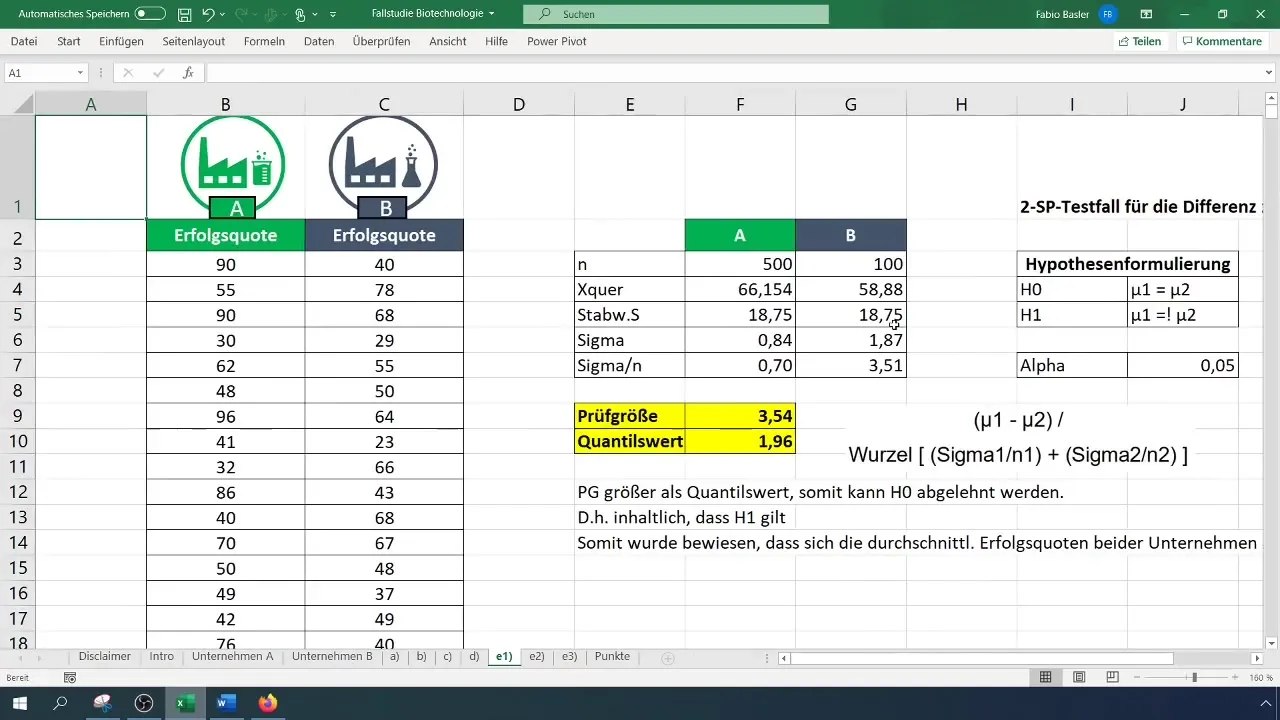
Riassunto
Hai imparato come eseguire un test t a due campioni in Excel per esaminare le differenze nelle medie di due gruppi. I passaggi dalla preparazione dei dati alla formulazione delle ipotesi all'interpretazione dei risultati sono cruciali per prendere decisioni valide e informate.
Domande frequenti
Cosa significa un test t a due campioni?Il test t a due campioni confronta le medie di due gruppi per determinare se sono significativamente diverse.
Come si formulano le ipotesi?L'ipotesi nulla (H_0) afferma che le medie sono uguali, mentre l'ipotesi alternativa (H_1) afferma che sono diverse.
Come si calcola la statistica del test?La statistica del test viene calcolata dividendo la differenza tra le medie per la radice della somma delle varianze.
Cosa fare dopo il calcolo?Confronta la statistica del test con il valore critico per decidere se puoi rifiutare l'ipotesi nulla.
Perché è importante la deviazione standard?La deviazione standard aiuta a capire la variabilità dei dati, che è fondamentale per il calcolo della statistica del test.


