Il test di adattamento del chi-quadrato rappresenta un metodo semplice per verificare l'ipotesi che una serie di dati data segua una distribuzione normale. In questa guida imparerai come eseguire il test del chi-quadrato su Excel per determinare se i ricavi degli smartphone seguano una distribuzione normale. Affronteremo il processo passo dopo passo, che va dalla creazione di una tabella di frequenza classificata al calcolo della statistica del test e al confronto con il valore critico del chi-quadrato.
Principali conclusioni
- Il test di adattamento del chi-quadrato aiuta nella verifica delle distribuzioni normali.
- È importante creare una tabella di frequenza classificata.
- La statistica del test viene confrontata con un valore critico per rifiutare o accettare l'ipotesi nulla.
Istruzioni passo dopo passo
Passo 1: Preparare i dati
Per eseguire il test del chi-quadrato, devi prima ottenere i dati. Copia i ricavi degli smartphone in un foglio di lavoro di Excel. Assicurati che i tuoi dati siano organizzati in una singola colonna.

Passo 2: Creare un istogramma
Per ottenere i primi indizi visivi sulla distribuzione, crea un istogramma dei tuoi dati. Vai su "Inserisci" e seleziona "Grafici". Aggiungi un istogramma selezionando l'intervallo dei dati.
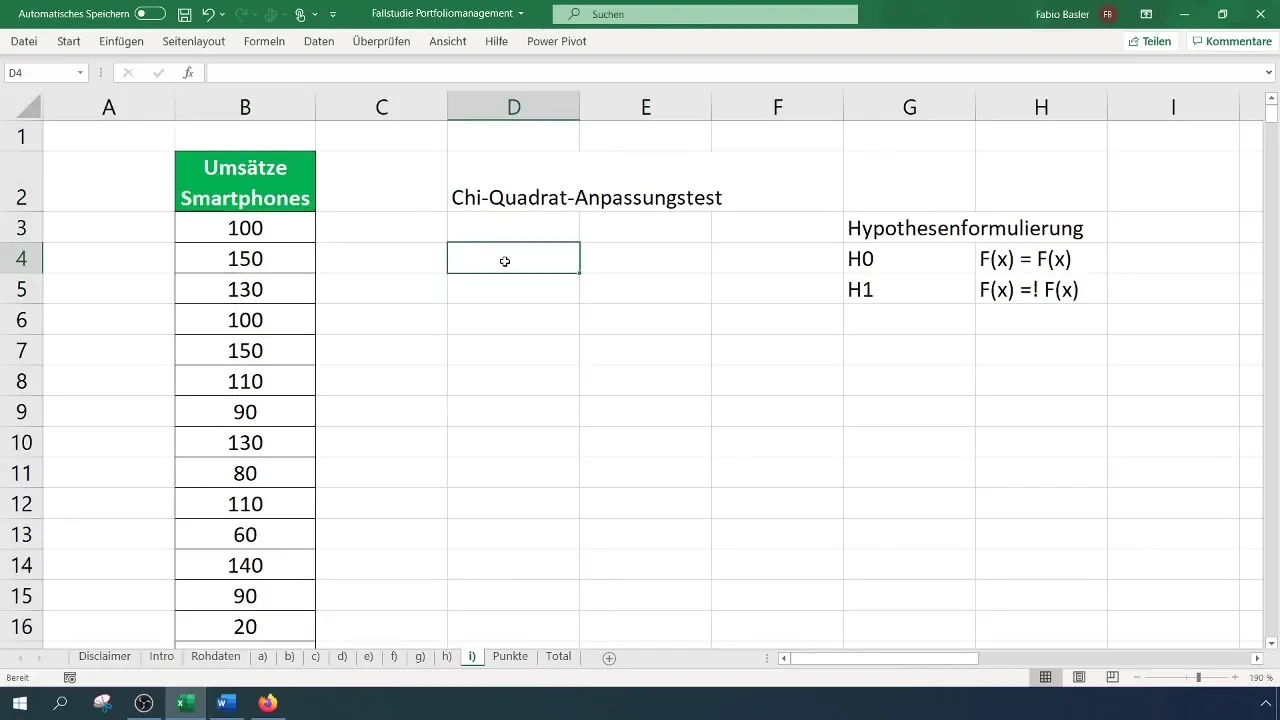
Passo 3: Creare una tabella di frequenza classificata
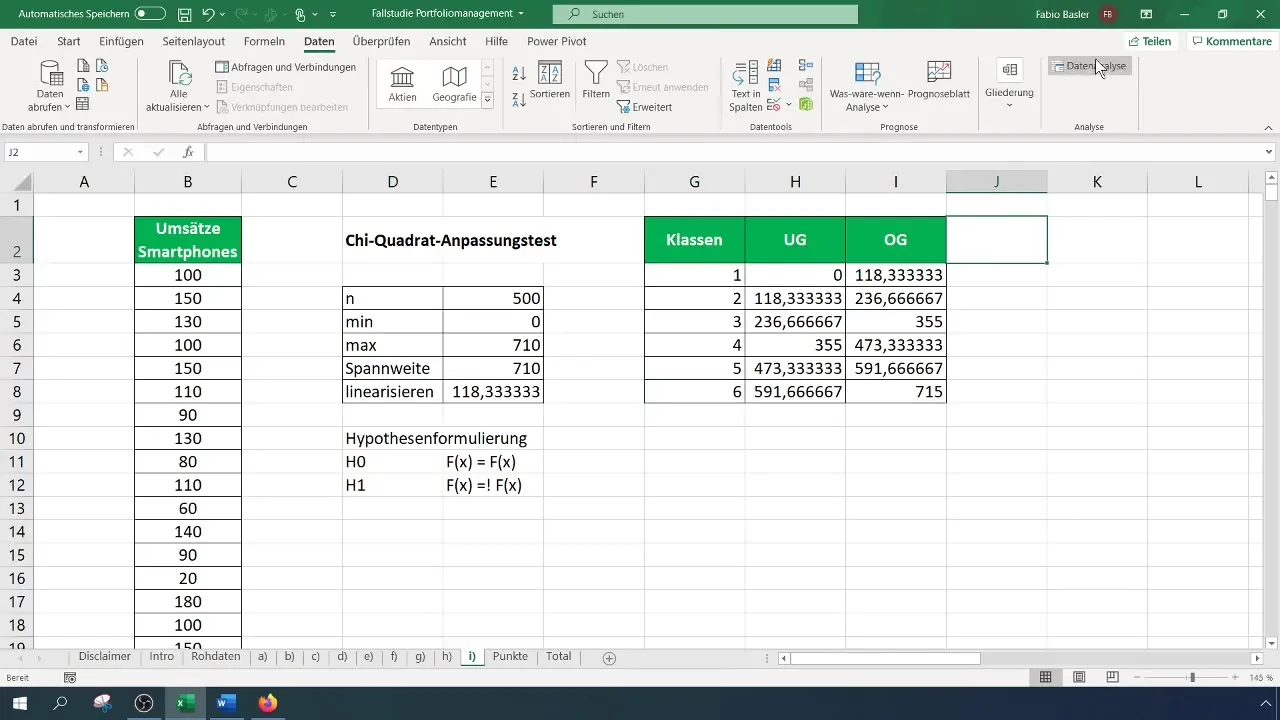
Per il test di chi-quadrato, è necessaria una tabella di frequenza classificata. Determina innanzitutto il numero di classi per la tua tabella - in questo caso useremo sei classi. Calcola la larghezza degli intervalli e crea la tabella di conseguenza.
Passo 4: Calcolare le frequenze
Devi ora calcolare le frequenze osservate per ogni classe. Vai su "Analisi dati" nel menu e seleziona "Istogramma". Scegli l'intervallo di input per i tuoi dati e i limiti di classe. Determina l'intervallo di output per la tabella di frequenza.
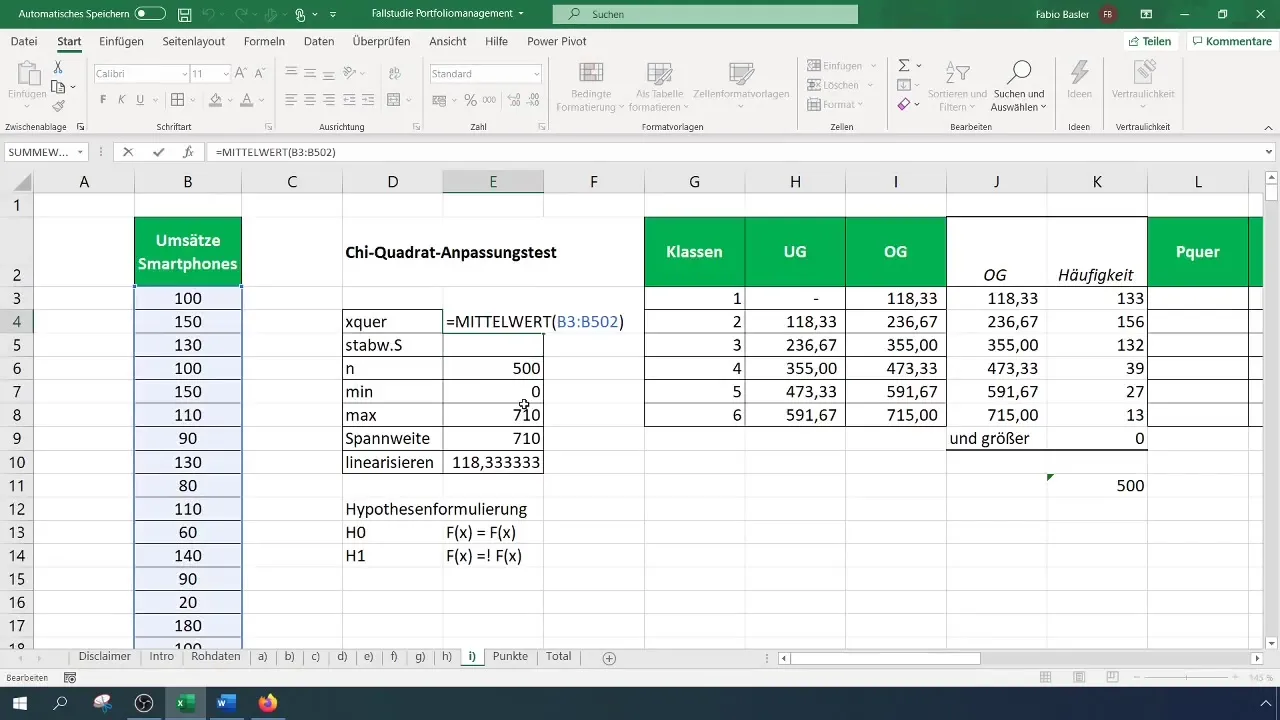
Passo 5: Calcolare le frequenze attese
Per determinare le frequenze attese, calcola le probabilità per ogni classe basate sulla distribuzione normale ipotizzata. Per questo hai bisogno della media e della deviazione standard dei tuoi dati.
Passo 6: Calcolare la statistica del test
Calcola la statistica del test (chi-quadrato) con la formula:
[ \chi^2 = \sum \frac{(O_i - E_i)^2}{E_i} ]
dove (O_i) sono le frequenze osservate e (E_i) sono le frequenze attese. Puoi eseguire questo calcolo in Excel memorizzando i singoli componenti in celle separate.
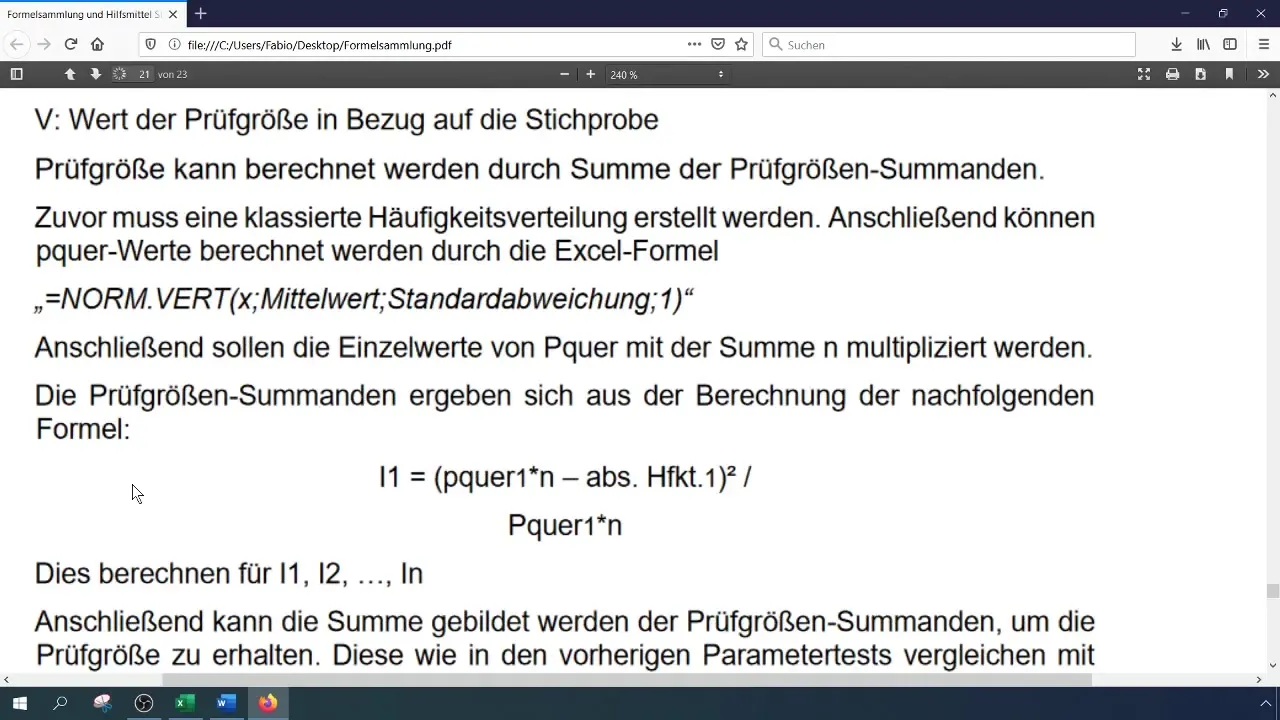
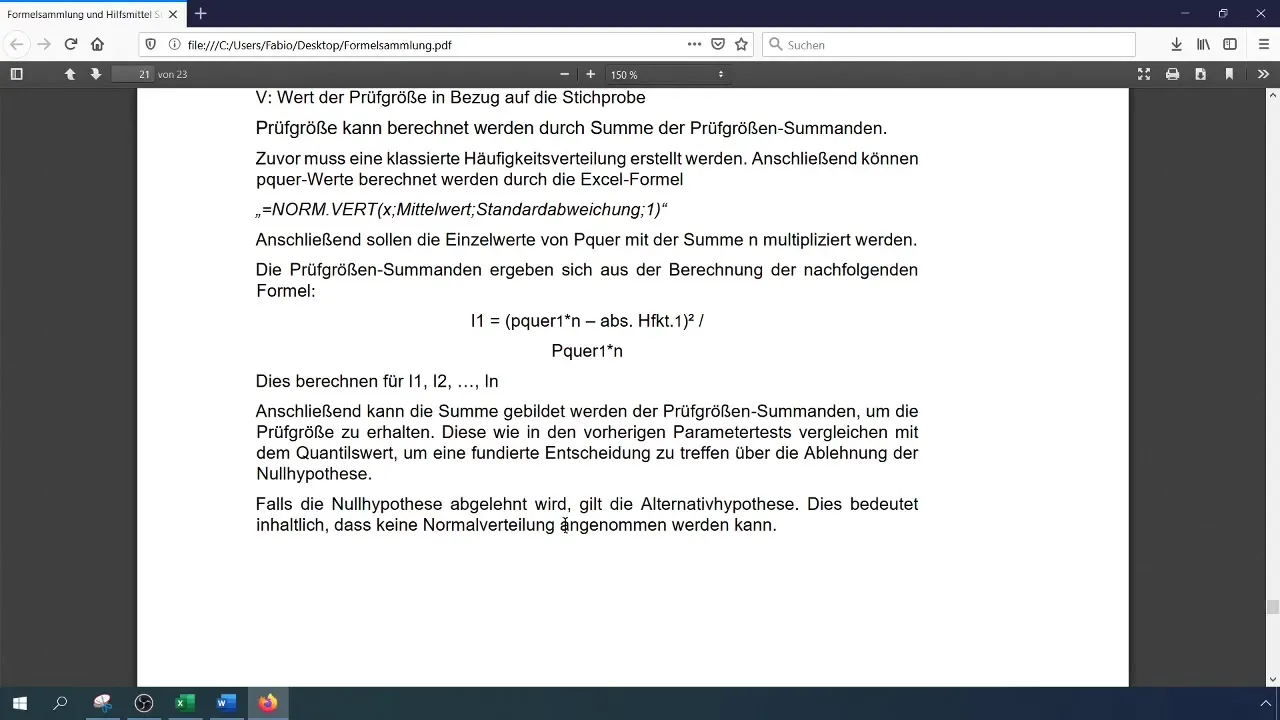
Passo 7: Calcolare il valore critico
Per valutare la statistica del test, devi calcolare il valore critico ( \chi^2 ) per il livello di significatività e il numero di gradi di libertà. Il numero di gradi di libertà per il test del chi-quadrato è (k - 1), dove (k) è il numero di classi.
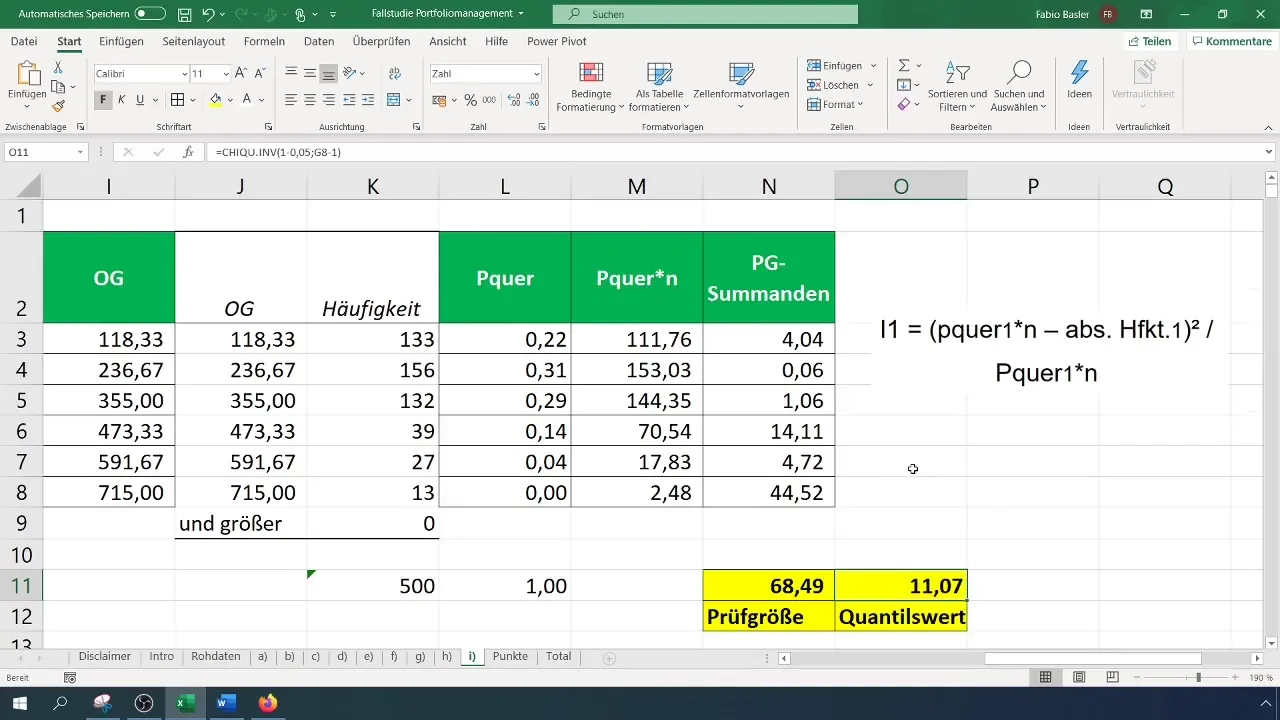
Passo 8: Verificare le ipotesi
Confronta la statistica del test calcolata con il valore critico. Se la statistica del test è maggiore del valore critico, rifiuta l'ipotesi nulla, il che significa che i dati non sono distribuiti normalmente. Altrimenti accetti l'ipotesi nulla.
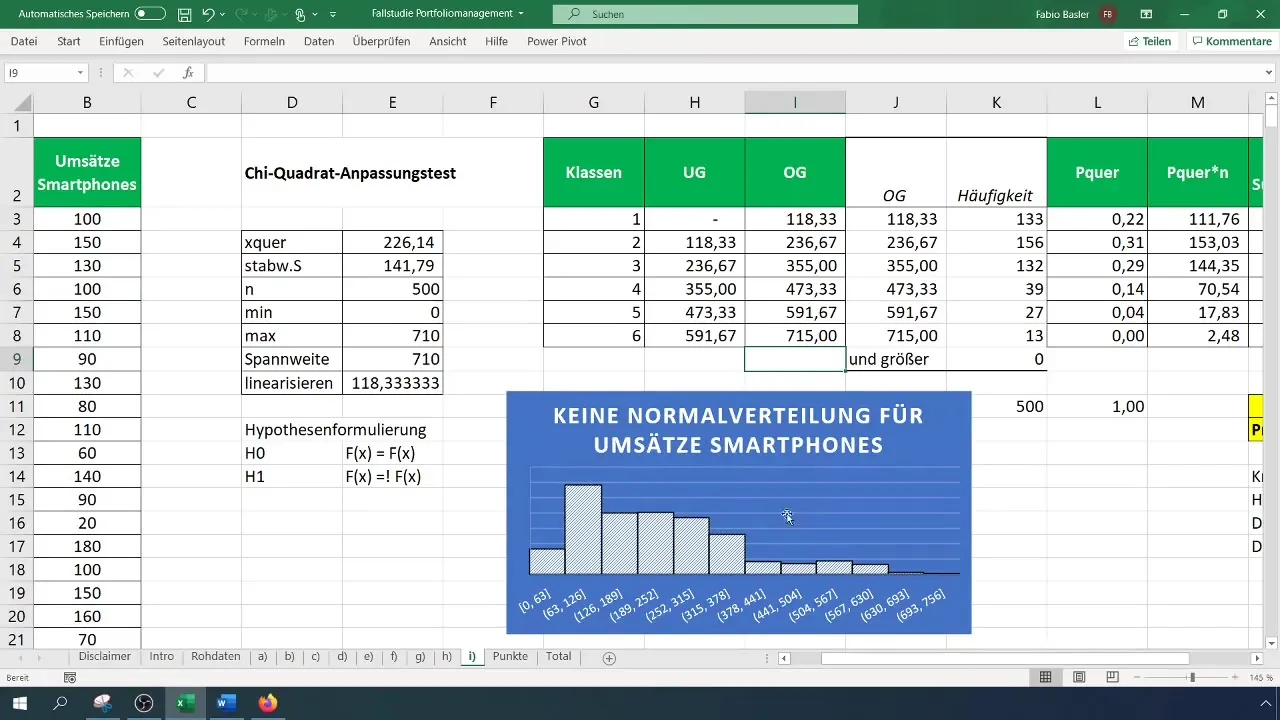
Passo 9: Riassumere i risultati
Mantieni traccia dei tuoi risultati e arricchiscili con i dati grafici e i test ipotetici. Non dimenticare di controllare il tuo istogramma per confermare visivamente che la distribuzione non è normale.
Riepilogo
Nel corso di questa guida hai imparato come eseguire il test di adattamento Chi-quadro in Excel per analizzare la distribuzione normale dei tuoi ricavi degli smartphone. I passaggi includono la creazione di una tabella di frequenza classificata, i calcoli per le frequenze attese, la statistica di prova e infine il confronto di queste con il valore critico.
Domande frequenti
Cos'è il test di adattamento Chi-quadro?Il test di adattamento Chi-quadro verifica se la distribuzione delle frequenze osservate corrisponde a una distribuzione normale.
Quante classi sono necessarie per la tabella di frequenza?Nel caso generale, sono consigliate almeno 5-10 classi per analizzare i dati in modo significativo.
Cosa fare se l'ipotesi nulla viene rifiutata?Se rifiuti l'ipotesi nulla, significa che i dati non sono distribuiti in modo normale.
Come calcolare il valore critico Chi-quadro?Il valore critico viene letto da una tabella di distribuzione Chi-quadro in base ai gradi di libertà e al livello di significatività desiderato.


