Efficiente analisi dei dati pivot multidimensionale in Excel

L'analisi dei dati del sondaggio è una delle attività più importanti nell'ambito dell'analisi dei dati. In particolare, utilizzando le tabelle pivot in Excel, puoi rendere questa analisi più chiara. In questa guida ti mostriamo come creare tabelle pivot multidimensionali e quali calcoli puoi eseguire per estrarre indicatori preziosi dai tuoi dati del sondaggio.

Principali conclusioni

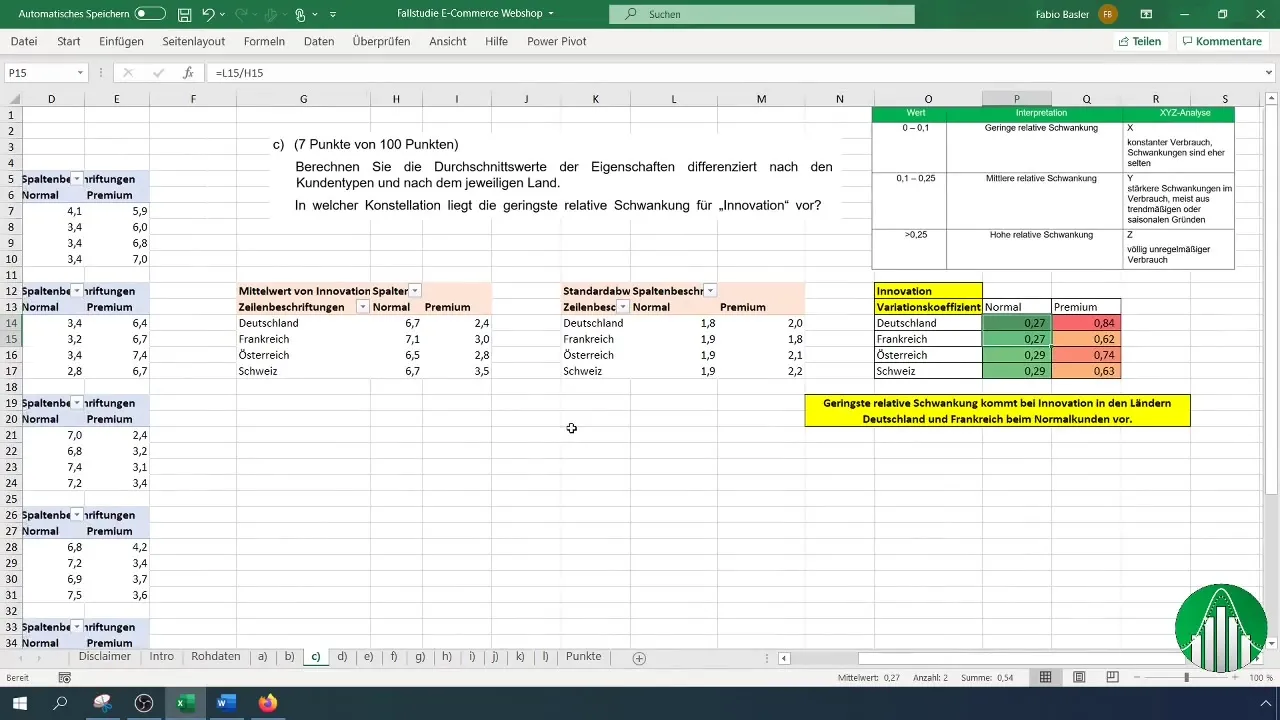
• Calcolo della media delle risposte al sondaggio per tipo di cliente e paese.
• Calcolo della variazione relativa delle risposte, in particolare per quanto riguarda le valutazioni delle innovazioni.
• Utilizzo efficiente delle tabelle pivot per la rappresentazione e l'analisi dei dati del sondaggio.

Istruzioni passo dopo passo

Passo 1: Creare una tabella pivot

Per prima cosa, devi creare la tabella pivot in Excel. Vai alla barra dei menu e seleziona "Inserisci". Quindi clicca sull'opzione per le tabelle pivot. Si aprirà una finestra di dialogo dove potrai selezionare la fonte dati. In questo caso, seleziona l'intervallo rilevante dei tuoi dati del sondaggio.

Inserisci la tabella pivot in un foglio di lavoro esistente e seleziona l'intervallo specifico in cui desideri memorizzare i tuoi dati.

Passo 2: Calcolare i valori medi

Successivamente, iniziamo a calcolare i valori medi. Trascina il primo indicatore, ad esempio "Consegna", nel campo dei valori della tabella pivot. Assicurati di cambiare il calcolo da "Somma" a "Media".

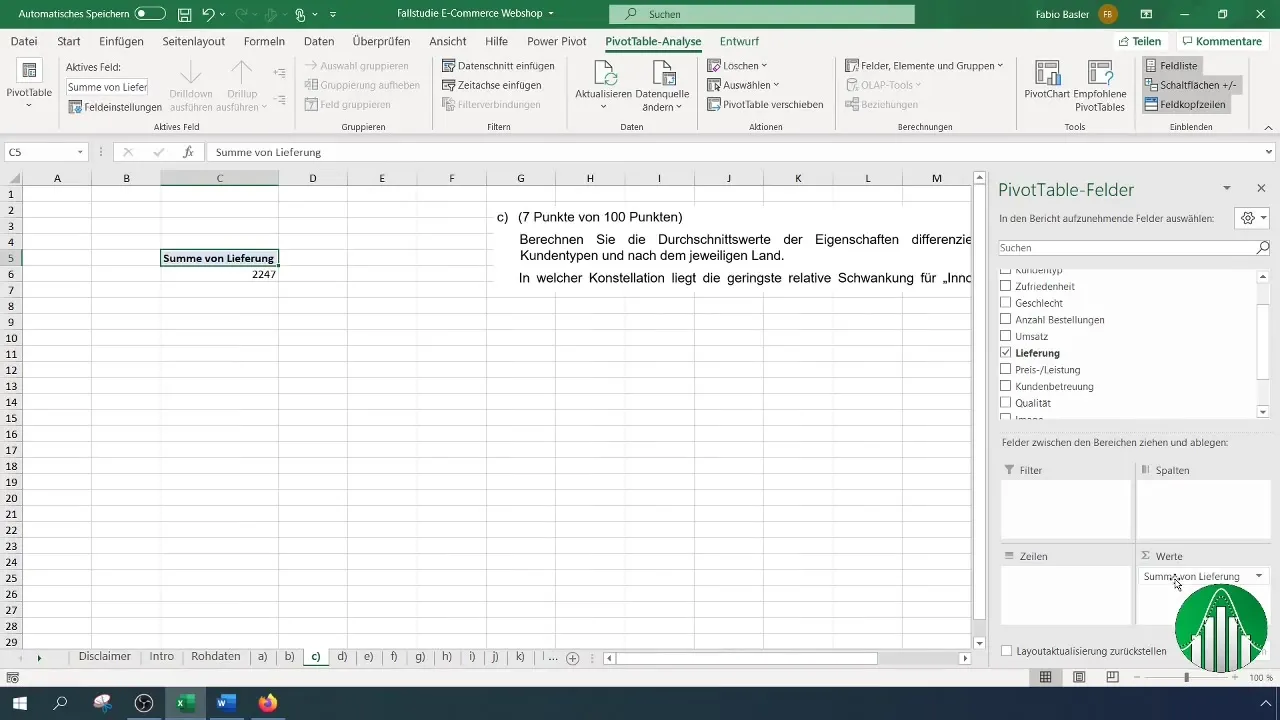
Ora hai calcolato i valori medi per la Consegna per tipi di cliente e paesi. Ripeti questo procedimento per tutti e sei i tratti del tuo sondaggio.

Passo 3: Aggiungere altri indicatori

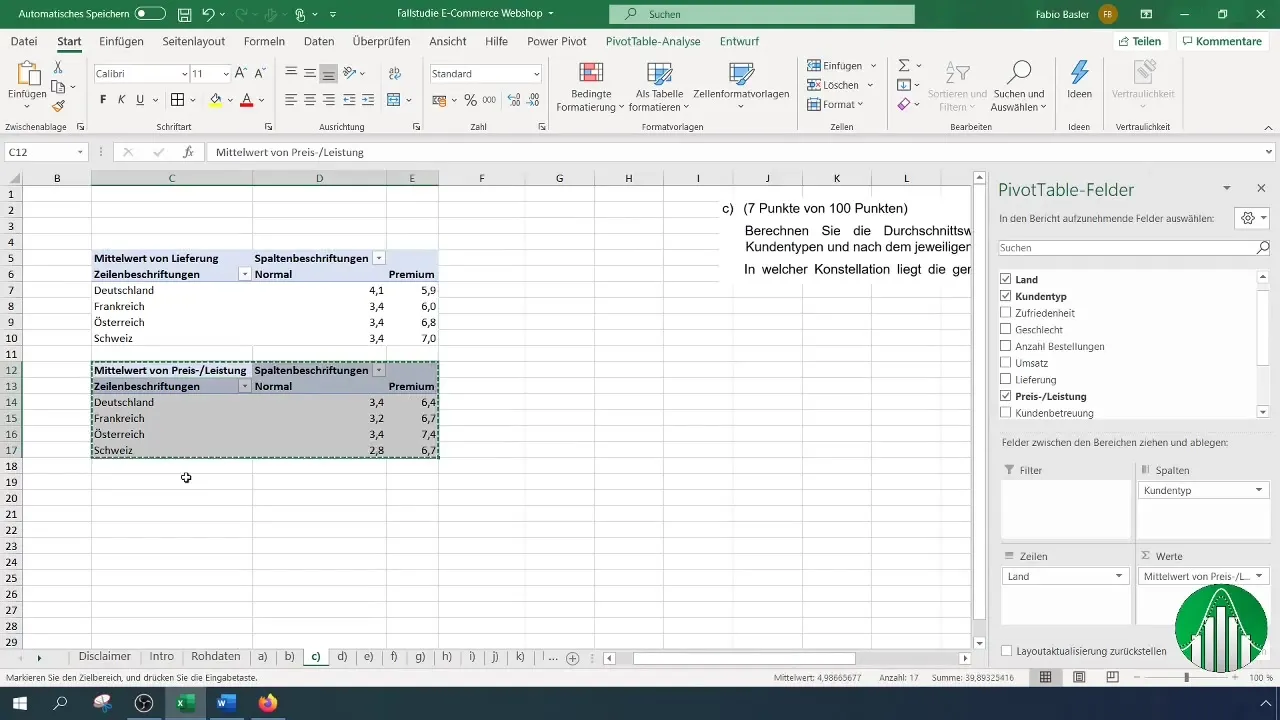
Per calcolare ulteriori indicatori, copia la tabella pivot già creata e incollala sotto. Cambia quindi di volta in volta gli indicatori da "Consegna" a "Rapporto qualità-prezzo", "Assistenza clienti" e così via. Ad ogni cambio, assicurati di tornare da Somma a Media.

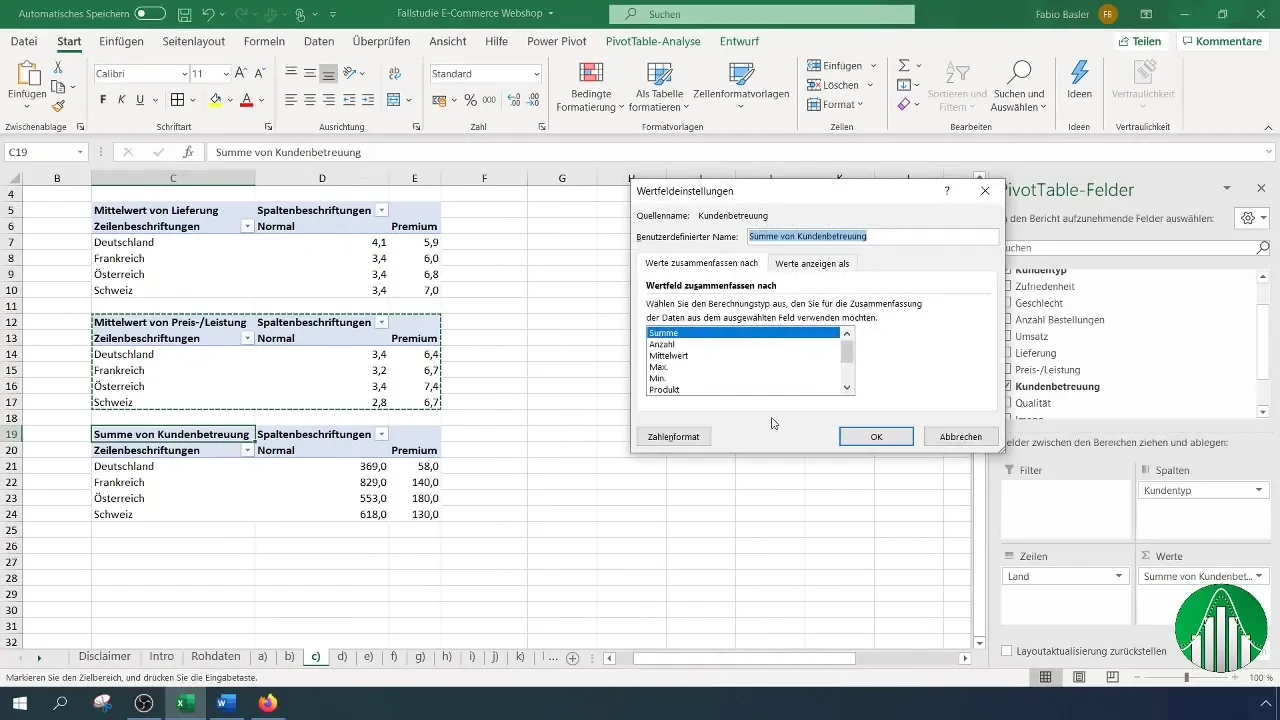
Quando aggiungi i successivi indicatori, copia e adatta le tabelle di conseguenza. Questo ridurrà il lavoro e aumenterà la coerenza dei tuoi calcoli.

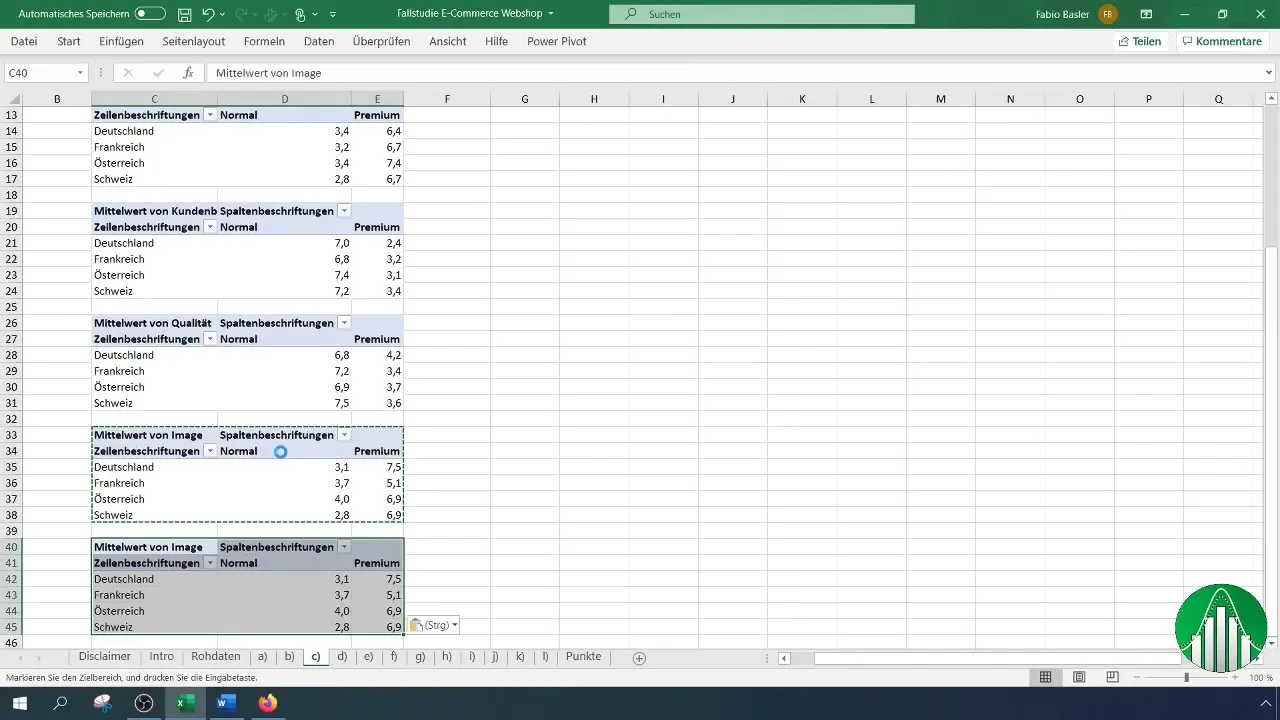
Passo 4: Calcolare la variazione relativa

Per calcolare la variazione relativa, in particolare per "Innovazione", sposteremo leggermente la tabella esistente. Clicca sulle impostazioni della tabella pivot e cambia il valore da "Media" a "Deviazione standard". Questo ti darà un'idea di come variano le valutazioni.

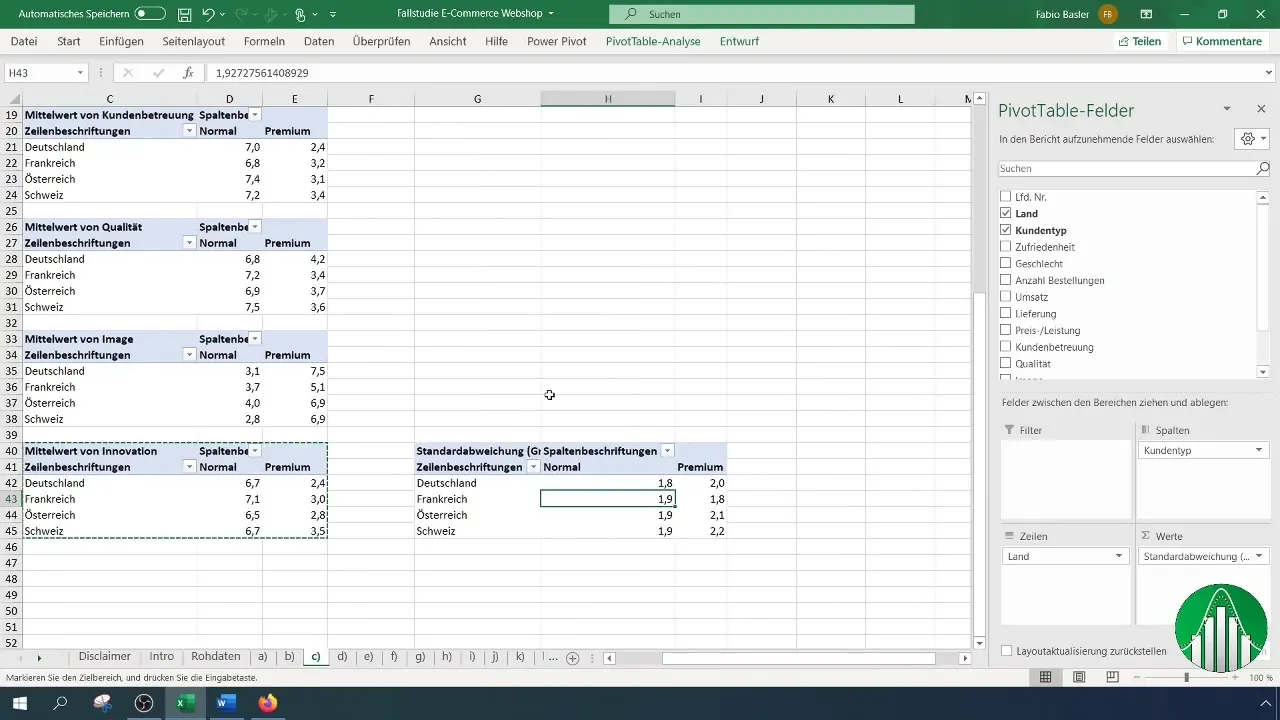
Adesso calcolerai la variazione relativa inserendo il coefficiente di variazione in una nuova colonna in modo formulare. Utilizza la deviazione standard e il valore medio per il tuo calcolo.

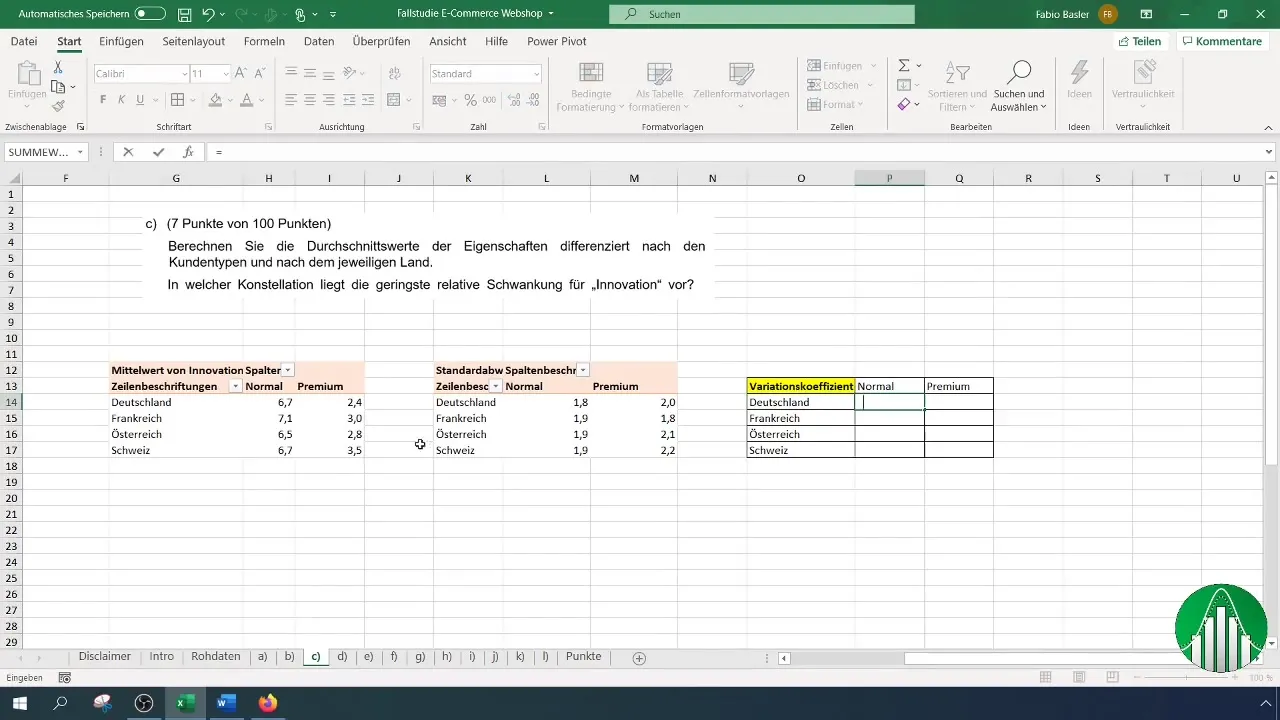
È importante specificare correttamente i riferimenti delle celle in modo che Excel possa calcolare i valori corrispondenti.

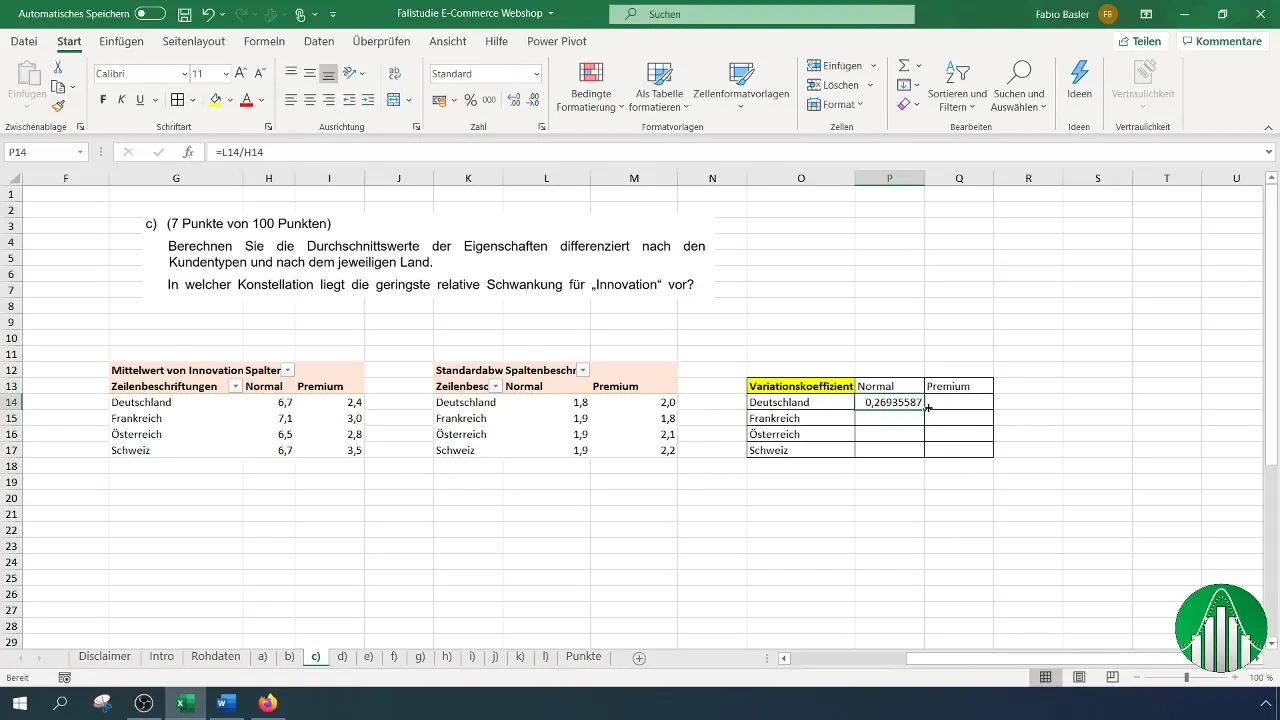
Passo 5: Tabella di supporto e interpretazione

Crea una tabella di supporto per la variazione relativa. Definisci ad esempio tre classi: bassa, media e alta variazione relativa. Inserisci i valori calcolati qui per facilitarne l'interpretazione.

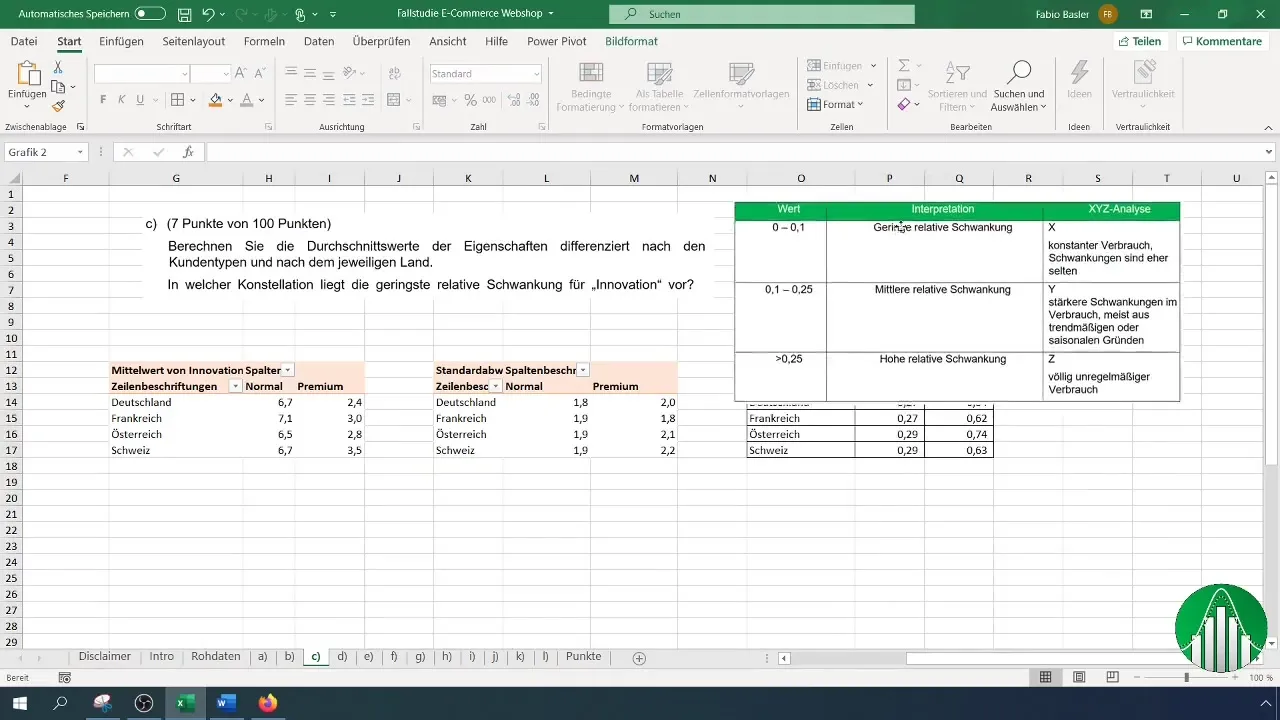
Utilizza la formattazione condizionale per evidenziare visivamente i valori. Una scala di colori può aiutarti a capire rapidamente quali risposte presentano un'ampia variazione.

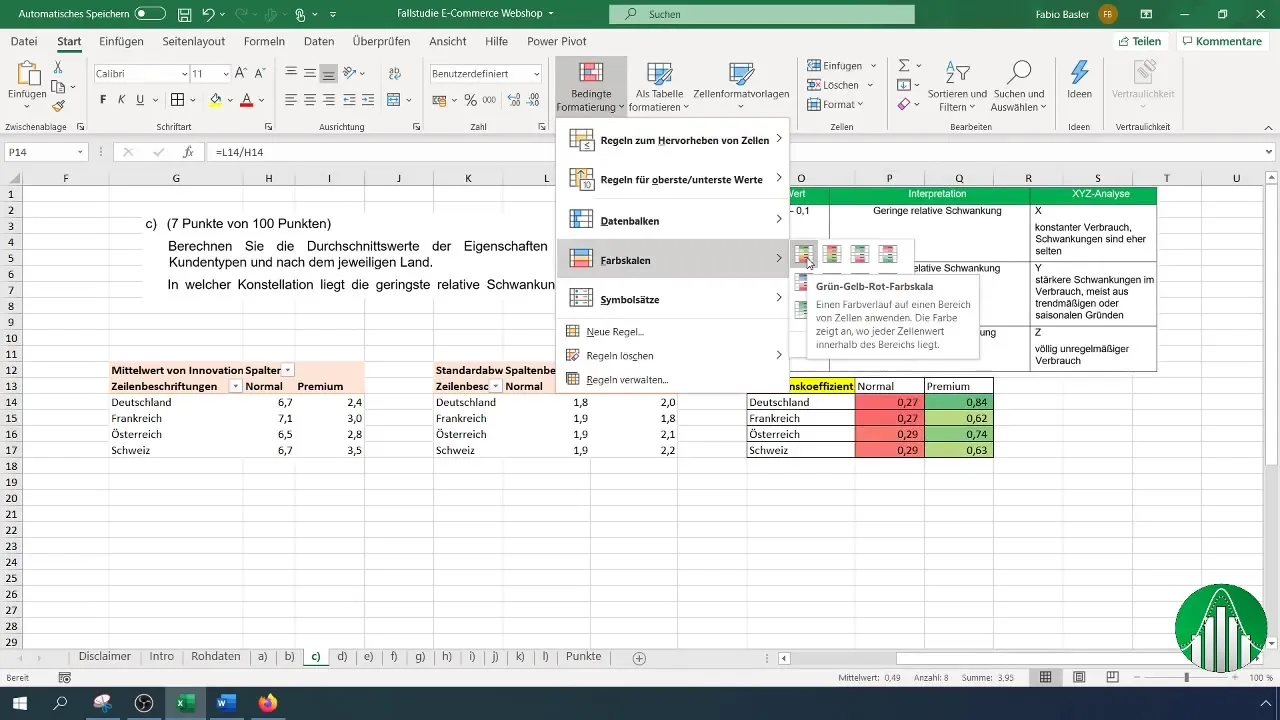
Passaggio 6: Riassumere i risultati

Dopo aver creato tutti i dati chiave, riassumi i tuoi risultati. Formula risposte chiare alle principali scoperte alla luce della tua analisi.

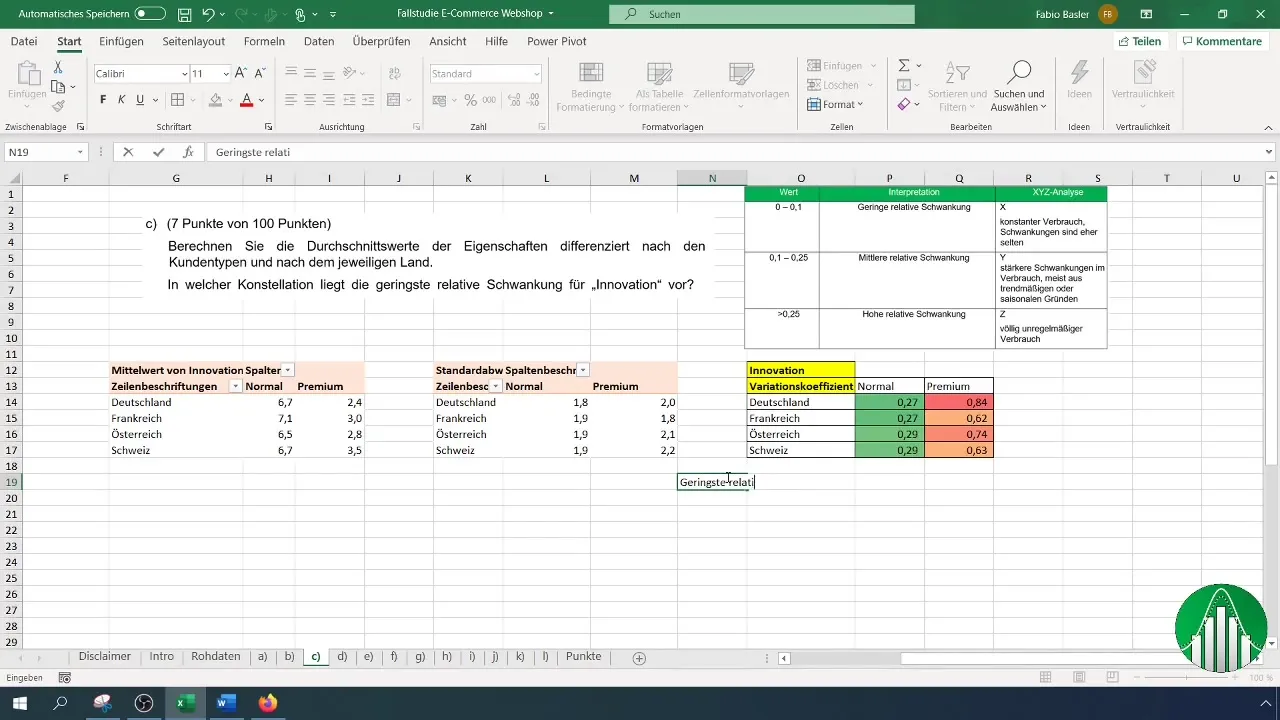
Assicurati di includere tutti i punti chiave, come l'escursione relativa minima e massima, nonché i valori medi. Questo ti fornirà una chiara panoramica dei tuoi dati e della loro interpretazione.

Riepilogo

In questa guida hai imparato come creare in modo efficace tabelle pivot multidimensionali in Excel per analizzare i dati dei sondaggi. Hai calcolato i valori medi e identificato l'escursione relativa dei risultati.