Distribuzione normale in Excel - Calcolare semplicemente le probabilità

La distribuzione normale è un concetto centrale della teoria della probabilità e statistica. In ogni insieme di dati distribuiti in modo uniforme, osserviamo la cosiddetta curva a campana, che compare spesso in sondaggi e analisi di vendite. In questo tutorial imparerai come calcolare e visualizzare la distribuzione normale per un sondaggio utilizzando Excel, per determinare probabilità cruciali. Con queste capacità non solo potrai comprendere meglio i tuoi dati, ma potrai anche utilizzarli in modo mirato per prendere decisioni informate.

Principali conclusioni

• Imparerai il calcolo passo dopo passo della distribuzione normale in Excel.
• Saranno mostrate le possibilità della rappresentazione grafica di una distribuzione normale.
• Capirai come calcolare le probabilità per eventi specifici.

Guida passo passo

Prima di tutto, assicurati che tutti i dati necessari siano presenti in una tabella Excel. Questi dati potrebbero rappresentare ad esempio i ricavi di un sondaggio.

Visualizzazione della distribuzione normale

Per visualizzare graficamente la distribuzione normale dei ricavi, procedi come segue:

Prima di tutto seleziona i dati dei ricavi nella tua tabella Excel e copiali in una nuova colonna. Nella barra dei menu fai clic su "Inserisci" e scegli "Grafico". Qui opta per un istogramma per rappresentare visivamente la distribuzione. Puoi scegliere un istogramma vuoto per mostrare i valori standard dei tuoi dati.

Fai clic con il pulsante destro del mouse sul grafico e seleziona "Seleziona dati". Nella finestra che si apre aggiungi i tuoi dati dei ricavi come prima serie di dati. Nell'elenco dei valori di riga seleziona tutti i set di dati tenendo premuto il tasto Shift e selezionando i valori.

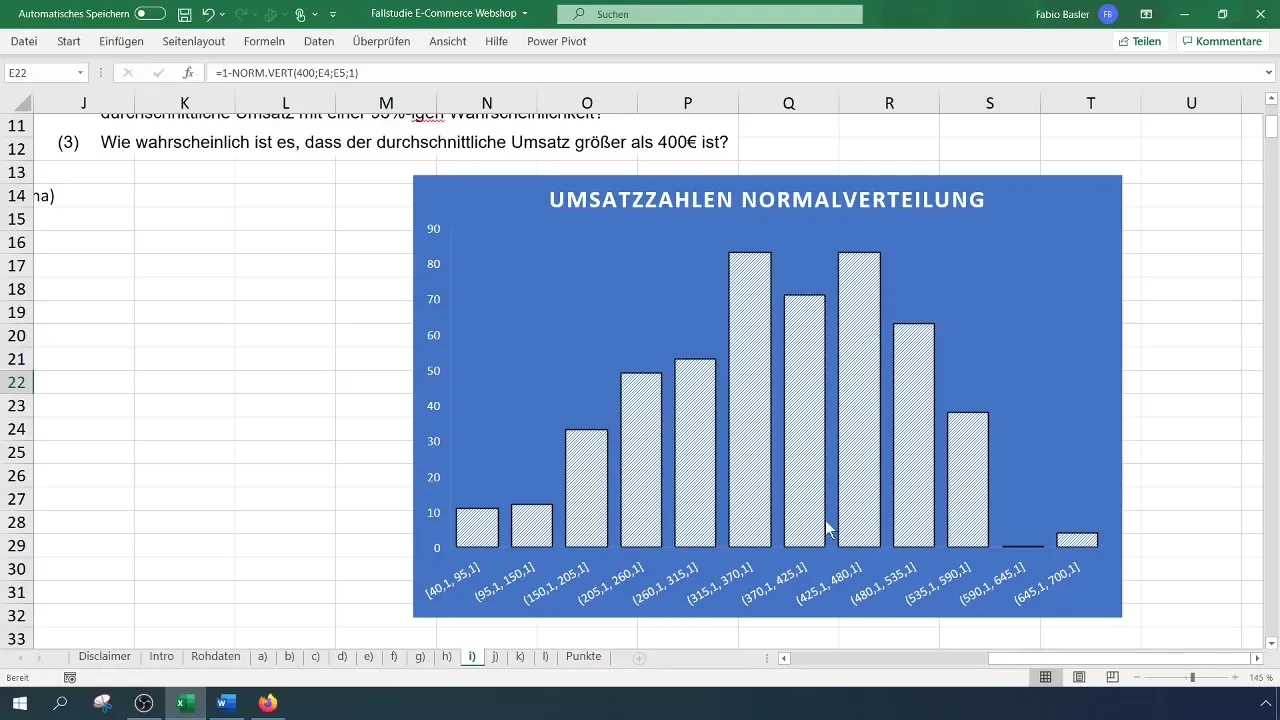
Una volta visualizzati i dati nell'istogramma, puoi personalizzare il titolo del grafico per renderlo più rappresentativo. Ad esempio, cambia il titolo in "Distribuzione normale dei ricavi". Assicurati che la curva a campana sia riconoscibile; ciò indica una distribuzione normale.

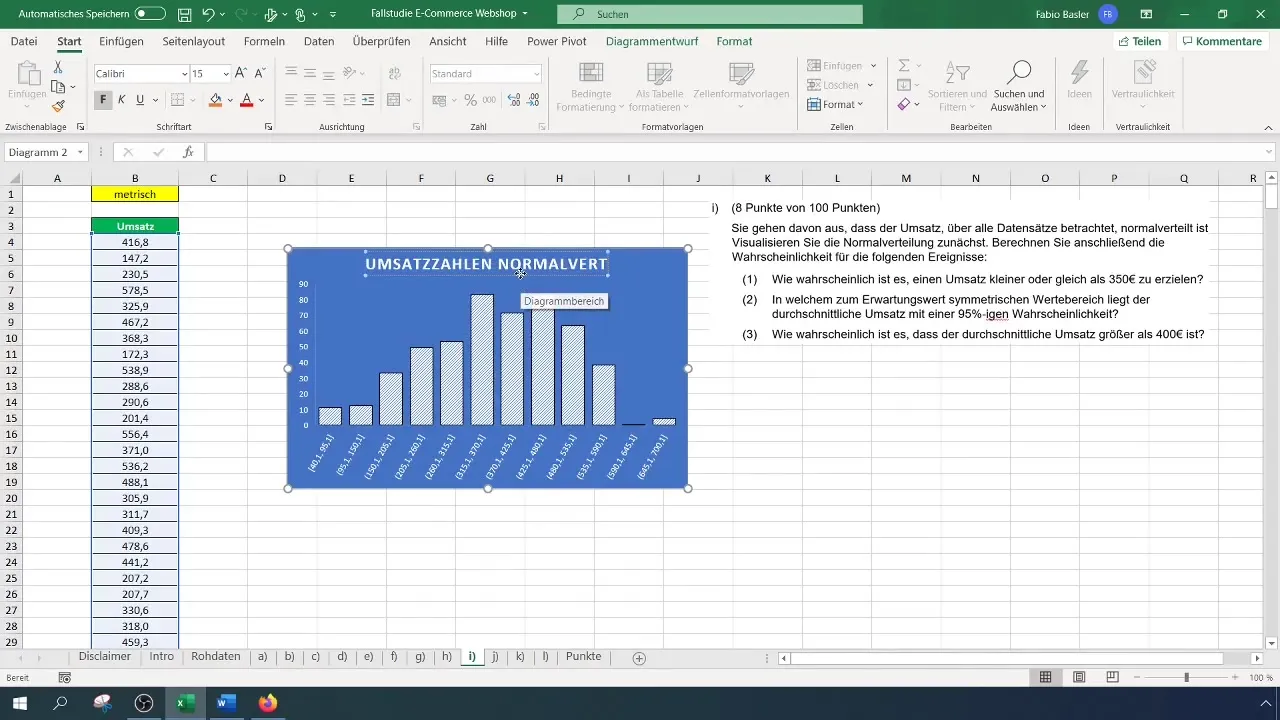
Calcolo delle probabilità

Il prossimo compito è determinare la probabilità che i ricavi siano inferiori o uguali a 350 euro. Per fare ciò, avrai bisogno della media e della deviazione standard dei dati dei ricavi.

Per calcolare la media, utilizza la formula =MEDIA(A1:A100) (dove A1:A100 sostituisce l'effettivo intervallo di dati). Nel tuo esempio, ciò potrebbe risultare in una media di ricavi di 369 euro.

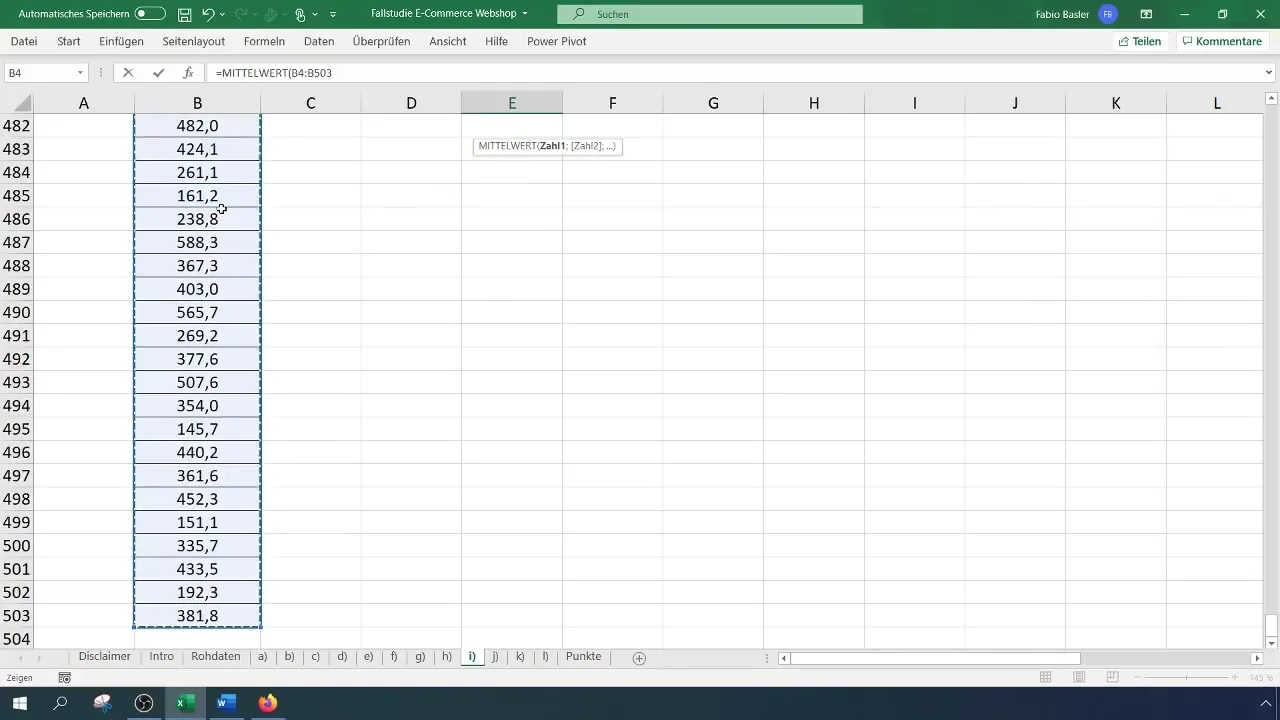
Per la deviazione standard, utilizza la formula =DEV.ST(A1:A100), che potrebbe risultare in circa 124,12 euro nel tuo caso.

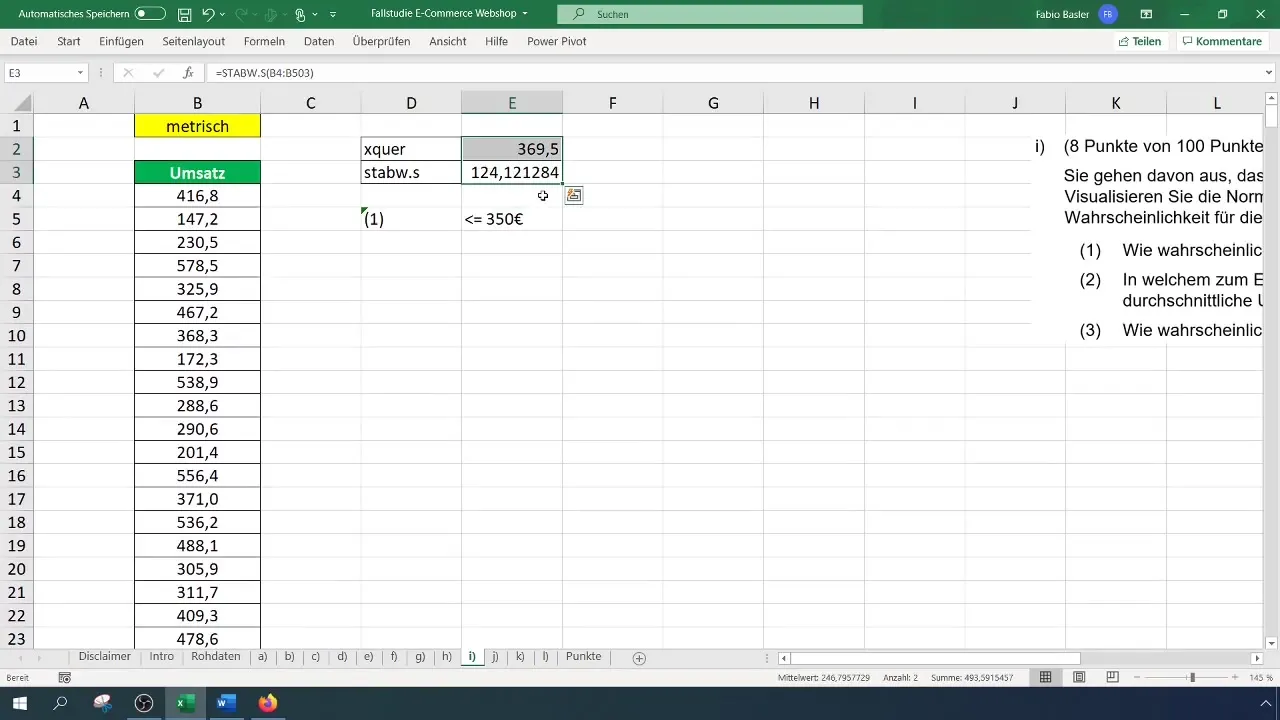
Ora puoi calcolare la probabilità per un ricavo di 350 euro. Ciò avviene attraverso la formula: =NORM.DIST(350; Media; Deviazione standard; VERO). Inserisci i valori corrispondenti e premi Invio.

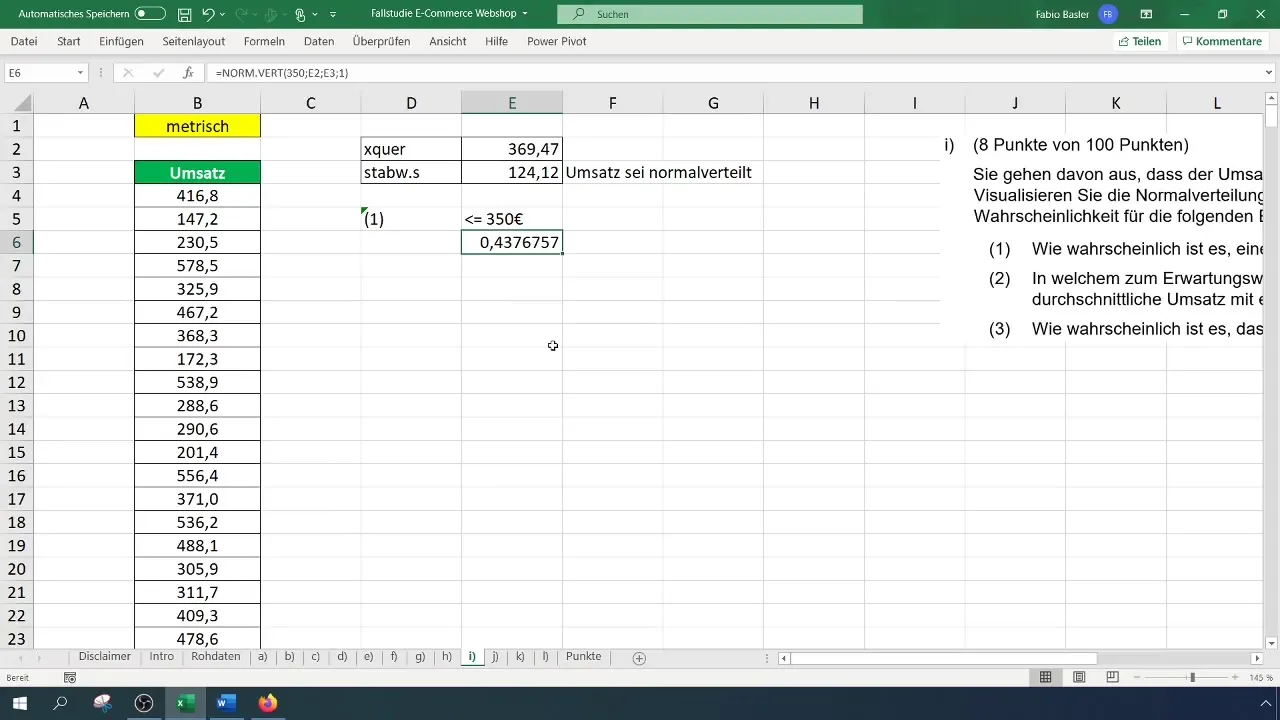
Il risultato di questo calcolo potrebbe mostrarti che la probabilità di ottenere un ricavo inferiore o uguale a 350 euro è di circa il 43,8%. Per illustrare ciò, formatta i valori e passa alla rappresentazione percentuale.

Calcolo del range di valori simmetrici intorno al valore atteso

Il prossimo obiettivo è determinare il range di valori simmetrici intorno al valore atteso con una probabilità del 95%. Per fare ciò, devi trovare il valore quantitativo per il 95%.

Questo avviene inserendo la formula =NORM.INV(0,95) in una cella, che ti restituirà il valore del quantile di 1,65.

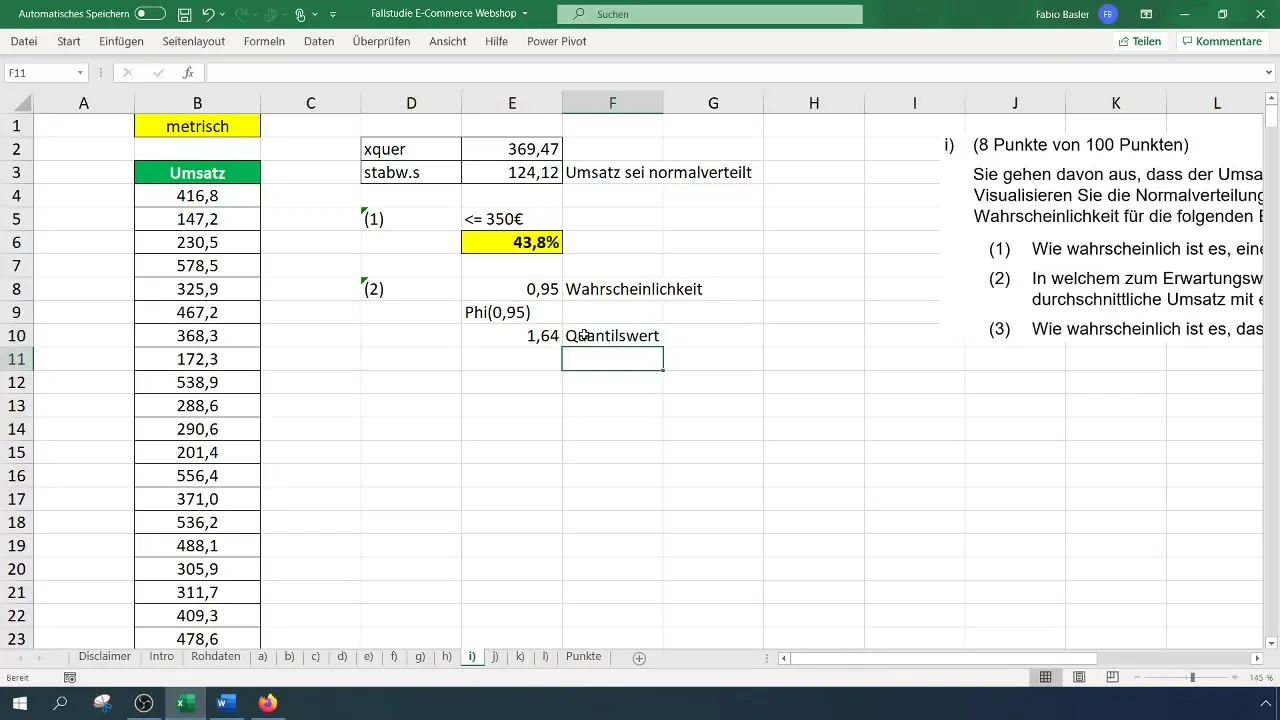
Ora inserisci questo calcolo in un'equazione per trovare il range di valori. La formula potrebbe essere simile a: Valore atteso + (Deviazione standard * Valore del quantile). Inserisci i valori corrispondenti e calcola il range di valori simmetrici.

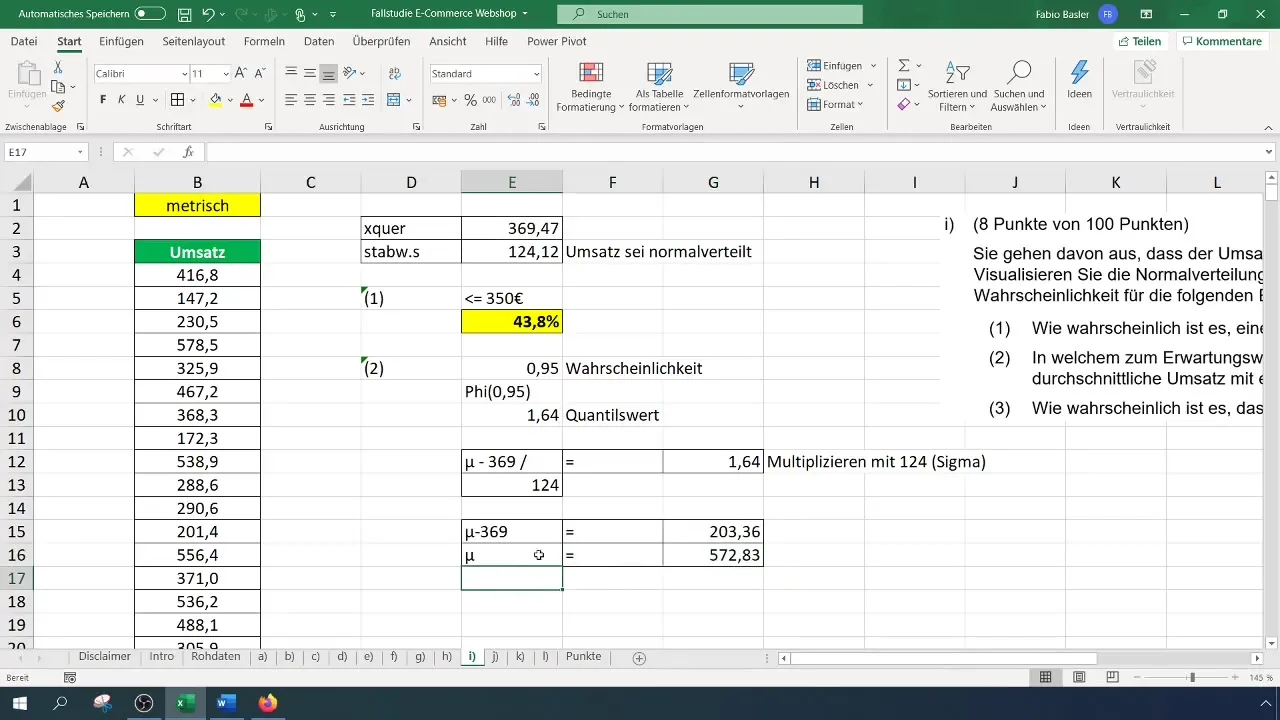
Se ad esempio ricevi un valore di 572 euro, ciò significa che puoi aspettarti un fatturato all'interno di questo intervallo con una probabilità del 95%.

Probabilità di fatturati più alti

Per l'ultima calcolazione determinerai la probabilità che il fatturato sia superiore a 400 euro. A tal fine è necessario utilizzare la formula =1 - NORM.DIST(400; Media; Deviazione standard; VERO).

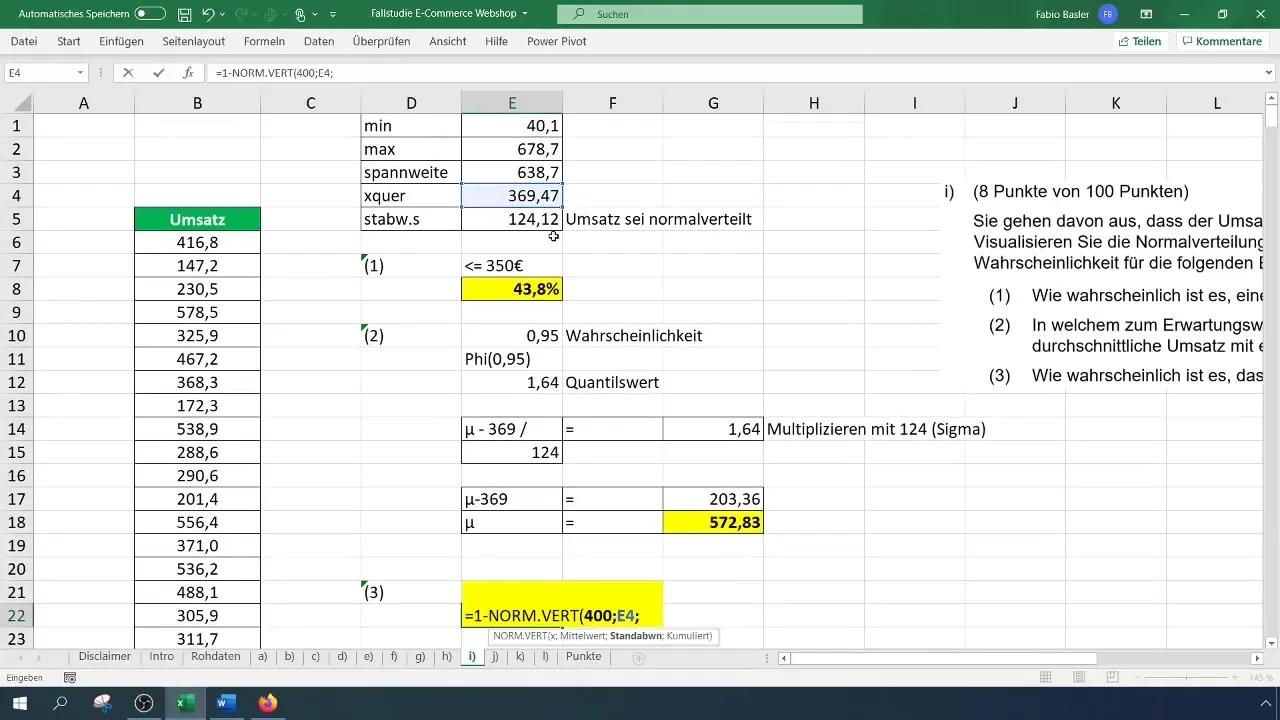
Anche in questo caso la probabilità potrebbe essere del 40%. Questi valori sono sensati da mettere in discussione. Osservando la scala nell'istogramma, è possibile verificare la coerenza del percentuale di fatturati più alti.

Riepilogo

In questa guida hai imparato come utilizzare la distribuzione normale in Excel per calcolare le probabilità. Basandoti su esempi pratici da un sondaggio, hai imparato come gestire i dati sia graficamente che calcolando. La comprensione di questi concetti ti aiuterà a implementare con successo analisi statistiche nei tuoi progetti.