データの分析に取り組む際、さまざまな変数間の関係を認識する必要があることにすぐ気づくでしょう。このチュートリアルでは、Excelを使用して2つの名義尺度変数間の関係を数量化する対応分析を行う方法を紹介します。自動車部品産業の実践例を用いて、データからどのように有益な洞察を得るかを理解します。
重要な洞察
- 対応分析により、2つの名義尺度変数間の関係を調査できます。
- 対応係数は関係の強さを量的に表します。
- Excelのピボットテーブルは分析に欠かせないツールです。
対応分析の手順
ステップ1: データの準備
Excelで対応分析を開始する前に、作業するデータが適切に整形されていることを確認する必要があります。すべてのフィルタ設定を削除して、データ全体を見ることができるようにします。
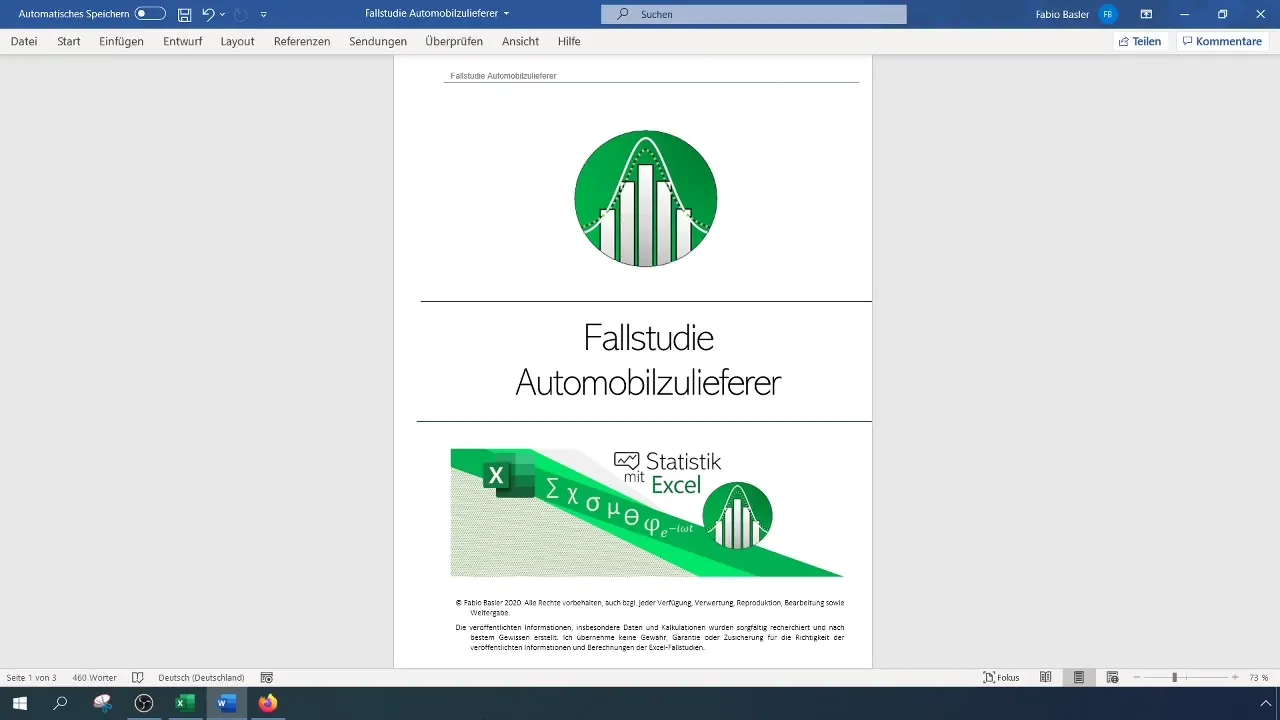
名義尺度データとして、生産責任者および不適合情報を含む概要を作成します。この例では、A、B、C組長に焦点を当て、他の代表を排除します。
ステップ2: ピボットテーブルの作成
対応分析を行うには、生産責任者と不適合の各組み合わせがどれだけ頻繁に発生するかを示す2次元的な頻度分布を作成する必要があります。「挿入」メニューに移動し、「ピボットテーブル」を選択します。
該当するデータ範囲を選択し、見出しを正しく認識することを確認します。ピボットテーブルが作成されると、生産責任者と不出品を対比することができます。
ステップ3: 頻度の分析
ピボットテーブルを作成した後、絶対頻度を特定できます。ピボットテーブルの行と列に特徴を配置します。これにより、各組長の不出品がどれくらいあるかがわかります。
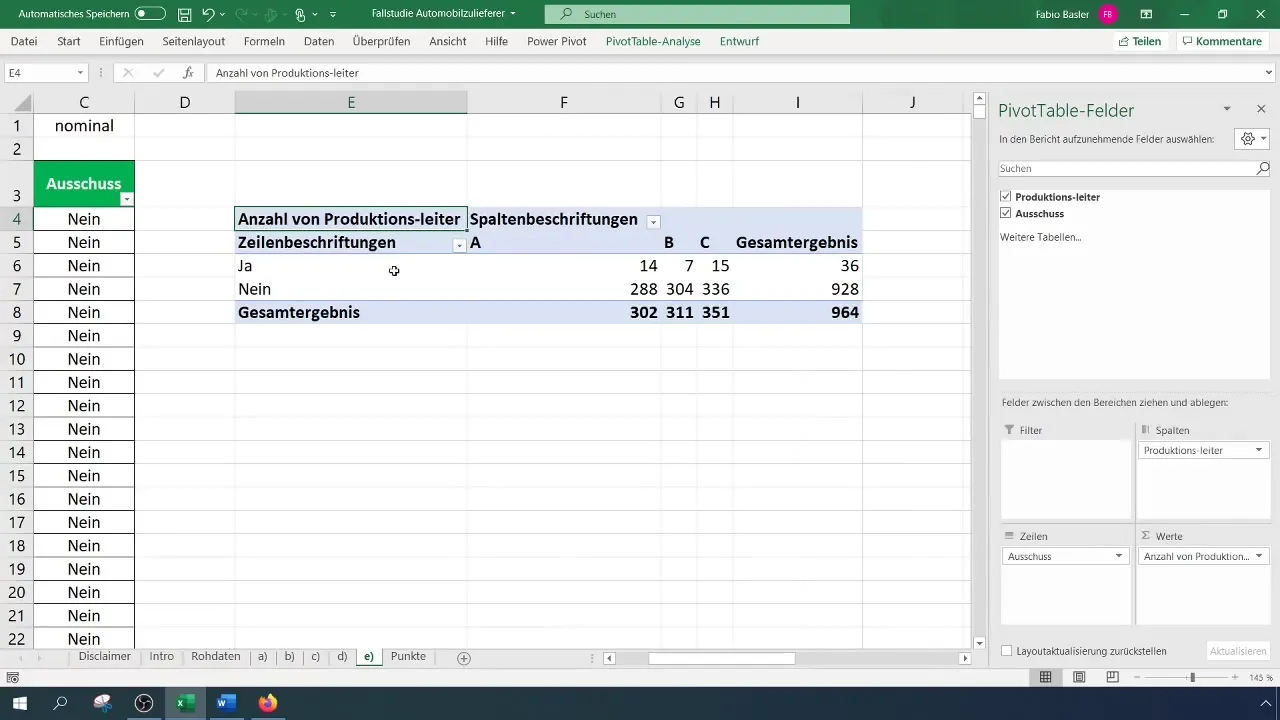
ピボットテーブルを確認し、結果を分析してください。特に変数の分布に注意して、どの組長で不出品が最も頻繁または最もまれに発生するかを調べます。
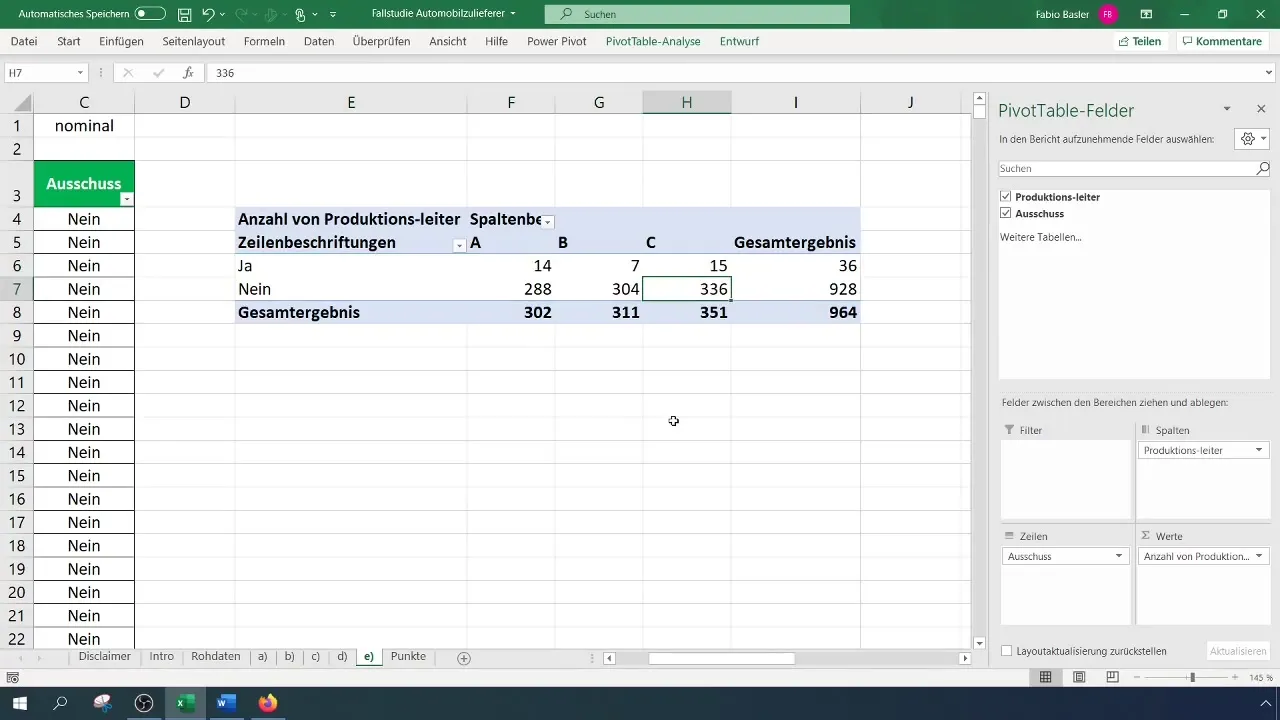
ステップ4: 期待頻度の計算
対応係数を計算するために、期待される絶対頻度を決定する必要があります。一般的な式は次の通りです: (N_{ij} = \frac{(R_i \times C_j)}{N})。ここで、(R) は行の周辺頻度、(C) は列の周辺頻度を表します。
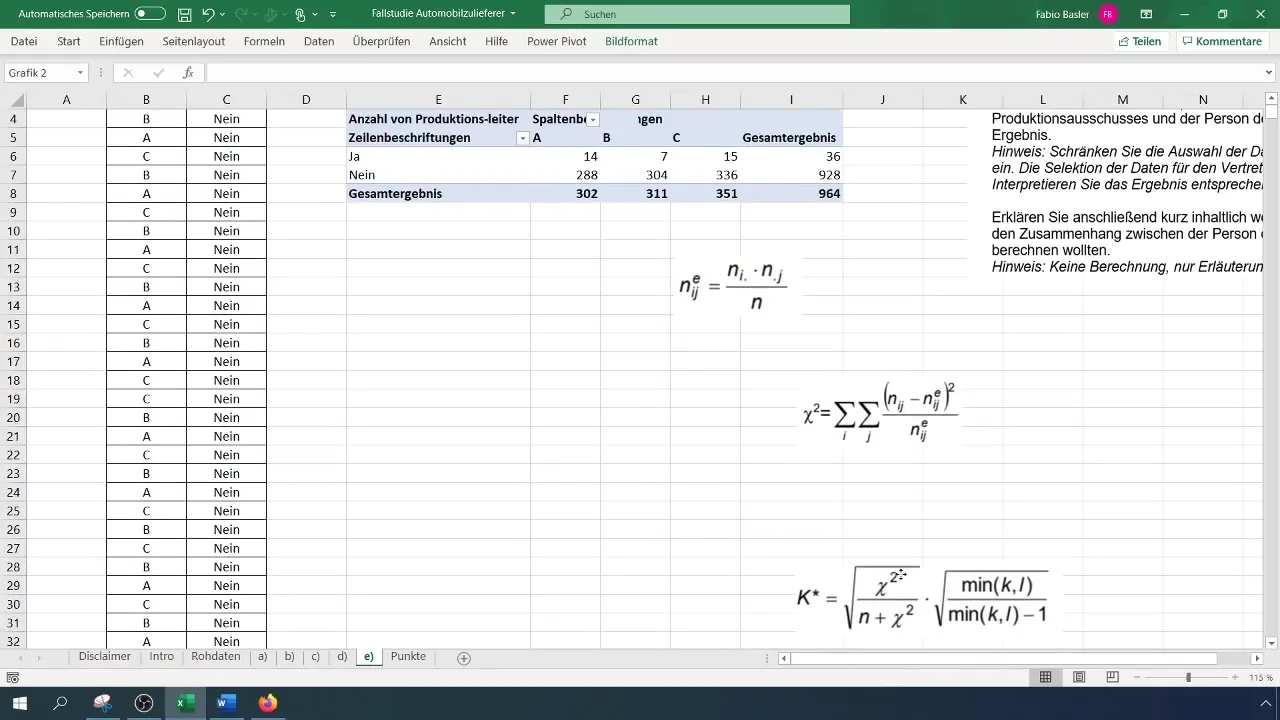
ピボットテーブルの値にこの計算を適用します。予想頻度のために別のテーブルを作成して、分析を整理します。
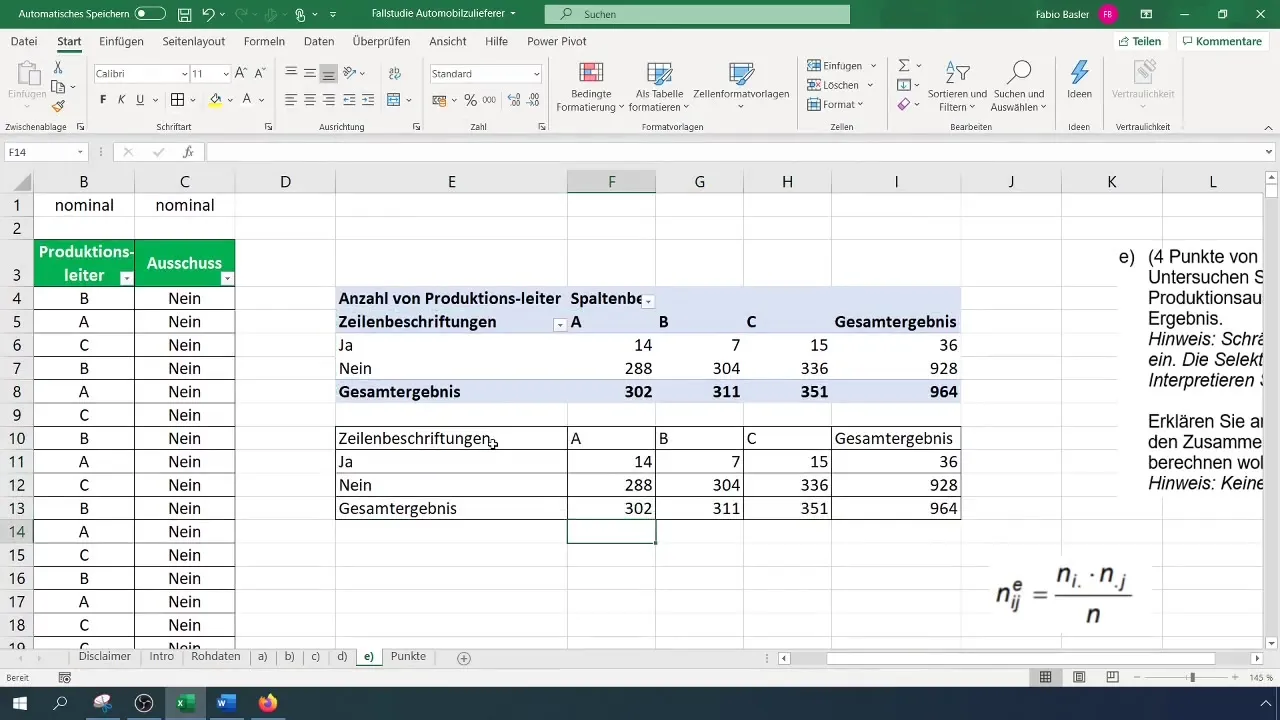
ステップ5: カイ二乗値の計算
変数間の関係を定量的に捉えるために、カイ二乗値を計算します。式は以下の通りです:
[ \chi^2 = \sum \frac{(O{ij} - E{ij})^2}{E_{ij}} ]
ここで、(O)は観測された頻度、(E)は予想された頻度です。
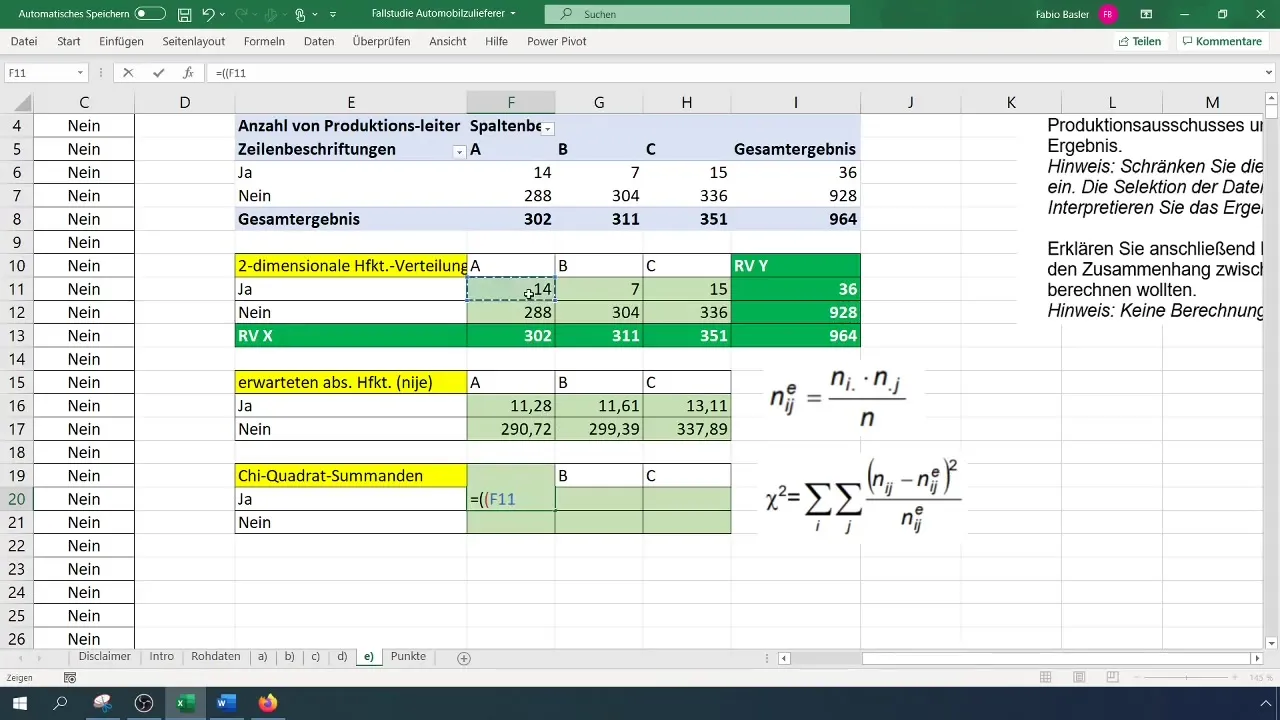
観測値と期待値の差の二乗を計算してください。
ステップ6: 対応係数の計算
最後のステップは、連関係数を計算することです。計算式は次の通りです:
[ K = \sqrt{\frac{\chi^2}{N}} ]
先に計算したχ二乗値と総観測数(N)を使用してください。
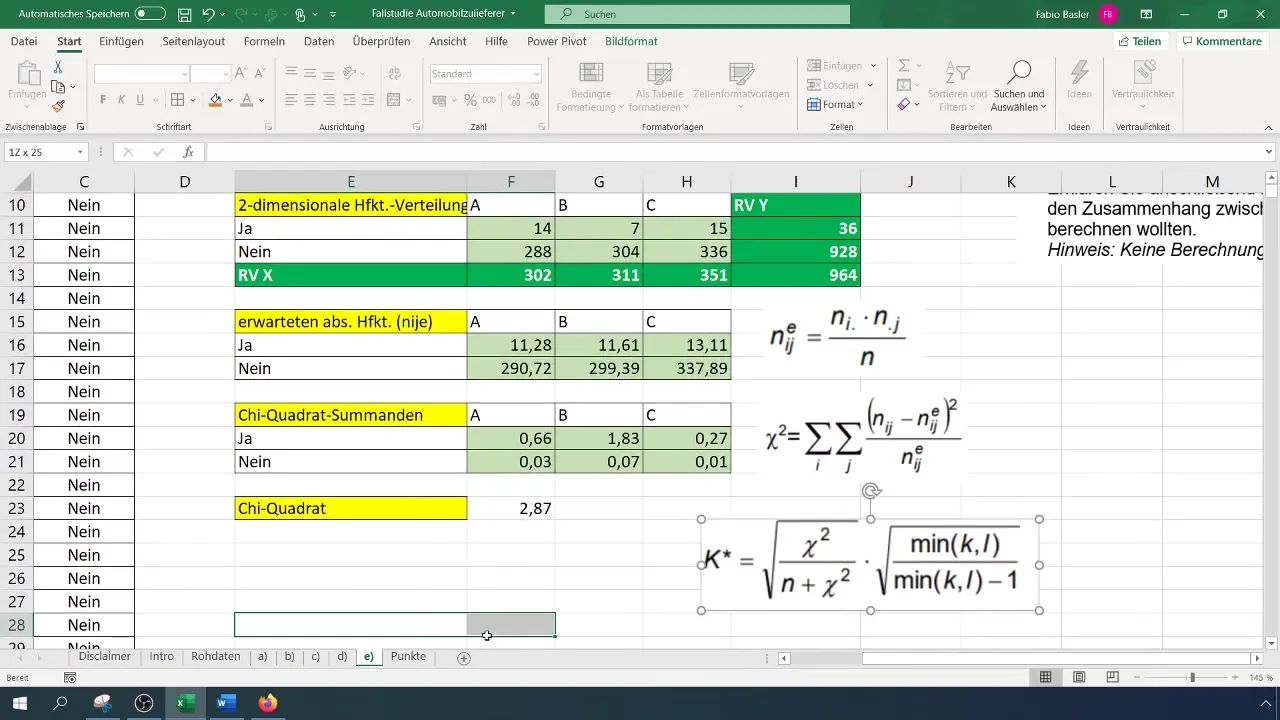
連関係数を計算した後、結果を解釈できます。この分析によると、0.077の連関係数は変数間の弱い関係を示しています。
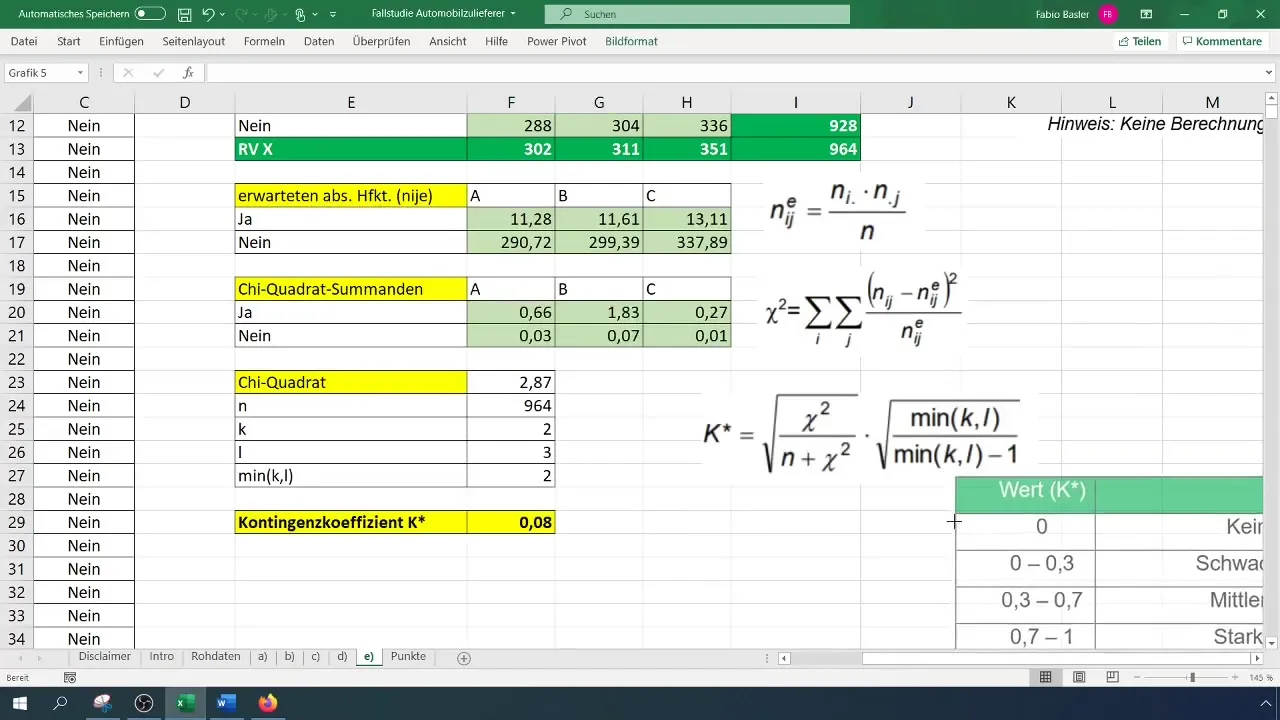
ステップ7:結果の解釈
分析の最後のステップは、結果を解釈することです。連関係数が0に近いと、変数間にほとんど関係がないことを示します。0.08の値は、生産管理者が不良品の発生に対して有意な影響を与えていないことを示しています。
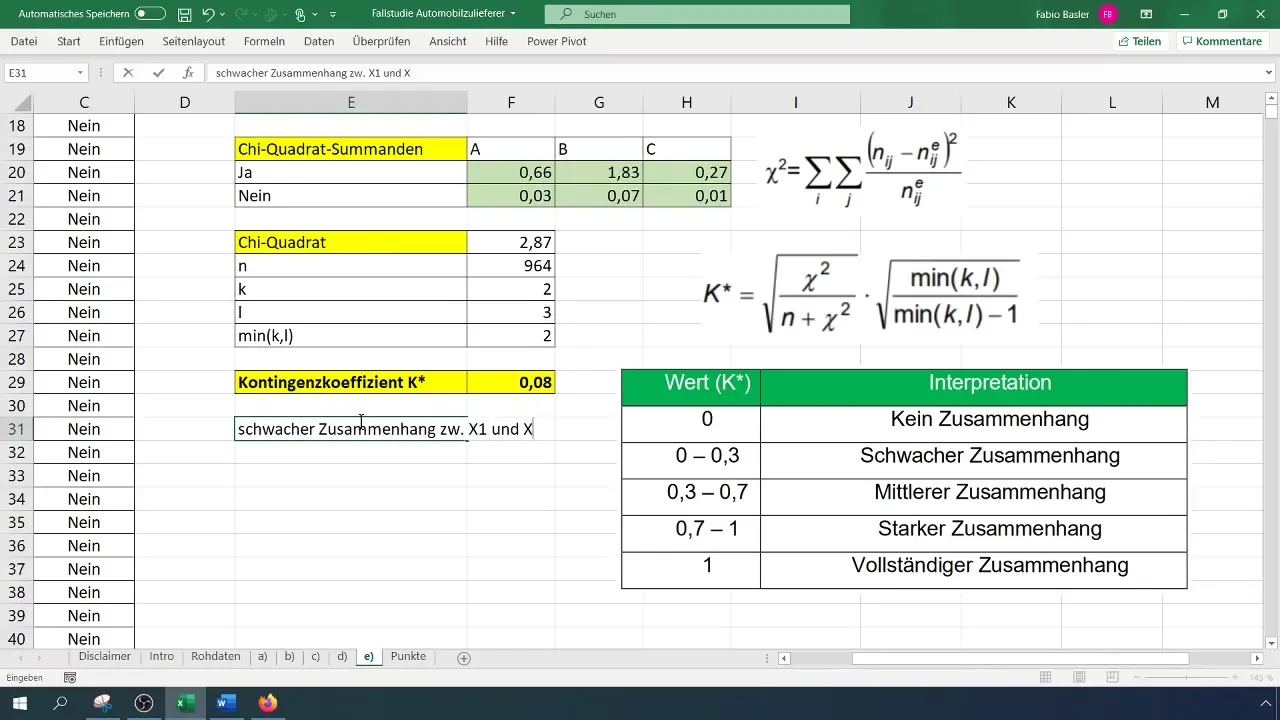
概要
このガイドでは、Excelでの連関分析を行う方法を学びました。名義尺度変数間の関係を認識するために、データの準備方法、ピボットテーブルの作成、および連関係数の計算に必要な手順を学びました。


