Excel で期待値の 1-SP テストが成功しました。

統計テストはデータ解析と意思決定の中核です。特にバイオテクノロジーの分野では、薬剤の成功率に関する仮説を検証することが重要です。このチュートリアルでは、Excelで既知の分散を持つ期待値の単一標本テスト（1-SP-Test）を効率的に実施する方法を学びます。

重要な知見

このガイドでは、以下の内容を紹介します:

• 1-SP-Testの理論的基礎。
• Excelでのテストの実施手順。
• 結果の解釈。

データの準備

Excelで1-SP-Testを実施するには、まず関連するデータが必要です。この例では、薬剤の成功率を分析する状況を想定しています。以前の平均成功率が59%で、標準偏差が19であることが分かっています。まずは、データをExcelのテーブルに入力してください。

後でデータにアクセスできるように、データが列に整理されていることを確認してください。見やすく整理されていると、各ステップを追いやすくなります。

テストの概要

1-SP-Testは、平均成功値が与えられた値と有意に異なるかどうかを検証するためのものです。この場合、59%の成功率が将来的に著しく向上できるかどうかを検証します。

仮説の立て方

テストのために立てる仮説は重要です:

• 帰無仮説（H0）: 真の期待値は59と等しい（σ = 59%）。
• 対立仮説（H1）: 真の期待値は59%よりも大きい。

仮説を立てる際に焦点を当てるべきは、何を具体的にテストするか、あなたの文脈での背景をどのように表すかです。

帰無仮説と対立仮説の違いを明確に認識することは重要です。これらは後続の計算の基礎となります。

標本の収集

テストで500の薬剤の標本を取得します。標本の選択が代表的であり、結果を全体集団に現実的に適用できるよう適切な方法で保証されていることが重要です。

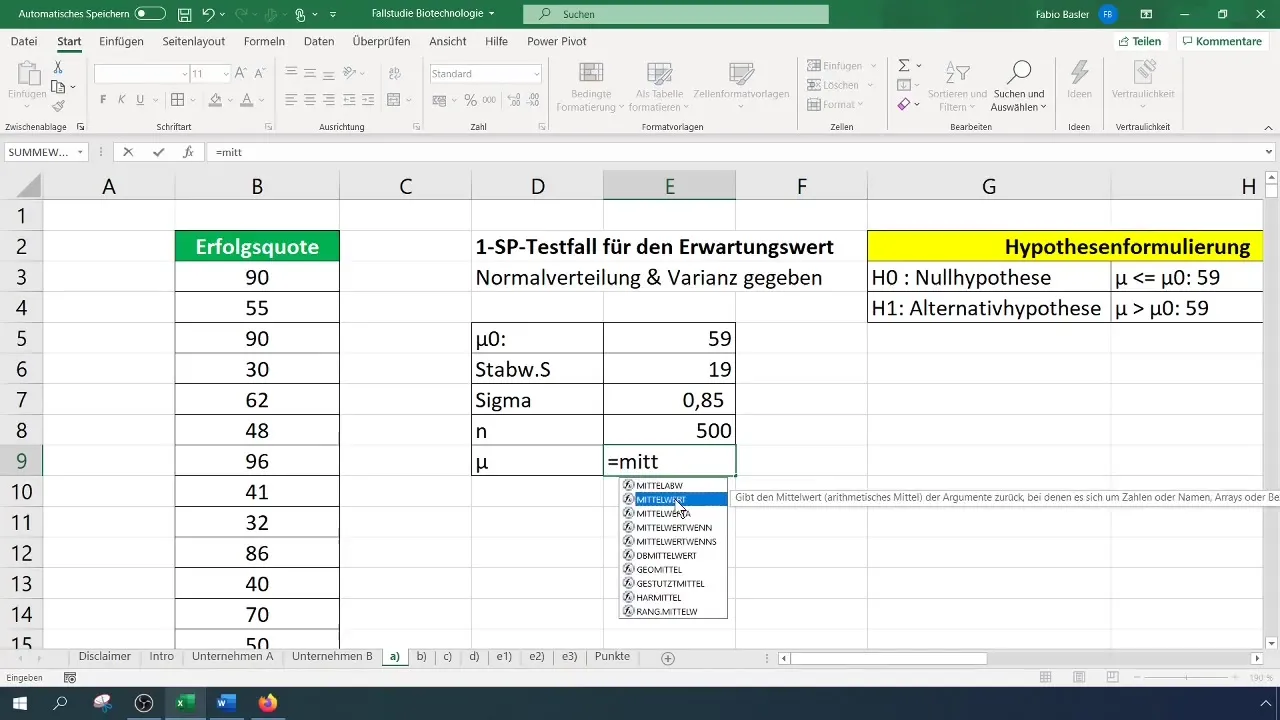
テストのためにまず算術平均を計算します。この作業は、Excelで適切な数式を使用することで簡単に行うことができます。

検定統計量の計算

1-SP-Testの検定統計量は次の式で決定されます:

[ Z = \frac{\bar{x} - \mu_0}{\sigma/\sqrt{n}} ]

ここで、(\bar{x})は標本の平均値を、(\mu_0)は仮定された平均値（この場合59）、(\sigma)は標準偏差（ここでは19）、(n)は標本数（500）を表します。

数値を式に代入した後、検定統計量を計算して、それが有意かどうかを確認してください。

臨界値の決定

1%（0.01）の有意水準で臨界値を読み取るか計算する必要があります。この計算はExcelのNORM.S.INV機能を使用して行うことができます。

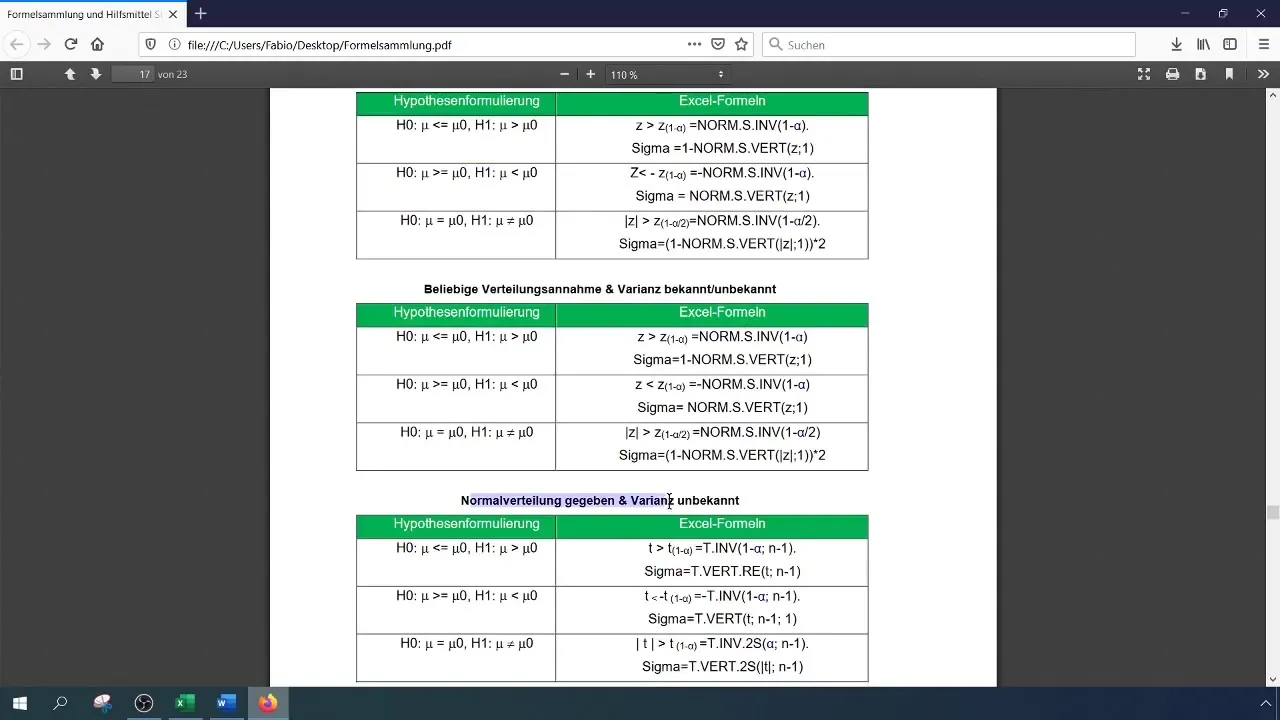
式は次の通りです:

[ \text{NORM.S.INV}(1 - \alpha) ]

ここで、(\alpha)は有意水準（0.01）です。求めた値は検定統計量と比較するための基礎となります。

テストの実施

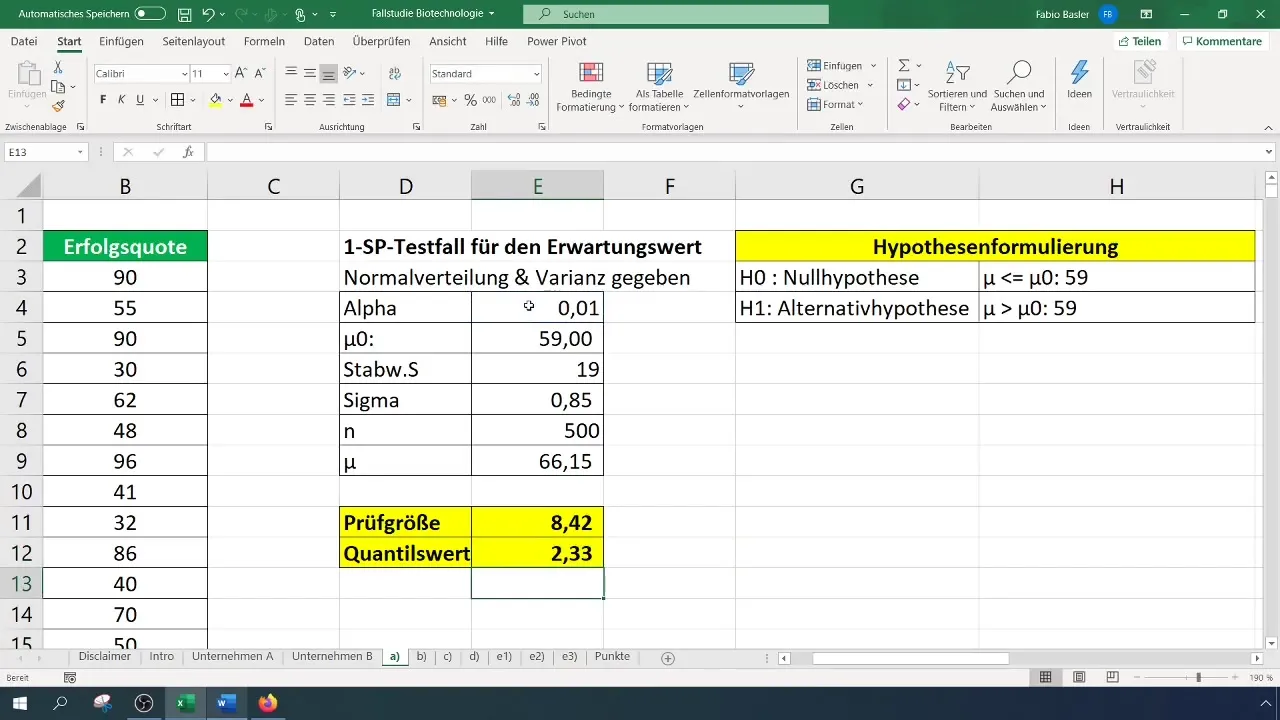
検定統計量と臨界値の両方を持つことで、次のように比較します:

• 検定統計量が臨界値よりも大きい場合、帰無仮説を棄却します。
• そうでない場合、帰無仮説を否定できません。

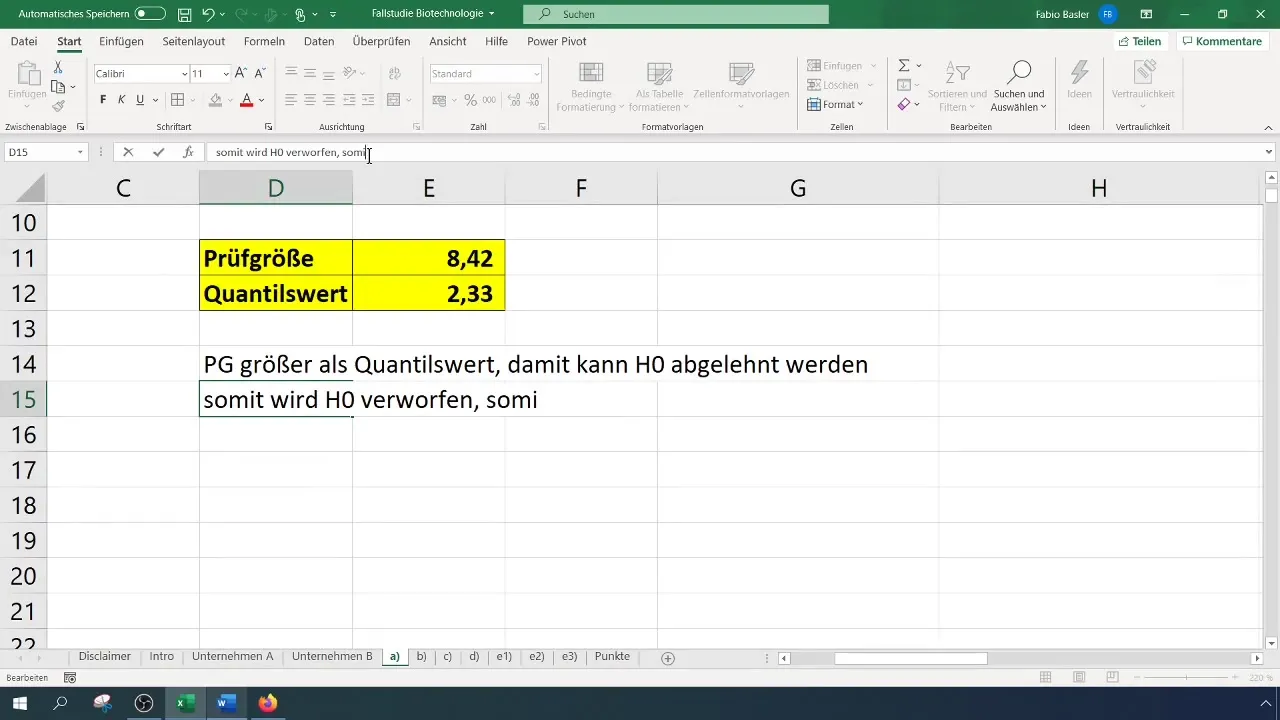
私たちの場合、検定統計量は8.4となり、臨界値2.33を超えています。したがって、帰無仮説を棄却することができます。これは成功率が有意に向上したことを示しています。

結果の解釈

テストを実行し、結果を得たら、それらを明確な文脈で解釈する必要があります。帰無仮説の拒絶は、検定された新しい値が過去の59%という場合と有意に異なることを意味します。

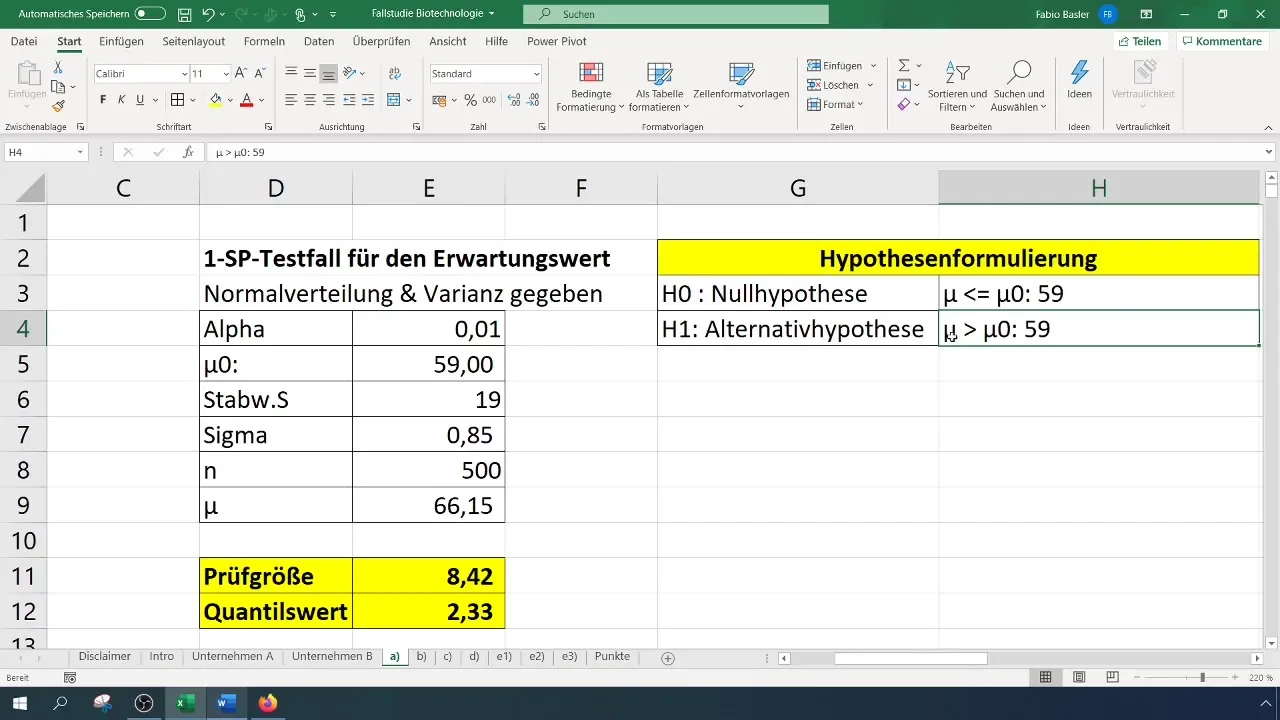
これらの情報は、企業の戦略的意思決定にとって非常に重要です。成功率を向上させる努力が効果的であることを確認しています。

要約

このチュートリアルでは、Excelで期待値の1-SPテストを実施する方法を学びました。ケーススタディを通じて、仮説構築からデータ計算、結果の解釈までのステップを追うことができました。これらの知識は、科学的評価だけでなく、企業での実用的な応用にも価値があります。