2標本t検定は、2つの平均値の違いを調査する際に統計学で重要なツールです。このチュートリアルでは、Excelを使用してこのテストを簡単かつ効果的に実行する方法を学びます。バイオテクノロジーの例を通じて、競合する2つの企業の成功率を比較し、統計的に分析する方法を学びます。
主な発見
- 2標本t検定の適用による2つの平均値の違いの分析。
- 仮説の策定と検証。
- Excelの使用による結果の計算と表示。
手順
まず最初に、Excelでのデータの作成とテストの実行を開始します。
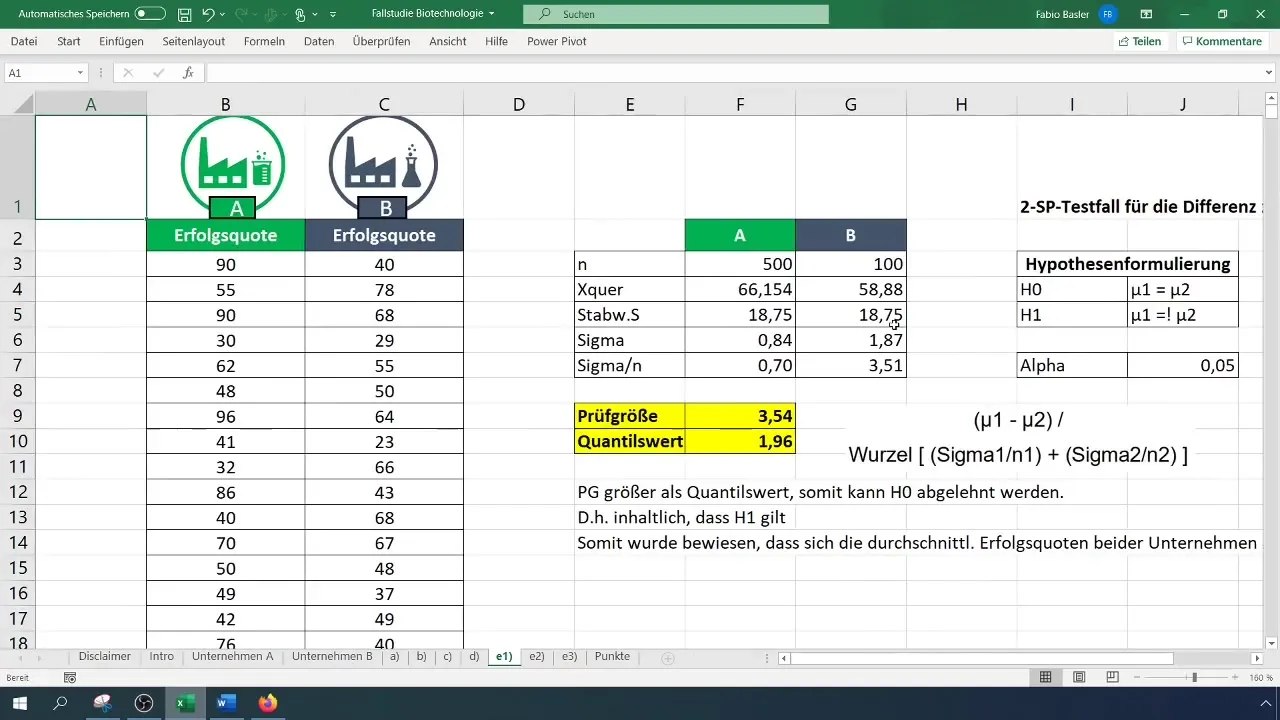
ステップ1:データ準備
2つの企業の成功率に関する生データを収集して始めます。企業AとBのデータを持っていると仮定します。各企業について100件のサンプルがあります。

ステップ2:標本のサイズと平均値を計算
Excelで表を作成して、標本とその平均値を対比します。まず、両企業の標本サイズ(N)と平均値(X)を計算します。

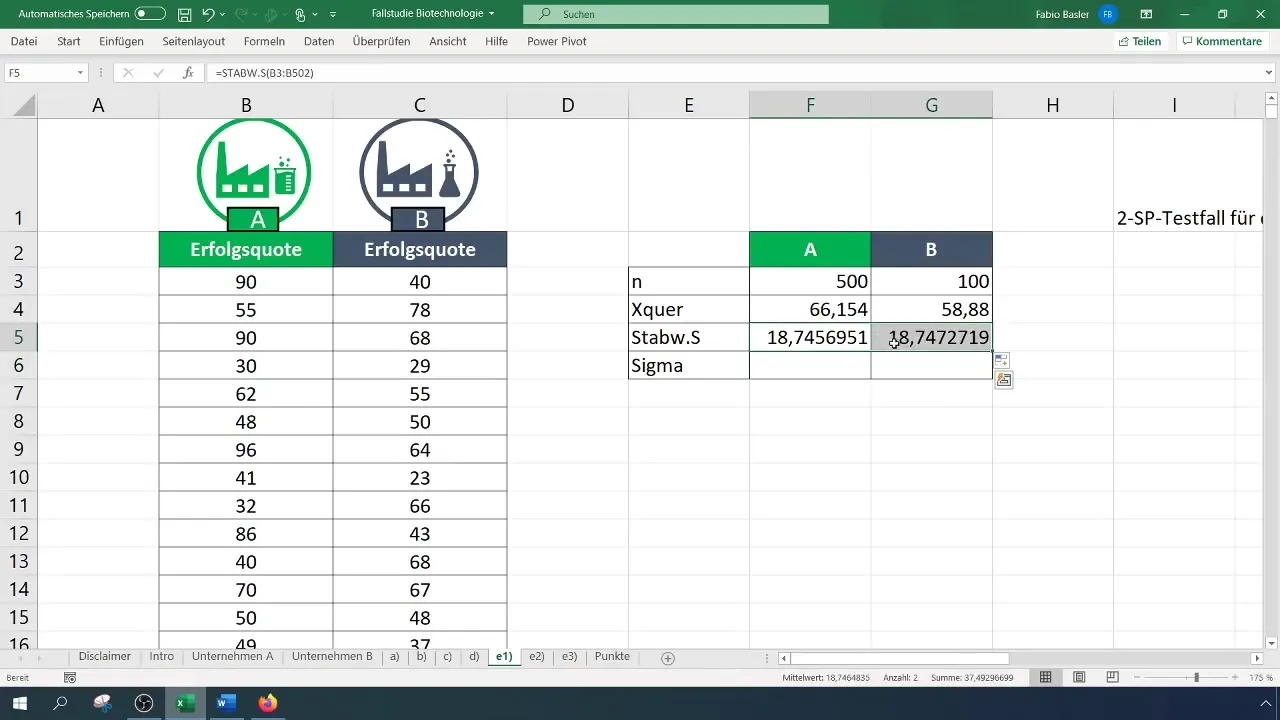
ステップ3:標準偏差の計算
両企業の標準偏差を計算します。これらの値は、分散とそれに続く計算を行うために重要です。
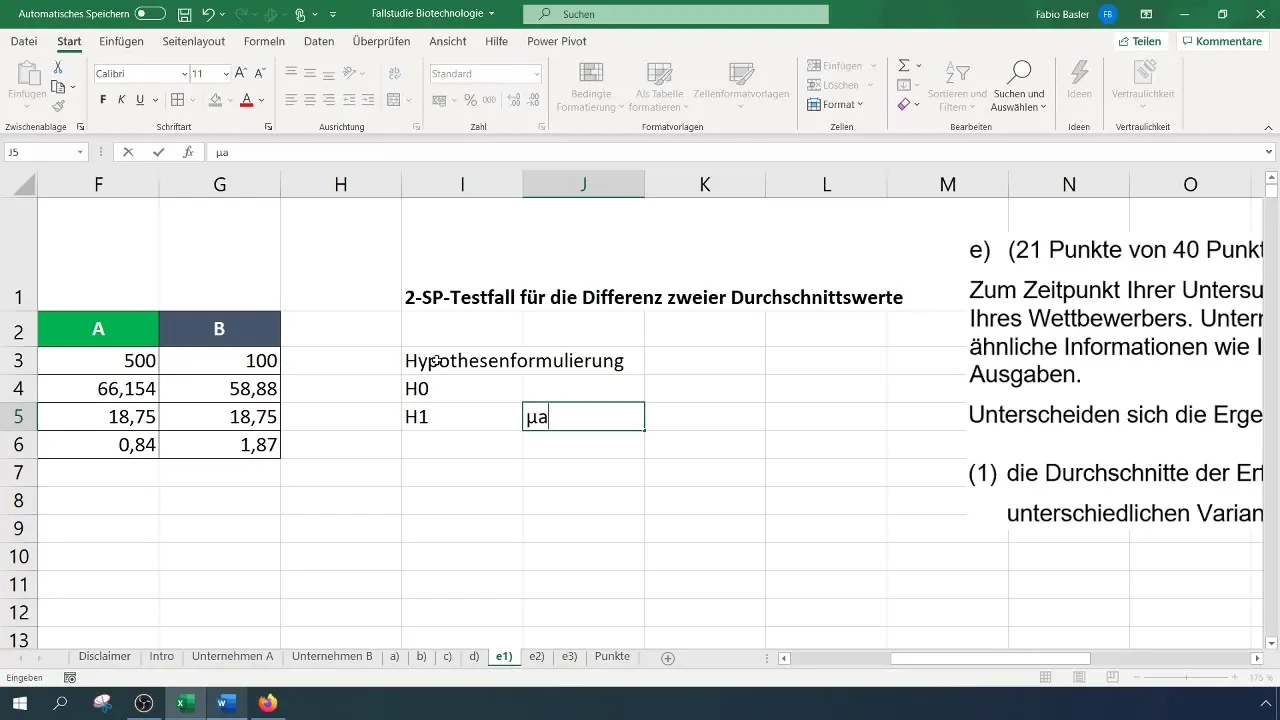
ステップ4:仮説の策定
帰無仮説(H_0)を立てます:企業AとBの成功率の平均値は等しいとする。対立仮説(H_1):成功率の平均値は異なるとする。
ステップ5:検定統計量の計算
検定統計量を計算するために、t-検定の式を使用します。平均値の差を計算し、サンプルごとの分散の合計の平方根で割ります。
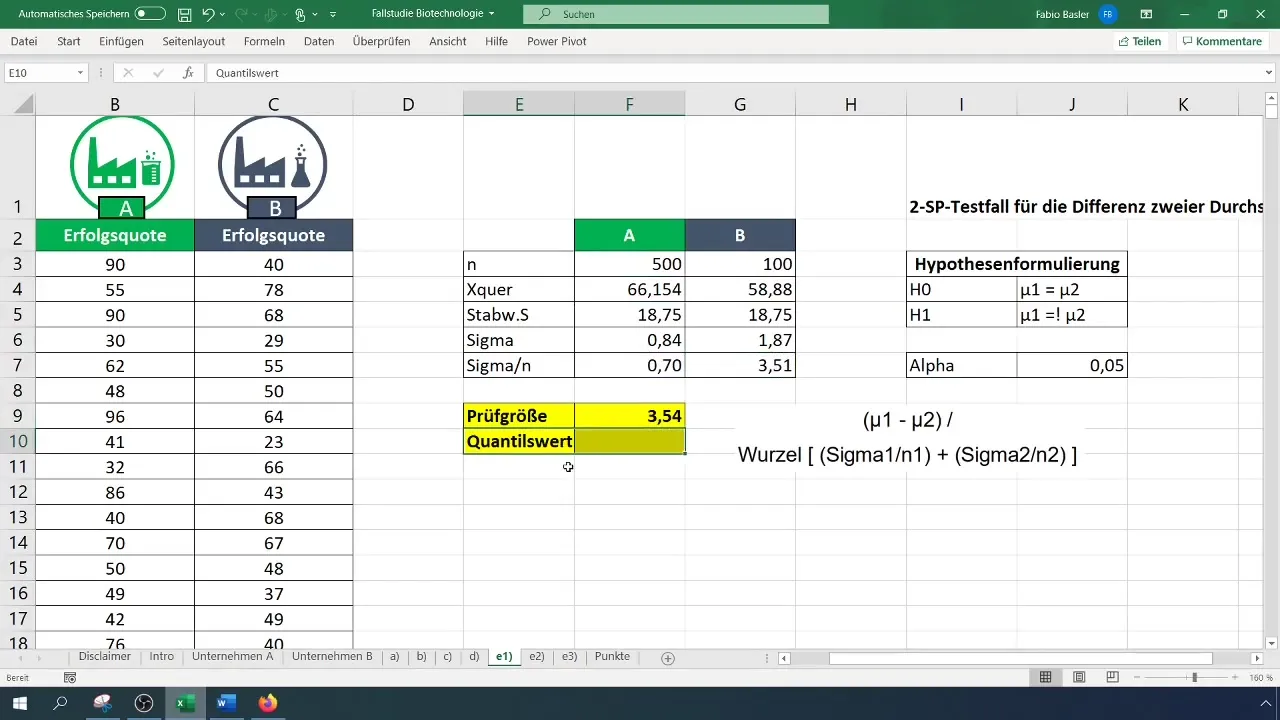
ステップ6:臨界値の決定
臨界値を見つけるために両側t分布を使用します。アルファ値を0.05に設定します。t分布表を確認するか、Excelで直接因子を計算してください。
ステップ7:仮説の決定
計算された検定統計量を臨界値と比較します。検定統計量が臨界値よりも大きい場合、帰無仮説(H_0)を棄却し、代替仮説(H_1)を確認します。
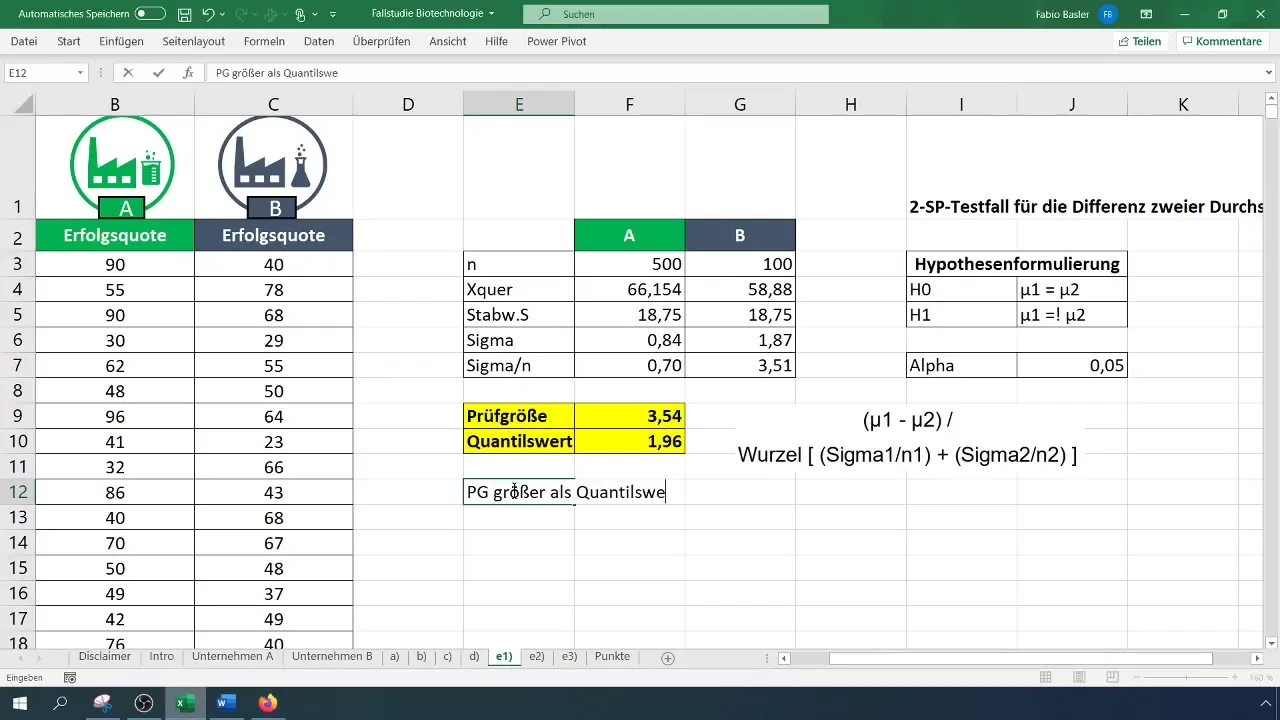
ステップ8:結果の解釈
最後に、結果を解釈します。この例では、両企業の平均成功率が有意に異なると結論付けられました。
要約
Excelで2標本t検定を実行して、2つのグループの平均値の違いを調査する手順を学びました。データ準備から仮説の立案、結果の解釈までのステップは、妥当で情報を提供するために重要です。
よくある質問
2標本t検定とは何ですか?2つのグループの平均値を比較し、それらが有意に異なるかどうかを確認する検定です。
どのようにして仮説を立てますか?帰無仮説(H_0)は平均値が等しいとし、対立仮説(H_1)は異なるとします。
検定統計量はどのように計算しますか?検定統計量は、平均値の差を各標本の分散の合計の平方根で割ることによって計算されます。
計算の後に何をしますか?検定統計量を臨界値と比較し、帰無仮説を棄却できるかどうかを判断します。
なぜ標準偏差が重要ですか?標準偏差はデータの変動性を理解するのに役立ち、検定統計量の計算に重要です。


