統計的テストは、特にグループ間の違いを調べる際に、データ分析の欠かせない要素です。研究やビジネスでよく使用される確立された手法の1つが、2標本F検定です。このガイドでは、Excelを使用して、2つの製薬会社の研究費に関する変数を比較するためのこのようなテストを実施する方法をステップバイステップで示します。
重要な知見
- 2つのグループの分散をF検定で比較する方法を学びます。
- このガイドには、Excelでテストを実行するための手順が詳細に記載されており、データ分析機能の使用方法も示されています。
- 結果の解釈方法とその結論について理解することができます。
ステップバイステップガイド
ステップ 1: データの準備
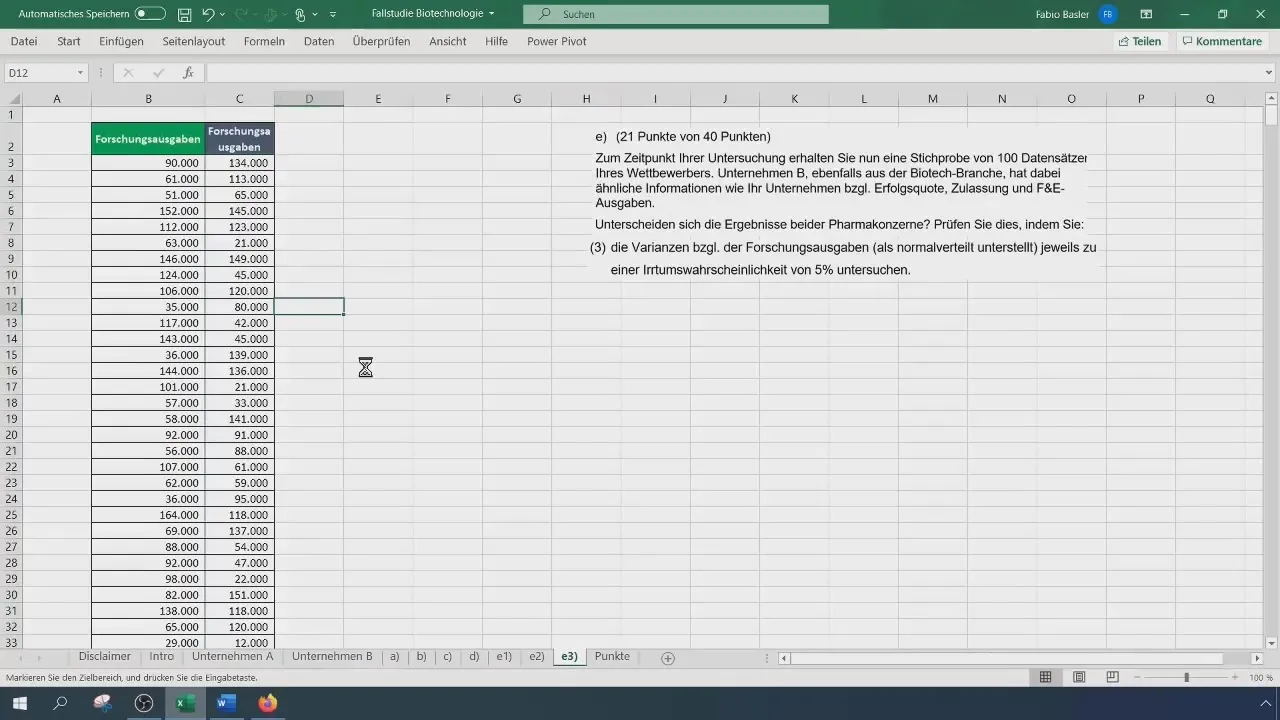
まず、両社の研究費の生データが必要です。Excelファイルを開き、それぞれの会社の研究データを別々の列にコピーします。

ステップ 2: 標本数と分散を計算する
企業Aは500、企業Bは100のサンプルサイズを維持します。データの分散を計算するには、VAR.S() 関数を使用してグループの分散を推定します。正確な結果を得るために、Excel形式で値を入力してください。
ステップ 3: 仮説を設定する
F検定のための仮説は次のように設定されます:
- 帰無仮説(H0):σ1² = σ2²(2社の分散は等しい)。
- 対立仮説(H1):σ1² ≠ σ2²(2社の分散は異なる)。
ステップ 4: 検定統計量を計算する
2つの分散の比を用いて検定統計量(F統計値)を計算します。計算には、Var_A / Var_B の式を使用します。適切に分散を入力すると、比較用のF統計値が得られます。
ステップ 5: 臨界値を決定する
臨界F値を計算するには、アルファレベル(通常は0.05)と自由度が必要です。自由度の計算方法は df1 = n1 - 1 および df2 = n2 - 1 です。F.INV() 関数を使用して臨界値を計算してください。

ステップ 6: 判断を下す
計算されたF統計量を臨界F値と比較してください。F統計量が臨界値よりも大きい場合、帰無仮説を棄却し、そうでない場合は棄却しません。この例では、棄却の基準は、検定統計量が基準値(臨界F値)よりも小さい必要があるということです。

ステップ 7: Excelデータ解析を利用する
Excelでは、データ分析機能を使用してF検定を実行することもできます。「データ」に移動し、「データ分析」を選択します。「2標本F検定」を選択し、2つの変数の範囲を入力して適切な設定を選択します。
ステップ 8: 結果の解釈
F検定の結果を分析してください。Excelの出力で計算されたF統計量とp値が手動計算と同じ結果を提供する場合、2つの企業の分散が等しいと結論づけることができます。
まとめ
2標本F検定は、2つのグループの分散の違いを比較するための統計分析における重要なツールであり、Excelでデータの準備から結果の解釈まで効果的にテストを実施する方法を紹介しました。
よくある質問
2標本F検定とは何ですか?2標本F検定は、2つのグループの分散を比較し、それらが統計的に有意に異なるかどうかを判断します。
F-検定はいつ使用すべきですか?F検定は、2つの独立したグループの分散の等質性を調べる場合に使用されます。
F統計量はどのように計算すればよいですか?F統計量は、第1グループの分散を第2グループの分散で割ることによって計算されます。
帰無仮説が棄却された場合はどうすればよいですか?帰無仮説が棄却された場合、2つのグループの分散は統計的に有意に異なると判断できます。
F検定の代替手法はありますか?はい、分散の均質性をテストしたい場合は、Bartlett検定やLevene検定を使用することができます。


