χ²適合度検定は、与えられたデータ列が正規分布に従うかどうかの仮説を検証するための簡単な方法を提供します。このガイドでは、スマートフォンの売上が正規分布に従っているかどうかを確認するために、Excelでχ²検定を実行する方法を学びます。これには、クラス化された頻度表の作成から検定統計量の計算とχ²臨界値との比較まで、段階的な手順が含まれます。
重要なポイント
- χ²適合度検定は、正規分布を検定する際に役立ちます。
- クラス化された頻度表を作成することが重要です。
- 検定統計量は臨界値と比較して、帰無仮説を採択または棄却します。
段階的な手順
ステップ1: データの準備
χ²検定を行うためには、まずデータが必要です。スマートフォンの売上データをExcelシートにコピーしてください。データが1つの列に整理されていることを確認してください。

ステップ2: ヒストグラムの作成
データの分布について視覚的な手がかりを得るために、データのヒストグラムを作成してください。これを行うには、「挿入」を選択し、"グラフ"を選択して、データの範囲を選択してからヒストグラムを追加します。
ステップ3: クラス化された頻度表の作成
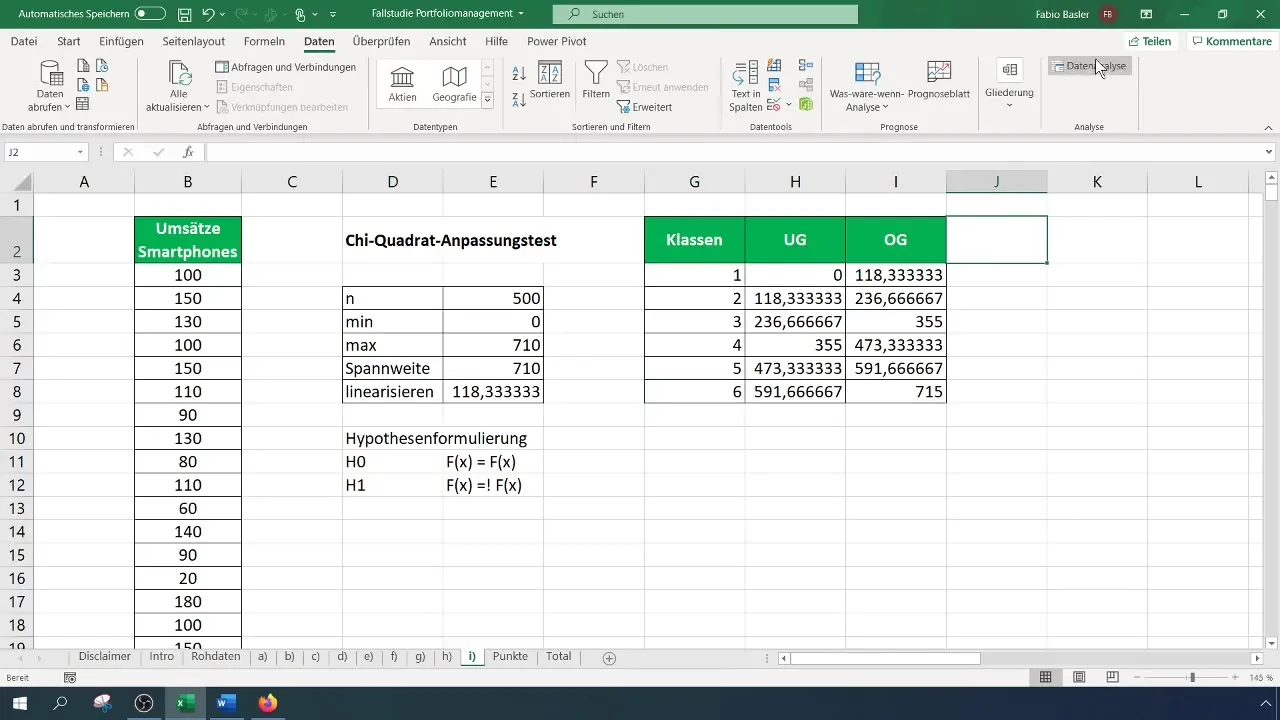
χ²検定には、クラス化された頻度表が必要です。まず、テーブル用のクラスの数を決定します - この場合、6つのクラスを使用します。階級の幅を計算し、それに応じてテーブルを作成してください。
ステップ4: 頻度の計算
各クラスの観測された頻度を計算する必要があります。メニューから "データ解析" を選択し、"ヒストグラム" を選択します。データの入力範囲とクラスの境界を選択し、頻度表の出力範囲を設定してください。
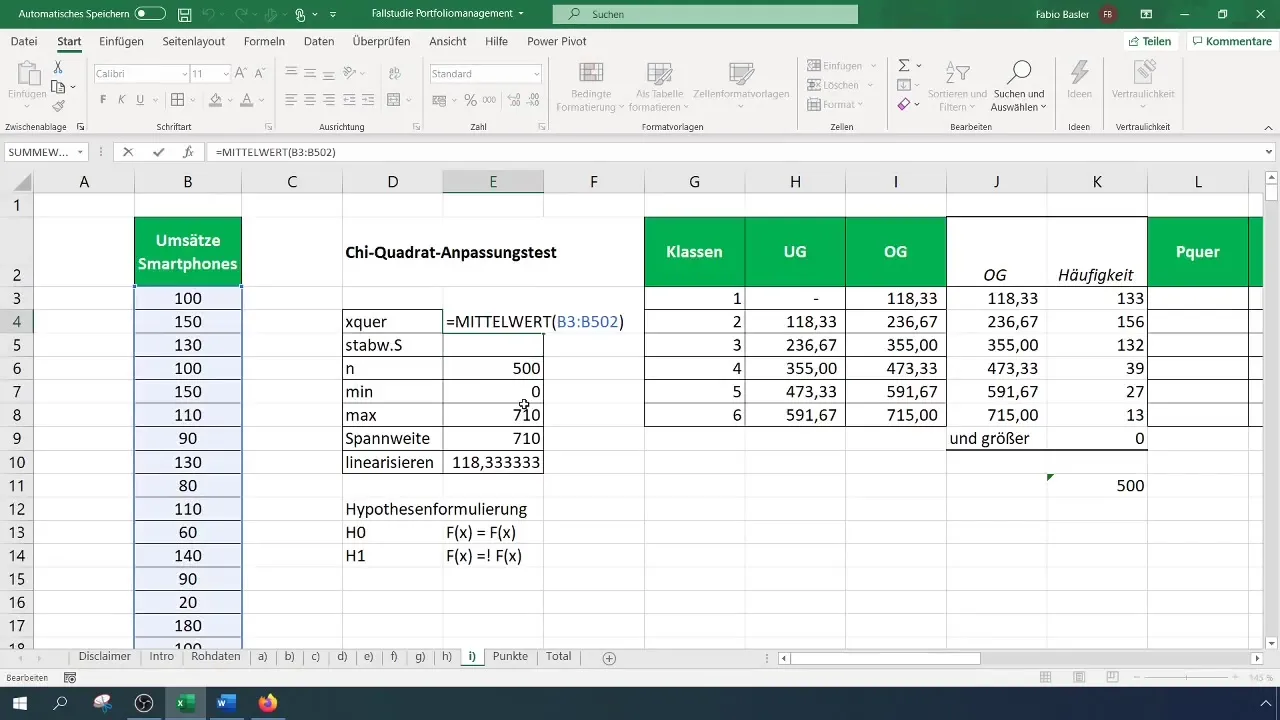
ステップ5: 期待される頻度の計算
期待される頻度を計算するために、仮定される正規分布に基づいて各クラスの確率を計算してください。このために、データの平均値と標準偏差が必要です。
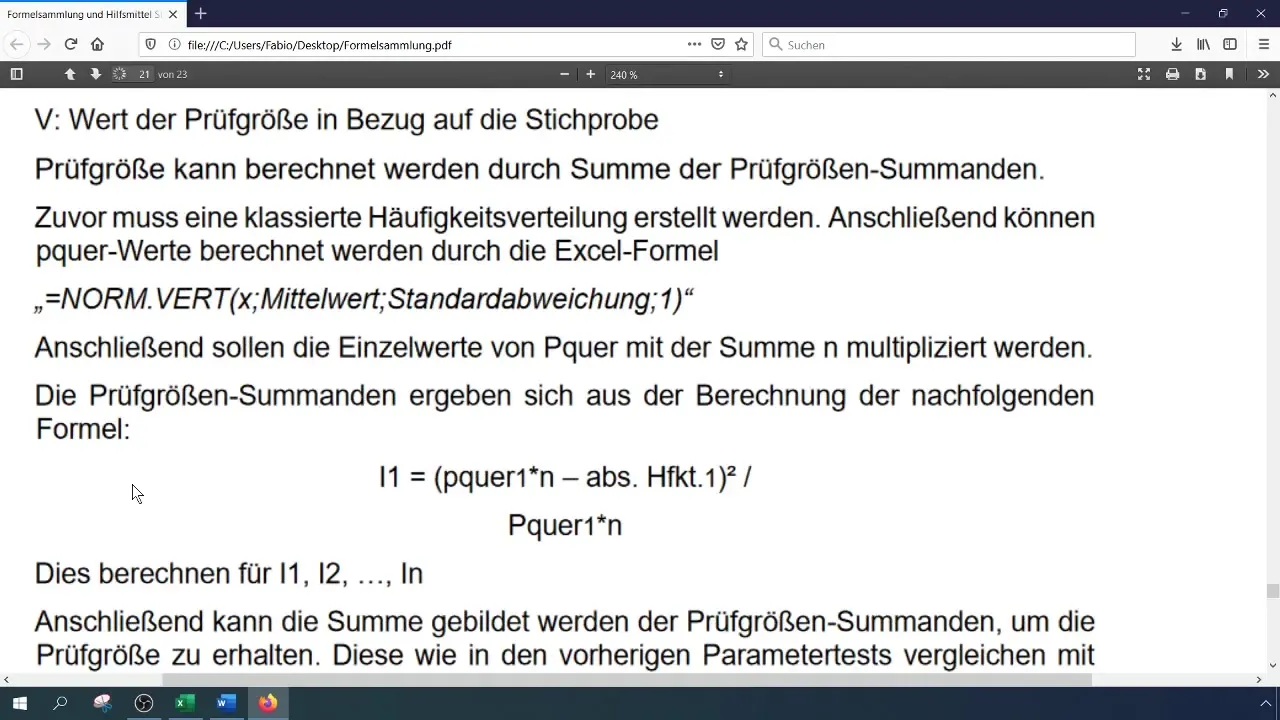
ステップ6: 検定統計量の計算
以下の式を使って検定統計量 (χ²) を計算してください:
[ \chi^2 = \sum \frac{(O_i - E_i)^2}{E_i} ]
ここで、(O_i) は観測された頻度、(E_i) は期待される頻度です。Excelでこれらの計算を行うには、個々のコンポーネントを別々のセルに保存します。
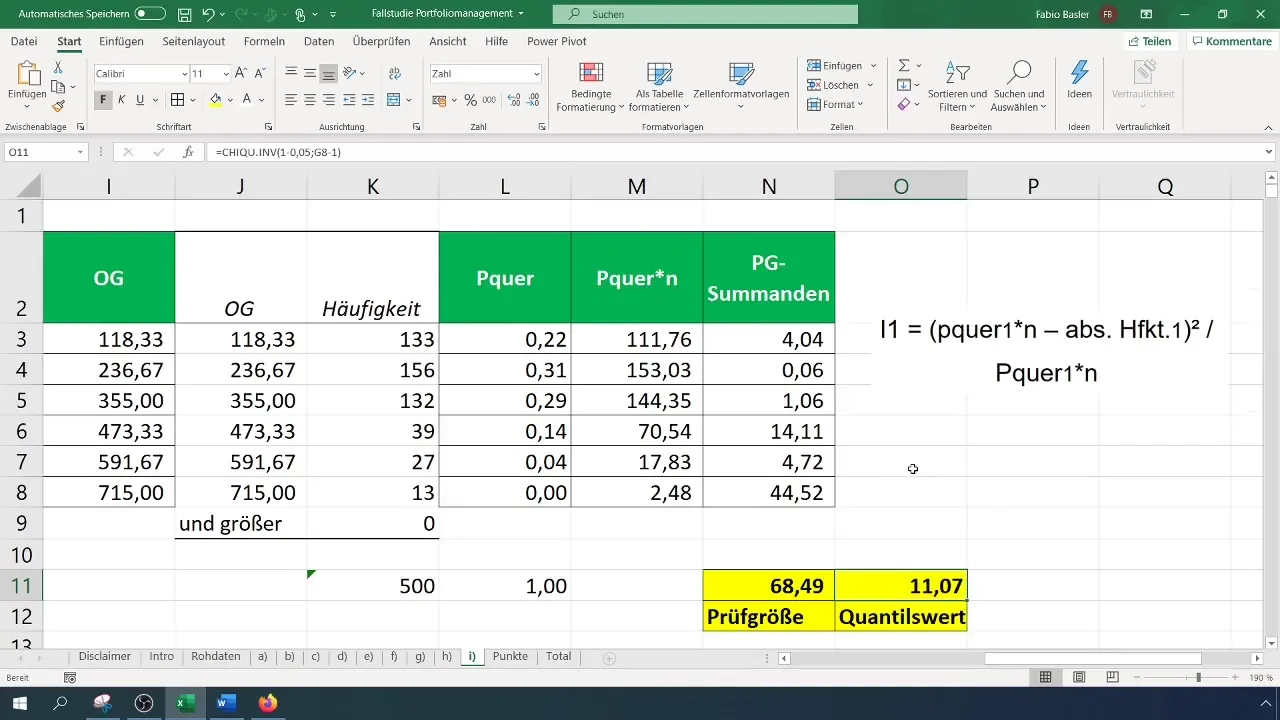
ステップ7: 臨界値の計算
検定統計量を評価するためには、信頼区間と自由度の数に基づいて臨界値 (χ²) を計算する必要があります。χ²検定の自由度の数は (k - 1) であり、ここで (k) はクラスの数である。
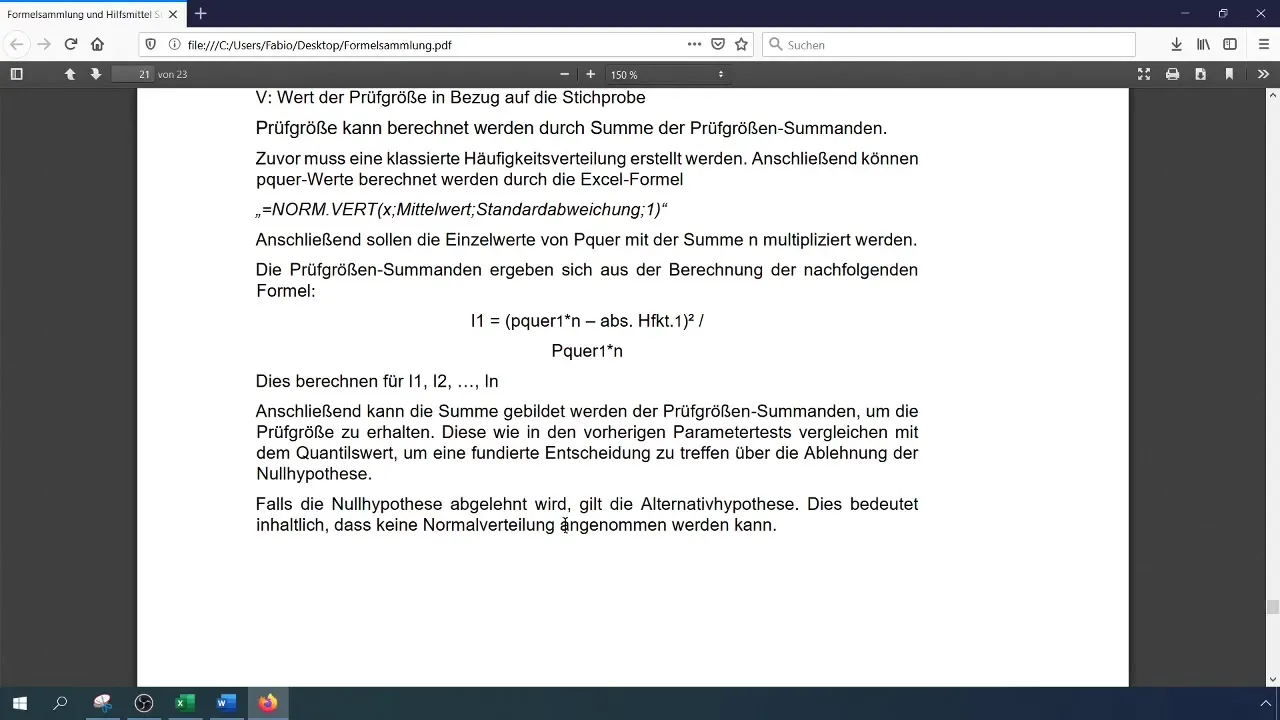
ステップ8: 仮説の検証
計算した検定統計量を臨界値と比較します。検定統計量が臨界値よりも大きい場合、データが正規分布に従っていないことを意味し、帰無仮説を棄却します。それ以外の場合は、帰無仮説を受容します。
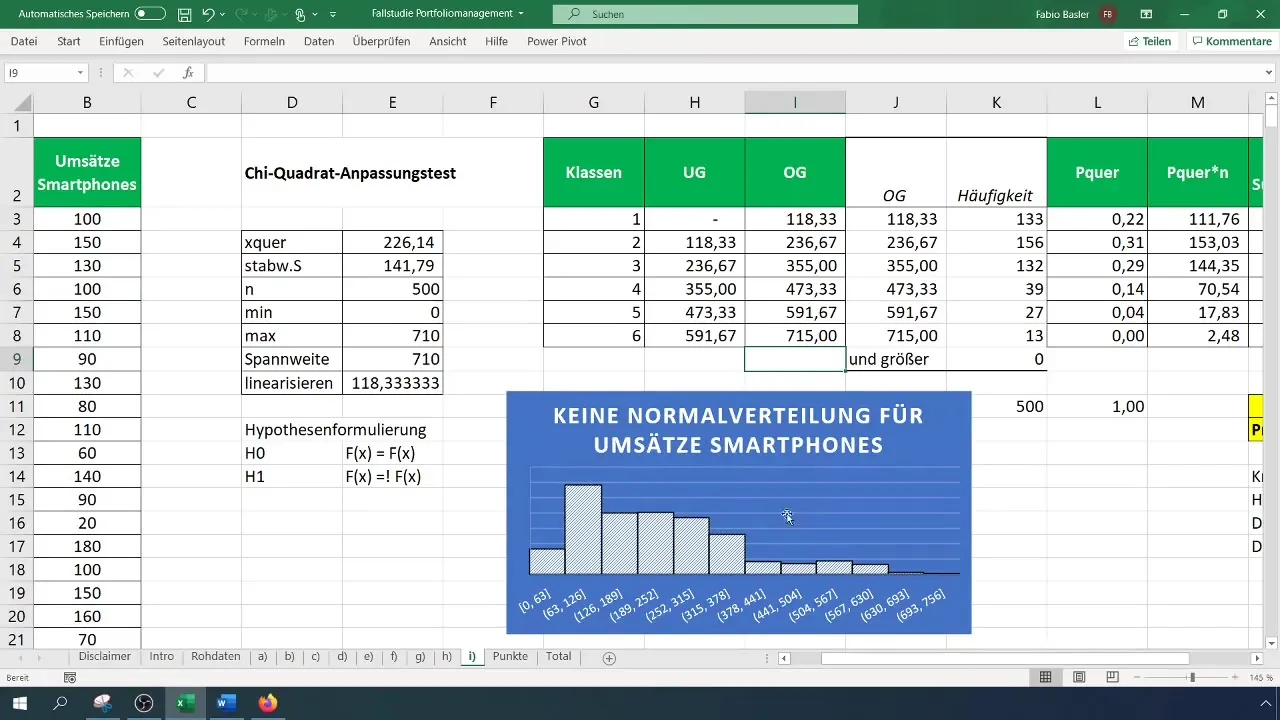
ステップ9: 結果の要約
あなたの結果を記録し、それにグラフィカルデータと仮説検定を追加してください。分布が正規でないことを視覚的に確認するためにヒストグラムを確認することを忘れないでください。
要約
本ガイドでは、スマートフォン売上の正規分布を分析するためにExcelでχ二乗適合度検定を行う方法を学びました。手順には、クラス付けされた頻度表の作成、期待される頻度、検定統計量の計算、そして最終的にはその値を臨界値と比較することが含まれます。
よくある質問
χ二乗適合度検定とは何ですか?χ二乗適合度検定は、観測された頻度分布が正規分布に一致するかどうかをチェックします。
頻度表には何クラスが必要ですか?データを実証的に分析するためには、通常、5〜10クラス以上が適切です。
帰無仮説が棄却された場合、どうしますか?帰無仮説が棄却されると、データが正規分布でないことを意味します。
臨界χ二乗値をどうやって計算しますか?臨界値は、自由度と希望する有意水準から、χ二乗分布表から読み取られます。


