統計的仮説検定はデータに基づいて意思決定をするための重要なツールです。このチュートリアルでは、Excelを使用して1標本検定を使用して、変数報酬システムを導入した後に企業の平均売上が向上したかどうかを判断する方法を学びます。この方法を適用することで、データに基づいた意思決定が可能になり、企業のパフォーマンスに貴重な洞察を得ることができます。
主な知見
- 仮説の立案と検証方法を学びます。
- Excelを使用して検定を行う際の統計式の活用方法を学びます。
- 結果の解釈により売上増加に関する根拠のある意思決定が可能となります。
ステップ・バイ・ステップ・ガイド
ステップ1: データの収集と準備
100週間にわたる平均売上データを含む無作為抽出標本にアクセスできます。これらのデータはあなたの検定の基礎となります。関連する情報をExcelワークシートに入力して作業を開始してください。

ステップ2: 仮説の設定
ヌル仮説(H0)と対立仮説(H1)を設定してください。あなたの場合、ヌル仮説は平均売上が41,000€以下であるか等しいことを示しています(m ≤ 41,000)。対立仮説は平均売上が41,000€よりも大きいことを示しています(m > 41,000)。
ステップ3: 平均値と標準偏差の計算
Excelの平均値関数を使用して標本から売上の平均値を計算してください。標準偏差を計算するには、帰無統計学で作業しているため、自由度を1減らす必要があるため、STABW.S式を使用してください。
ステップ4: 臨界値の決定
ExcelのNORM.S.INV関数を使用して臨界値を決定してください。引数に1 - α(0.98)を設定してください。テストの有意水準は2%です。

ステップ5: 検定統計量と臨界値の比較
計算された検定統計量を臨界z値と比較してください。検定統計量が臨界z値よりも大きい場合、ヌル仮説を棄却することができます。

ステップ6: 仮説に対する判断
検定統計量が臨界値を上回る場合、ヌル仮説を棄却し、平均売上が改善したと結論づけることができます。この判断を結果に記録してください。

ステップ7: 結果の解釈
結果の解釈は重要です。新しい平均値が46,669€であることを示し、前回の41,000€を上回っていることを示しています。これは、変数報酬システム導入後に売上が改善されたということを示し、従業員のモチベーションに肯定的な影響があることを示唆しています。
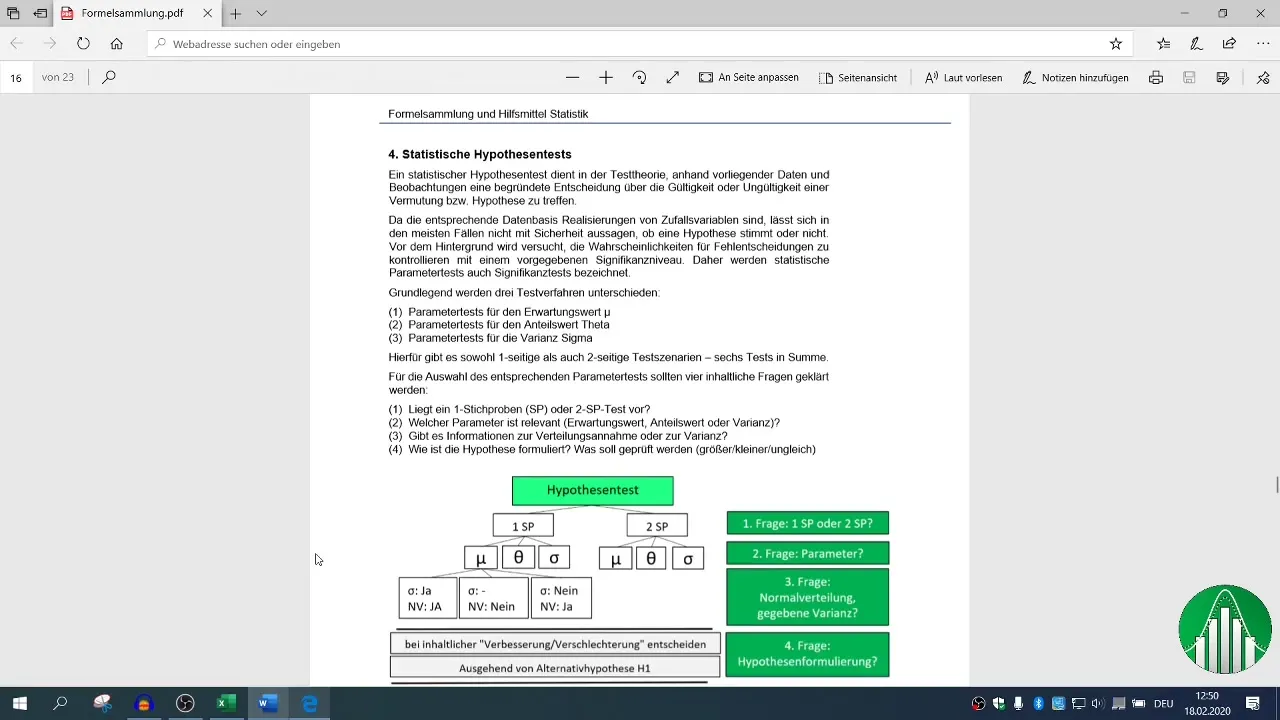
要約
このガイドでは、Excelで1標本検定を実行する方法を学びました。データ収集から仮説の設定、平均値と標準偏差の計算、仮説に対する判断まで、各ステップが正しい統計分析に不可欠でした。これらの知識を活用して、企業で根拠のある意思決定を行うことができます。
よくある質問
仮説をどのように立案しますか?ヌル仮説(H0)は現状を表し、対立仮説(H1)は変化を提唱します。
統計検定における検定統計量とは何を意味しますか?検定統計量は、ヌル仮説を棄却できるかどうかを判断するために使用されます。
検定統計量と臨界値の比較をどのように解釈すればよいですか?検定統計量が臨界値よりも大きい場合、ヌル仮説を棄却します。


