Excelで2標本F検定を実施

統計的仮説検定は企業が信頼性のある意思決定を行うための欠かせないツールです。次のセクションでは、Excelで二標本F検定を行い、売上データの分散に関する仮説の妥当性を検証する方法を紹介します。この手順書は、プロセスをステップバイステップで説明し、習得した技術を安全に適用するためのサポートを提供します。

主な知見

• 二標本F検定は、2つのデータグループの分散を比較するために使用されます。
• 目的は、現在の売上データの分散が仮定値から逸脱しているかどうかを検証することです。
• Excelには、必要な計算と比較を行うためのツールが提供されています。

ステップバイステップガイド

1. データ準備

テストを開始する前に、データが整えられていることを確認してください。すべての関連データを考慮するため、フィルターを削除することが重要です。適切な列にデータを選択する作業から始めてください。

2. パラメータの設定

テストのためのパラメータを定義してください。分析するデータポイントの数を把握しておく必要があります。例えば、今回の場合は、正規分布を持つ100の売上データポイントがあると仮定します。

3. 過去の分散値の取得

過去の知られている分散または売上値は、分析において中心的な役割を果たします。この例では、過去の値は週に116百万ユーロであるとします。

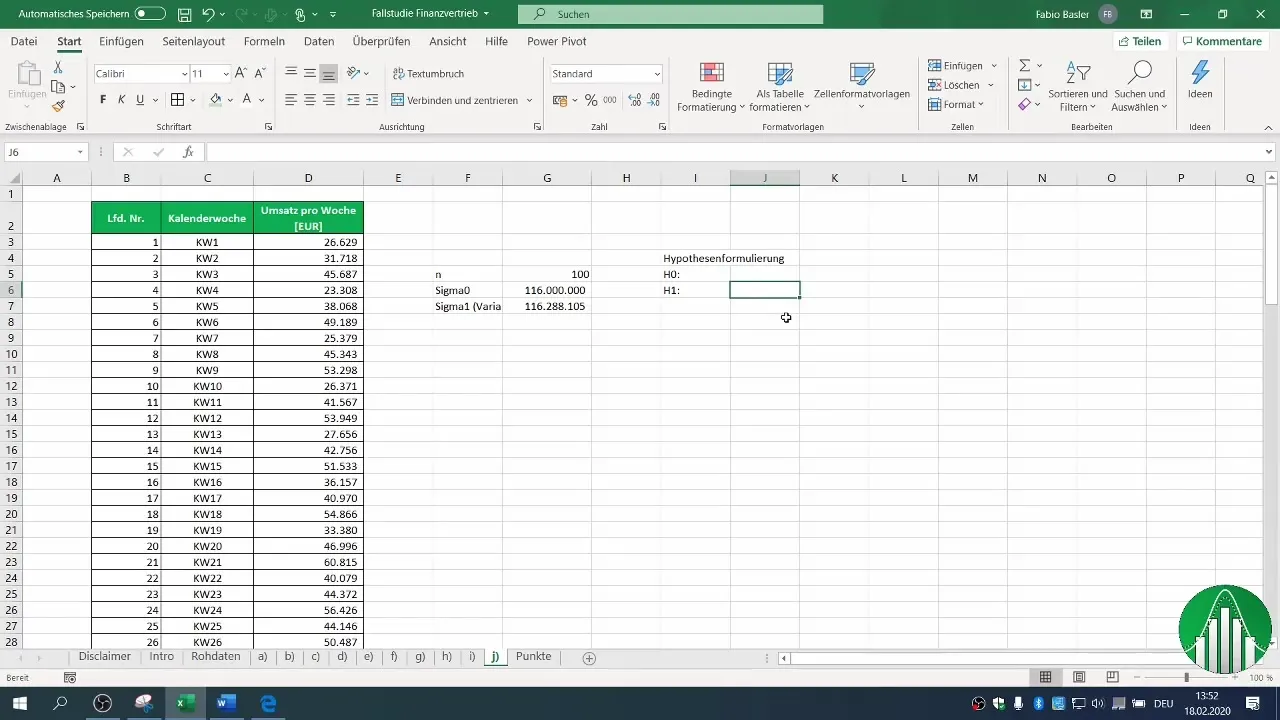
4. 仮説の設定

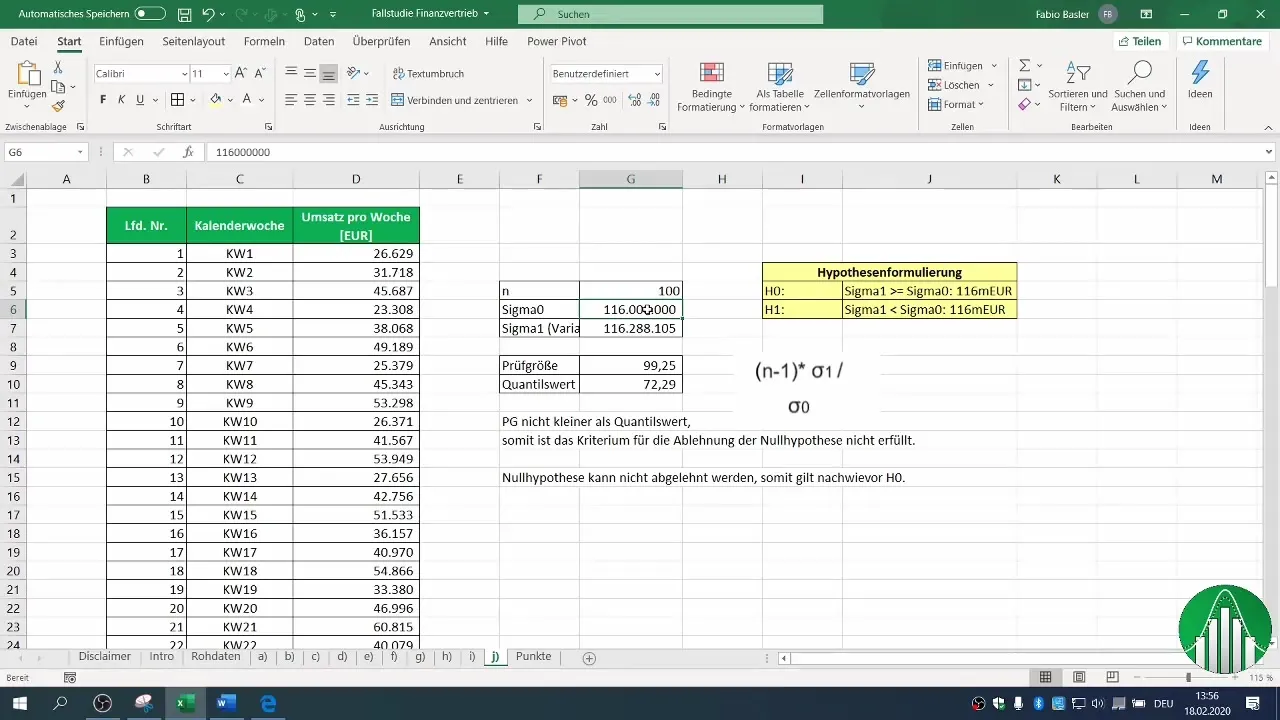
ヌル仮説（H0）と対立仮説（H1）を設定してください。この場合、H0は分散が116百万以上であると変わらないとし、H1は分散が減少したと仮定します。

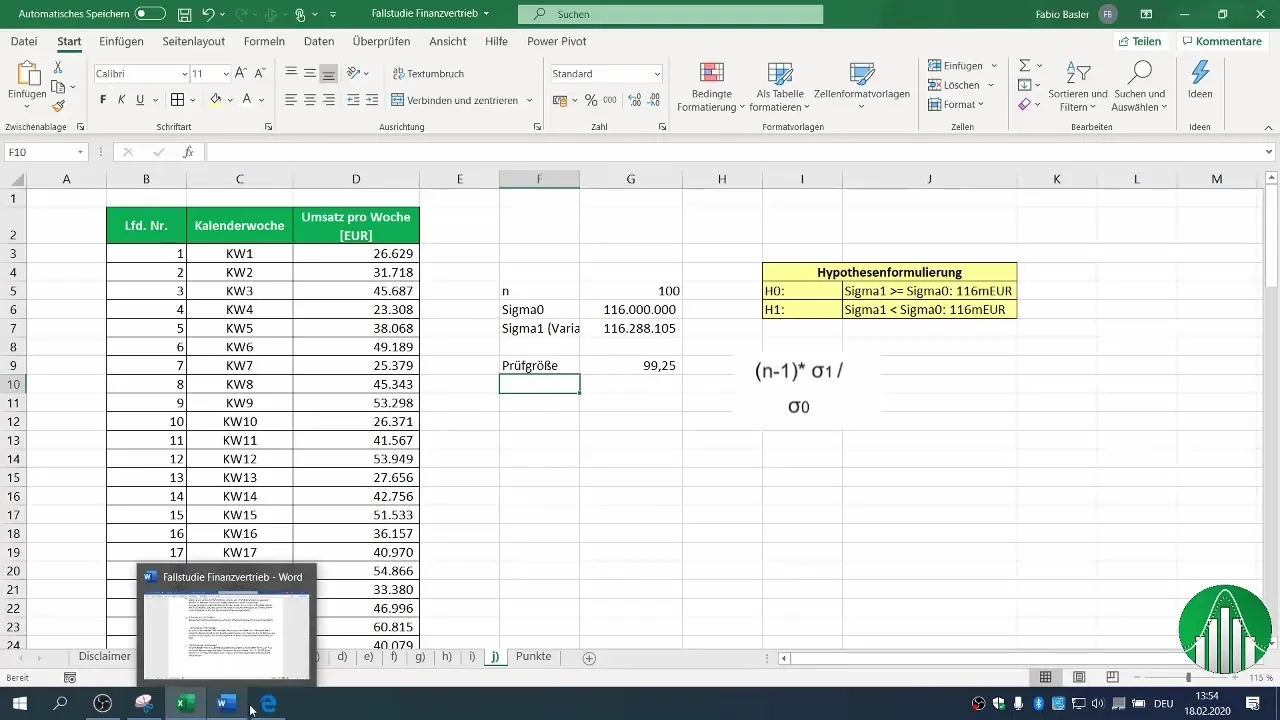
5. 検定統計量の計算

検定統計量は、サンプルの分散を使用して計算できます。必要な計算を行い、検定統計量の値を見つけます。これは以下の式で計算されます：（n-1） * σ1 / σ0、ここでσ1はサンプルの分散で、σ0は過去の分散を表します。

6. クリティカル領域の設定

ヌル仮説を棄却できるかどうかを決定するには、クリティカル領域を設定する必要があります。信頼区間に応じて、χ二乗分布表を使用してください。この例では、誤差確率を2％としました。

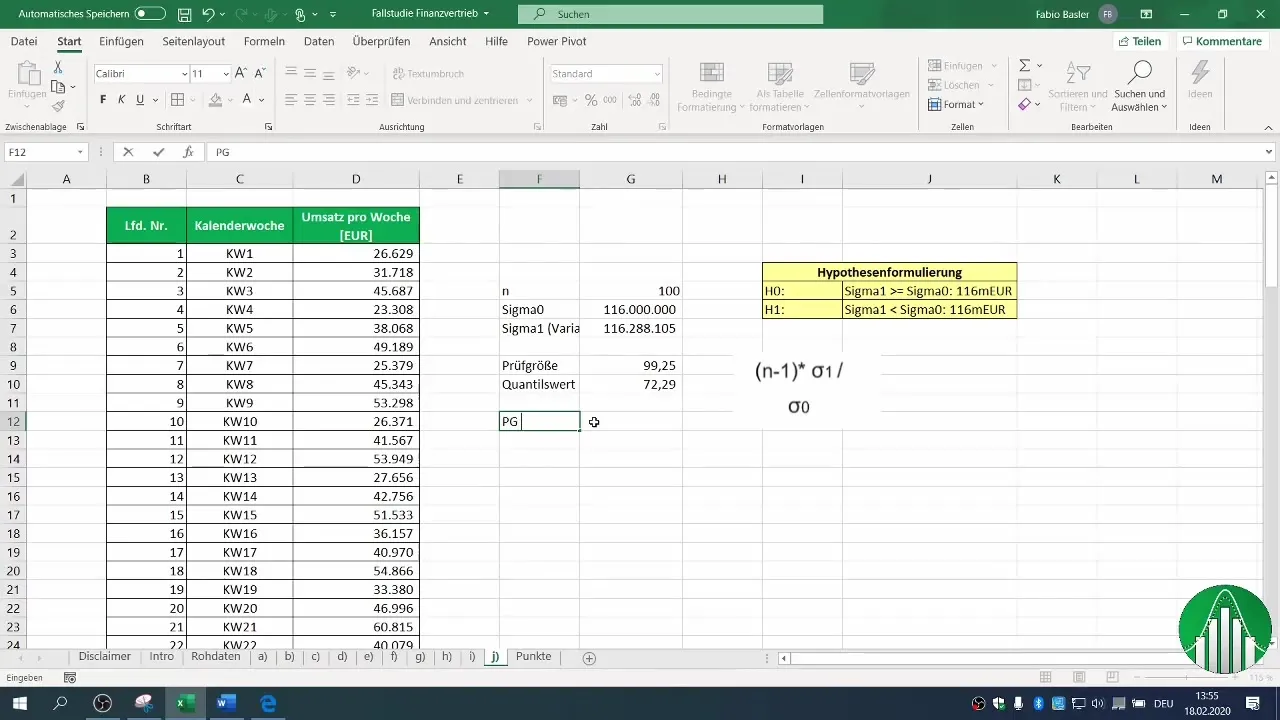
7. 検定統計量とクリティカル値の比較

今度は、計算された検定統計量がクリティカル値よりも小さいかどうかを確認してください。この場合、我々は検定統計量がクリティカル分位数よりも小さいことを発見しました。

8. 結論を導く

比較に基づき、ヌル仮説を棄却するかどうかを判断できます。この例では、我々はヌル仮説を棄却できないと結論づけました。これは、売上データの分散が引き続き仮定値に一致しているか、それ以上である可能性があることを示しています。

まとめ

この手順書では、Excelで二標本F検定を行う方法を詳しく学びました。データの準備、仮説の設定、検定統計量の計算、クリティカル領域の設定、最終的な結論を導く方法を理解しました。これらの手順により、統計的な分析を独力で行う準備が整いました。