Excel에서 양측 신뢰구간 계산

데이터 분석에 기초한 비즈니스 및 영업 환경에서 신중한 결정을 내리는 것이 중요합니다. 이중 측정 신뢰구간을 사용하여 어떤 매개변수의 실제 평균값이 일정 확률로 발생할 범위를 결정할 수 있습니다. 이 안내서에서는 엑셀을 사용하여 영업팀의 주간 매출에 대한 93 %의 신뢰 수준에서 신뢰 구간 한계를 계산하는 방법에 대해 안내해 드리겠습니다.

주요 인사이트

이중 측정 신뢰구간의 주요 측면은 다음과 같습니다:

1. 매개변수의 추정치로서 평균값의 계산.
2. 표본에서의 표준 편차 결정.
3. 구간의 하한 및 상한 결정을 위한 공식 적용.
4. 구간 위치를 결정하기 위한 신뢰 확률 적용.

단계별 안내

우선, 이 프로세스를 개괄하는 용어 및 단계에 대한 탄탄한 이해가 필요합니다.

단계 1: 데이터 준비

먼저 영업팀 A의 데이터를 준비해야 합니다. 관련 데이터를 필터링하고 엑셀 문서로 복사하세요.

단계 2: 평균값 계산

신뢰구간을 계산하려면 첫 번째 단계로, 예상 매출의 추정치로서 평균값을 결정해야 합니다. 엑셀에서는 =평균(범위) 공식을 사용하여 이를 수행할 수 있습니다. 여기서 "범위"는 영업팀 A의 주간 매출 데이터가 포함된 셀(들)을 의미합니다.

단계 3: 표준 편차 계산

표준 편차(σ)는 이중 측정 신뢰구간 계산에 중요합니다. 엑셀에서 =표준편차.S(범위) 공식을 사용하여 계산할 수 있습니다. 표본 표준 편차에 적합한 공식을 선택하는 것이 중요합니다.

단계 4: 표본 크기 결정

다음으로, 표본 크기를 결정해야 합니다. 영업팀 A에서 수집한 데이터 세트의 수를 더해주세요. 이 예시에서는 33개의 데이터 세트를 기준으로 하겠습니다.

단계 5: 평균값 표준 편차(σ_m) 계산

신뢰구간을 계산하려면 간단히 표준 편차를 표본 크기의 제곱근으로 나눈 평균값의 표준 편차를 계산해야 합니다.

단계 6: 분위수 결정

이중 측정 신뢰구간을 계산하려면 분위수가 필요합니다. 93 %의 신뢰 수준을 갖는다면 α는 7 %이고, 분위수의 분포는 엑셀 함수를 사용하여 찾을 수 있습니다.

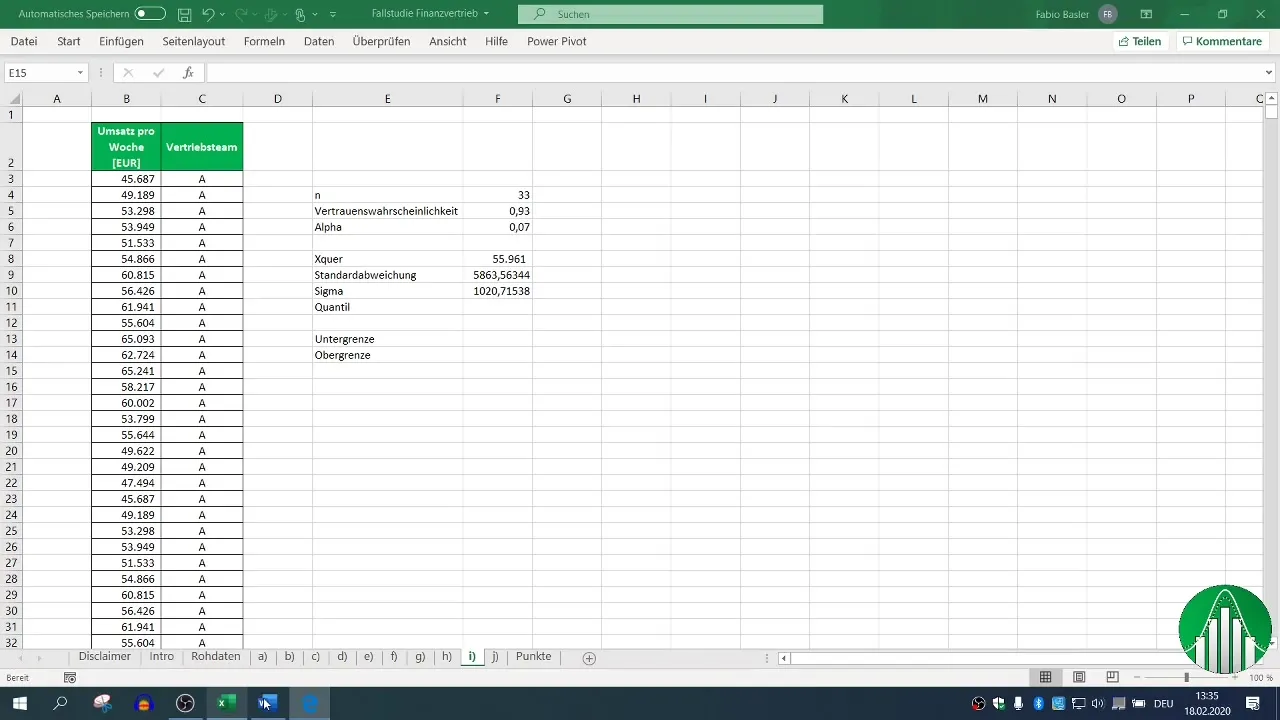
단계 7: 하한 값 계산

이제 표준편차의 곱과 분위수를 제외한 평균 값(x̄)에서 하한 값이 계산됩니다.

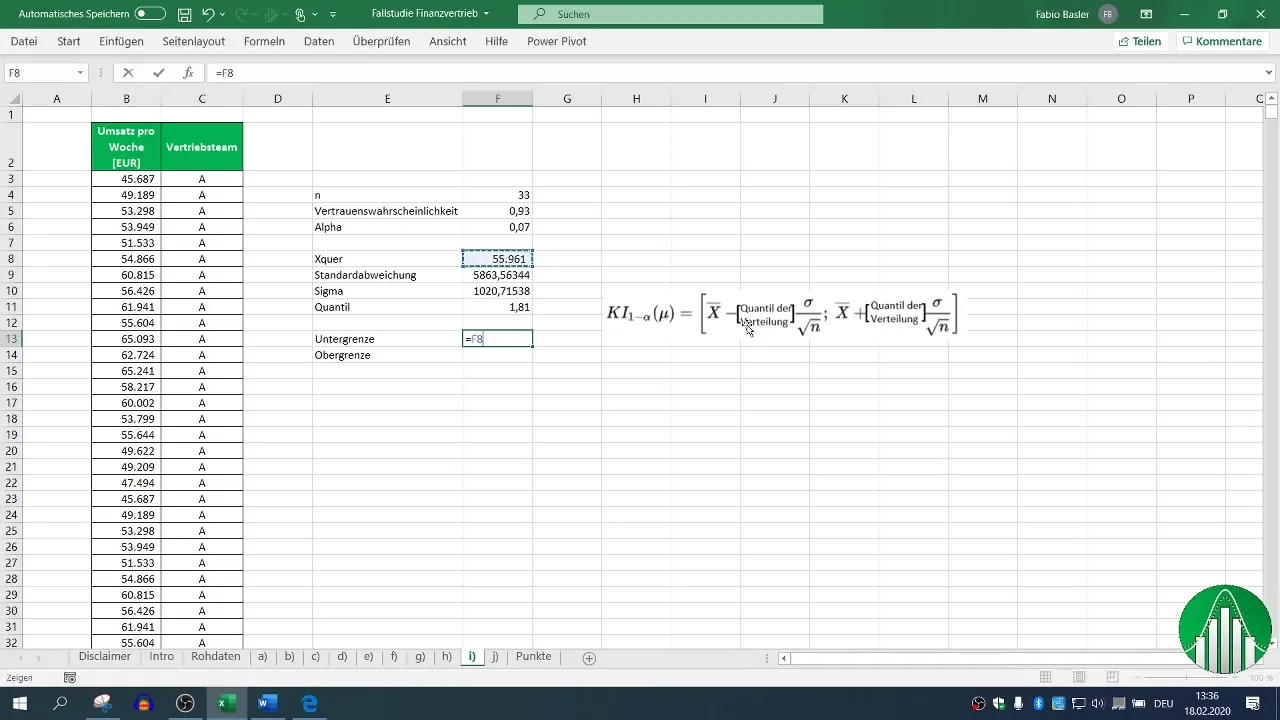
단계 8: 상한 값 계산

상한 값은 비슷하게 계산되지만 덧셈으로 대체됩니다.

단계 9: 결과 해석

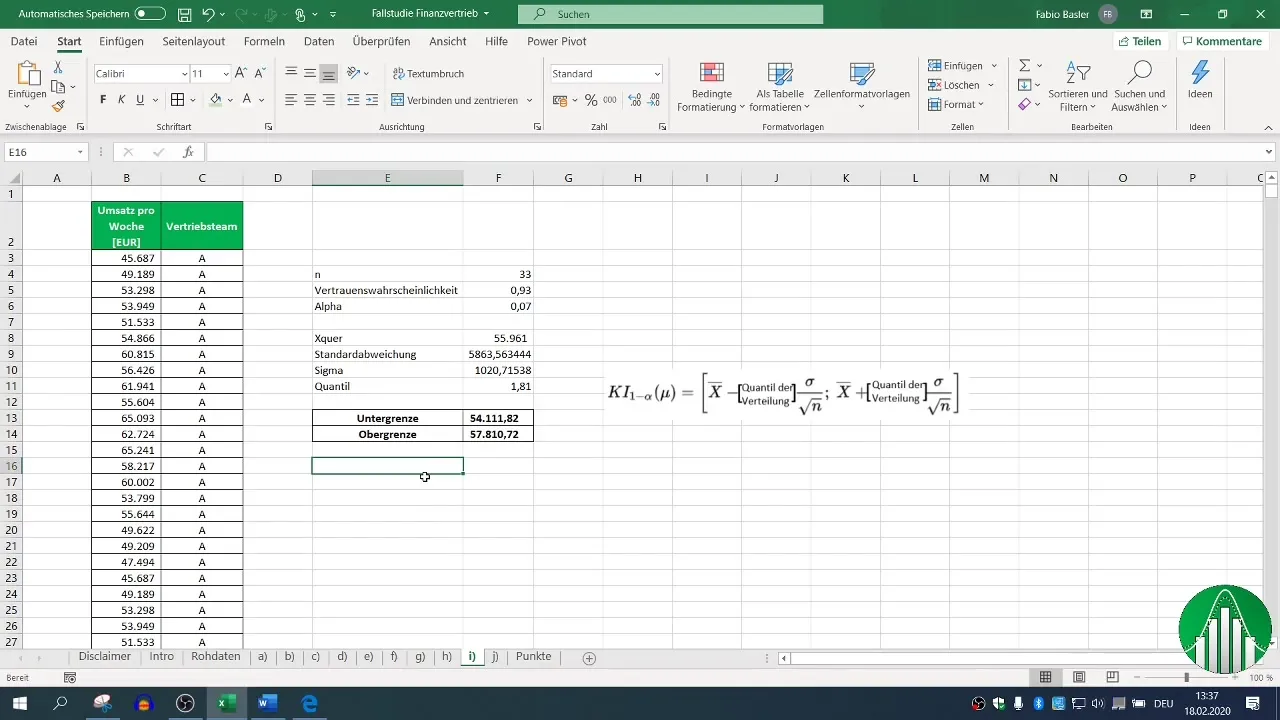
이러한 계산을 통해 영업팀 A의 주간 매출에 대한 이중 측정 신뢰구간을 얻게 됩니다. 이 예시에서는 54,111과 57,810 사이의 구간을 얻었습니다. 이는 93 %의 신뢰도로 이 범위에서 실제 평균 매출 값이 있음을 의미합니다.

요약

이중 측정 신뢰구간을 정확하게 계산함으로써 미래 매출에 대한 정확한 진술을 할 수 있습니다. 관련 데이터를 준비하고 평균과 표준 편차를 계산하며 최종적으로 구간을 결정하는 방법을 배웠습니다. 이 방법을 활용하여 영업 분야에서 데이터를 기반으로 한 결정을 내릴 수 있습니다.