Sėkmingas tikėtinos vertės 1-SP testas programoje "Excel

Statistiniai testai yra pagrindinė duomenų analizės ir sprendimų priėmimo sudedamoji dalis. Ypač biotechnologijų srityje gali būti labai svarbu patikrinti hipotezes apie veikliųjų medžiagų sėkmę. Šiame vadovėlyje sužinosite, kaip " Excel" programa efektyviai atlikti vienos imties testą (1-SP testą) tikėtinai vertei su žinoma dispersija.

Pagrindinės išvados

Šiame vadove išmoksite:

• 1-SP testo teorinį pagrindą.
• Testo atlikimo "Excel" programoje žingsniai.
• Rezultatų aiškinimo.

Duomenų parengimas

Norint atlikti 1-SP testą "Excel" programoje, pirmiausia reikia atitinkamų duomenų. Mūsų pavyzdyje darome prielaidą, kad analizuojate veikliųjų medžiagų sėkmės rodiklį. Yra žinoma, kad vidutinis sėkmės rodiklis būdavo 59 %, o standartinis nuokrypis - 19. Pirmiausia turėtumėte įvesti duomenis į "Excel" skaičiuoklę.

Įsitikinkite, kad duomenys suskirstyti stulpeliais, kad vėliau galėtumėte juos pasiekti. Aiški apžvalga padės jums lengviau suprasti atskirus veiksmus.

Testo apžvalga

1-SP testas naudojamas patikrinti, ar vidutinė sėkmės reikšmė reikšmingai skiriasi nuo nustatytos reikšmės. Šiuo atveju tikriname, ar 59 % sėkmės rodiklį ateityje galima gerokai padidinti.

Hipotezių formulavimas

Labai svarbu, kokias hipotezes suformuluosite testui:

• Nulinė hipotezė (H0): Tikroji tikėtina reikšmė yra lygi 59 (σ = 59 %).
• Alternatyvioji hipotezė (H1): Tikroji tikėtina reikšmė yra didesnė nei 59 %.

Formuluojant hipotezes daugiausia dėmesio reikėtų skirti tam, ką tiksliai reikia patikrinti ir kaip tai pasireiškia jūsų kontekste.

Svarbu aiškiai suvokti nulinės ir alternatyviosios hipotezės skirtumą, nes jos sudaro tolesnių skaičiavimų pagrindą.

Imties rinkimas

Mūsų tyrimui imame 500 veikliųjų medžiagų imtį. Svarbu atkreipti dėmesį, kad imtis būtų atrinkta reprezentatyvi ir tinkamu metodu turėtų garantuoti, kad jūsų rezultatus būtų galima realiai perkelti į visą populiaciją.

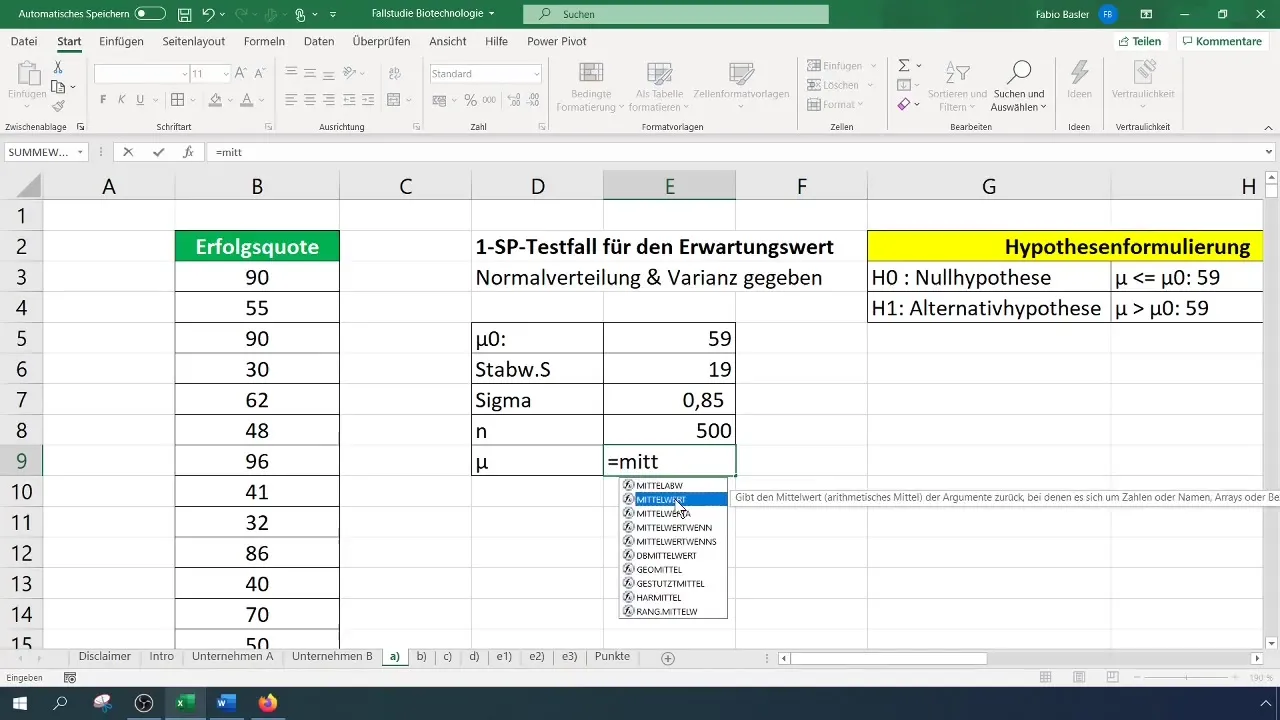
Atlikdami testą pirmiausia apskaičiuokite aritmetinį vidurkį. Tai turėtų būti nesunku padaryti naudojant atitinkamą "Excel" formulę.

Tyrimo kintamojo apskaičiavimas

1-SP testo kintamasis nustatomas pagal šią formulę

[ Z = \frac{\bar{x} - \mu_0}{\sigma/\sqrt{n}} ]

Čia (\bar{x}) reiškia jūsų imties vidutinę vertę, (\mu_0) - numanomą vidutinę vertę (šiuo atveju 59), (\sigma) - standartinį nuokrypį (šiuo atveju 19), o (n) - imčių skaičių (500).

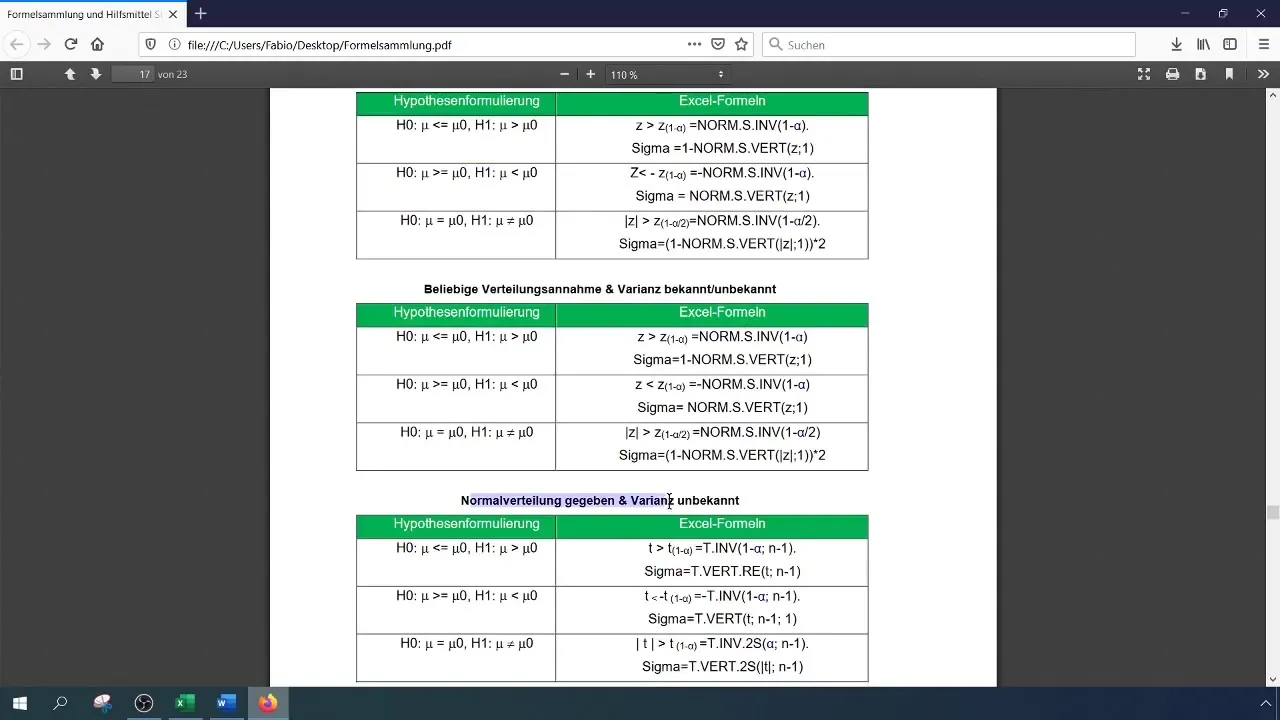
Į formulę įrašę reikšmes, apskaičiuokite testo statistiką, kad nustatytumėte, ar ji reikšminga, ar ne.

Kritinės reikšmės nustatymas

Esant 1 % (0,01) reikšmingumo lygiui, reikia perskaityti arba apskaičiuoti kritinę reikšmę. Tai galite padaryti "Excel" programoje naudodami funkciją NORM.S.INV.

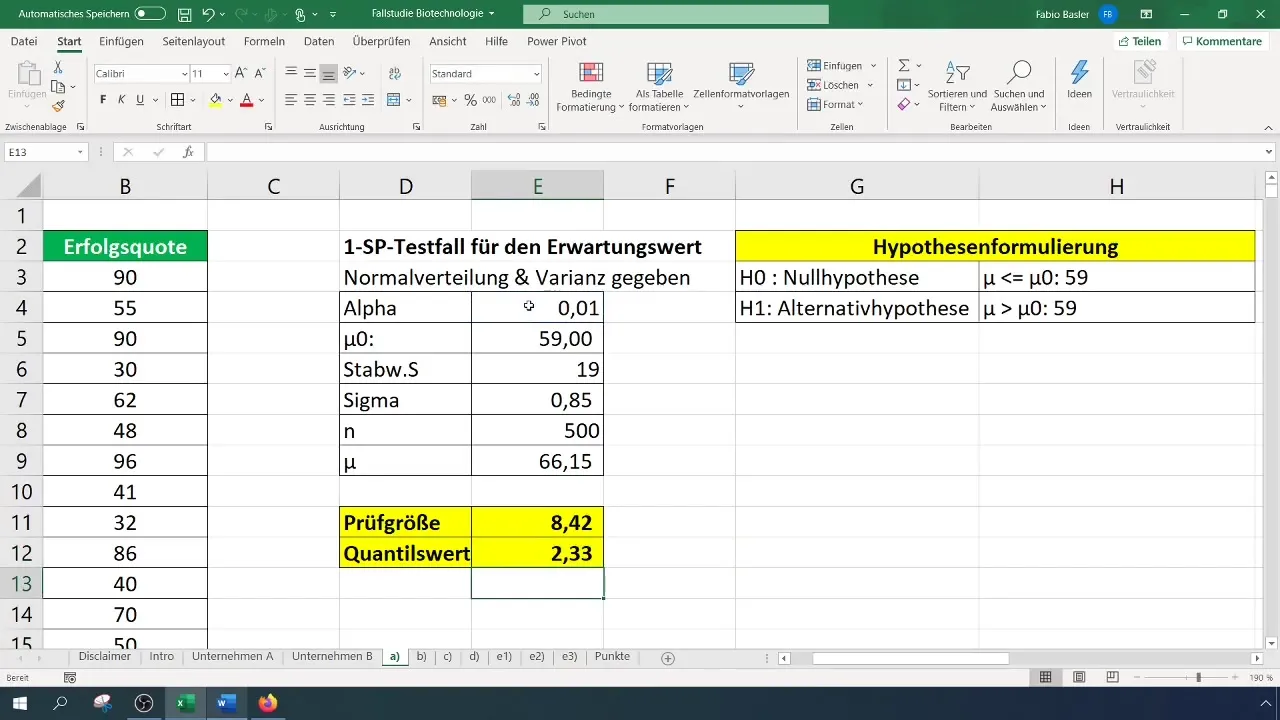
Formulė yra tokia:

[S.INV}(1 - \alfa) ]

Kur (\alfa) yra reikšmingumo lygmuo (0,01). Nustatyta reikšmė naudojama kaip palyginimo su tiriamuoju kintamuoju pagrindas.

Testo atlikimas

Dabar, kai jau turite ir testo statistiką, ir kritinę reikšmę, palyginkite jas abi:

• Jei testo statistika yra didesnė už kritinę reikšmę, nulinė hipotezė atmetama.
• Priešingu atveju nulinės hipotezės atmesti negalima.

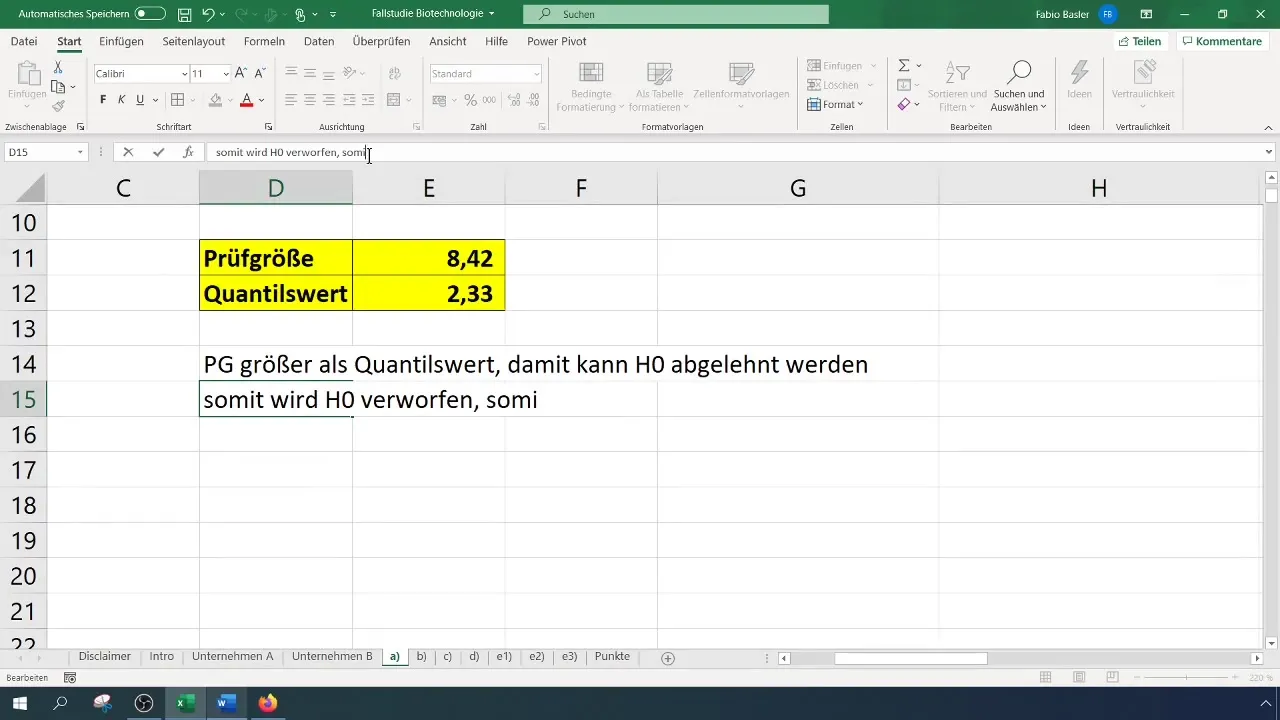
Mūsų atveju testo statistika yra 8,4, o tai viršija kritinę vertę 2,33. Todėl nulinę hipotezę galime atmesti. Tai rodo, kad sėkmės rodiklis reikšmingai pagerėjo.

Rezultatų aiškinimas

Atlikę testą ir gavę rezultatus, turėtumėte juos aiškiame kontekste interpretuoti. Nulinės hipotezės atmetimas reiškia, kad naujoji tiriamoji reikšmė reikšmingai skiriasi nuo ankstesnės, šiuo atveju 59 %.

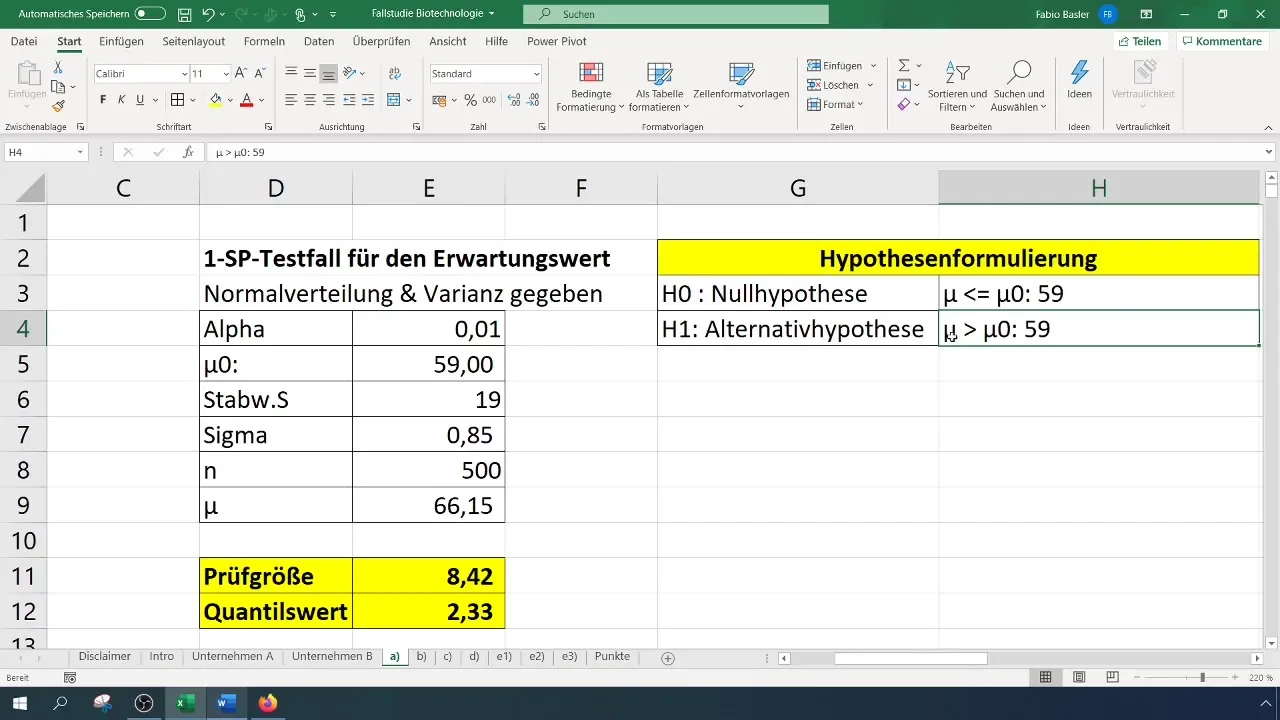
Ši informacija labai svarbi priimant strateginius sprendimus jūsų organizacijoje. Ji patvirtina, kad pastangos pagerinti sėkmės rodiklį buvo veiksmingos.

Apibendrinimas

Šiame vadovėlyje sužinojote, kaip "Excel" programa atlikti 1-SP tikėtinos reikšmės testą. Naudodamiesi atvejo analize, galėjote atlikti veiksmus nuo hipotezių nustatymo iki duomenų apskaičiavimo ir rezultatų interpretavimo. Šios žinios vertingos ne tik atliekant mokslinę analizę, bet ir praktiškai taikant įmonėje.