Statistinė analizė yra nepakeičiama portfelio valdymo priemonė. Regresinė analizė yra ypač galingas metodas, ypač kai reikia nustatyti kelių nepriklausomų kintamųjų įtaką priklausomam kintamajam. Ar norėtumėte sužinoti, kaip " Excel" programoje nustatyti ir analizuoti tiesinį funkcinį ryšį naudojant daugialypę regresiją? Šiame vadove rasite aiškią apžvalgą ir išsamias žingsnis po žingsnio instrukcijas.
Pagrindinės išvados
- Regresinė analizė padeda kiekybiškai įvertinti nepriklausomų kintamųjų įtaką priklausomam kintamajam.
- Svarbu įvertinti regresijos modelio kokybę ir statistinį reikšmingumą.
- Įvertinus koeficientus, galima nustatyti, kuris nepriklausomas kintamasis turi didesnę įtaką priklausomam kintamajam.
Žingsnis po žingsnio regresinės analizės vadovas "Excel" programoje
Duomenų parengimas
Prieš pradėdami regresinę analizę, turite paruošti duomenis. Šiuo atveju priklausomas kintamasis (y) yra nešiojamųjų kompiuterių apyvarta, o nepriklausomi kintamieji (x1 ir x2) yra darbuotojų skaičius ir konkurentų veiksmų skaičius. Pirmiausia visus reikiamus duomenis turėtumėte įvesti į "Excel" programą ir aiškiai juos susisteminti.
Patikrinkite koreliaciją
Galite sukurti koreliacijos matricą, kad gautumėte pradinius galimų kintamųjų sąsajų požymius. Ši matrica padeda pamatyti, kaip stipriai susiję skirtingi kintamieji. Tai galite padaryti naudodami "Excel" funkciją "Duomenų analizė" ir pasirinkę koreliacijos matricą, į kurią turėtumėte įtraukti visas svarbias duomenų sritis.
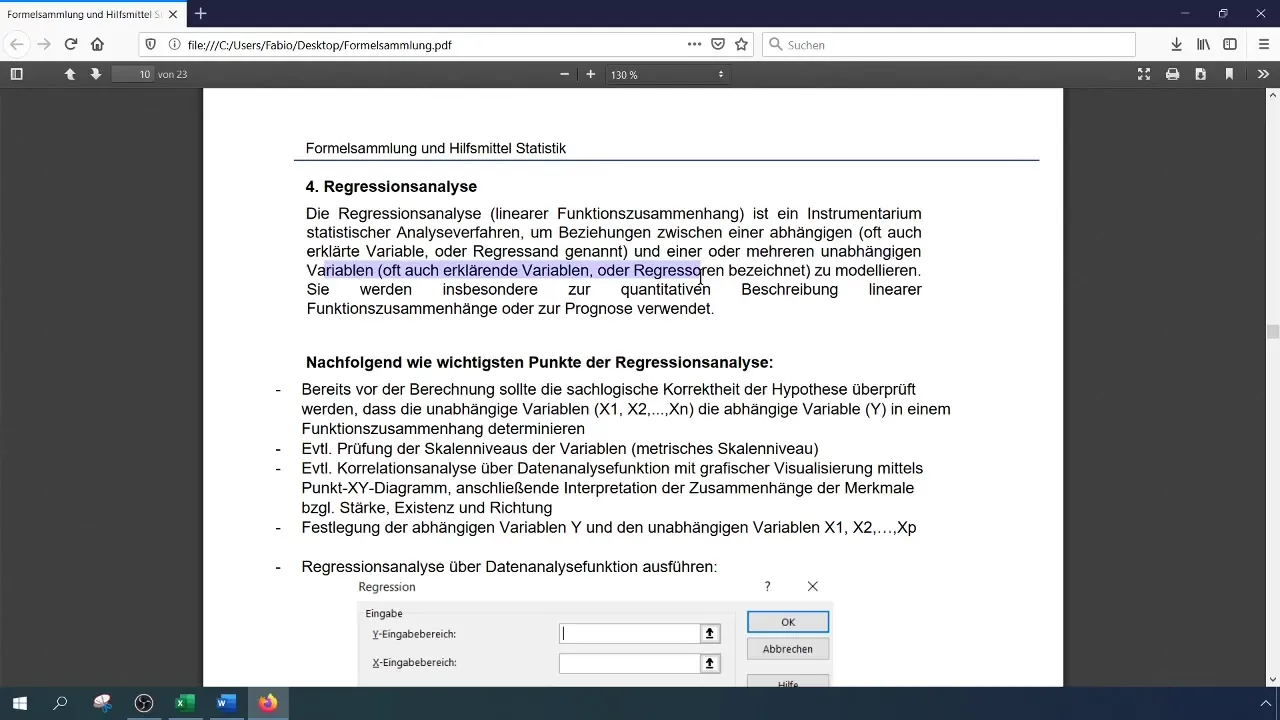
Regresinės analizės atlikimas
Dabar esate pasirengę atlikti regresinę analizę. Norėdami tai padaryti, dar kartą pasirinkite funkciją "Duomenų analizė", tada pasirinkite "Regresija". Čia įveskite priklausomo kintamojo (sąsiuvinių apyvartos) ir nepriklausomų kintamųjų (darbuotojų skaičiaus ir konkurentų veiksmų) įvesties sritį.
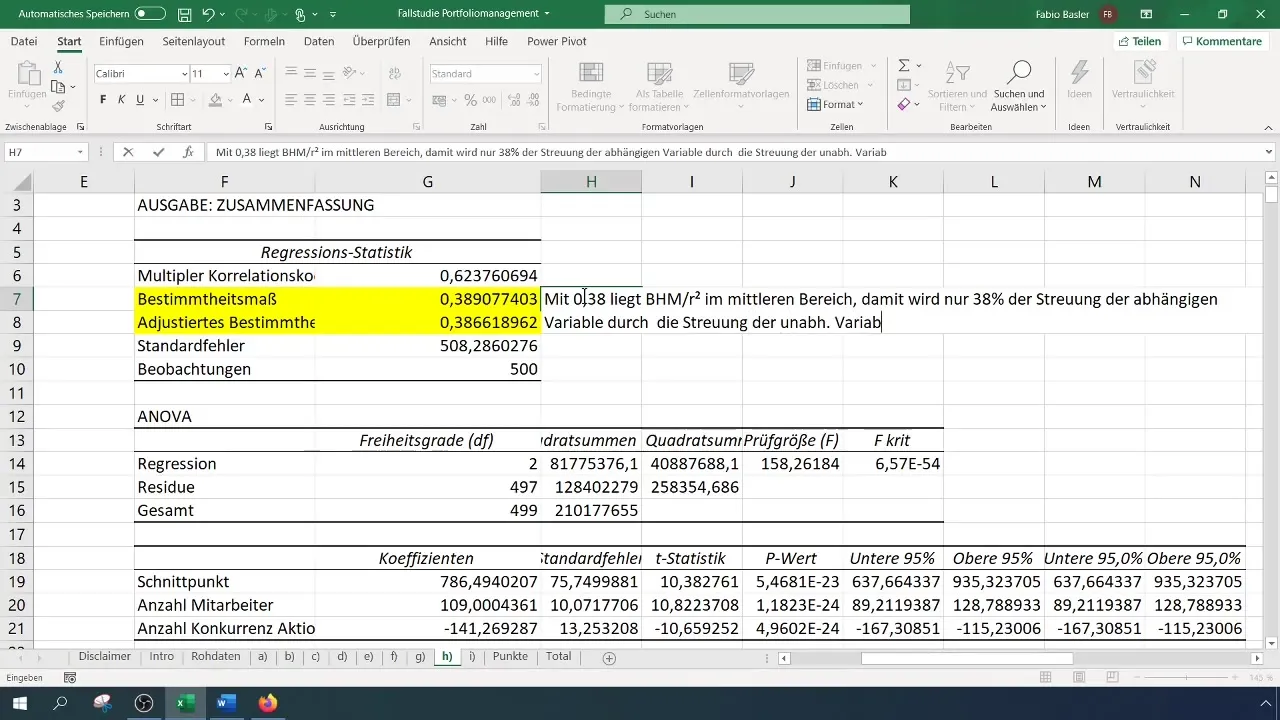
Rezultatų aiškinimas
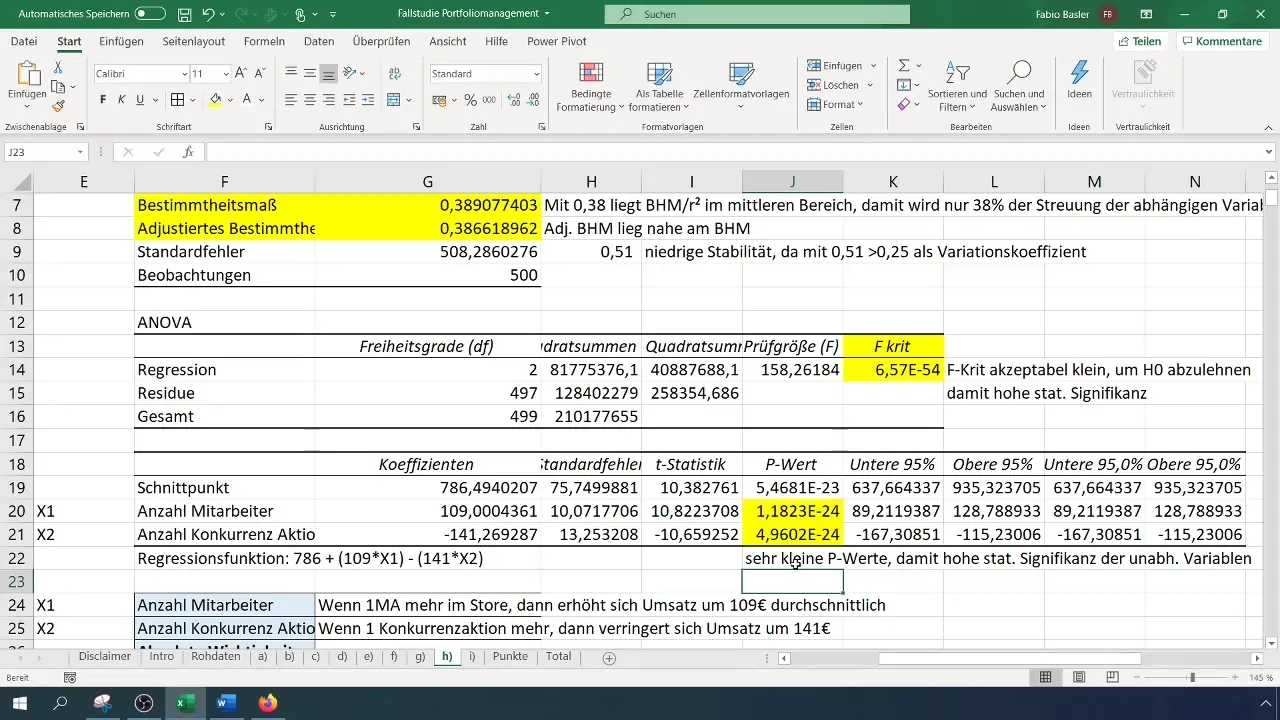
Atlikę regresinę analizę, gausite įvairių rezultatų ir statistinių duomenų. Pirmasis svarbus dalykas yra determinacijos koeficientas (R²), apibūdinantis priklausomo kintamojo paaiškinimo nepriklausomais kintamaisiais dalį. R² reikšmė 0,38 rodo, kad 38 % apyvartos kintamumo galima paaiškinti dviem nepriklausomais kintamaisiais.
Atliekant analizę reikėtų atkreipti dėmesį į tai, kiek stabilus yra modelis. Stabilumui nustatyti galite naudoti standartinę paklaidą. Pavyzdžiui, jei gaunate 0,51 standartinę paklaidą, tai reiškia didelį santykinį svyravimą, taigi ir mažą stabilumą.
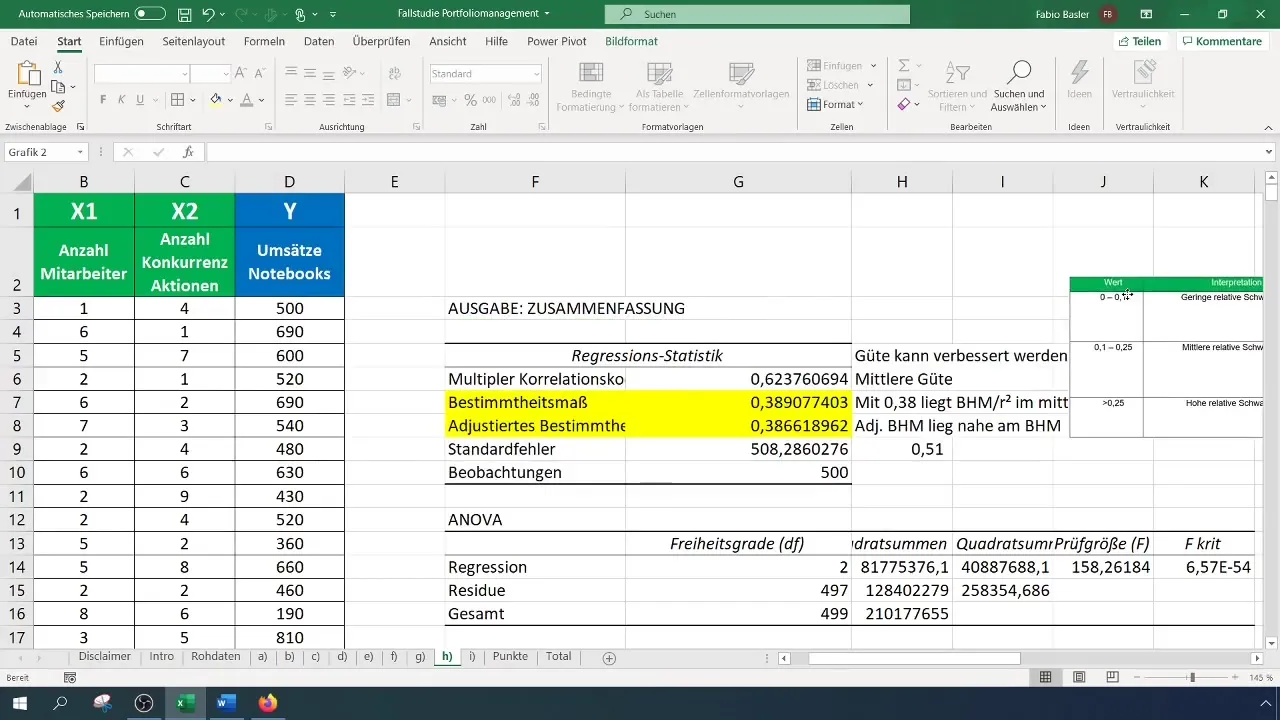
Stiprių įtaką darančių veiksnių vertinimas
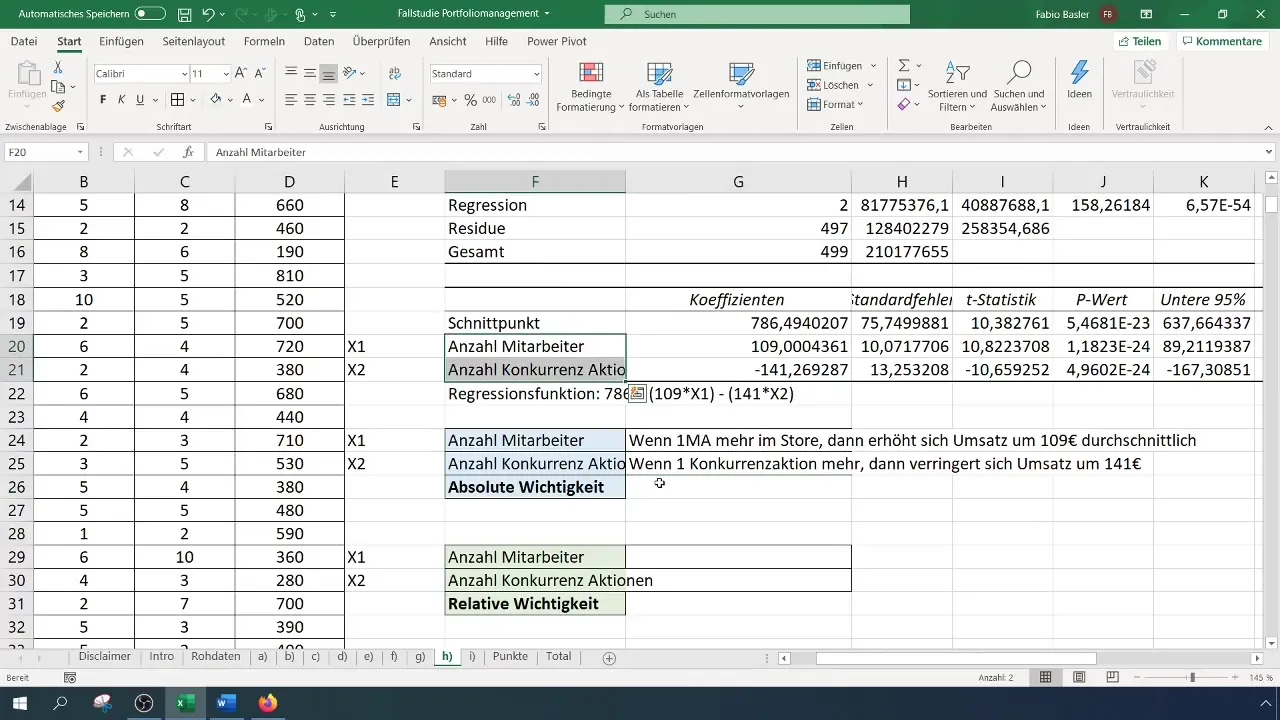
Labai svarbus žingsnis - išsiaiškinti, kuris iš nepriklausomų kintamųjų turi didesnę įtaką priklausomam kintamajam. Tai galite padaryti naudodami koeficientus, kurie rodo absoliučią kintamųjų svarbą. Šiuo atveju x1 (darbuotojų skaičius) koeficientas yra 109, o x2 (konkurentų veiksmų skaičius) koeficientas yra -141. Tai rodo, kad kiekvienas darbuotojų skaičiaus padidėjimas padidina pardavimus 109 eurais, o kiekvienas konkurentų akcijų skaičiaus padidėjimas sumažina pardavimus 141 euru.
Statistinio reikšmingumo vertinimas
Kitas svarbus regresinės analizės aspektas yra statistinis reikšmingumas. Tai galite pamatyti iš p-vertės ir F testo, kurių abi vertės turėtų būti labai mažos. Tai rodo, kad nepriklausomi kintamieji daro reikšmingą įtaką priklausomam kintamajam, ir tai pagrindžia modelio naudojimą.
Apibendrinimas
Regresinė analizė "Excel" programa leidžia kiekybiškai įvertinti skirtingų kintamųjų ryšį. Šiose instrukcijose susipažinote su daugialypės regresijos atlikimo ir interpretavimo etapais. Būtinai kritiškai įvertinkite modelio kokybę ir stabilumą, taip pat atskirus įtakojančius veiksnius, kad galėtumėte priimti pagrįstus portfelio valdymo sprendimus.
Dažniausiai užduodami klausimai
Kokių duomenų reikia regresinei analizei atlikti? Jums reikia priklausomo kintamojo (pvz., apyvartos) ir bent vieno ar daugiau nepriklausomų kintamųjų (pvz., darbuotojų skaičiaus, konkurencinių veiksmų).
Kaip aiškinti determinacijos koeficientą R²? Didesnė R² reikšmė reiškia, kad didesnę priklausomo kintamojo kintamumo dalį paaiškina nepriklausomi kintamieji.
Kaip galiu patikrinti statistinį reikšmingumą? Galite naudoti p reikšmes ir F testą; mažos reikšmės rodo didelį reikšmingumą.
Kuo skiriasi R² ir pakoreguotas R²? Pakoreguotame R² atsižvelgiama į nepriklausomų kintamųjų skaičių ir pateikiamas realesnis įvertis modeliams su keliais kintamaisiais.
Kaip galima įvertinti įtaką darančių veiksnių stiprumą? Tai atliekama nagrinėjant nepriklausomų kintamųjų koeficientus, kuriais kiekybiškai įvertinama kiekvieno kintamojo įtaka priklausomam kintamajam.


