Gebėjimas naudotis "Excel" duomenų analizės įrankiais yra labai svarbus norint sėkmingai dirbti versle ir pardavimuose. Šiame vadove daugiausia dėmesio skiriama koreliacinei ir regresinei analizei , siekiant išsiaiškinti, kaip darbuotojų skaičius ir telefono skambučių skaičius veikia pardavimų rodiklius. Abiejų analizių atlikimas padės kiekybiškai įvertinti šiuos ryšius ir leis suprantamai interpretuoti rezultatus.
Pagrindinės išvados
- Koreliacijos ir regresijos skirtumai: Koreliacija parodo dviejų kintamųjų ryšį, o regresija analizuoja kelių nepriklausomų kintamųjų poveikį priklausomam kintamajam.
- Įžvalgos apie modelio statistinį reikšmingumą ir kokybę.
- Kiekybinis regresorių svarbos įvertinimas.
Žingsnis po žingsnio vadovas
1. Pasirengimas duomenų analizei
Prieš pradėdami analizę, turite įsitikinti, kad duomenys "Excel" programoje yra tinkamai paruošti. Importuokite duomenis apie pardavimus, darbuotojų skaičių ir telefono skambučius į "Excel" darbalapį. Patikrinkite, ar visi duomenų rinkiniai yra išsamūs ir ar yra reikalingi kintamieji.

2 Atlikite koreliacijos analizę
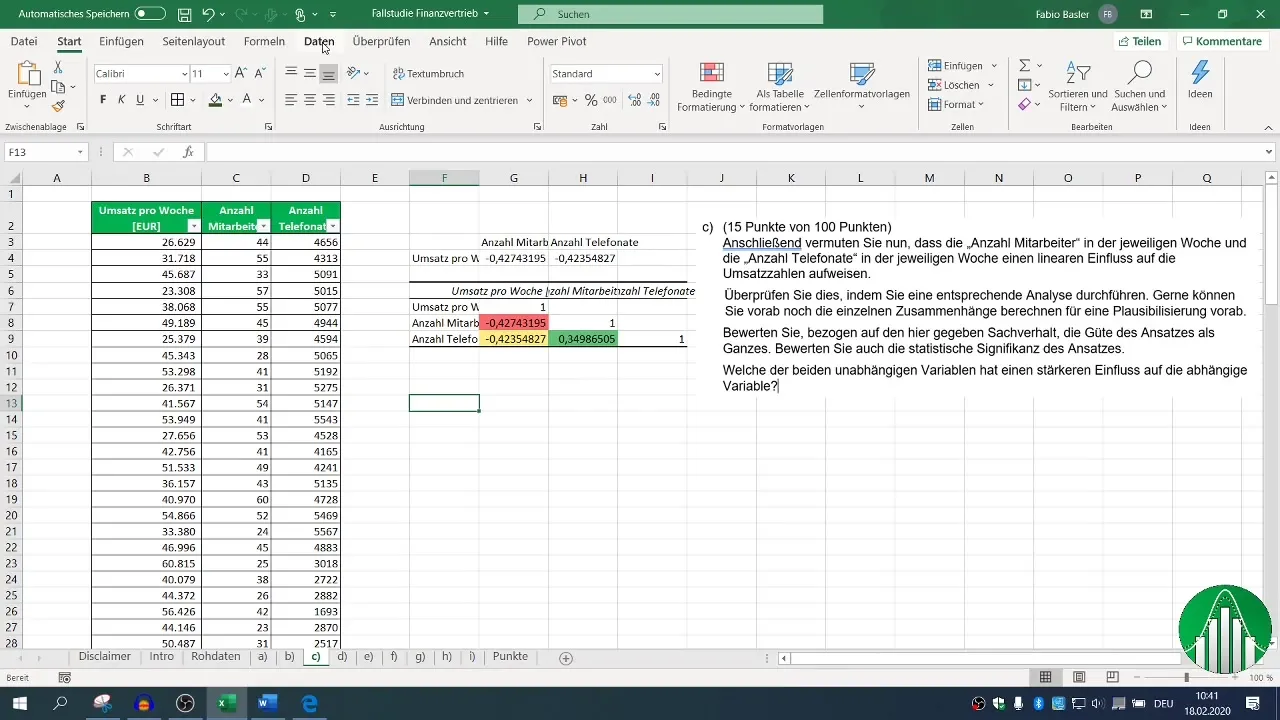
Norėdami išanalizuoti kintamųjų apyvartos, darbuotojų ir telefono skambučių koreliaciją, galite apskaičiuoti koreliacijos koeficientą. Norėdami tai padaryti, "Excel" programoje naudokite formulę =CORREL(). Norėdami apžvelgti visus kintamuosius, sukurkite koreliacijos matricą.
Pirmiausia pasirinkite atitinkamus apyvartos ir darbuotojų skaičiaus stulpelius. Naudodami formulę =CORREL( pasirinkite apyvartos ir darbuotojų skaičiaus intervalus. Rezultatas parodo, kokia stipri yra koreliacija.
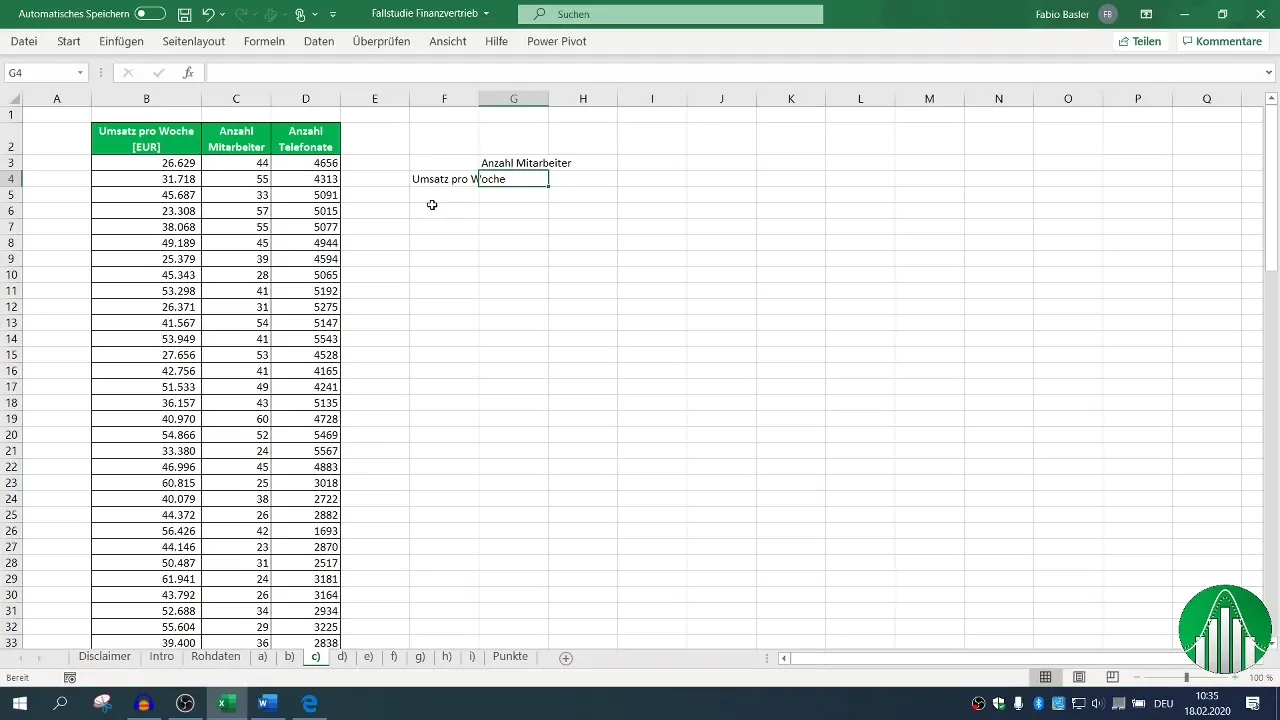
3. Koreliacijos matricos kūrimas
Norėdami atlikti išsamesnę analizę, rekomenduojame naudoti "Excel" duomenų analizės funkcijas. Jei dar to nepadarėte, įjunkite duomenų analizės funkciją. Eikite į skirtuką "Duomenys", spustelėkite "Duomenų analizė" ir pasirinkite "Koreliacija".
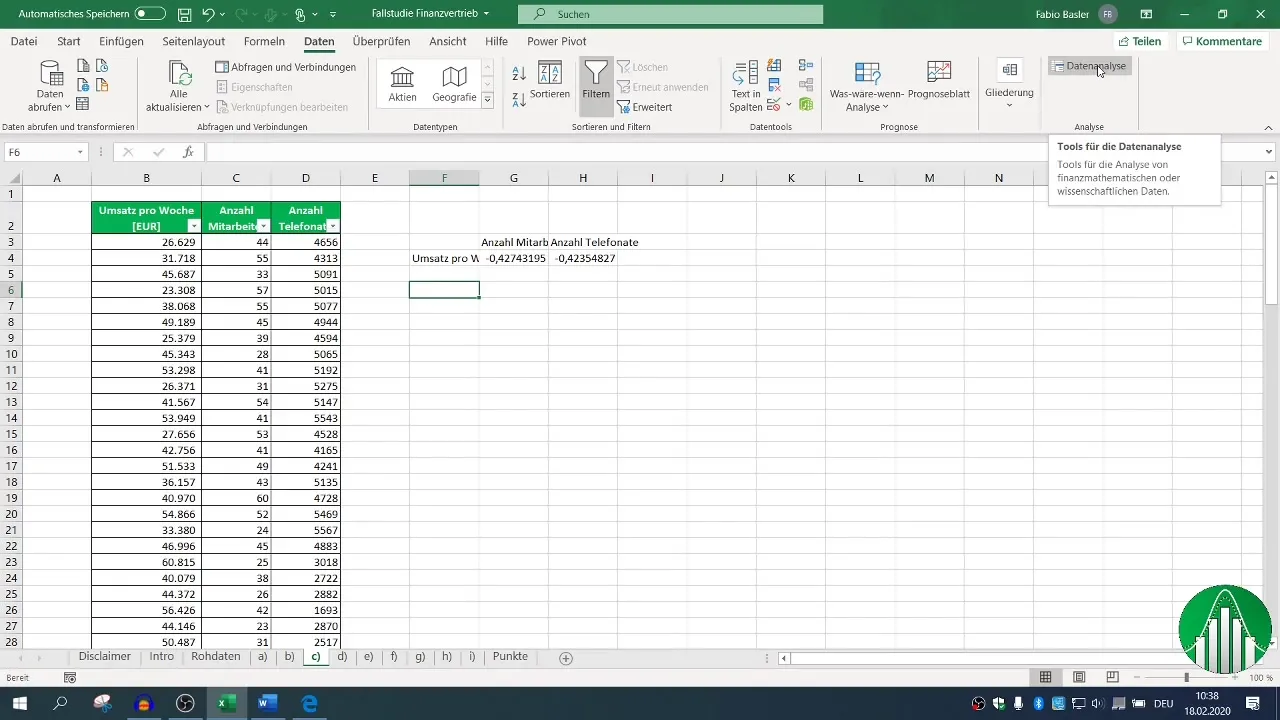
Nustatykite duomenų įvesties intervalą ir pažymėkite antraštės žymimąjį langelį, kad "Excel" teisingai atpažintų etiketes. Apibrėžę išvesties diapazoną, galite sukurti koreliacijos matricą, kurioje matysite visus svarbius ryšius.
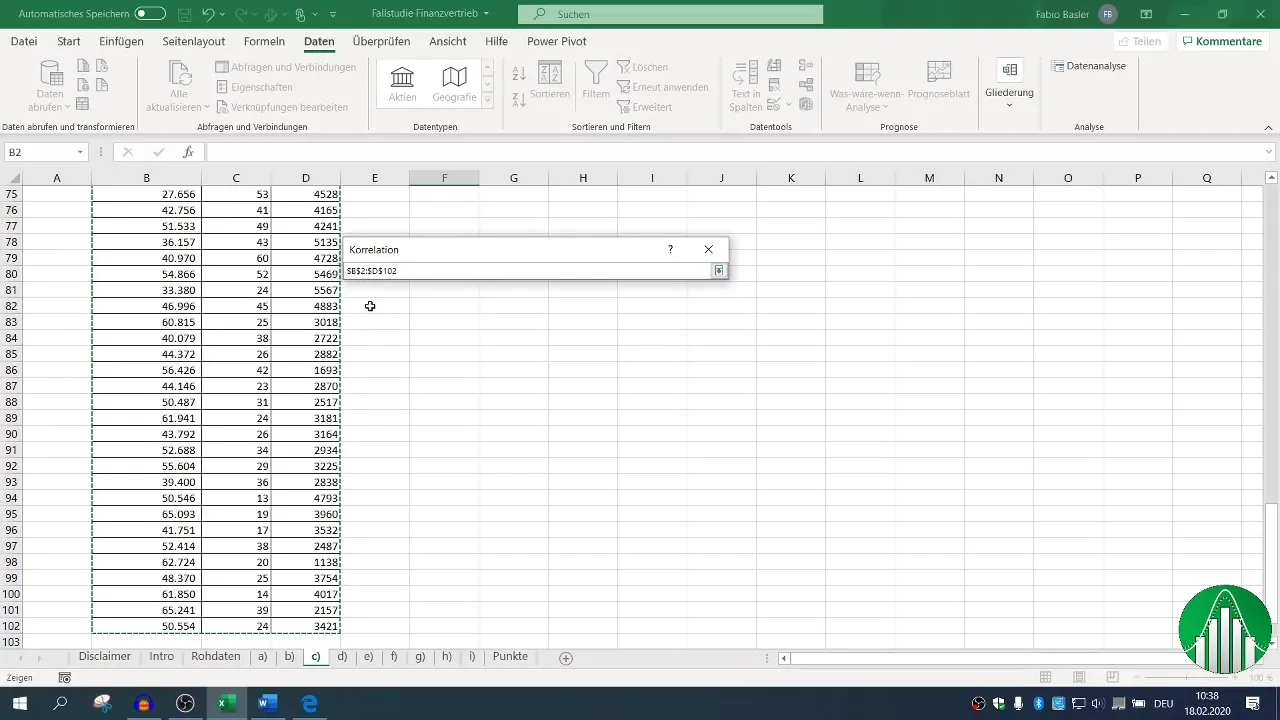
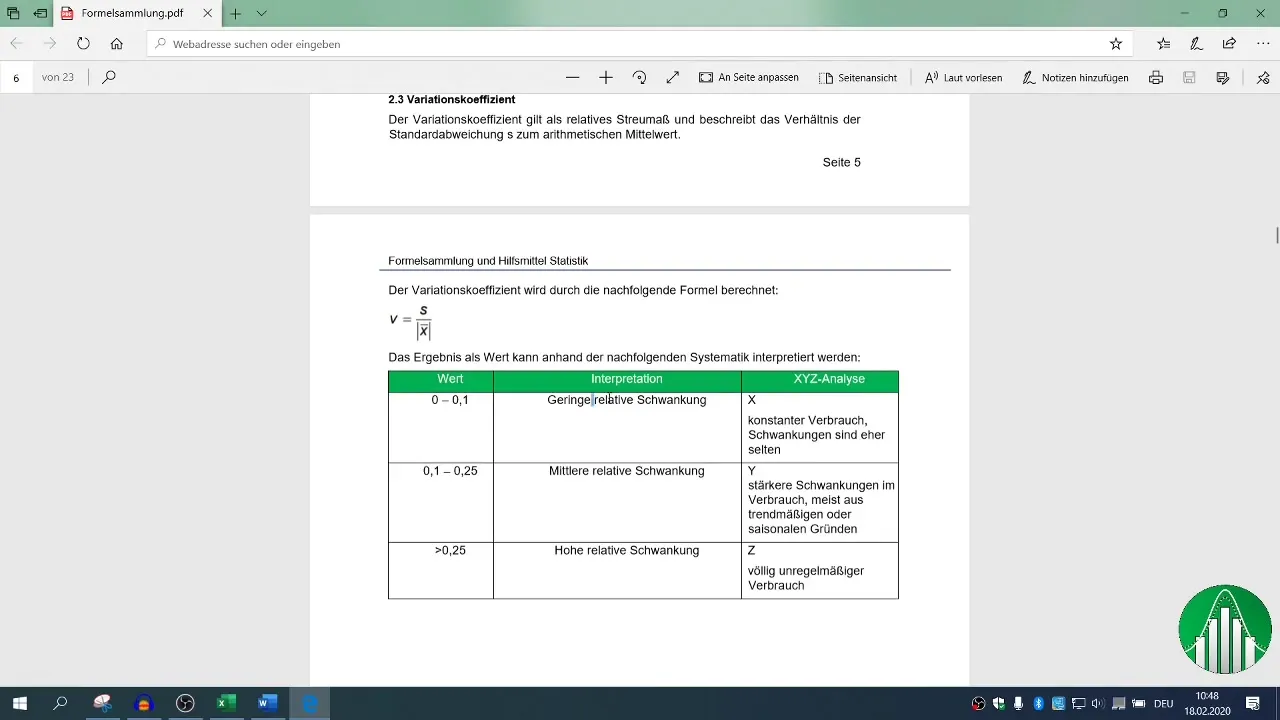
4. Koreliacijų vizualizavimas
Kad rezultatai būtų aiškesni, gali būti naudingas grafinis vaizdavimas naudojant XY diagramą. Pasirinkite X ir Y duomenis ir sugeneruokite taškų debesį.
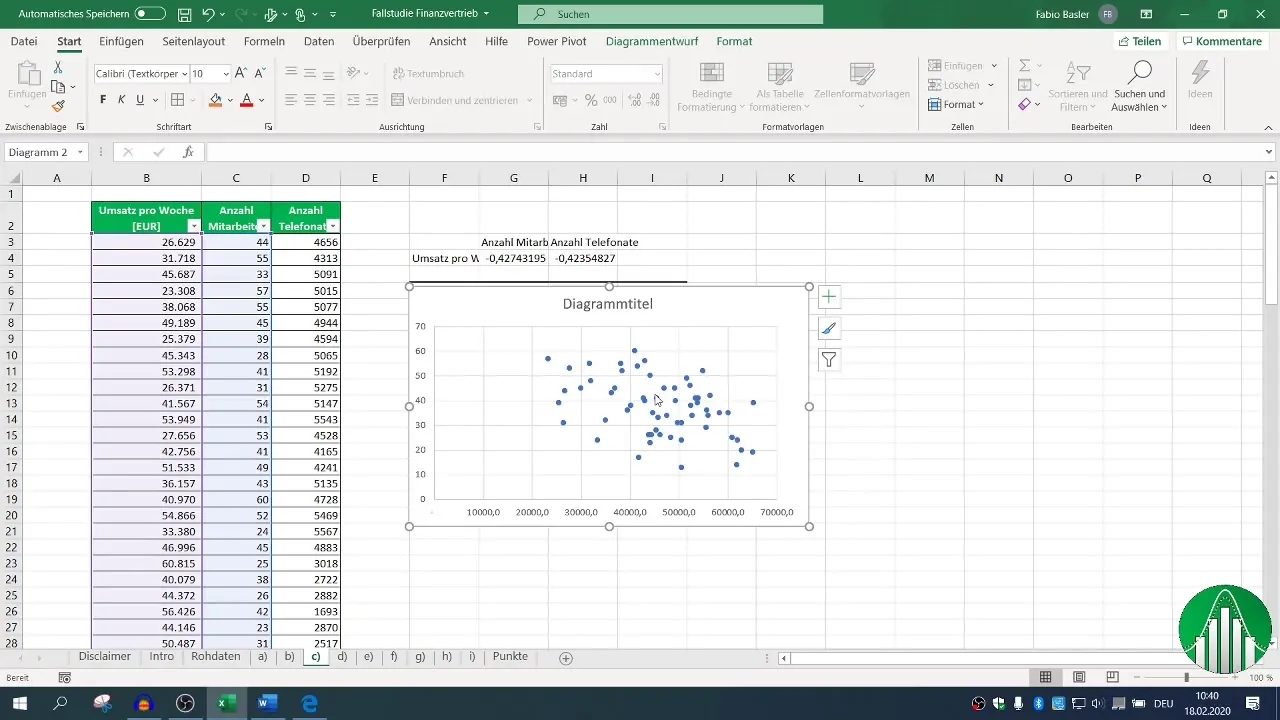
Norėdami vizualizuoti ryšį, pridėkite tendencijos liniją. Tai gali padėti intuityviau pažvelgti į duomenis.
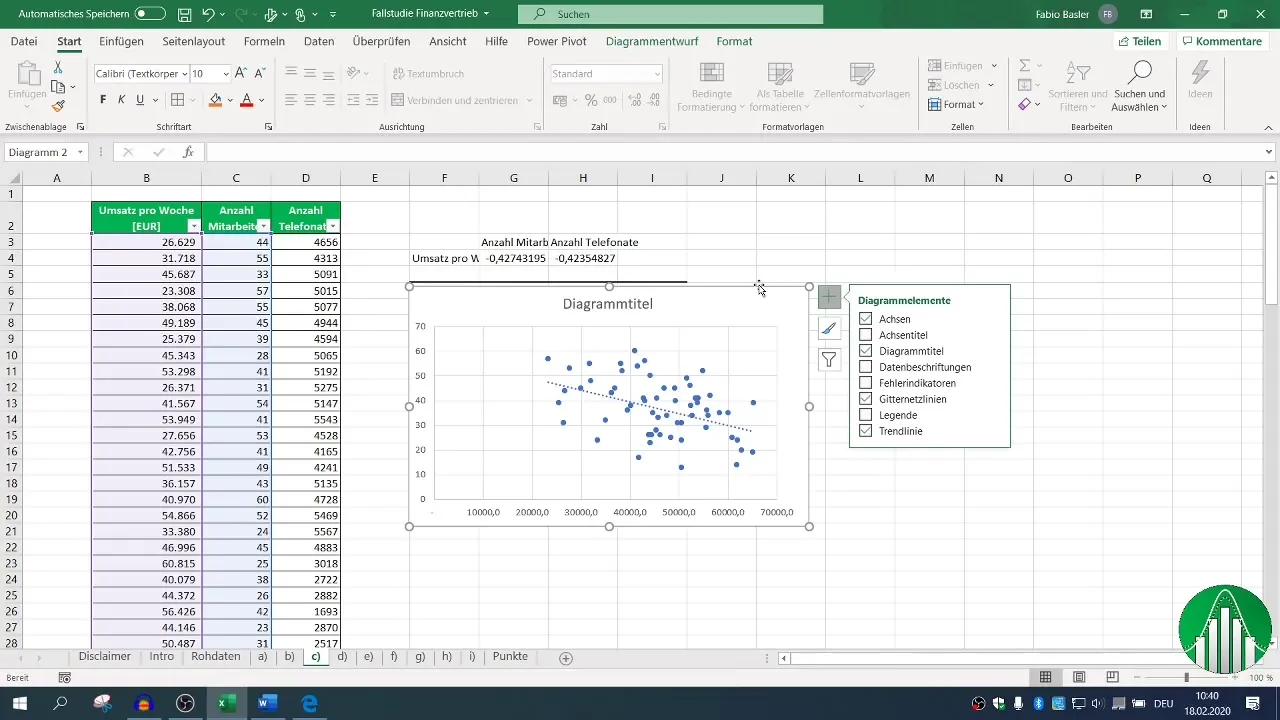
5. Regresinės analizės atlikimas
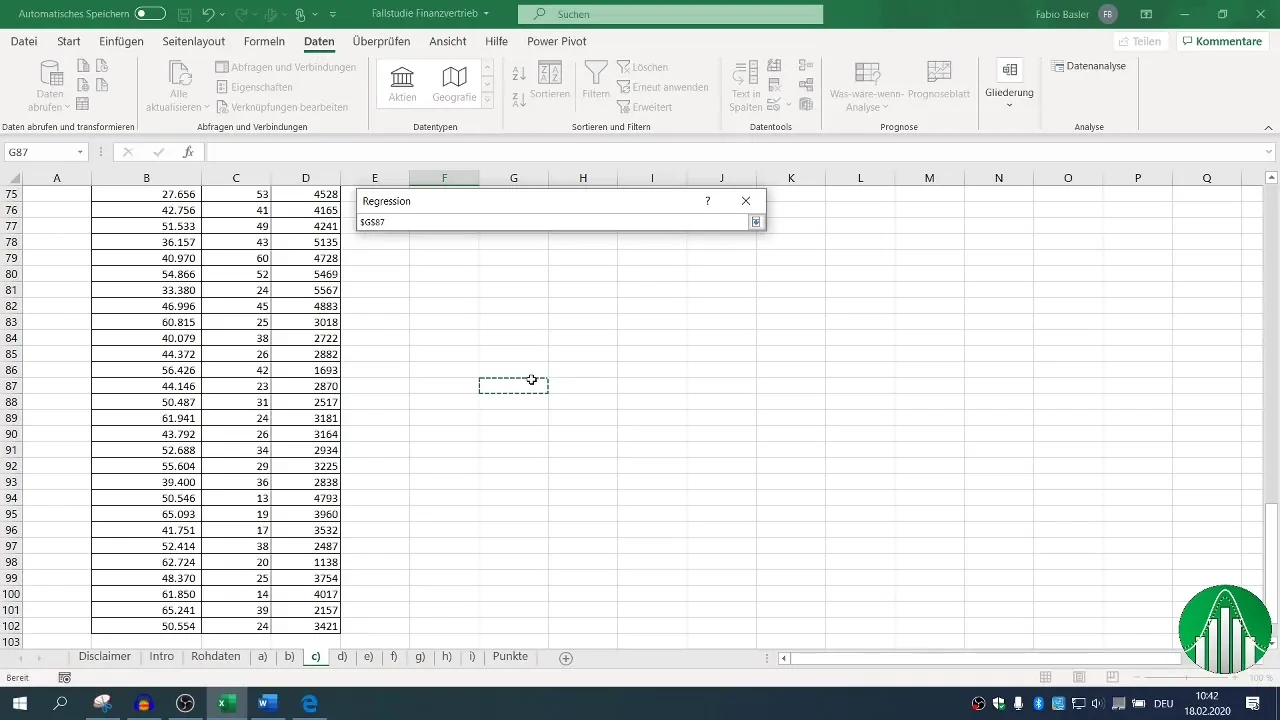
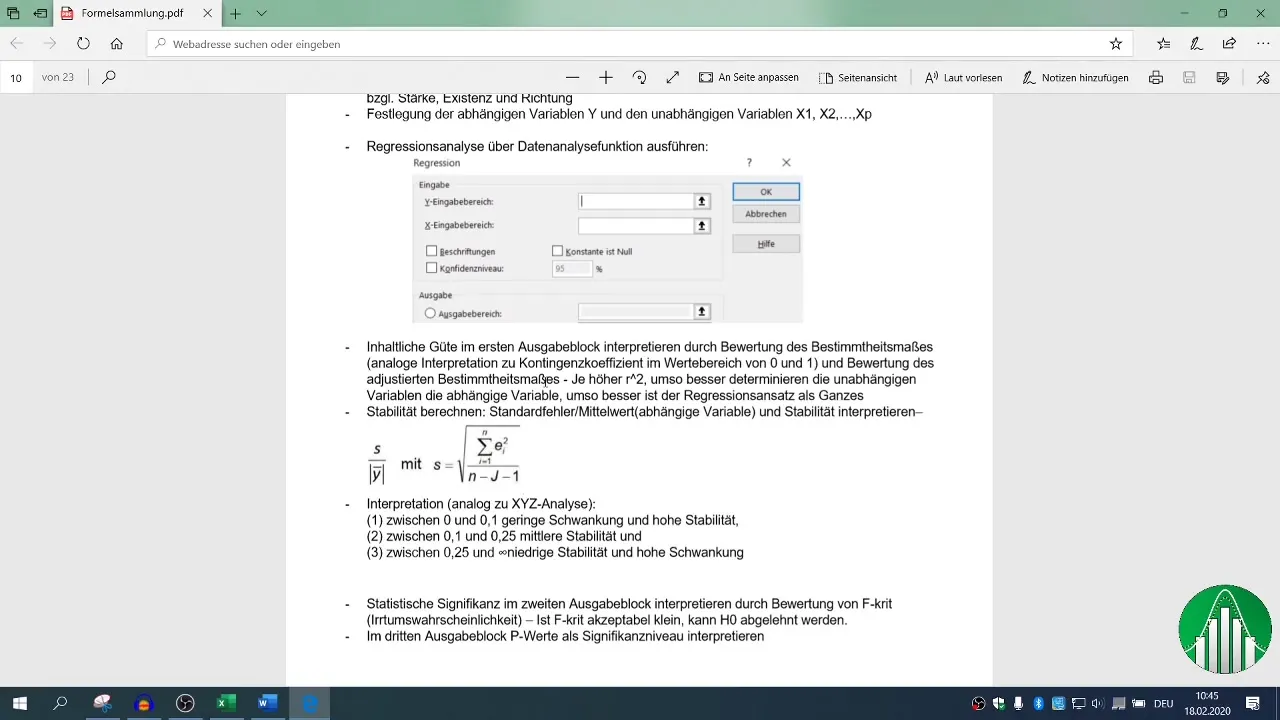
Dabar seka regresinės analizės etapas. Vėl eikite į "Data" (duomenys) ir pasirinkite "Data analysis" (duomenų analizė), tada "Regression" (regresija). Čia galite apibrėžti priklausomą kintamąjį (apyvarta) ir nepriklausomus kintamuosius (darbuotojų skaičius ir telefono skambučiai) įvesties sričiai.
Įsitikinkite, kad nustatyta reikšmių antraštė, ir apibrėžkite išvesties sritį. Pagal nutylėjimą nustatytas 95 % patikimumo lygis, kurio pakanka daugumai analizių.
6. Regresinės analizės vertinimas
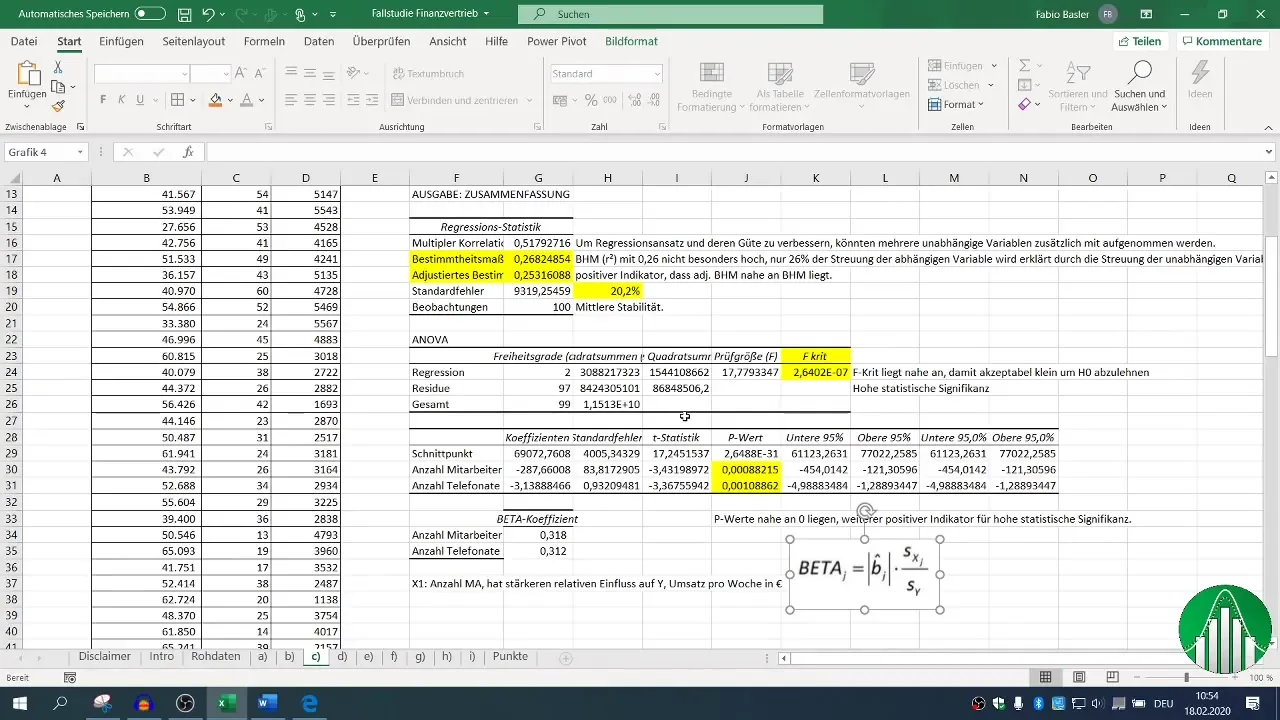
Atlikę regresiją, galite naudotis įvairiais išvesties blokais. Sutelkite dėmesį į determinacijos koeficientą (R²), kuris apibūdina modelio kokybę. R² 0,26 reiškia, kad nepriklausomi kintamieji paaiškina tik 26 % pardavimų kintamumo.
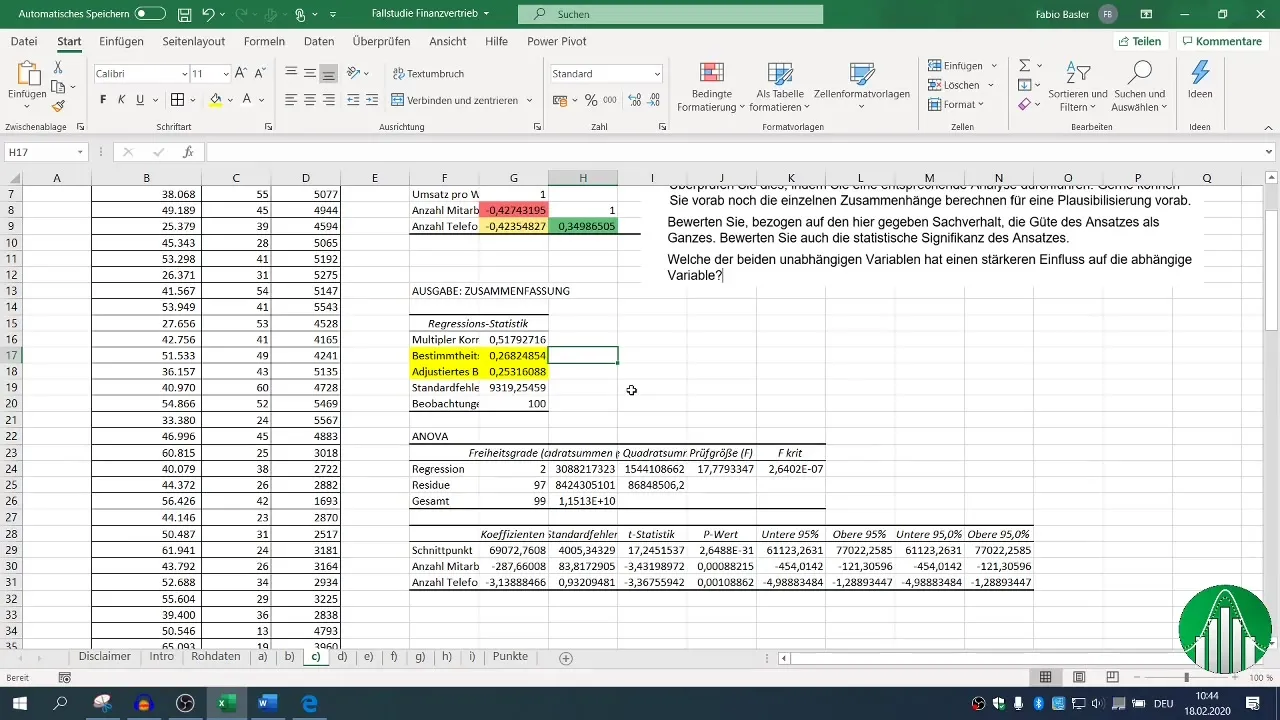
Pakoreguotas determinacijos koeficientas turėtų būti artimas R², kuris šiuo atveju yra teigiamas rodiklis.
7 Įvertinkite statistinį reikšmingumą
Nepriklausomų kintamųjų F reikšmė ir p reikšmės yra labai svarbios norint įvertinti jūsų modelio statistinį reikšmingumą. Mažesnė nei 0,05 p reikšmė rodo, kad ryšys yra statistiškai reikšmingas.
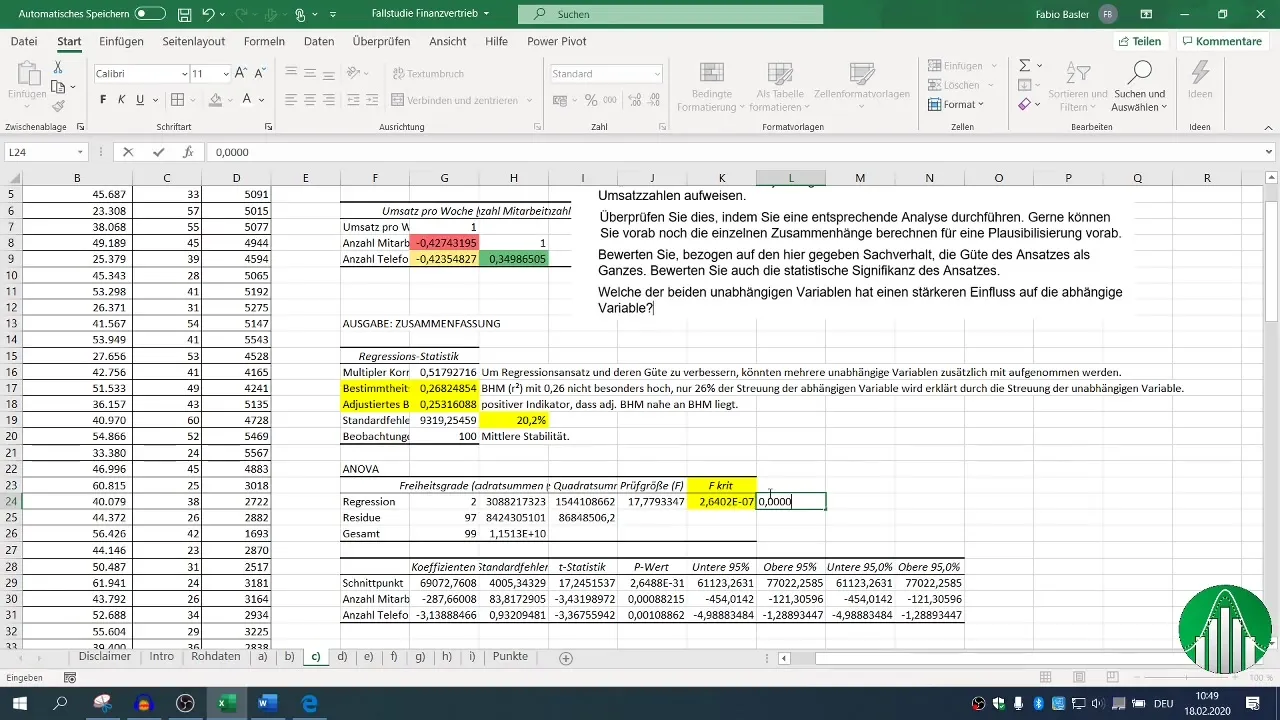
Šių statistinių parametrų įvertinimas kartu su R² padeda suprasti savo rezultatų stabilumą ir reikšmingumą.
8 Įtakos turinčių veiksnių palyginimas
Galiausiai jus domina, kuris veiksnys - darbuotojų skaičius ar telefono skambučiai - turi didesnę įtaką pardavimo rodikliams. Šiuo atveju paimkite beta koeficientus ir juos palyginkite.
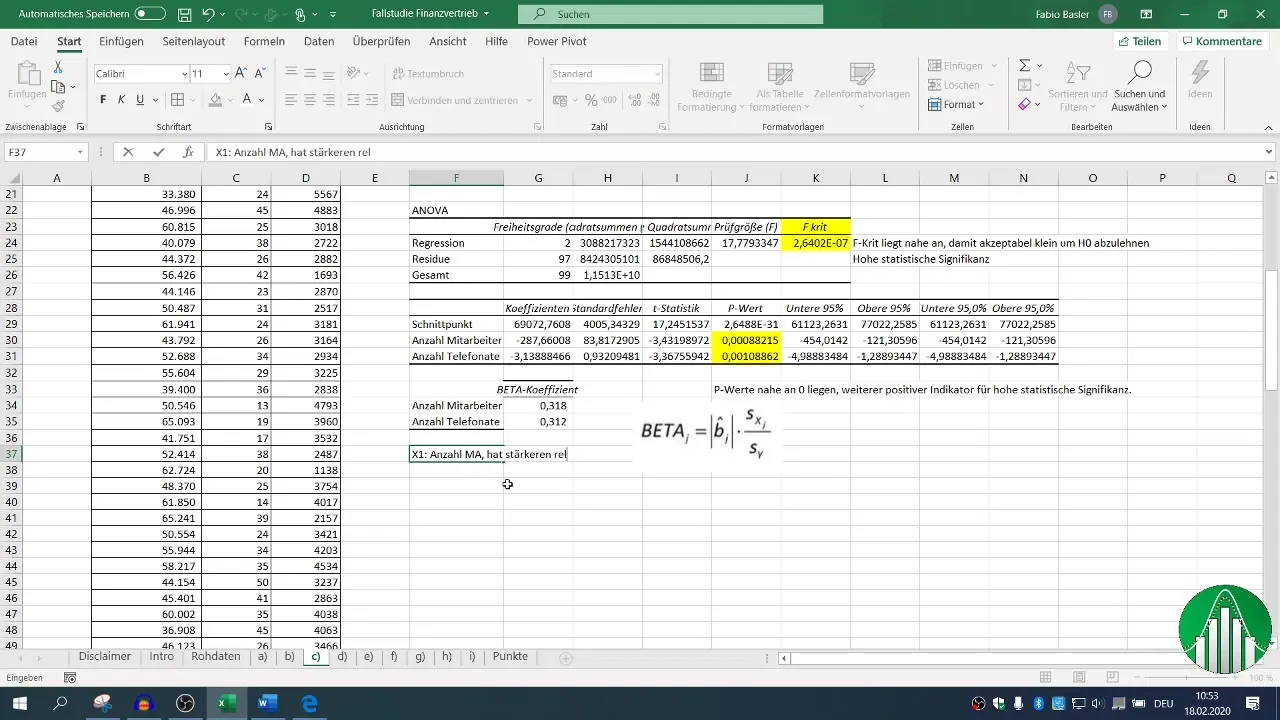
Didesnis beta koeficientas rodo santykinę įtaką; gali paaiškėti, kad darbuotojų skaičius turi didesnę įtaką apyvartai nei telefono skambučių skaičius.
Apibendrinimas
Ankstesnė analizė suteikė vertingų žinių apie statistinius kintamųjų apyvartos, darbuotojų skaičiaus ir telefono skambučių ryšius. Sistemingai atlikdami koreliacinę ir regresinę analizę "Excel" programoje, remdamiesi gautais rezultatais galite priimti pagrįstus sprendimus.
Dažniausiai užduodami klausimai
Kodėl svarbi koreliacinė analizė? Koreliacinė analizė padeda atpažinti dviejų kintamųjų ryšį prieš atliekant išsamią regresinę analizę.
Kaip aiškinti regresinės analizės R²? 0,26 R² reiškia, kad 26 % priklausomo kintamojo (pardavimų) variacijos paaiškina nepriklausomi kintamieji.
Kuo skiriasi koreliacija ir regresija? Koreliacija matuoja dviejų kintamųjų ryšį, o regresija įvertina kelių nepriklausomų kintamųjų poveikį priklausomam kintamajam.
Kaip galima patikrinti statistinį reikšmingumą? Statistinį reikšmingumą tikrinate naudodami p reikšmę; p reikšmės, mažesnės nei 0,05, laikomos reikšmingomis.
Kokį vaidmenį atlieka beta koeficientai? Beta koeficientai parodo santykinę nepriklausomų kintamųjų įtaką priklausomam kintamajam.


