Statistika ir svarīgs analīzes instruments daudzās jomās. Šajā rokasgrāmatā ir parādīts, kā veikt Spīrmena rangu korelācijas analīzi programmā Excel. Šī metode ļauj efektīvi kvantificēt sakarības starp kārtas mainīgajiem. Mēs aplūkojam saistību starp klientu apmierinātību un mārketinga līmeni.
Galvenie secinājumi
- Spīrmena rangu korelācijas analīze ir īpaši piemērota ordinālās skalas datiem.
- Excel programmas izmantošana ļauj ātri aprēķināt un vizualizēt rangu korelāciju.
- Vāja pozitīvā korelācija starp mārketinga līmeņiem un klientu apmierinātību liecina, ka lielāki ieguldījumi mārketingā ne vienmēr rada lielāku apmierinātību.
Soli pa solim
Pirmkārt, nav iespējams izvairīties no attiecīgo datu ievietošanas. Mēs koncentrējamies uz klientu apmierinātību un mārketinga līmeņiem. Šie dati tika savākti kā daļa no gadījuma pētījuma.
Varat sākt, kopējot datus no neapstrādāto datu kopas un ielīmējot tos jaunā darba cilnē. Pārliecinieties, ka ir skaidri definēti kolonnu virsraksti. Būtu noderīgi nosaukt kolonnas "Klientu apmierinātība" un "Mārketinga līmenis".
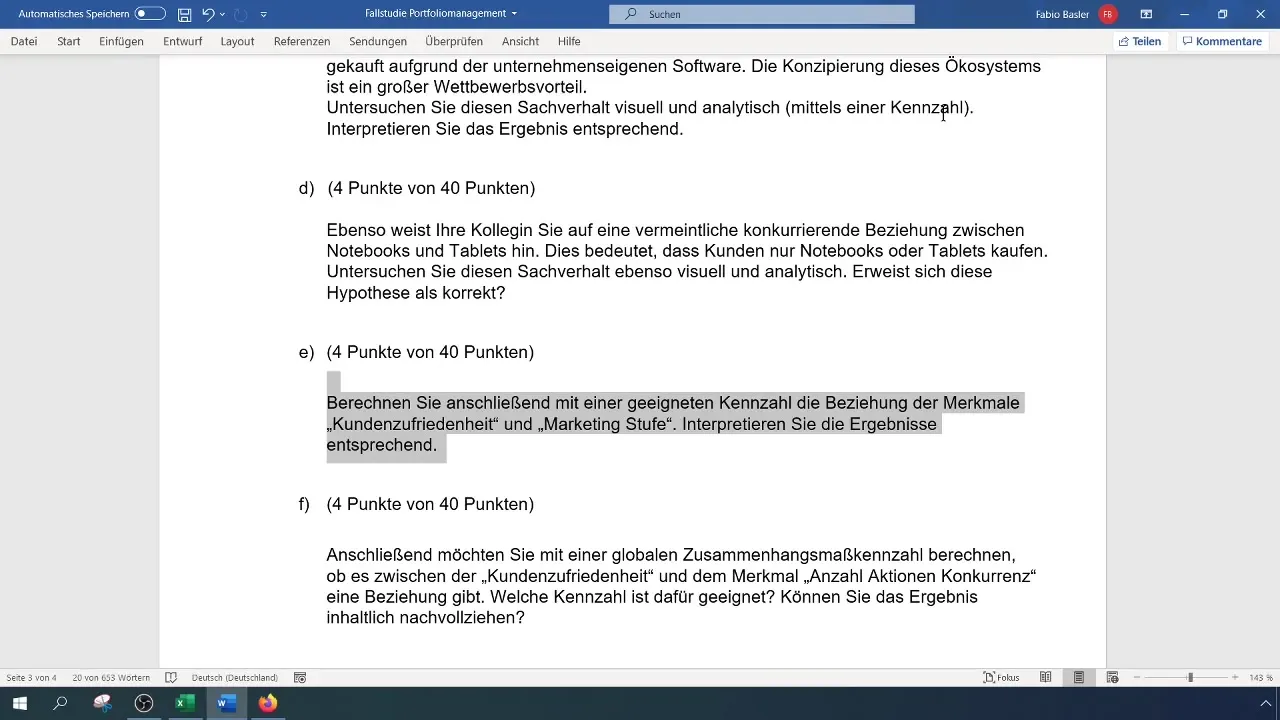
Kad esat nokopējuši datus, ir svarīgi pārbaudīt mainīgo lielumu skalas līmeņus. Klientu apmierinātība ir kārtas skala, bet mārketinga līmeņi arī ir kārtas kategoriju skala. Jums jāpārbauda, vai esat to pareizi sapratuši, lai izvairītos no kļūdām vēlākajos aprēķinos.
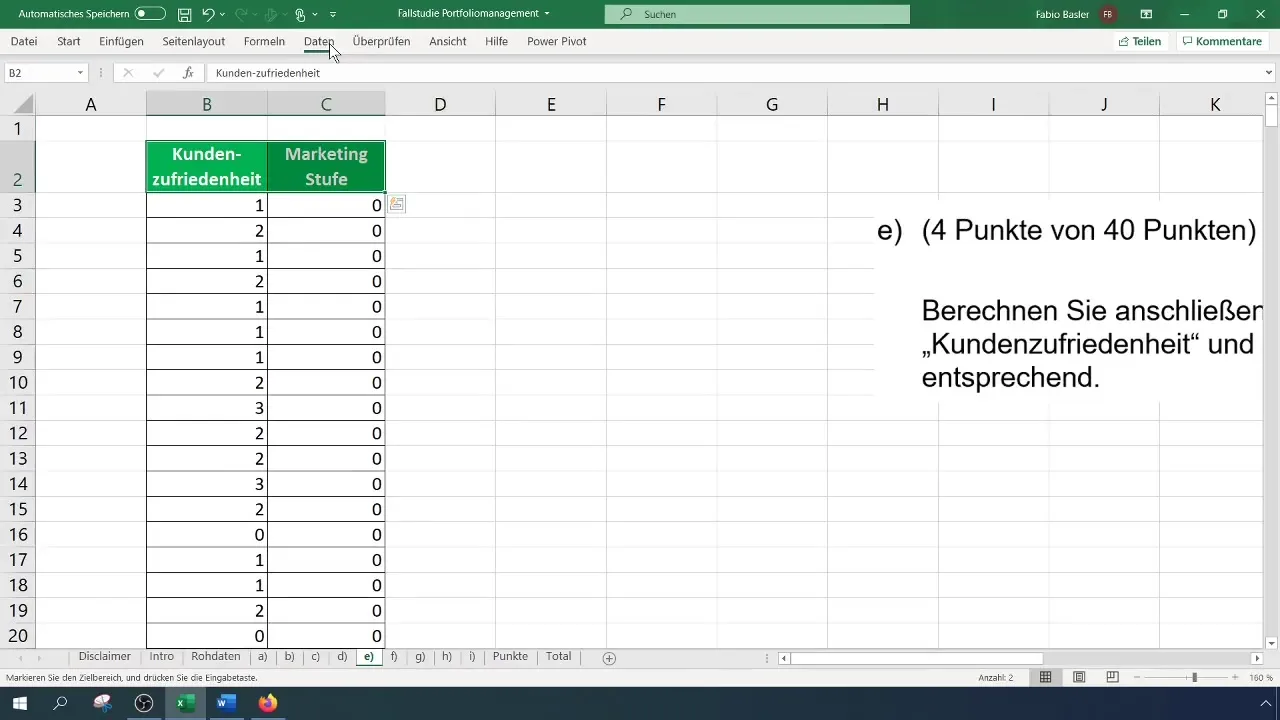
Nākamais solis ir sagatavot datus rangu korelācijas analīzei. Jums ir vajadzīgas mainīgo rangu vērtības. Excel programmā to veic, izmantojot funkciju "RANK.EQUAL" vai "RANK.AVERAGE.W". Šī funkcija katram skaitlim piešķir rangu attiecībā pret norādīto matricu. Pārliecinieties, ka strādājat pareizajā diapazonā.
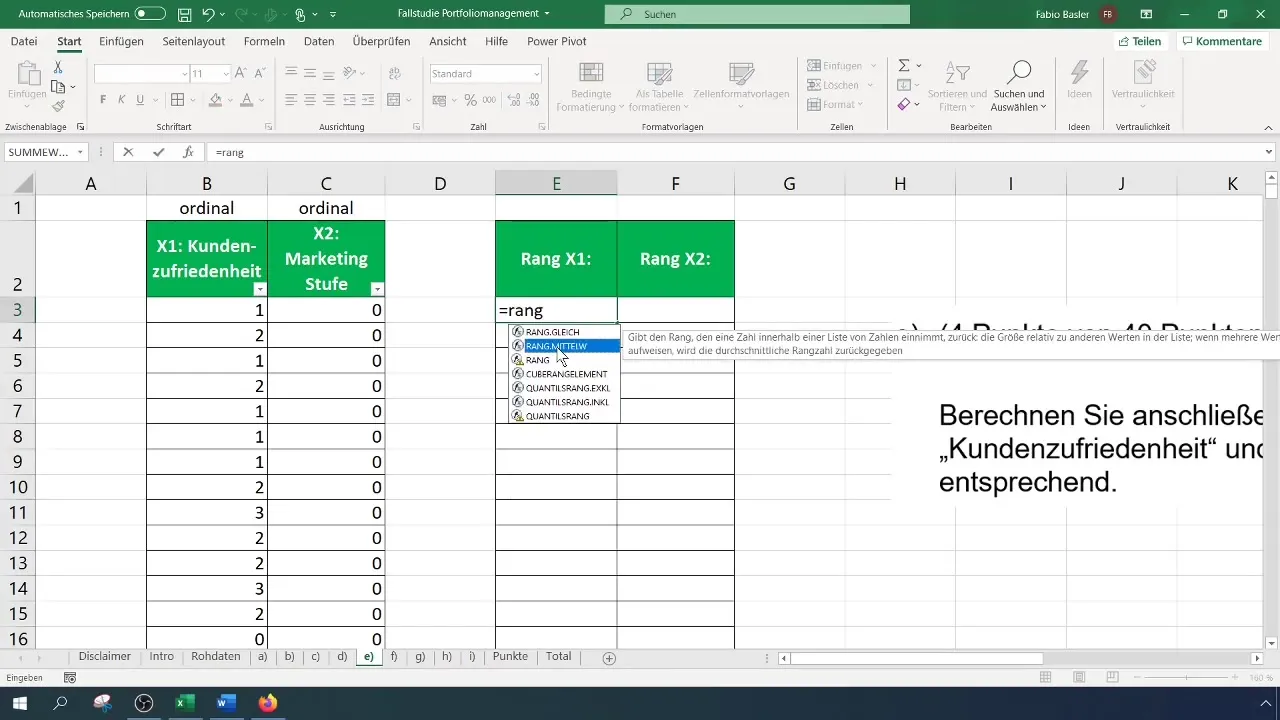
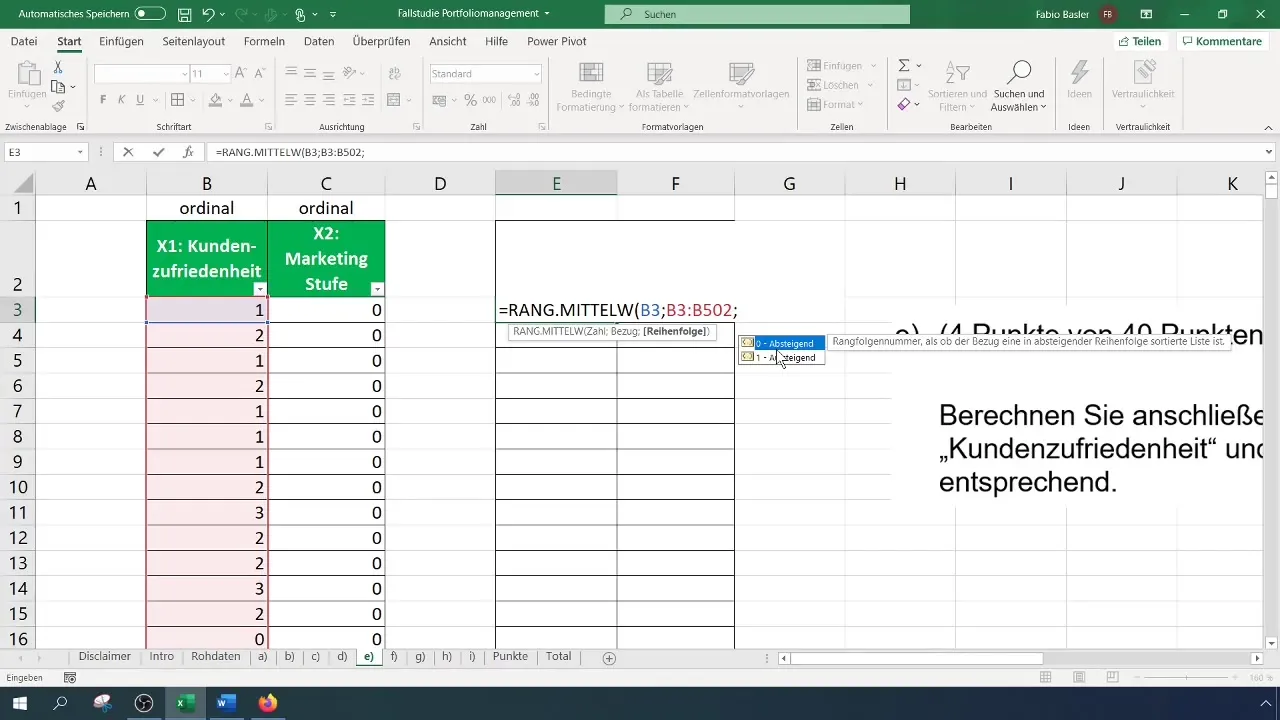
Lai aprēķinātu rangus klientu apmierinātībai, ko šeit apzīmēsim ar mainīgo X1, vispirms izvēlieties attiecīgo šūnu. Pirmajam novērojumam tas nozīmē, ka jāizvēlas šūna klientu apmierinātībai un pēc tam jāizvēlas matrica, kurā tiek noteikti rangi. Svarīgi ir noteikt atsauci visai matricai, lai atsauce nemainītos, velkot formulu uz leju.
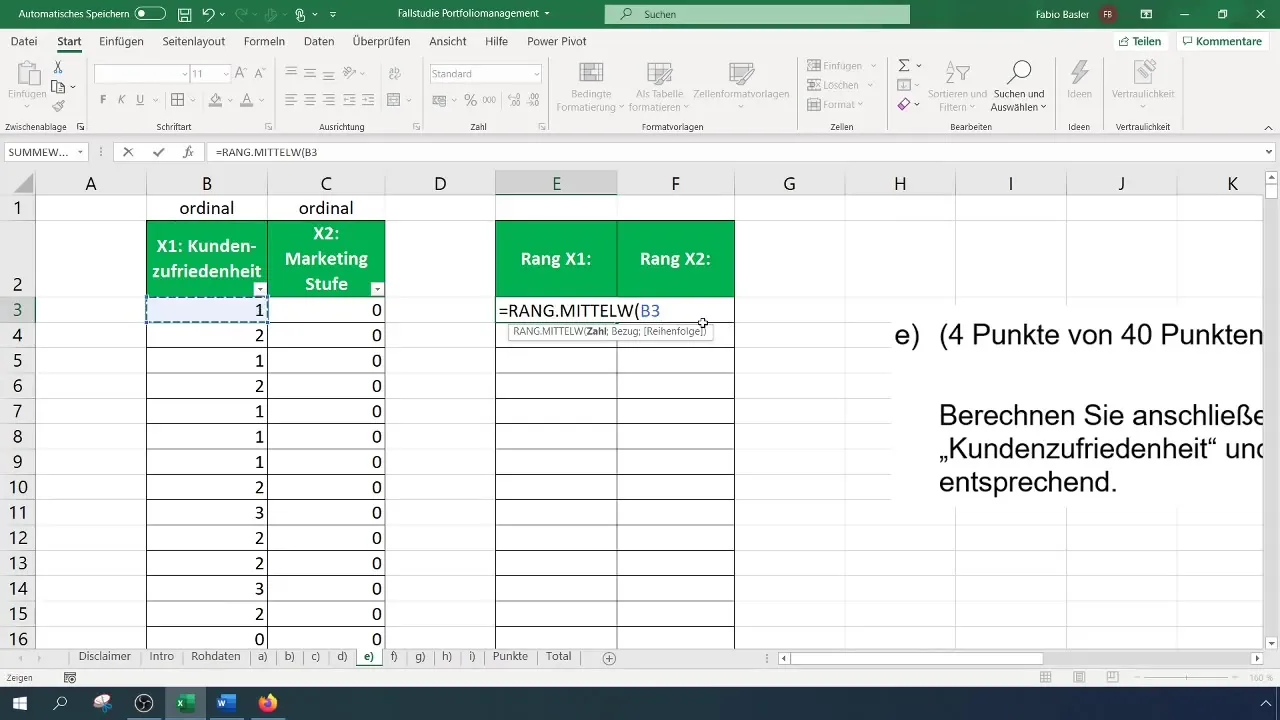
Sāciet aprēķinu, ievadot formulu un pēc tam pievienojot atbilstošos parametrus. Pārliecinieties, ka funkcijā ir ievērota pareizā secība. Nosakiet atsauci uz datu matricu un atlasiet vēlamo šķirošanas secību, t. i., augošā vai dilstošā secībā.
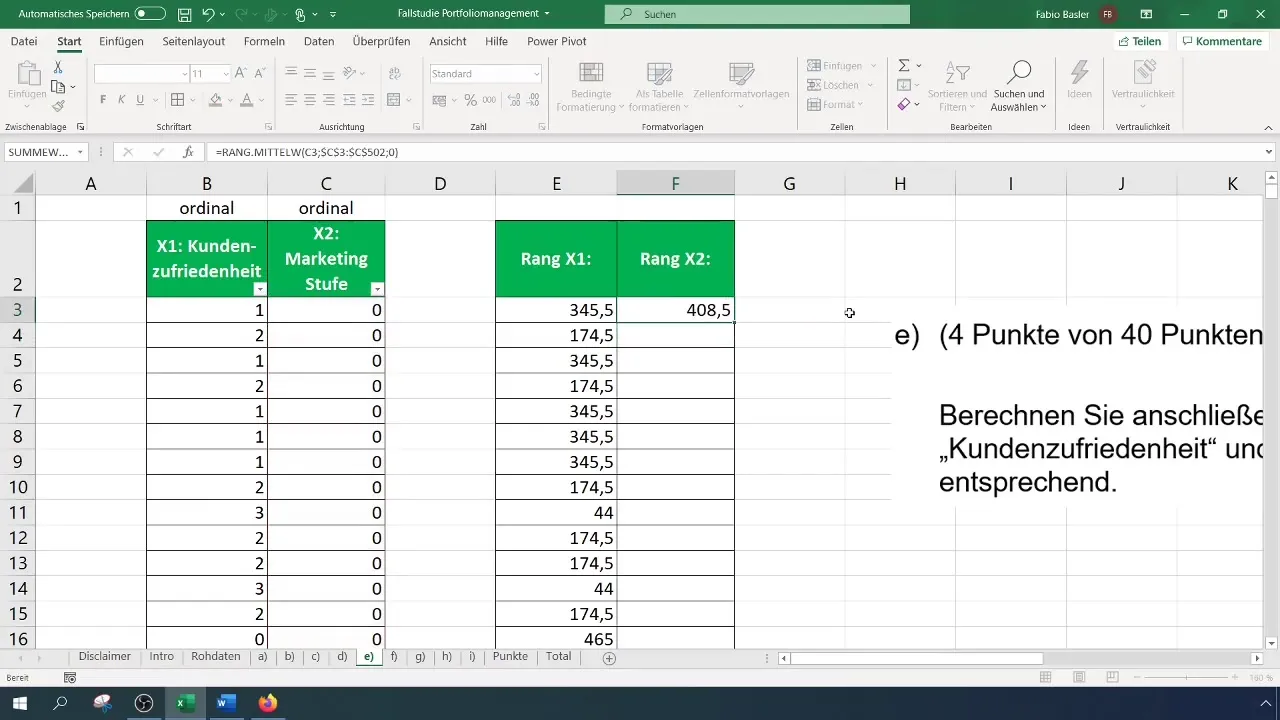
Ja vēlaties aprēķināt rangus mārketinga līmenim (X2), atkārtojiet to pašu procesu. Arī šajā gadījumā ir svarīgi saglabāt visu datu diapazonu, lai formula darbotos pareizi, kad to kopējat uz leju. Šie soļi nodrošina, ka rangi katram mainīgajam tiek aprēķināti pareizi.
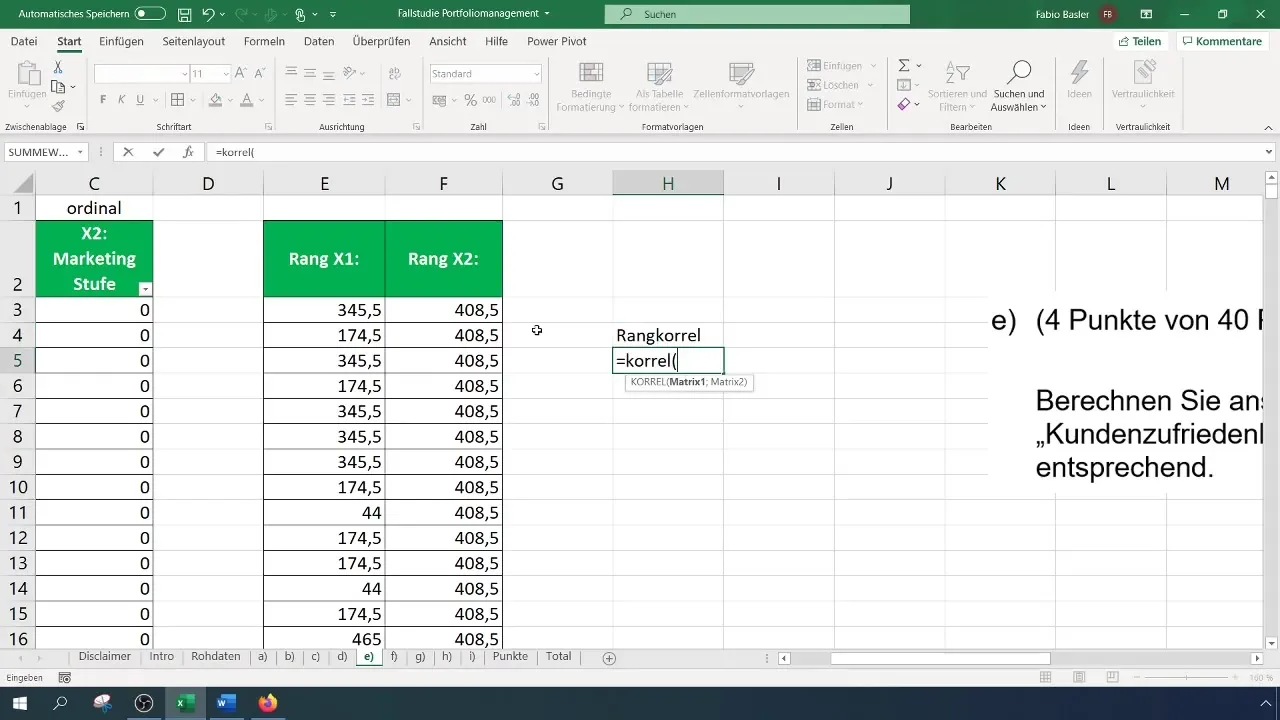
Kad esat ieguvuši abu mainīgo rangus, varat aprēķināt rangu korelāciju. To veic ar funkciju "CORREL". Šī funkcija ļauj izvēlēties gan X1, gan X2 rangus un aprēķināt korelāciju. Rezultāts parādīs, cik spēcīga ir korelācija starp abiem mainīgajiem.
Jūsu gadījumā korelācija ir 0,082, kas norāda uz vāju pozitīvu korelāciju. Šis skaitlis parāda, ka, lai gan pastāv tendence, ka lielāki mārketinga izdevumi rada lielāku klientu apmierinātību, šī korelācija nav spēcīga.
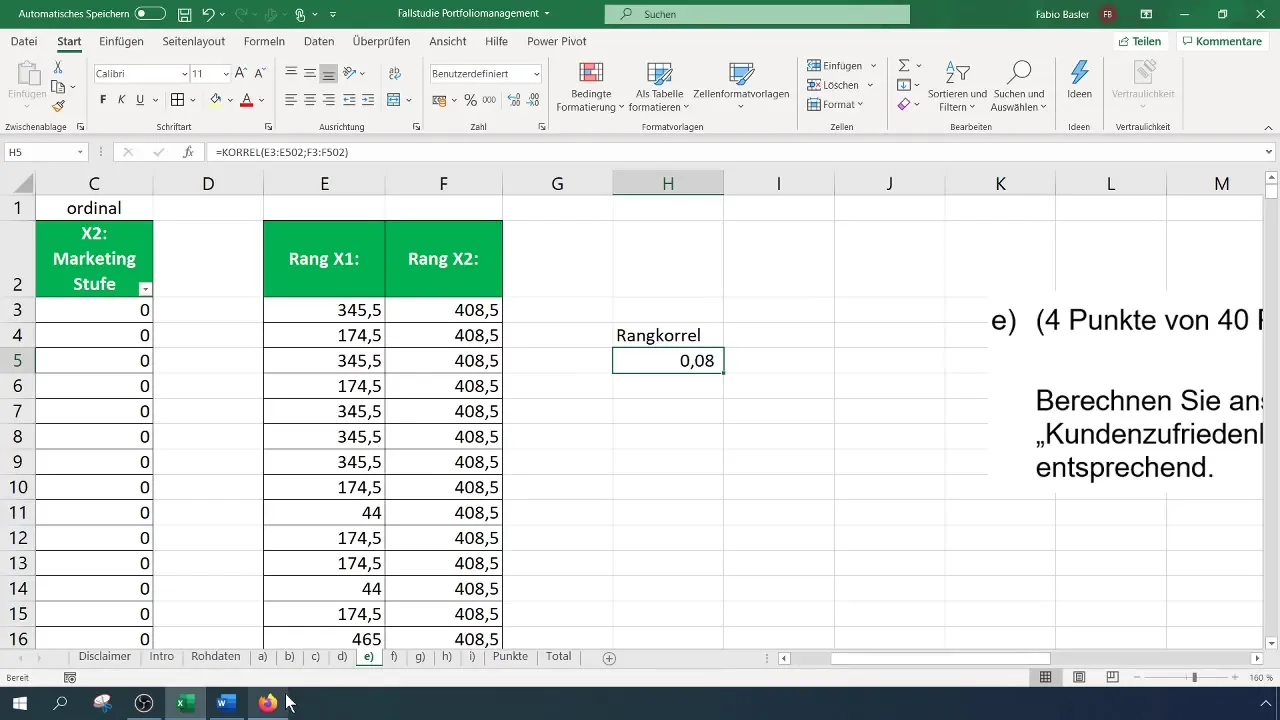
Visbeidzot, jums jādokumentē savu rezultātu interpretācija. Tabula varētu jums palīdzēt noskaidrot, kur ir ranga korelācija, un skaidri parādīt saistību starp abiem mainīgajiem.
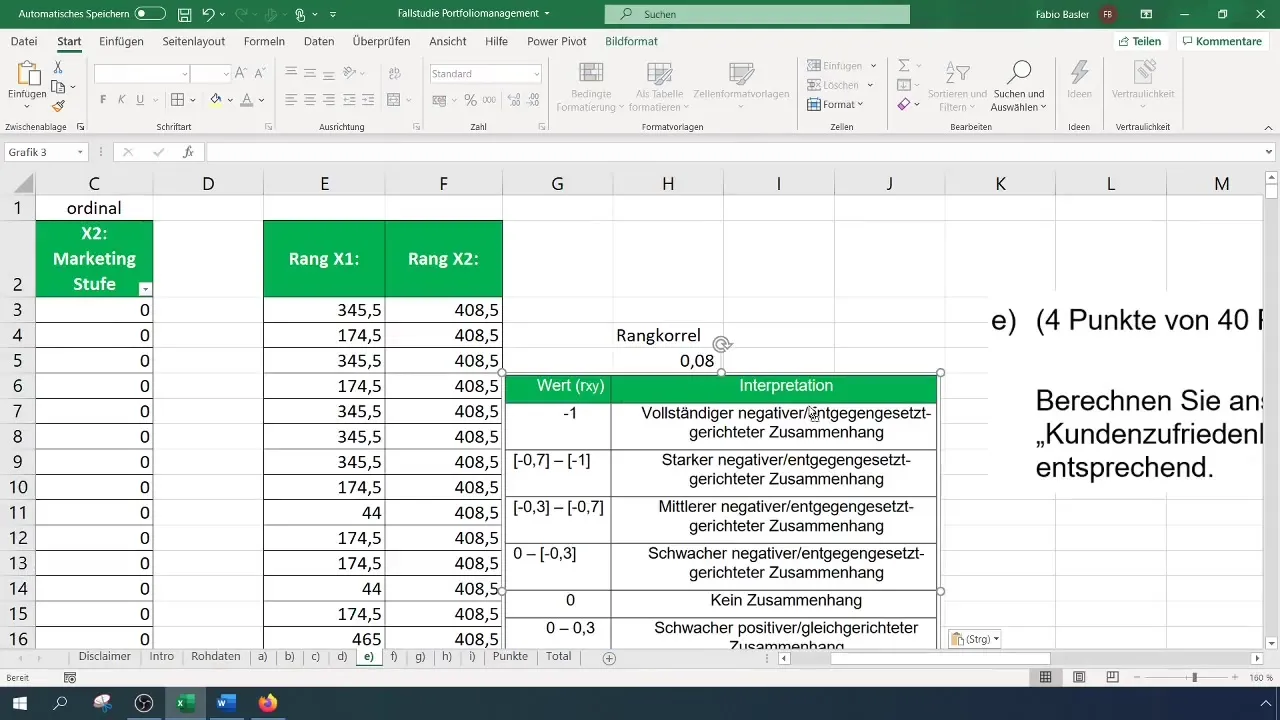
Ranga korelācijas analīzes pieeja palīdz iegūt kvalitatīvu ieskatu kvantitatīvajos datos un parāda, kā varētu mainīties mārketinga izdevumi, tieši nepalielinot klientu apmierinātību.
Kopsavilkums
Šajā rokasgrāmatā jūs uzzinājāt, kā veikt rangu korelācijas analīzi programmā Excel. Vispirms jūs pareizi sagatavojāt savus datus un pēc tam noteicāt abu mainīgo rangus. Visbeidzot, jūs aprēķinājāt rangu korelāciju, lai kvantitatīvi noteiktu saistību starp mārketinga līmeni un klientu apmierinātību.
Biežāk uzdotie jautājumi
Ar ko atšķiras Spearman un Kendall? Spearman un Kendall ir rangu korelācijas koeficienti, taču tos aprēķina atšķirīgi. Spearman balstās uz rangu atšķirībām, bet Kendall izmanto sakritību un neatbilstību skaitu.
Kā izvēlēties piemērotu korelāciju? Korelācijas izvēle ir atkarīga no datu veida. Kārtības skalas datiem piemērots ir Spearman, bet metriskiem datiem bieži izmanto Pīrsonu.
Vai korelācijas vietā varētu izmantot regresiju? Jā, regresija var būt noderīga, lai analizētu viena vai vairāku neatkarīgo mainīgo ietekmi uz atkarīgo mainīgo, korelācija parāda tikai saistību.


