Veiksmīgs sagaidāmās vērtības 1-SP tests programmā Excel

Statistiskie testi ir datu analīzes un lēmumu pieņemšanas galvenā sastāvdaļa. Īpaši biotehnoloģiju jomā var būt ļoti svarīgi pārbaudīt hipotēzes par aktīvo vielu sekmīgumu. Šajā pamācībā uzzināsiet, kā efektīvi veikt vienas izlases testu (1-SP testu) paredzamajai vērtībai ar zināmu dispersiju programmā Excel.

Galvenie secinājumi

Šajā rokasgrāmatā jūs uzzināsiet:

• 1-SP testa teorētisko pamatu.
• Testa veikšanas soļus programmā Excel.
• Rezultātu interpretācija.

Datu sagatavošana

Lai Excel programmā veiktu 1-SP testu, vispirms ir nepieciešami attiecīgie dati. Mūsu piemērā mēs pieņemam situāciju, kurā jūs analizējat aktīvo sastāvdaļu veiksmes koeficientu. Ir zināms, ka vidējais sekmīguma rādītājs mēdz būt 59 % ar standartnovirzi 19. Vispirms jums jāievada dati Excel izklājlapā.

Pārliecinieties, ka dati ir sakārtoti slejās, lai vēlāk tiem varētu piekļūt. Skaidrs pārskats palīdzēs jums vieglāk izprast atsevišķus soļus.

Testa pārskats

1-SP testu izmanto, lai pārbaudītu, vai vidējā veiksmes vērtība būtiski atšķiras no norādītās vērtības. Šajā gadījumā mēs pārbaudām, vai 59% veiksmes rādītāju nākotnē var ievērojami palielināt.

Hipotēžu formulēšana

Testam formulētajām hipotēzēm ir izšķiroša nozīme:

• Nulles hipotēze (H0): Patiesā sagaidāmā vērtība ir 59 (σ = 59%).
• Alternatīvā hipotēze (H1): Patiesā sagaidāmā vērtība ir lielāka par 59%.

Formulējot hipotēzes, galvenā uzmanība jāpievērš tam, kas tieši ir jāpārbauda un kā tas izpaužas jūsu kontekstā.

Ir svarīgi skaidri apzināties atšķirību starp nulles hipotēzi un alternatīvo hipotēzi, jo tās veido pamatu turpmākajiem aprēķiniem.

Izlases apkopošana

Mūsu testam mēs ņemam 500 aktīvo sastāvdaļu paraugu. Ir svarīgi atzīmēt, ka izlases atlase ir reprezentatīva un tai ar atbilstošas metodes palīdzību ir jāgarantē, ka jūsu rezultātus var reāli pārnest uz visu populāciju.

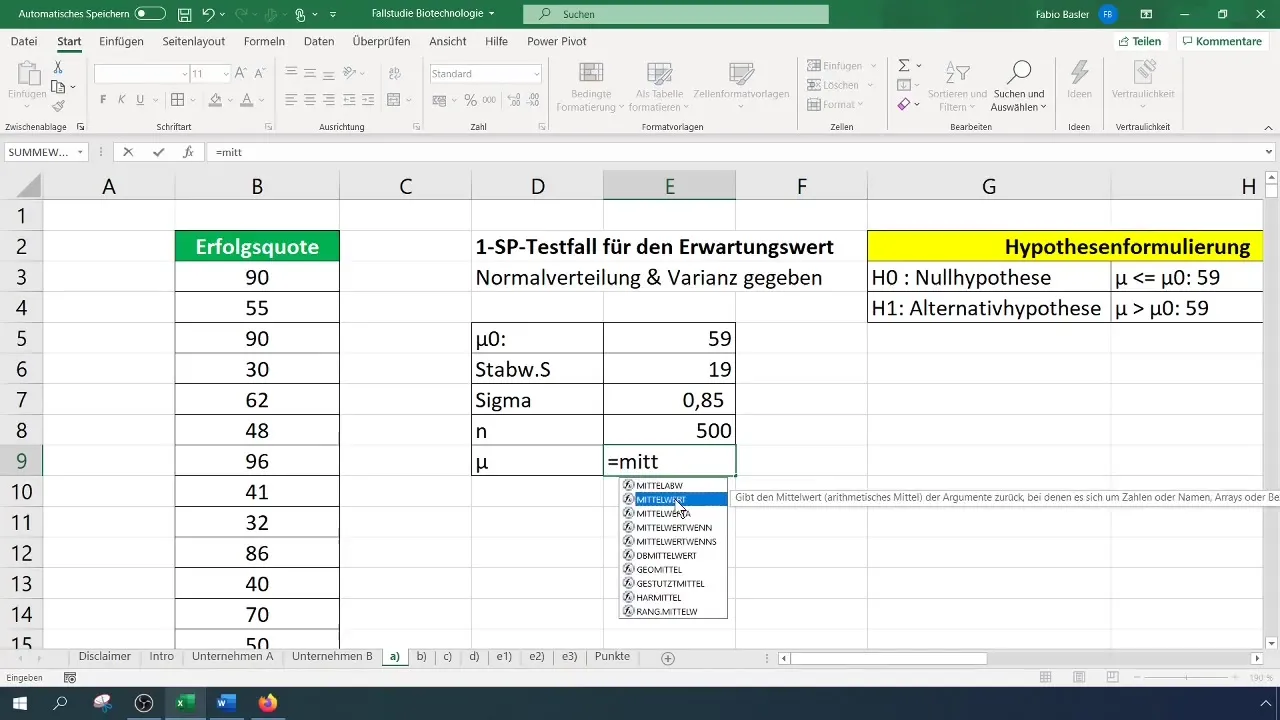
Lai veiktu testu, vispirms aprēķiniet vidējo aritmētisko vērtību. To var viegli izdarīt, izmantojot atbilstošu formulu programmā Excel.

Testa mainīgā lieluma aprēķināšana

Testa mainīgo 1-SP testam nosaka pēc šādas formulas

[ Z = \frac{\bar{x} - \mu_0}{\sigma/\sqrt{n}} ] ]

Šeit (\bar{x}) apzīmē jūsu parauga vidējo vērtību, (\mu_0) - pieņemto vidējo vērtību (šajā gadījumā 59), (\sigma) - standartnovirzi (šeit 19) un (n) - paraugu skaitu (500).

Pēc tam, kad formulā ir ievietotas vērtības, aprēķiniet testa statistiku, lai noteiktu, vai tā ir nozīmīga vai nav.

Kritiskās vērtības noteikšana

Ja nozīmīguma līmenis ir 1% (0,01), jums ir jānolasa vai jāaprēķina kritiskā vērtība. To var izdarīt programmā Excel, izmantojot funkciju NORM.S.INV.

Formula ir šāda:

S.INV}(1 - \alpha) ] [ \text{NORM.S.INV}(1 - \alpha)

Kur (\alpha) ir nozīmīguma līmenis (0,01). Noteikto vērtību izmanto par pamatu salīdzinājumam ar testa mainīgo.

Testa veikšana

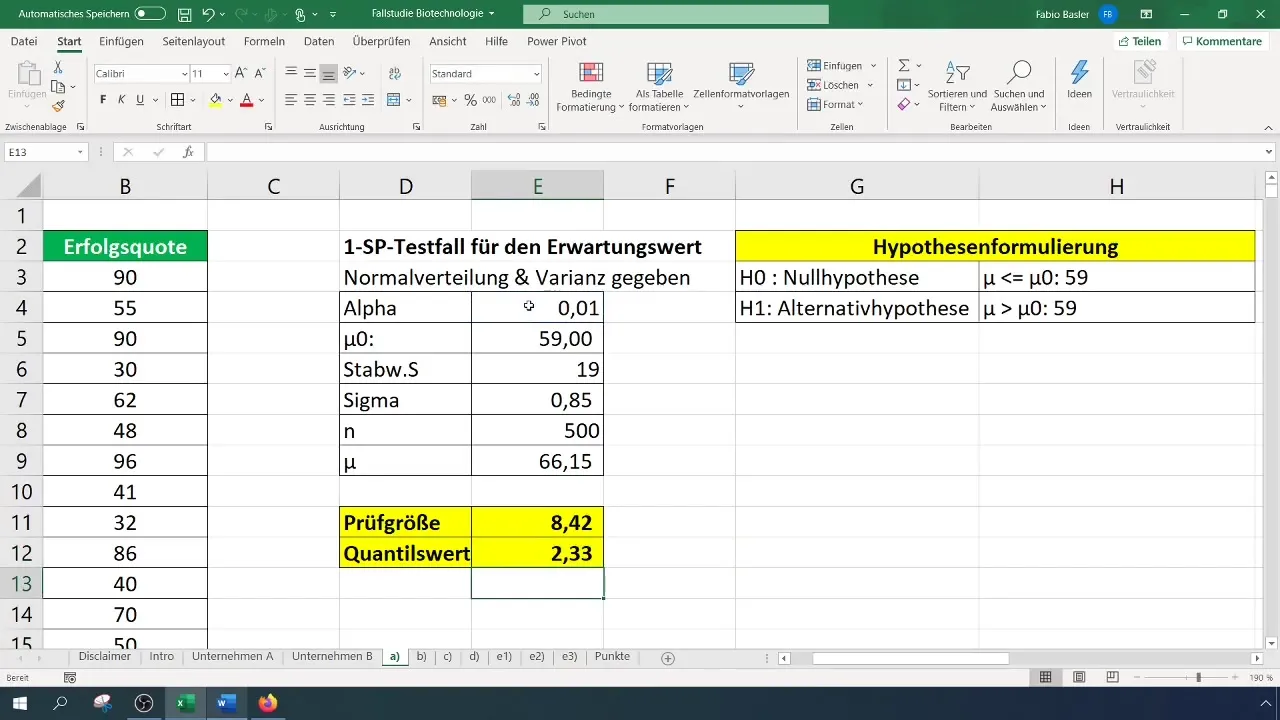
Tagad, kad jums ir gan testa statistika, gan kritiskā vērtība, salīdziniet abas:

• Ja testa statistika ir lielāka par kritisko vērtību, nulles hipotēze tiek noraidīta.
• Pretējā gadījumā nulles hipotēzi nevar noraidīt.

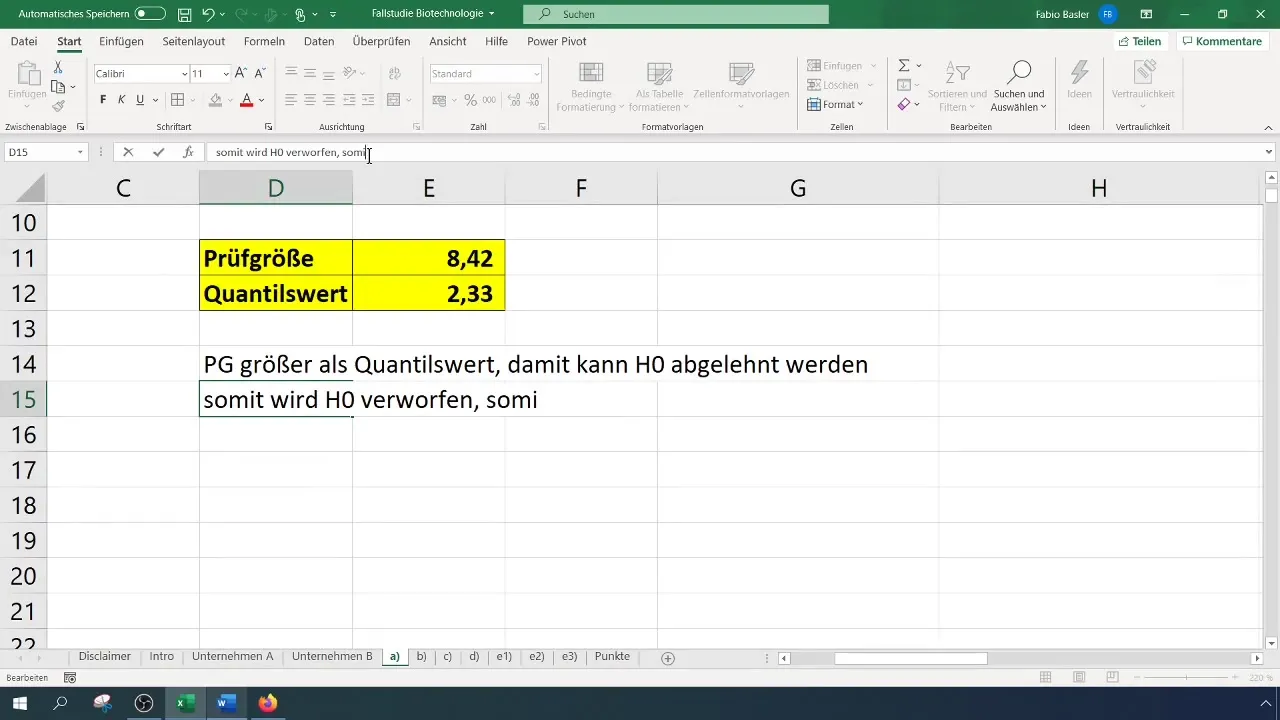
Mūsu gadījumā testa statistika ir 8,4, kas pārsniedz kritisko vērtību, kura ir 2,33. Tāpēc mēs varam noraidīt nulles hipotēzi. Tas norāda, ka panākumu rādītājs ir ievērojami uzlabojies.

Rezultātu interpretācija

Kad esat veicis testu un ieguvis rezultātus, jums tie jāinterpretē skaidrā kontekstā. Nulles hipotēzes noraidīšana nozīmē, ka jaunā pārbaudītā vērtība būtiski atšķiras no iepriekšējās, šajā gadījumā 59 %.

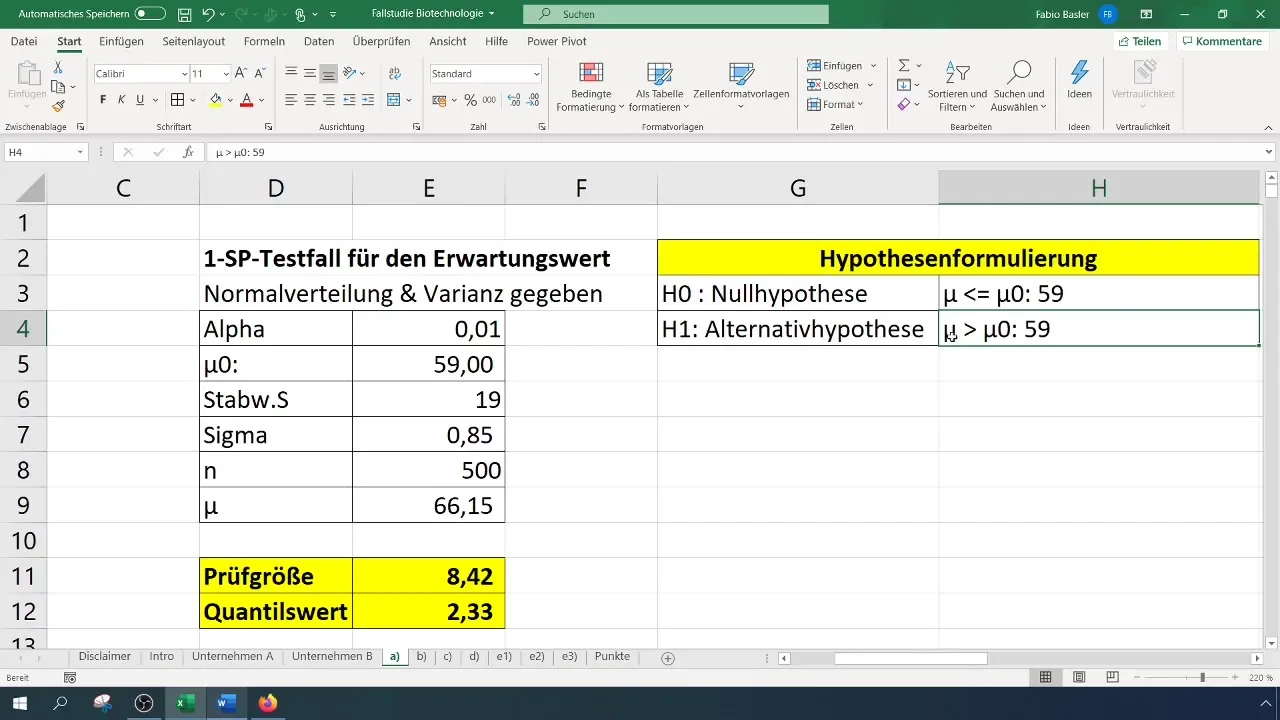
Šī informācija ir ārkārtīgi svarīga stratēģisko lēmumu pieņemšanai jūsu organizācijā. Tā apstiprina, ka centieni uzlabot sekmju rādītāju ir bijuši efektīvi.

Kopsavilkums

Šajā pamācībā jūs uzzinājāt, kā Excel programmā veikt 1-SP testu paredzamajai vērtībai. Izmantojot gadījuma izpēti, jūs varējāt sekot līdzi soļiem no hipotēžu izvirzīšanas līdz datu aprēķināšanai un rezultātu interpretēšanai. Šīs zināšanas ir vērtīgas ne tikai zinātniskai analīzei, bet arī praktiskai lietošanai uzņēmumā.