Divu paraugu t-tests ir būtisks instruments statistikā, ja vēlaties analizēt divu vidējo vērtību starpību. Šajā pamācībā uzzināsiet, kā šo testu viegli un efektīvi veikt programmā Excel. Izmantojot piemēru no biotehnoloģijas, uzzināsiet, kā salīdzināt un statistiski analizēt divu konkurējošu uzņēmumu veiksmes rādītājus.
Galvenie rezultāti
- Divu paraugu t-testa izmantošana, lai analizētu starpību starp diviem vidējiem rādītājiem.
- Hipotēžu formulēšana un pārbaude.
- Excel izmantošana rezultātu aprēķināšanai un vizualizēšanai.
Soli pa solim
Vispirms mēs sāksim ar nepieciešamo datu sagatavošanu un testa veikšanu programmā Excel.
Solis Nr. 1: Datu sagatavošana
Sāciet ar izejas datu apkopošanu par abu uzņēmumu veiksmes rādītājiem. Pieņemsim, ka jums ir dati no A un B uzņēmuma. Jums ir 100 datu kopu izlase no katra uzņēmuma.

Solis Nr. 2: Aprēķiniet izlases lielumu un vidējās vērtības
Izveidojiet tabulu programmā Excel, lai salīdzinātu izlases un to vidējās vērtības. Vispirms aprēķiniet abu uzņēmumu izlases lielumu (N) un vidējo vērtību (X).

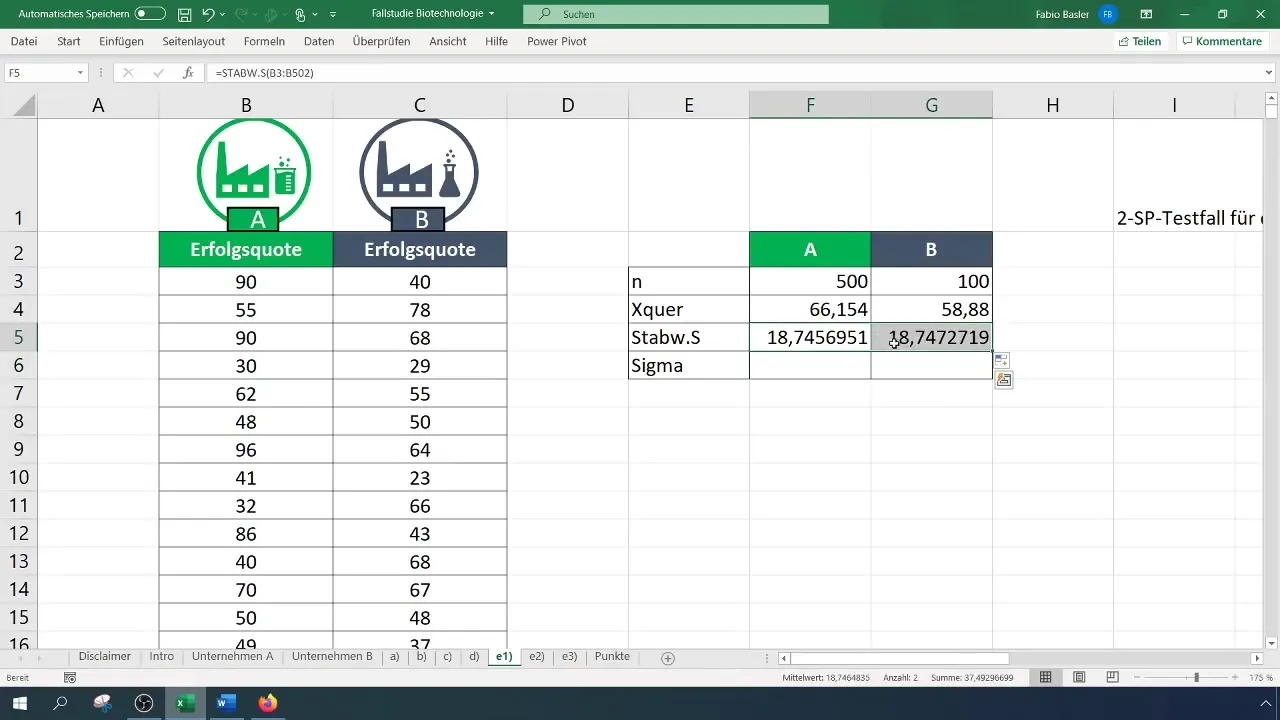
Solis Nr. 3: Nosakiet standartnovirzes
Aprēķiniet abu uzņēmumu standartnovirzi. Šīs vērtības ir svarīgas, lai aprēķinātu dispersiju un turpmākos aprēķinus.
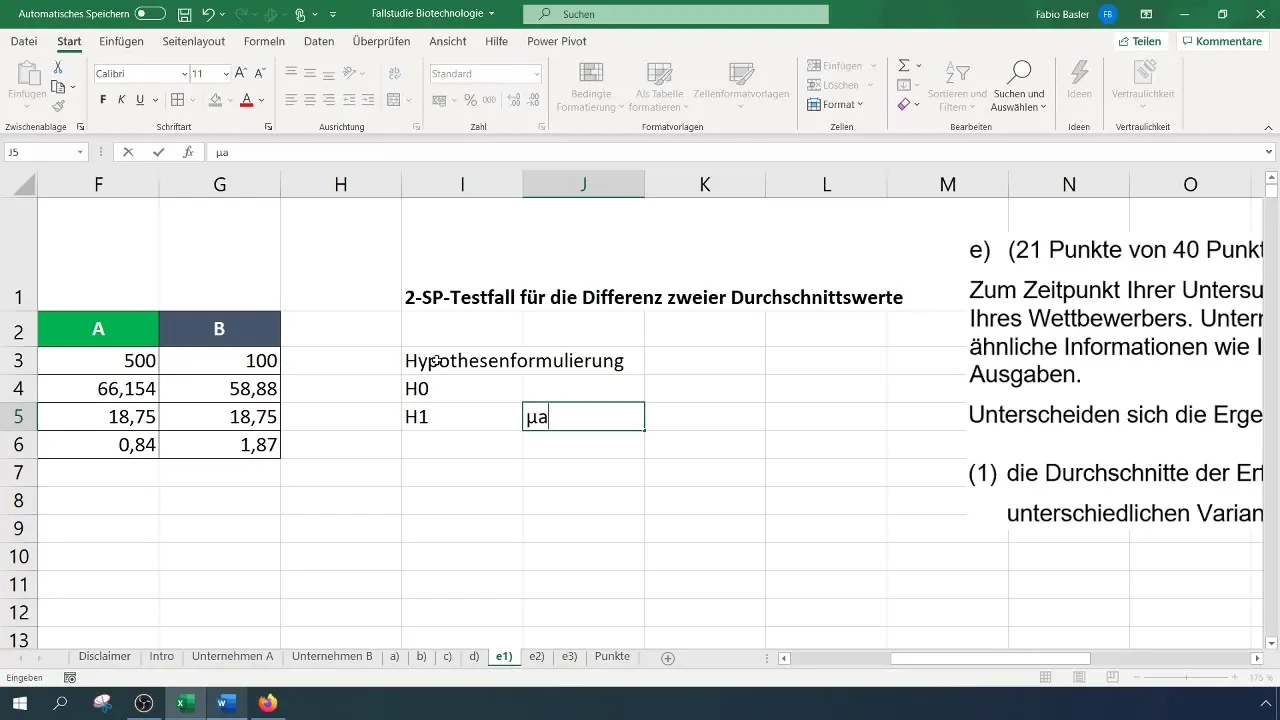
posms: Izvirziet hipotēzes
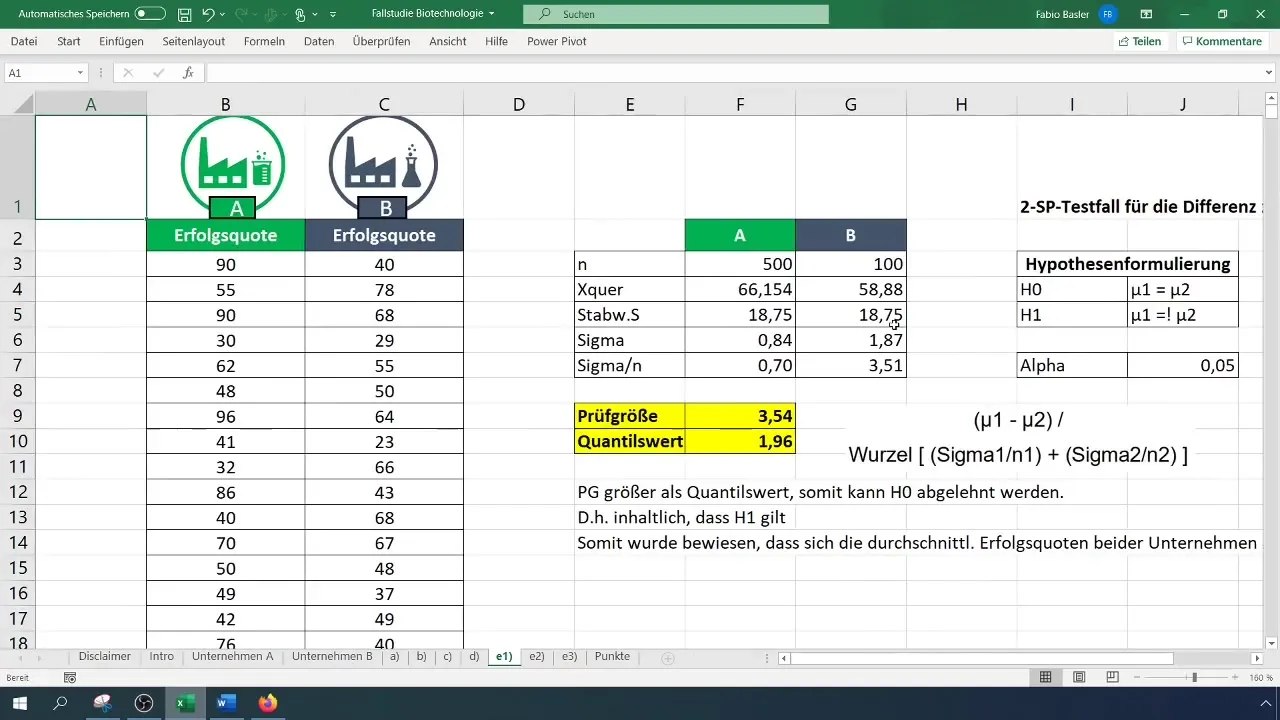
Izvirza nulles hipotēzi (H_0): Uzņēmumu A un B vidējās veiksmes rādītāju vērtības ir vienādas. Alternatīvā hipotēze (H_1): Vidējās veiksmes rādītāju vērtības ir atšķirīgas.
posms: Aprēķiniet testa mainīgo
Lai aprēķinātu testa statistiku, izmantojiet t-testa formulu. Aprēķiniet vidējo vērtību starpību un daliet to ar kvadrātsakni no katras izlases variāciju summas.
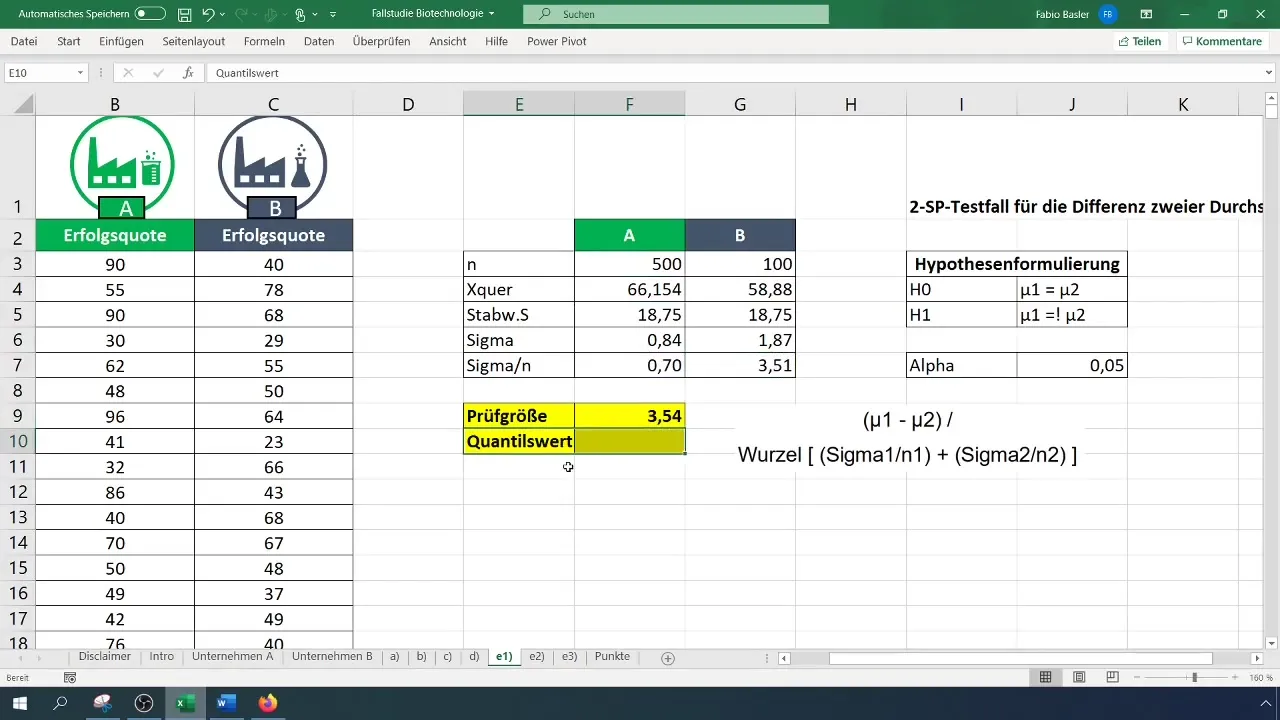
Solis 6: Noteikt kritisko vērtību
Lai noteiktu kritisko vērtību, izmantojiet divpusējo t sadalījumu. Iestatiet alfa līmeni 0,05. Pārbaudiet t sadalījuma tabulu vai aprēķiniet koeficientu tieši programmā Excel.
Solis 7: Izlemiet hipotēzi
Salīdziniet aprēķināto testa statistiku ar kritisko vērtību. Ja testa statistika ir lielāka par kritisko vērtību, noraidiet nulles hipotēzi (H_0) un tādējādi apstipriniet alternatīvo hipotēzi (H_1).
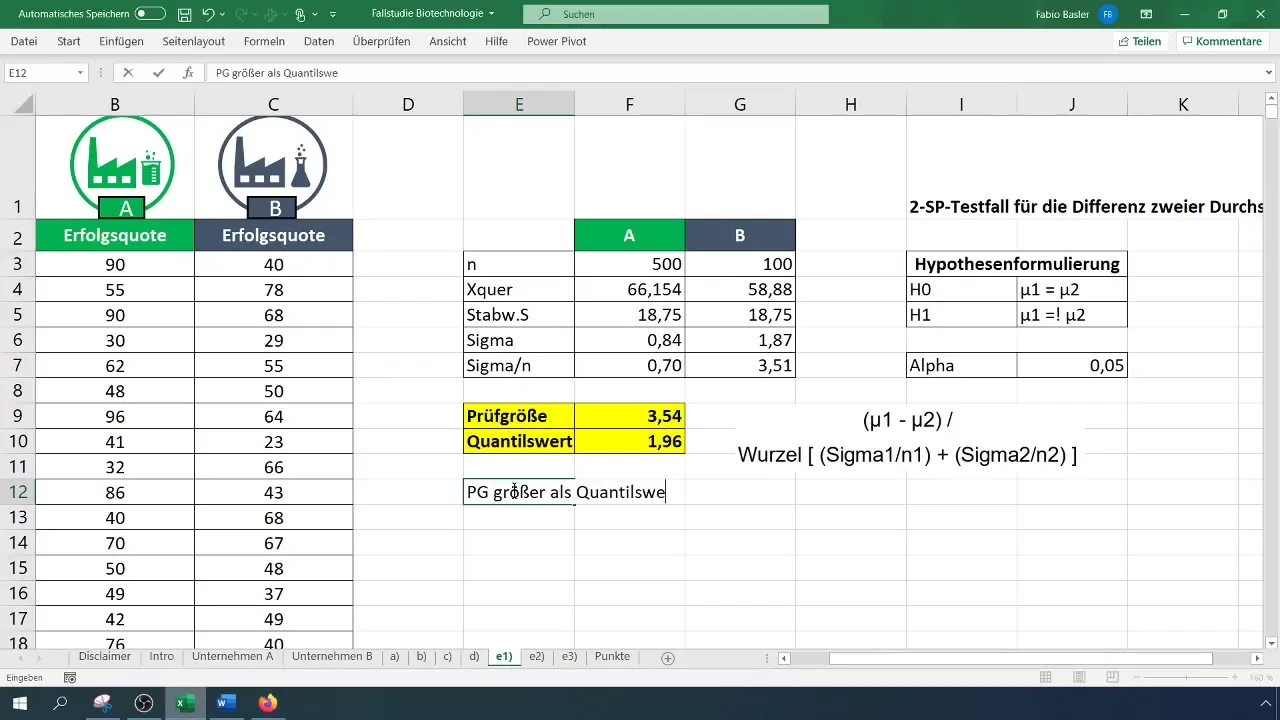
posms: Rezultātu interpretācija
Visbeidzot, interpretējiet rezultātu. Šajā piemērā tika konstatēts, ka abu uzņēmumu vidējie panākumu rādītāji būtiski atšķiras.
Kopsavilkums
Jūs esat iemācījušies, kā Excel programmā veikt divu paraugu t-testu, lai pārbaudītu divu grupu vidējo vērtību atšķirības. Lai pieņemtu pamatotus un uz informāciju balstītus lēmumus, ir svarīgi veikt visus posmus no datu sagatavošanas līdz hipotēžu formulēšanai un rezultātu interpretēšanai.
Biežāk uzdotie jautājumi
Kas ir divu paraugu t-tests? Divu paraugu t-tests salīdzina divu grupu vidējās vērtības, lai noteiktu, vai tās būtiski atšķiras.
Kā formulēt hipotēzes? Nulles hipotēze (H_0) nosaka, ka vidējie lielumi ir vienādi, bet alternatīvā hipotēze (H_1) nosaka, ka tie ir atšķirīgi.
Kā aprēķināt testa statistiku? Testa statistiku aprēķina, vidējo vērtību starpību dalot ar variāciju summas kvadrātsakni.
Ko man darīt pēc aprēķina? Salīdziniet testa statistiku ar kritisko vērtību, lai izlemtu, vai varat noraidīt nulles hipotēzi.
Kāpēc standartnovirze ir svarīga?Standartnovirze palīdz izprast datu mainību, kas ir ļoti svarīga testa statistikas aprēķināšanai.


