Chi-kvadrāta atbilstības atbilstības tests ir vienkārša metode, lai pārbaudītu hipotēzi, ka attiecīgajai datu sērijai ir normāls sadalījums. Šajā rokasgrāmatā uzzināsiet, kā Excel programmā veikt chi-kvadrāts testu, lai noteiktu, vai viedtālruņu pārdošanas rezultāti atbilst normālajam sadalījumam. Mēs soli pa solim izstaigāsim šo procesu, sākot no klasificētas biežumu tabulas izveides līdz testa statistikas aprēķināšanai un salīdzināšanai ar chi-kvadrāta kritisko vērtību.
Galvenie secinājumi
- Chi-kvadrāta atbilstības atbilstības tests palīdz pārbaudīt normālu sadalījumu.
- Ir svarīgi izveidot klasificētu biežumu tabulu.
- Testa statistiku salīdzina ar kritisko vērtību, lai noraidītu vai pieņemtu nulles hipotēzi.
Soli pa solim
Solis Nr. 1: Sagatavojiet datus
Lai veiktu chi-kvadrāts testu, vispirms ir nepieciešami dati. Pārkopējiet viedtālruņu pārdošanas datus Excel izklājlapā. Pārliecinieties, ka dati ir sakārtoti vienā slejā.

Solis Nr. 2: Izveidojiet histogrammu
Lai iegūtu sākotnēju vizuālu priekšstatu par sadalījumu, izveidojiet savu datu histogrammu. Lai to izdarītu, dodieties uz "Insert" un izvēlieties "Charts". Pievienojiet histogrammu, izvēloties datu diapazonu.
Solis Nr. 3: Izveidojiet klasificētu biežumu tabulu
Jums ir nepieciešama klasificēta biežumu tabula chi-kvadrāta testam. Vispirms nosakiet tabulas klašu skaitu - šajā gadījumā mēs izmantosim sešas klases. Aprēķiniet intervālu platumu un attiecīgi izveidojiet tabulu.
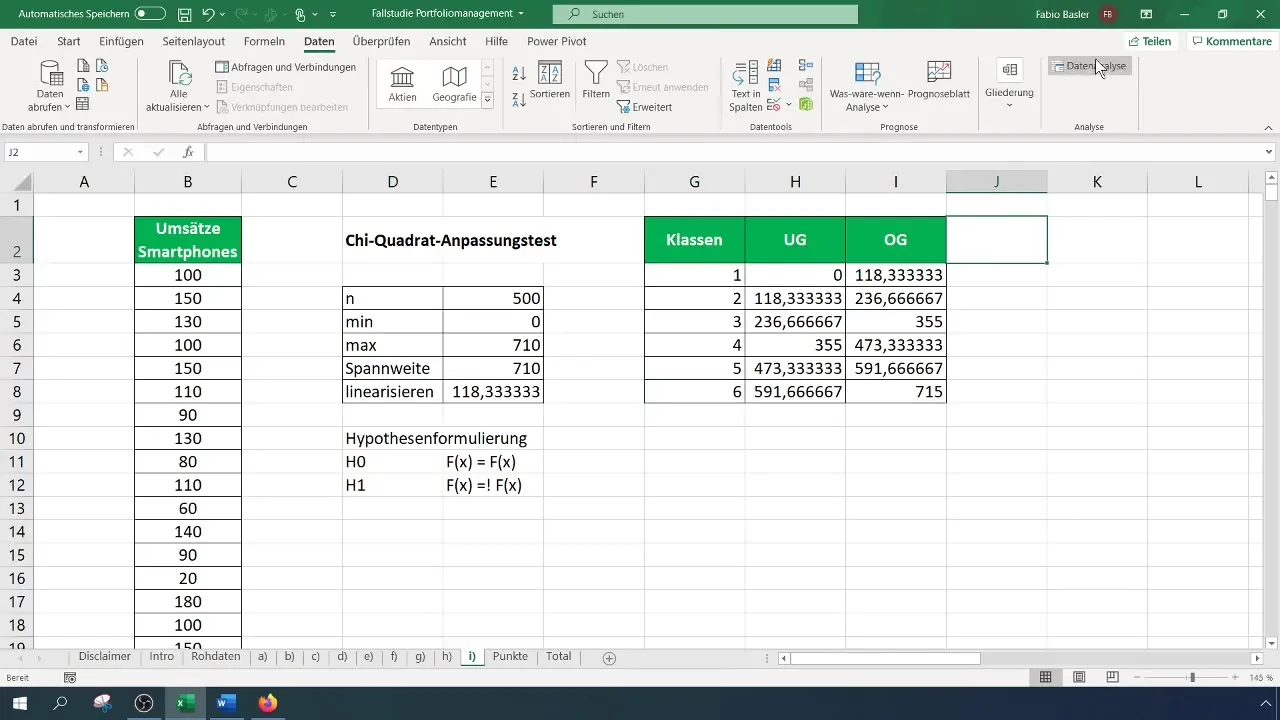
Solis Nr. 4: Aprēķiniet frekvences
Tagad jāaprēķina novērotās frekvences katrai klasei. Izvēlnē dodieties uz "Datu analīze" un izvēlieties "Histogramma". Izvēlieties datu ievades intervālu un klašu robežas. Nosakiet biežumu tabulas izejas diapazonu.
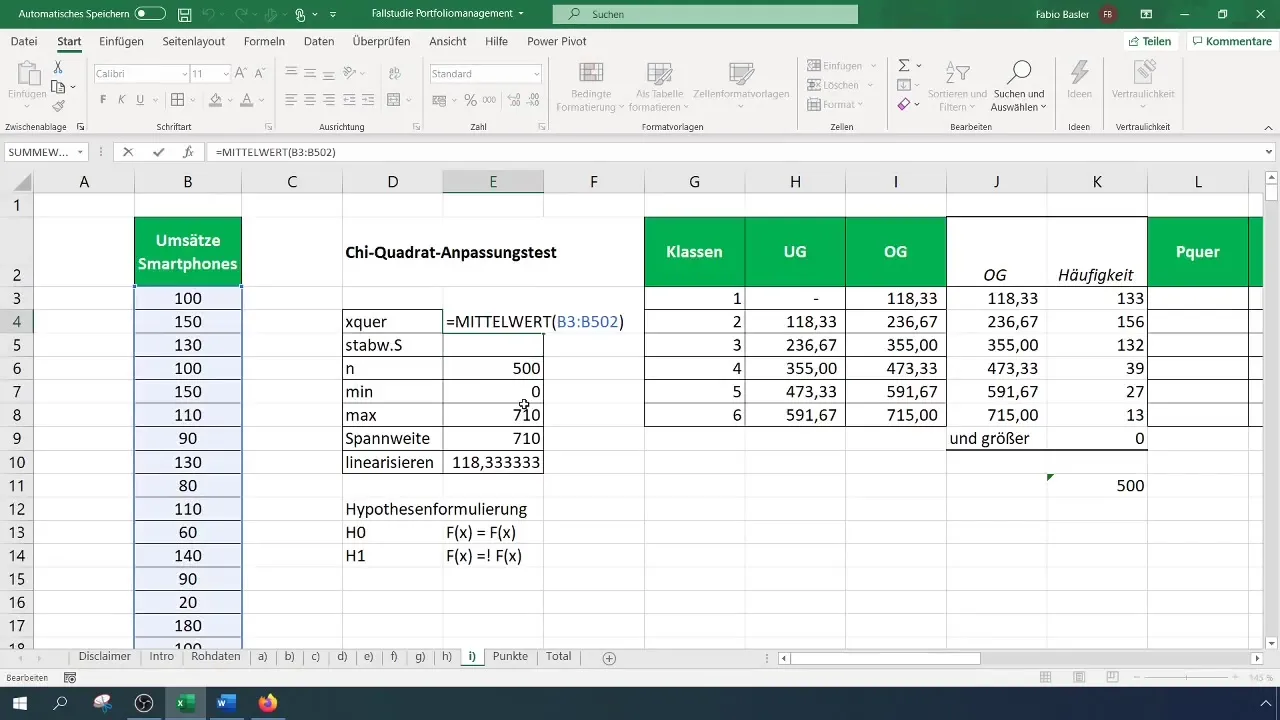
Solis Nr. 5: Aprēķiniet sagaidāmās frekvences
Lai noteiktu sagaidāmās frekvences, aprēķiniet katras klases varbūtības, pamatojoties uz pieņemto normālo sadalījumu. Lai to izdarītu, jums ir nepieciešams jūsu datu vidējais lielums un standartnovirze.
Solis Nr. 6: Aprēķināt testa statistiku
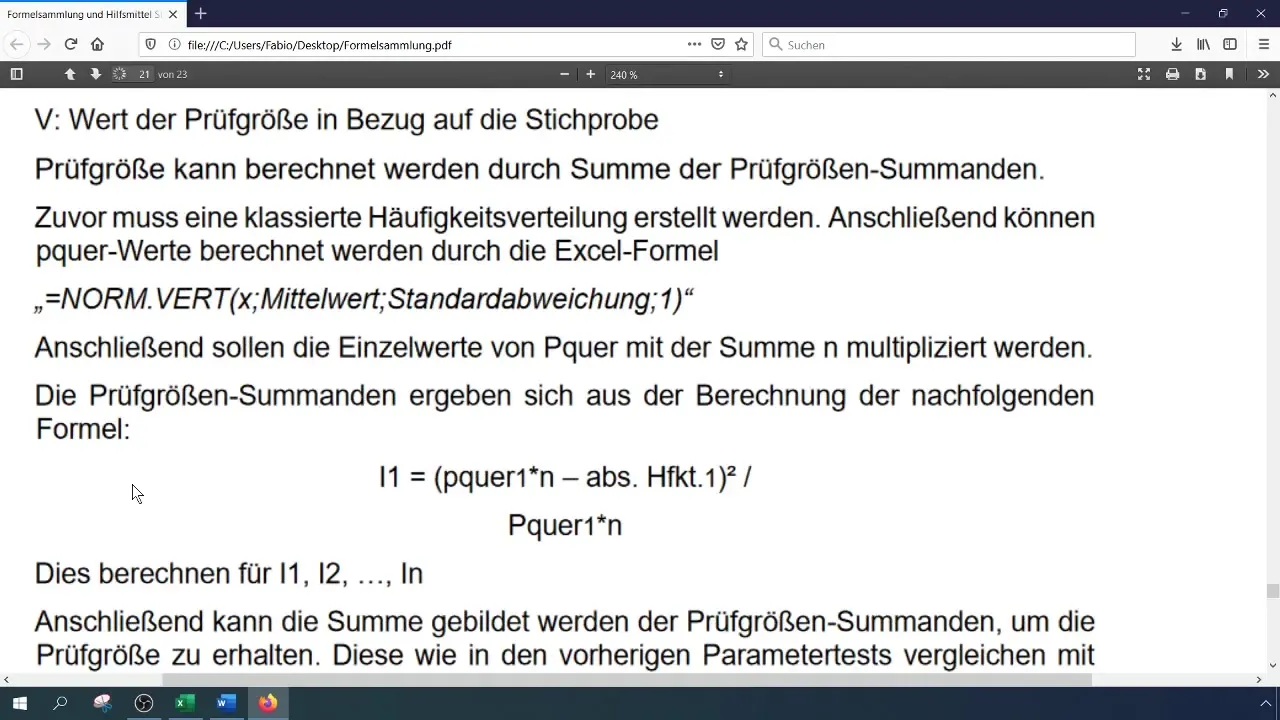
Aprēķiniet testa statistiku (chi-kvadrāts), izmantojot formulu
[ \chi^2 = \sum \frac{(O_i - E_i)^2}{E_i} ] ]
kur (O_i) ir novērotās un (E_i) paredzamās frekvences. Šo aprēķinu var veikt Excel programmā, saglabājot atsevišķas sastāvdaļas atsevišķās šūnās.
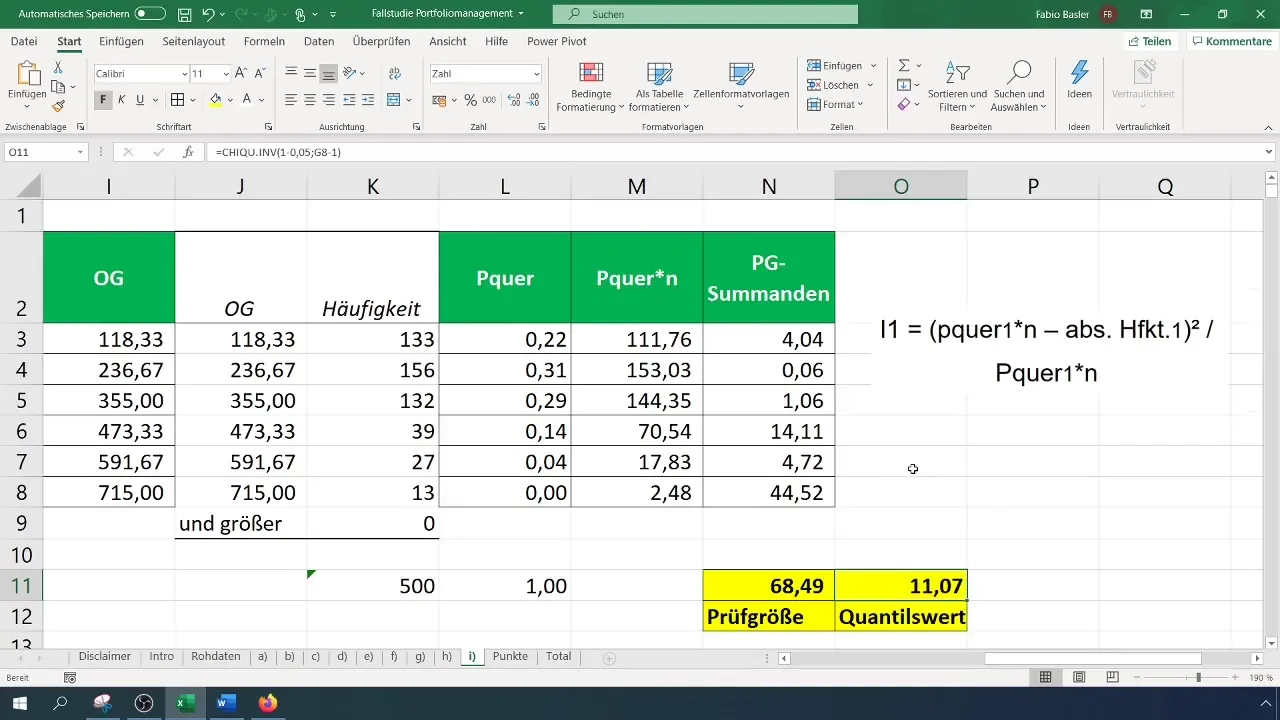
posms: Aprēķināt kritisko vērtību
Lai novērtētu testa statistiku, ir jāaprēķina kritiskā vērtība ( \chi^2 ) jūsu ticamības līmenim un brīvības pakāpju skaitam. Brīvības pakāpju skaits chi-kvadrāta testam ir (k - 1), kur (k) ir klašu skaits.
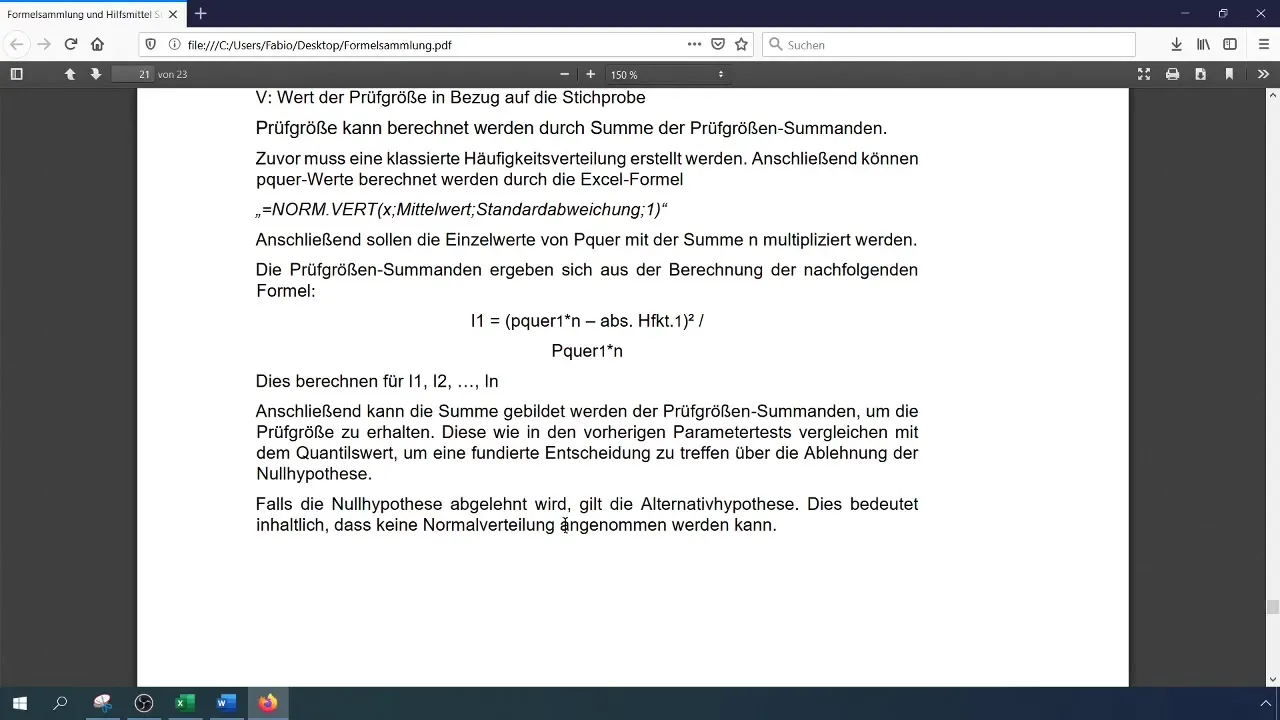
Solis 8: Pārbaudiet hipotēzes
Salīdziniet aprēķināto testa statistiku ar kritisko vērtību. Ja testa statistika ir lielāka par kritisko vērtību, noraidiet nulles hipotēzi, kas nozīmē, ka dati nav sadalīti normāli. Pretējā gadījumā pieņemiet nulles hipotēzi.
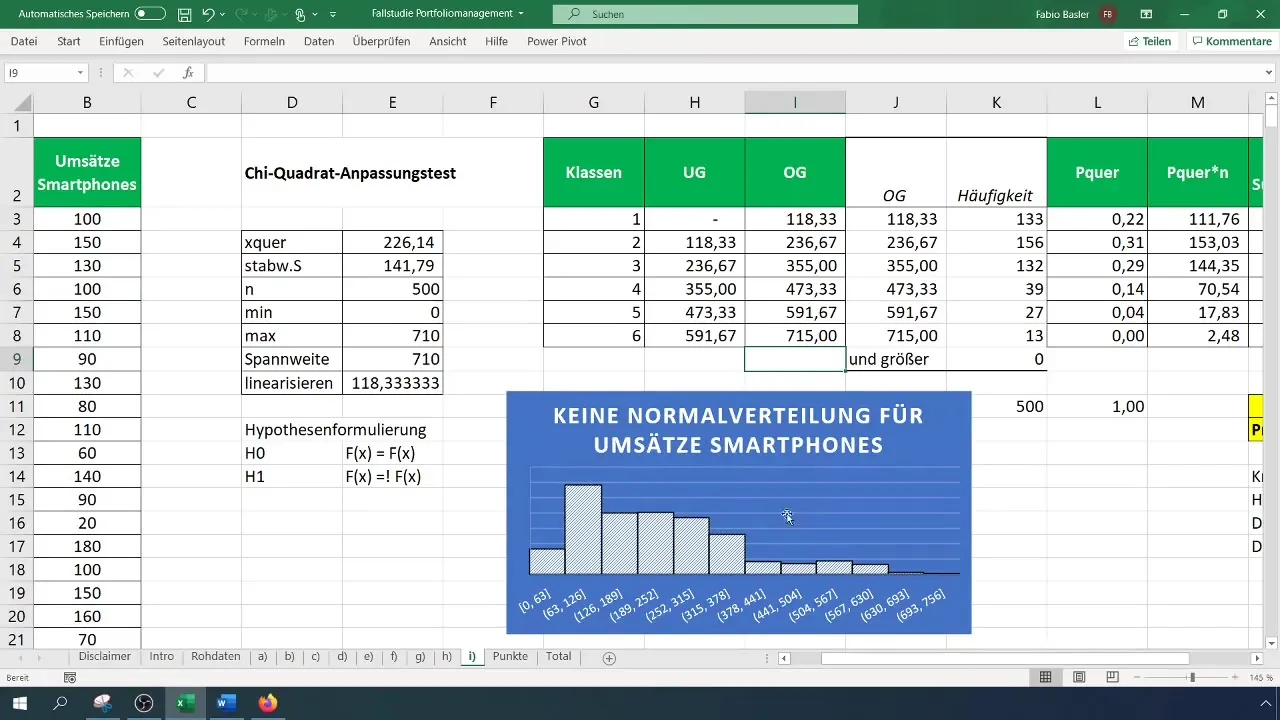
posms: Apkopojiet rezultātus
Ierakstiet savus rezultātus un paplašiniet tos, iekļaujot grafiskos datus un hipotēžu testus. Neaizmirstiet pārbaudīt savu histogrammu, lai vizuāli apstiprinātu, ka sadalījums nav normāls.
Apkopojums
Šajā rokasgrāmatā esat iemācījušies, kā Excel programmā veikt Chi-Square atbilstības testu, lai analizētu viedtālruņu pārdošanas apjomu normālo sadalījumu. Šie soļi ietver klasificēto biežumu tabulas izveidi, sagaidāmo biežumu aprēķinus, testa statistiku un visbeidzot tās salīdzināšanu ar kritisko vērtību.
Biežāk uzdotie jautājumi
Kas ir chi-kvadrāta atbilstības tests?Chi-kvadrāta atbilstības tests pārbauda, vai novērotais frekvenču sadalījums atbilst normālajam sadalījumam.
Cik klases ir vajadzīgas biežumu tabulai? Lai datus varētu jēgpilni analizēt, parasti ir lietderīgas vismaz 5 līdz 10 klases.
Ko darīt, ja nulles hipotēze tiek noraidīta? Ja nulles hipotēze tiek noraidīta, tas nozīmē, ka dati nav sadalīti normāli.
Kā aprēķināt kritisko chi-kvadrāta vērtību?Kritisko vērtību nolasa no chi-kvadrāta sadalījuma tabulas, izmantojot brīvības pakāpes un vēlamo nozīmīguma līmeni.


