Lai gūtu panākumus uzņēmējdarbībā un pārdošanā, ir svarīgi prast izmantot datu analīzes rīkus programmā Excel. Šajā rokasgrāmatā galvenā uzmanība pievērsta korelācijas un regresijas analīzei , lai noskaidrotu, kā darbinieku skaits un tālruņa zvanu skaits ietekmē pārdošanas rādītājus. Abu analīžu veikšana palīdzēs jums kvantitatīvi novērtēt šīs sakarības un padarīs saprotamu rezultātu interpretāciju.
Galvenie secinājumi
- Atšķirība starp korelāciju un regresiju: korelācija parāda saistību starp diviem mainīgajiem lielumiem, savukārt regresija analizē vairāku neatkarīgo mainīgo ietekmi uz atkarīgo mainīgo.
- Ieskats modeļa statistiskajā nozīmībā un kvalitātē.
- Kvantitatīvs regresoru nozīmes novērtējums.
Soli pa solim
1. Sagatavošanās datu analīzei
Pirms analīzes uzsākšanas ir jāpārliecinās, ka dati ir pareizi sagatavoti programmā Excel. Importējiet datus par pārdošanas apjomiem, darbinieku skaitu un tālruņa zvaniem Excel darblapā. Pārbaudiet, vai visas datu kopas ir pilnīgas un vai ir pieejami nepieciešamie mainīgie lielumi.

2 Veiciet korelācijas analīzi
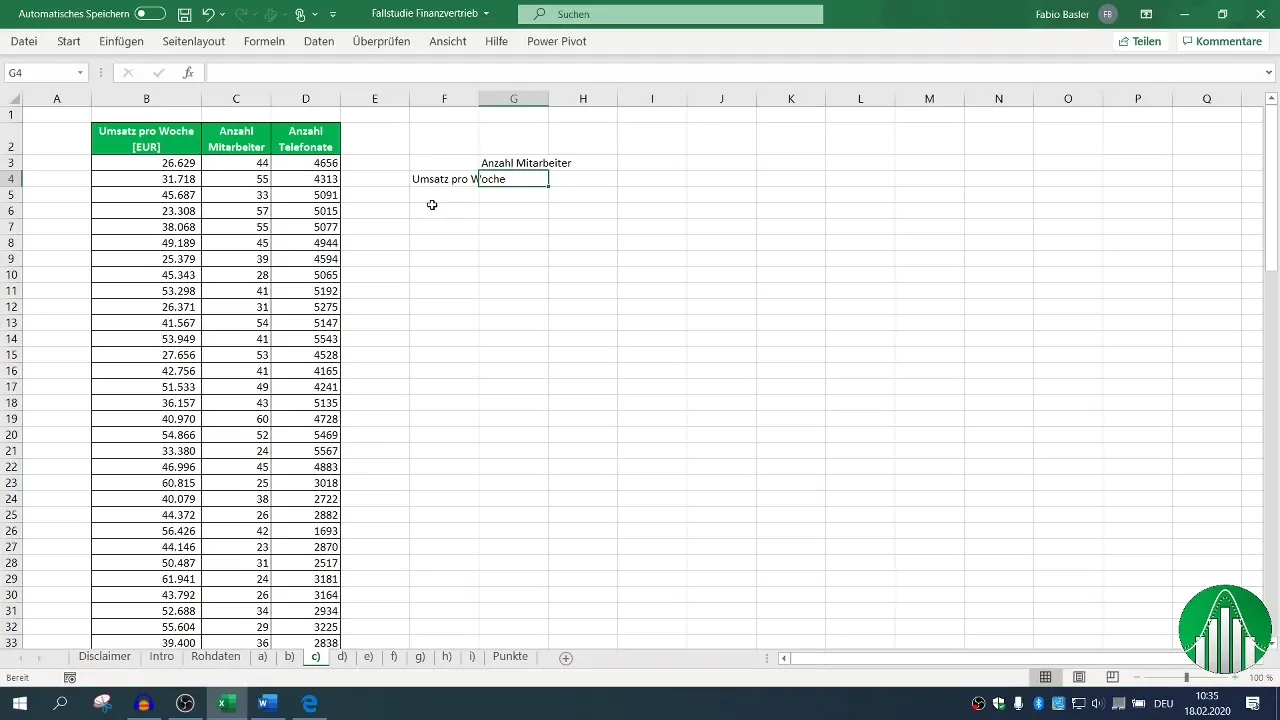
Lai analizētu korelāciju starp mainīgajiem lielumiem apgrozījums, darbinieki un tālruņa zvani, varat aprēķināt korelācijas koeficientu. Lai to izdarītu, programmā Excel izmantojiet formulu =CORREL(). Lai iegūtu pārskatu par visiem mainīgajiem, izveidojiet korelācijas matricu.
Vispirms atlasiet atbilstošās kolonnas apgrozījumam un darbinieku skaitam. Izmantojiet formulu =CORREL(, lai atlasītu apgrozījuma un darbinieku skaita diapazonus. Rezultāts parāda, cik spēcīga ir korelācija.
3. Korelācijas matricas izveide
Lai veiktu visaptverošāku analīzi, iesakām izmantot Excel datu analīzes funkcijas. Aktivizējiet datu analīzes funkciju, ja tas vēl nav izdarīts. Dodieties uz cilni "Dati", noklikšķiniet uz "Datu analīze" un izvēlieties "Korelācija".
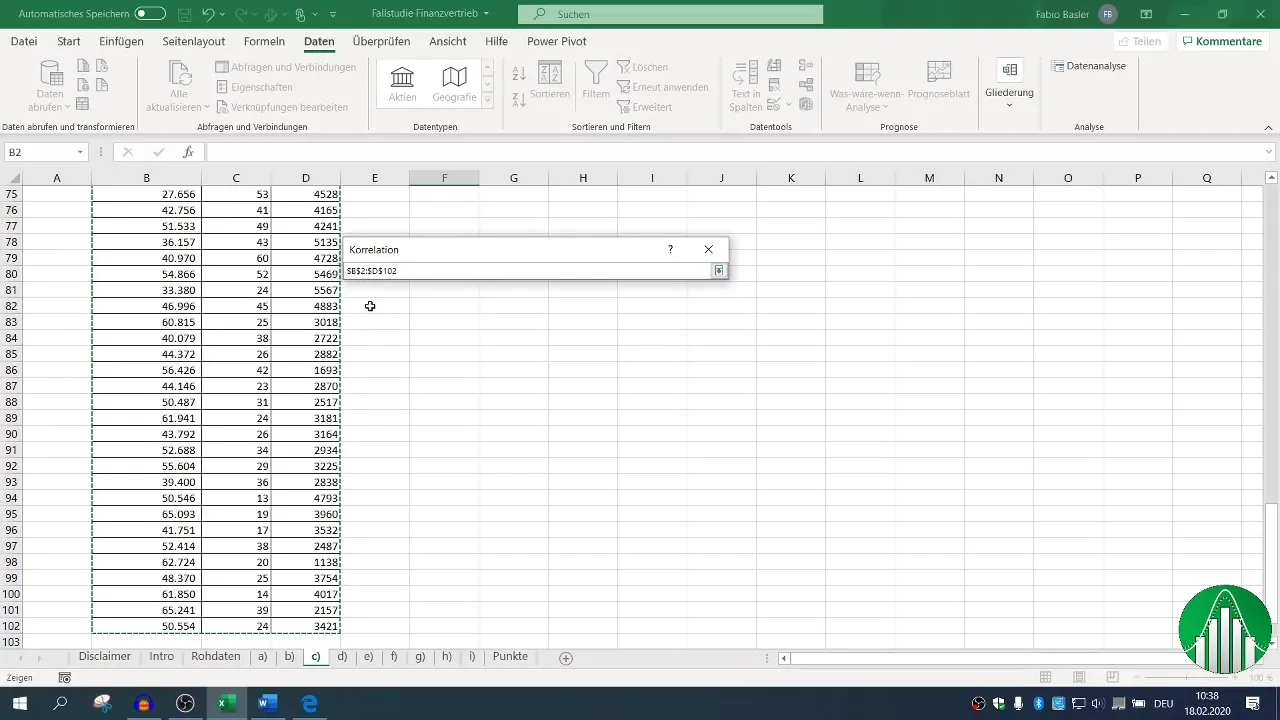
Definējiet datu ievades diapazonu un atzīmējiet izvēles rūtiņu virsrakstam, lai Excel pareizi atpazītu uzlīmes. Kad esat definējis izejas diapazonu, varat ģenerēt korelācijas matricu, kas parāda visas attiecīgās sakarības.
4. Korelāciju vizualizācija
Lai rezultātus padarītu skaidrākus, var būt noderīgs grafisks attēlojums, izmantojot XY diagrammu. Izvēlieties savus X un Y datus un ģenerējiet punktu mākoni.
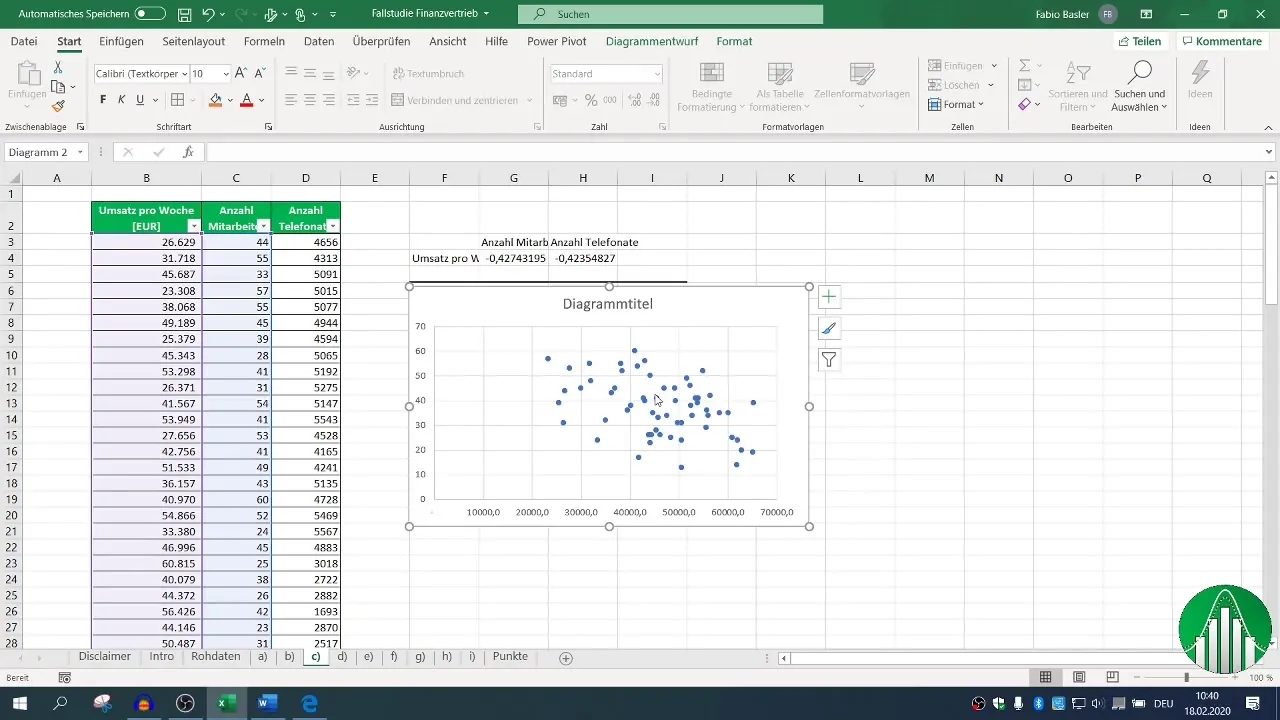
Pievienojiet tendences līniju, lai vizualizētu sakarības. Tas var sniegt intuitīvāku ieskatu datos.
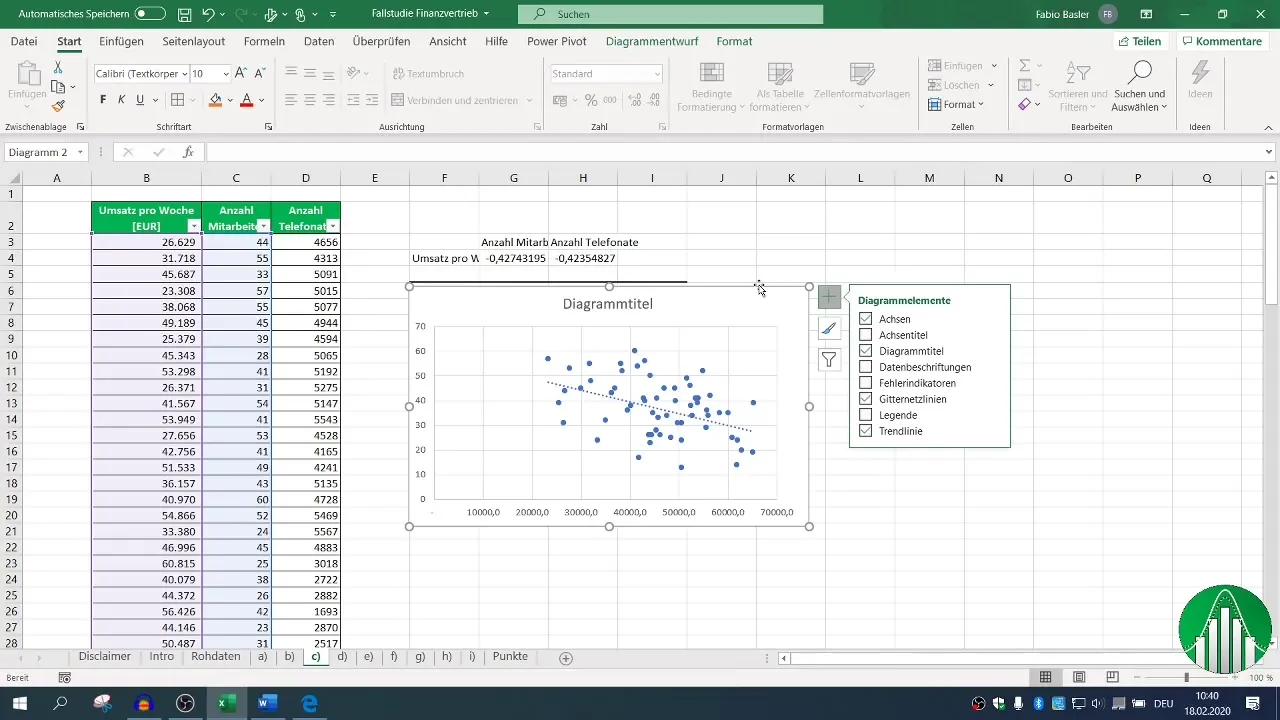
5. Regresijas analīzes veikšana
Tagad ir jāveic regresijas analīzes posms. Atkal atveriet sadaļu "Dati" un izvēlieties "Datu analīze", pēc tam "Regresija". Šeit varat definēt atkarīgo mainīgo (apgrozījums) un neatkarīgos mainīgos (darbinieku skaits un tālruņa zvani) ievades jomai.
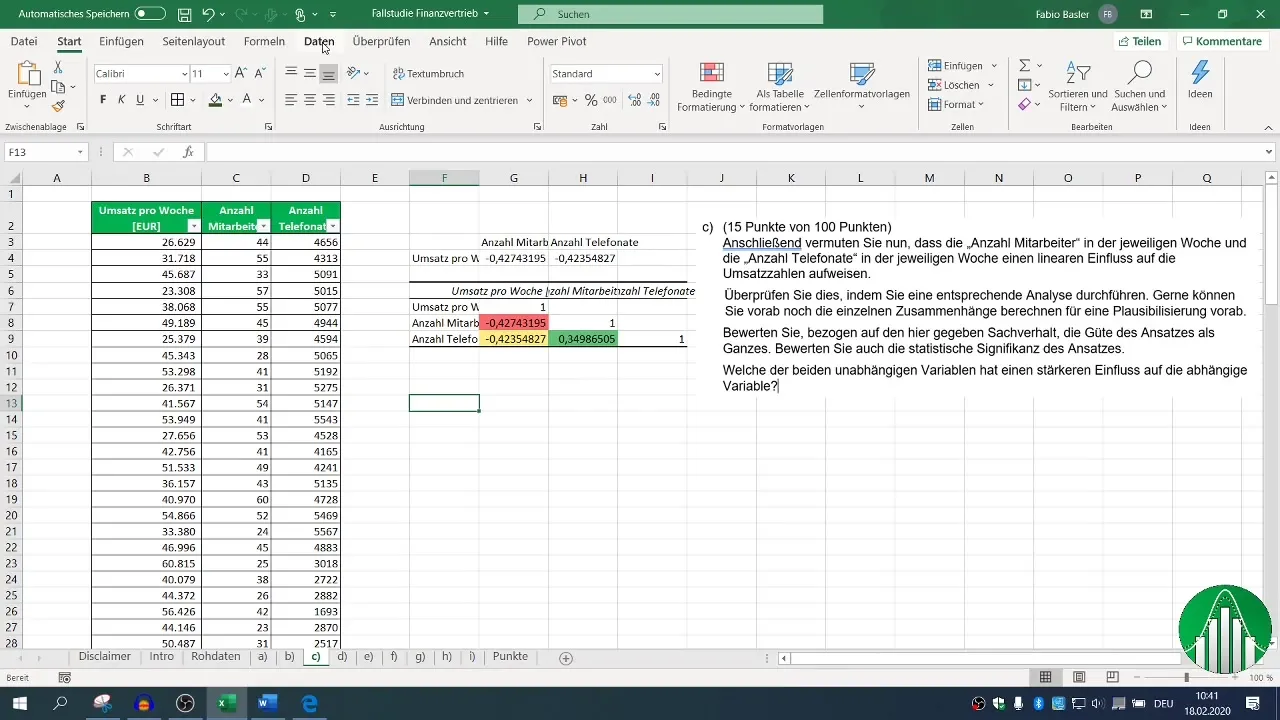
Pārliecinieties, ka ir iestatīta vērtību pozīcija, un definējiet savu izejas apgabalu. Pēc noklusējuma ir iestatīts 95 % ticamības līmenis, kas ir pietiekams lielākajai daļai analīžu.
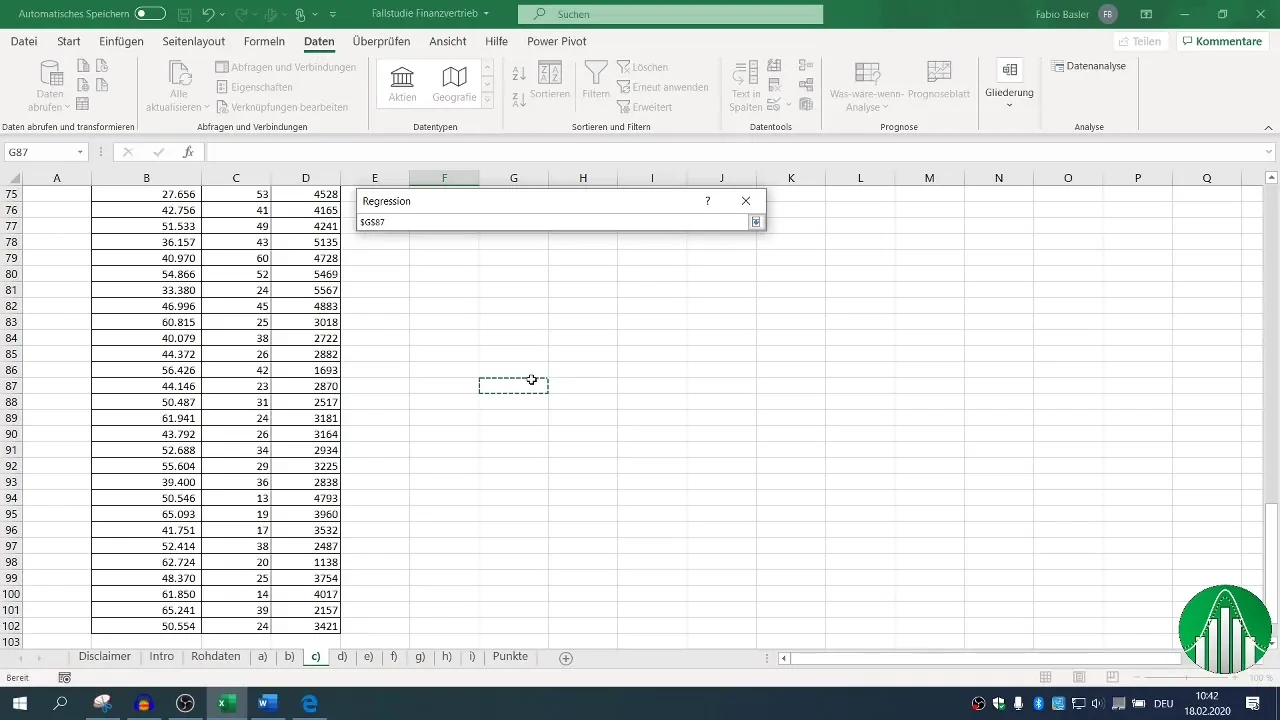
6. Regresijas analīzes novērtēšana
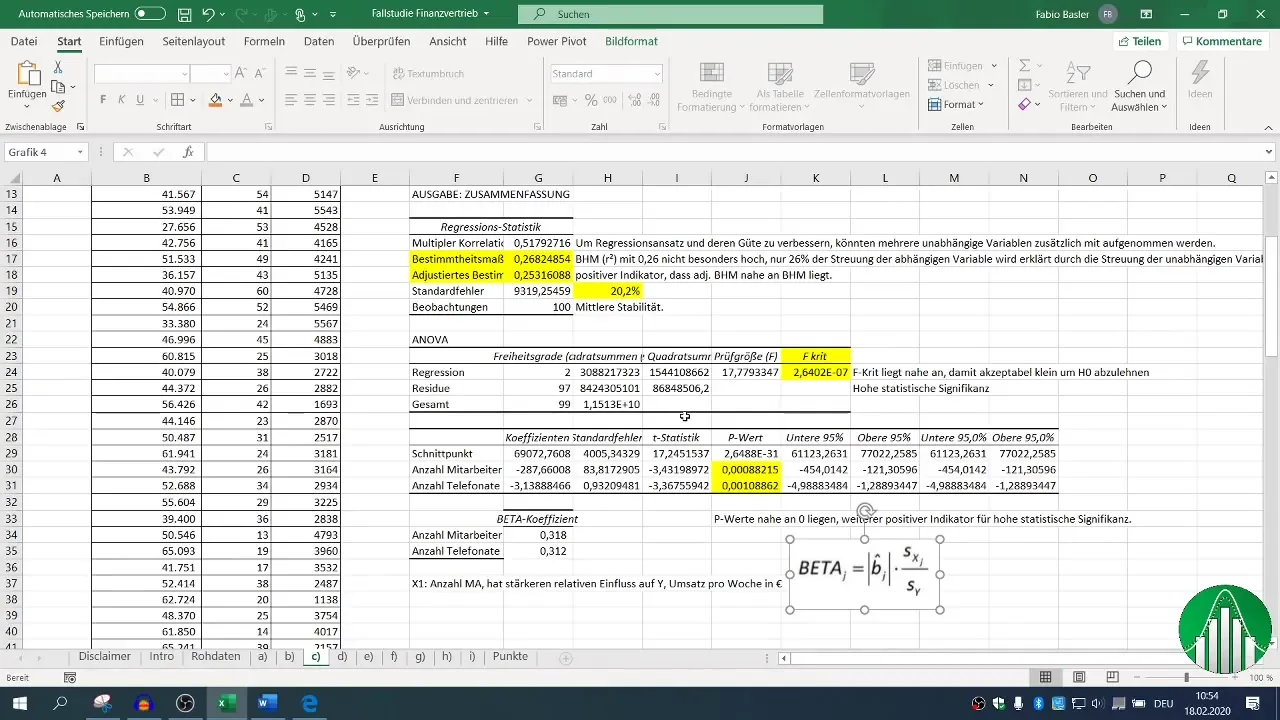
Kad regresija ir veikta, jūsu rīcībā ir dažādi izvades bloki. Koncentrējieties uz determinācijas koeficientu (R²), kas raksturo modeļa kvalitāti. R² 0,26 norāda, ka tikai 26 % no pārdošanas apjoma mainīguma izskaidro neatkarīgie mainīgie.
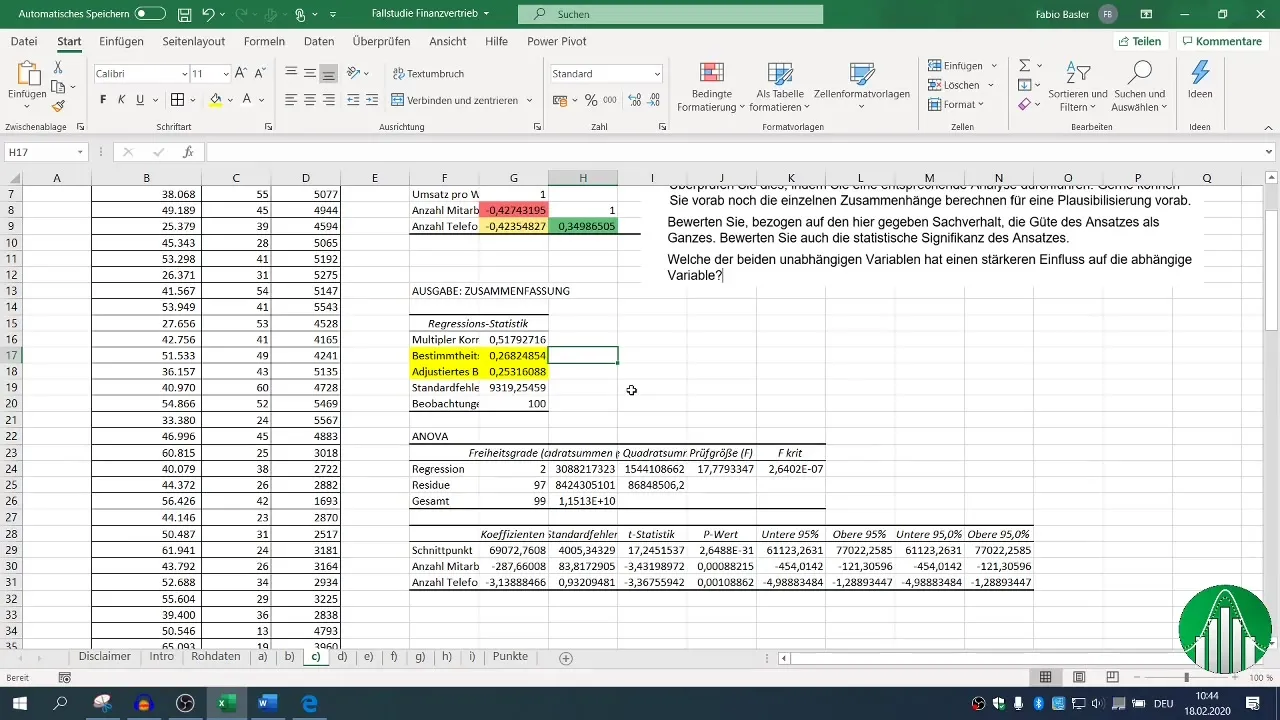
Koriģētajam determinācijas koeficientam jābūt tuvu R², kas šajā gadījumā ir pozitīvs rādītājs.
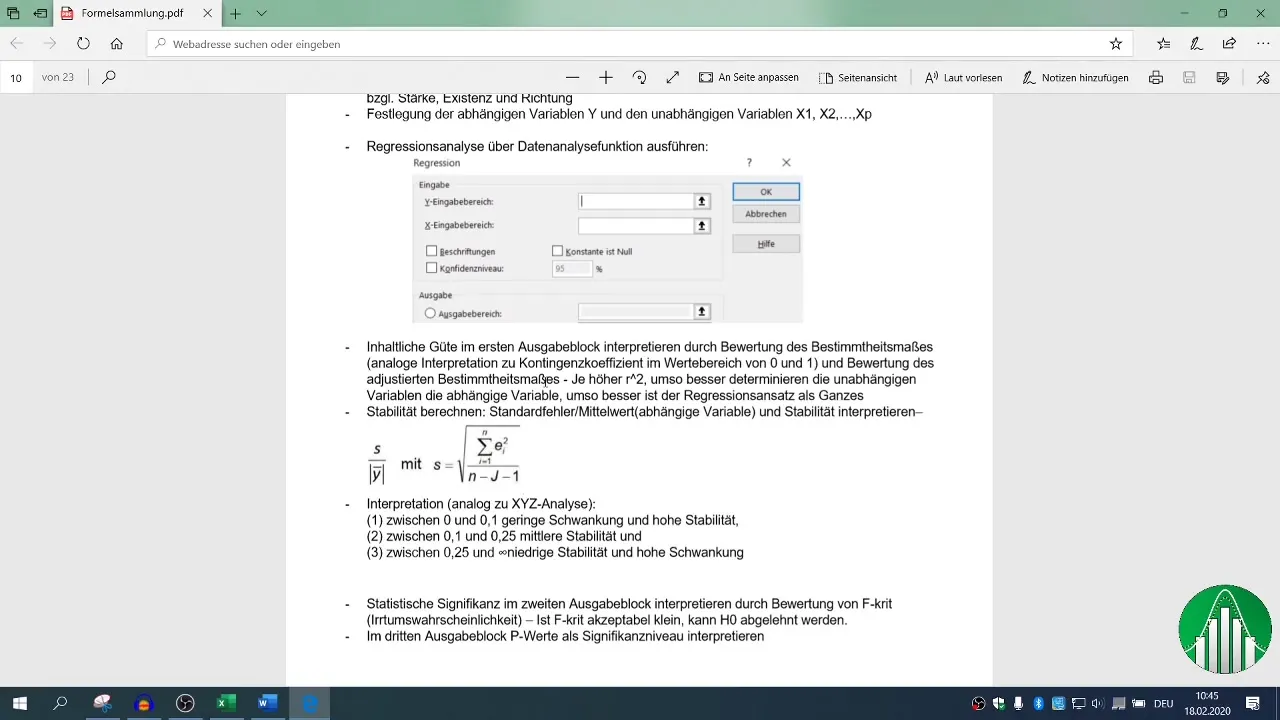
7 Novērtēt statistisko nozīmīgumu
Lai novērtētu jūsu modeļa statistisko nozīmīgumu, ļoti svarīga ir neatkarīgo mainīgo F vērtība un p-vērtība. Ja p vērtība ir mazāka par 0,05, tas norāda, ka sakarība ir statistiski nozīmīga.
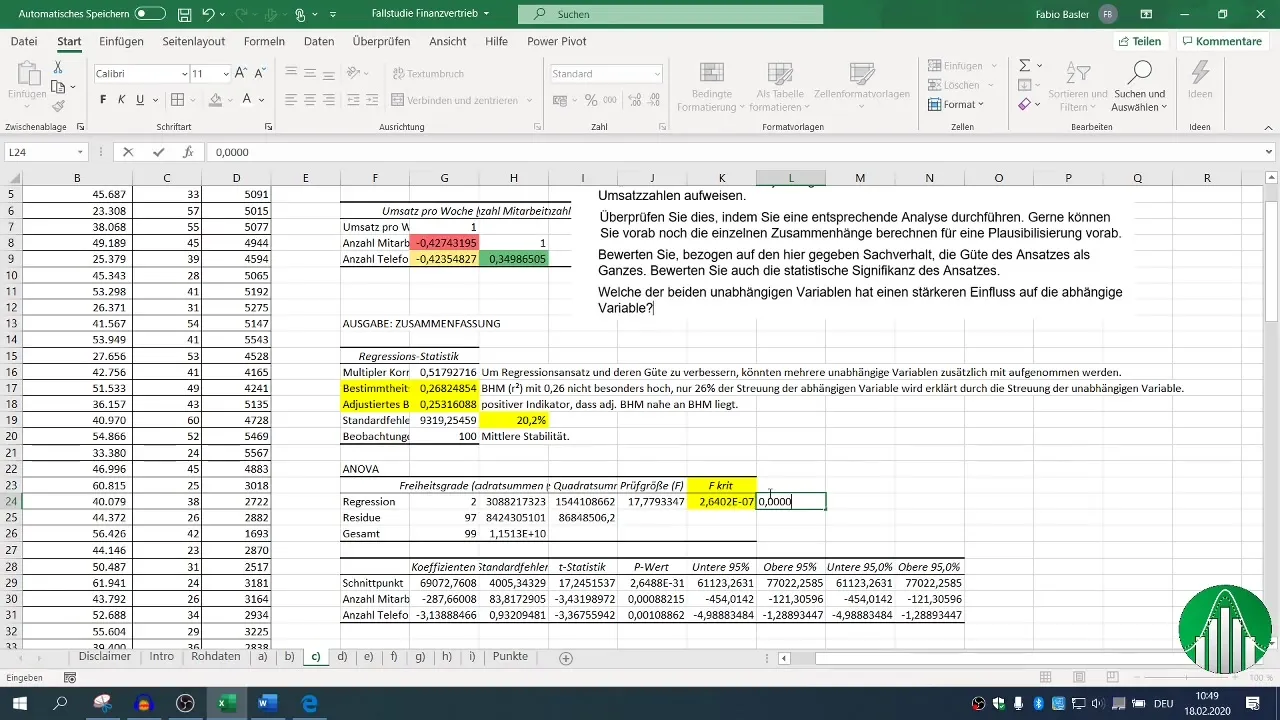
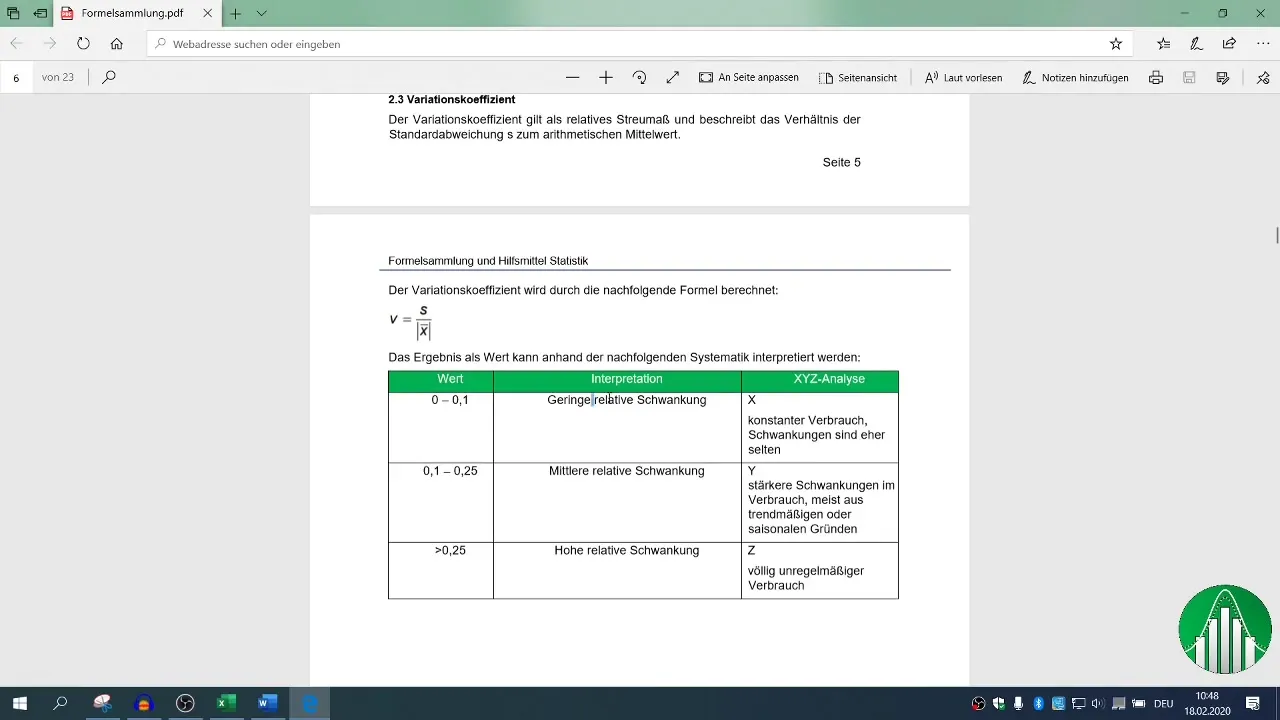
Šo statistisko parametru novērtēšana kopā ar R² palīdz jums saprast jūsu rezultātu stabilitāti un nozīmīgumu.
8 Ietekmējošo faktoru salīdzinājums
Galu galā jūs interesē, kuram faktoram - darbinieku skaitam vai telefona zvaniem - ir lielāka ietekme uz pārdošanas rādītājiem. Šajā gadījumā ņemiet beta koeficientus un salīdziniet tos.
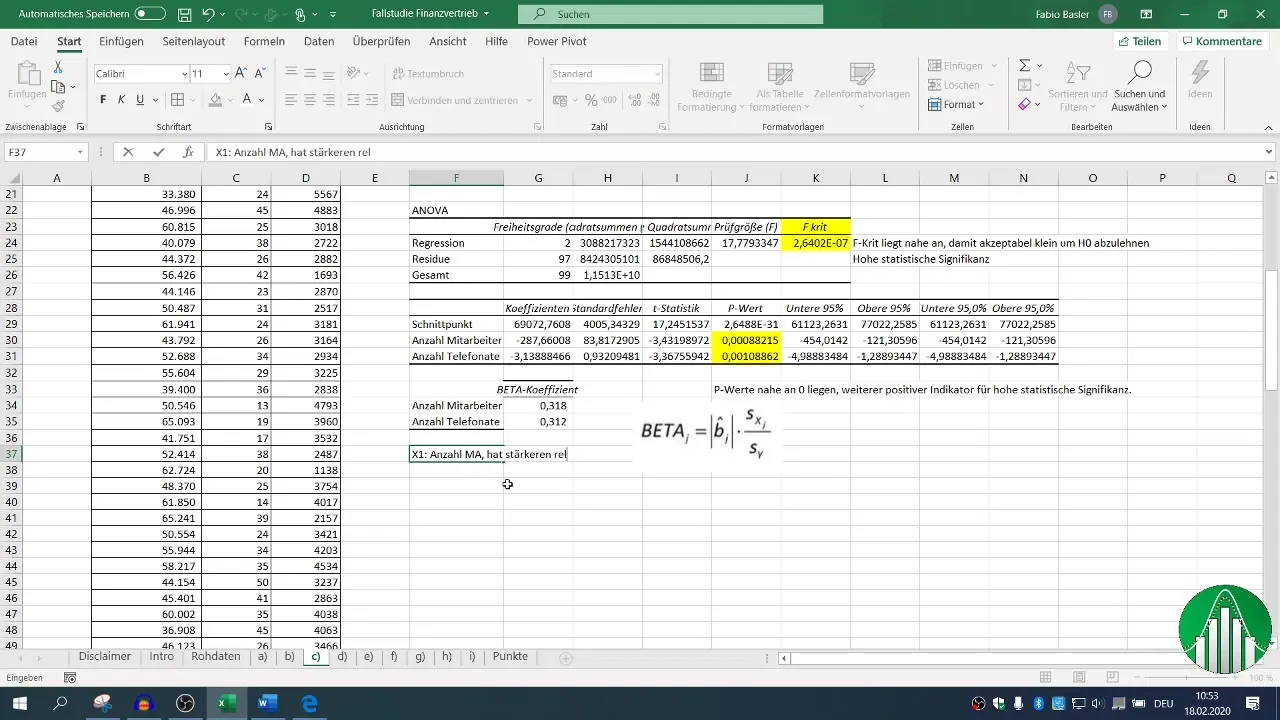
Lielāks beta koeficients norāda uz relatīvo ietekmi; var izrādīties, ka darbinieku skaitam ir lielāka ietekme uz apgrozījumu nekā telefona zvanu skaitam.
Kopsavilkums
Iepriekšējā analīze ir sniegusi vērtīgu ieskatu par statistiskajām attiecībām starp mainīgajiem lielumiem apgrozījums, darbinieku skaits un tālruņa zvani. Sistemātiski veicot korelācijas un regresijas analīzi programmā Excel, jūs varat pieņemt pamatotus lēmumus, pamatojoties uz iegūtajiem rezultātiem.
Biežāk uzdotie jautājumi
Kāpēc ir svarīga korelācijas analīze?Korelācijas analīze palīdz atpazīt saistību starp diviem mainīgajiem pirms detalizētas regresijas analīzes veikšanas.
Kā interpretēt R² regresijas analīzē? R² 0,26 nozīmē, ka 26 % no atkarīgā mainīgā (pārdošanas apjoma) variācijas izskaidro neatkarīgie mainīgie.
Kāda ir atšķirība starp korelāciju un regresiju? Ar korelāciju mēra saistību starp diviem mainīgajiem, bet ar regresiju novērtē vairāku neatkarīgo mainīgo ietekmi uz atkarīgo mainīgo.
Kā pārbaudīt statistisko nozīmīgumu? Statistisko nozīmīgumu pārbauda, izmantojot p-vērtību; p-vērtības, kas mazākas par 0,05, tiek uzskatītas par nozīmīgām.
Kāda nozīme ir beta koeficientiem? Beta koeficienti parāda neatkarīgo mainīgo relatīvo ietekmi uz atkarīgo mainīgo.


