Normālais sadalījums ir galvenais jēdziens varbūtību teorijā un statistikā. Jebkurā vienmērīgi sadalītu datu kopā mēs novērojam tā saukto zvanu līkni, kas bieži sastopama aptaujās un pārdošanas analīzēs. Šajā pamācībā uzzināsiet, kā ar Excel palīdzību aprēķināt un vizualizēt aptaujas normālo sadalījumu, lai noteiktu galvenās varbūtības. Izmantojot šīs prasmes, jūs varēsiet ne tikai labāk izprast savus datus, bet arī izmantot tos, lai pieņemtu pamatotus lēmumus.
Galvenās atziņas
- Jūs iemācīsieties soli pa solim aprēķināt normālo sadalījumu programmā Excel.
- Uzzināsiet, kā vizualizēt normālo sadalījumu grafiski.
- Jūs sapratīsiet, kā aprēķināt konkrētu notikumu varbūtības.
Soli pa solim
Pirmkārt, jums jāpārliecinās, ka visi nepieciešamie dati ir pieejami Excel izklājlapā. Šie dati ir, piemēram, aptaujas dati par pārdošanas apjomiem.
Normālā sadalījuma vizualizācija
Lai vizualizētu pārdošanas apjomu normālo sadalījumu grafiski, rīkojieties šādi:
Vispirms Excel izklājlapā atlasiet pārdošanas datus un kopējiet tos jaunā slejā. Izvēlnes joslā noklikšķiniet uz "Insert" un izvēlieties "Chart". Šeit izvēlieties histogrammu, lai vizualizētu sadalījumu. Varat izvēlēties tukšu histogrammu, lai attēlotu jūsu datu noklusējuma vērtības.

Ar peles labo pogu noklikšķiniet uz diagrammas un izvēlieties "Atlasīt datus". Atvērtajā logā pievienojiet savus pārdošanas datus kā pirmo datu sēriju. Sērijas vērtībās atlasiet visus datu ierakstus, turot nospiestu taustiņu Shift un izvēloties vērtības.
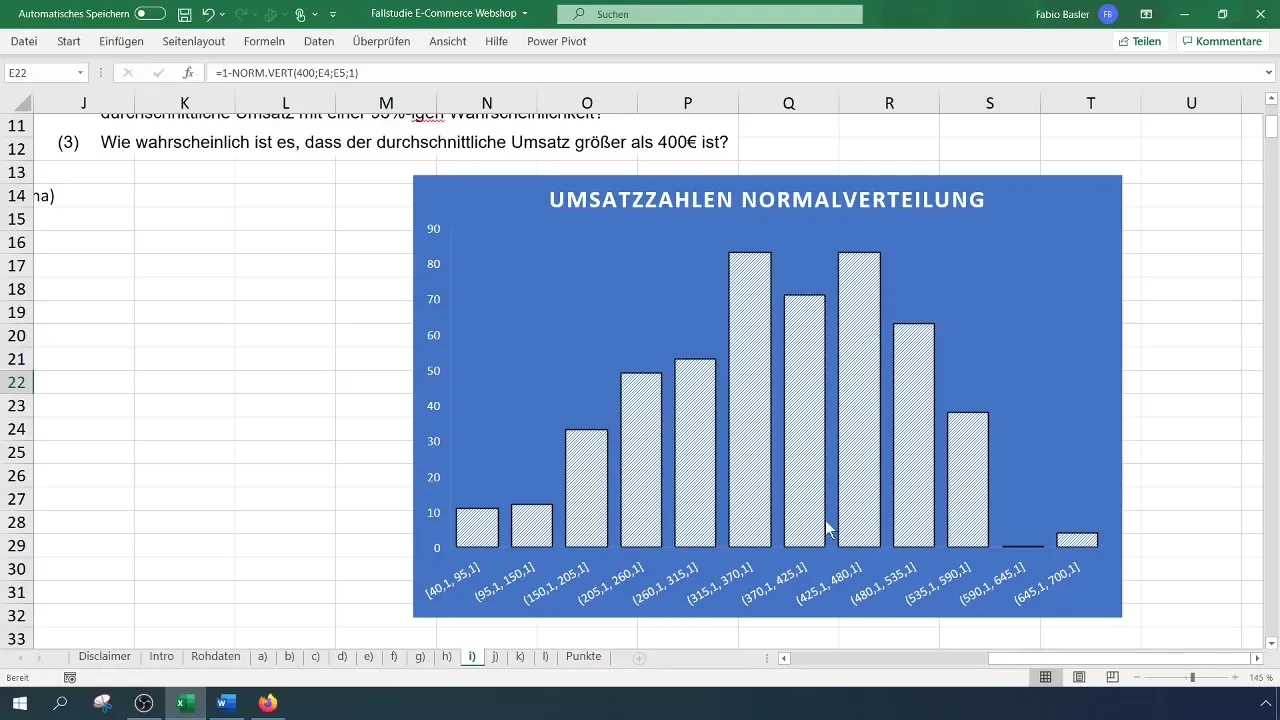
Kad dati ir attēloti histogrammā, varat pielāgot diagrammas nosaukumu, lai padarītu to reprezentatīvāku. Piemēram, mainiet virsrakstu uz "Pārdošanas rādītāji normālais sadalījums". Pārliecinieties, vai ir atpazīstama zvana līkne; tas norāda uz normālu sadalījumu.
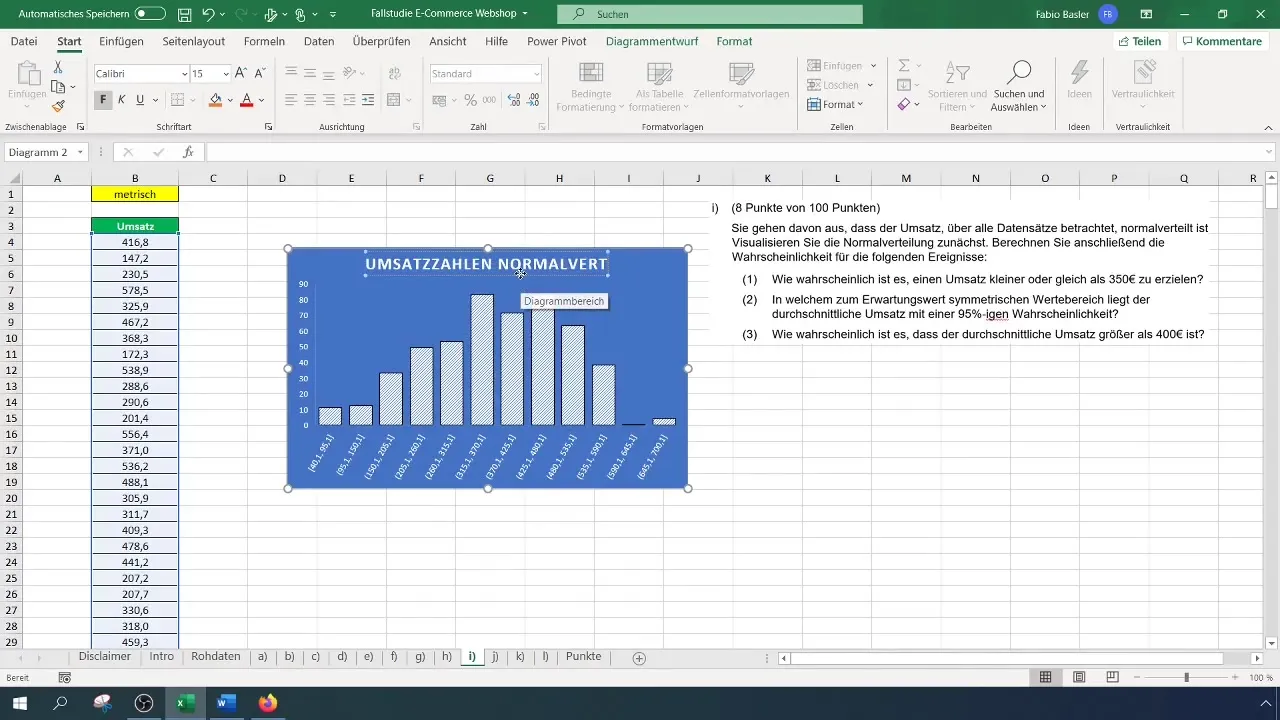
Varbūtību aprēķināšana
Nākamais uzdevums ir noteikt varbūtību, ka apgrozījums ir mazāks vai vienāds ar 350 eiro. Lai to izdarītu, jums ir nepieciešama pārdošanas datu vidējā vērtība un standartnovirze.
Lai aprēķinātu vidējo vērtību, izmantojiet formulu =vidējais(A1:A100) (šeit A1:A100 aizstāj faktisko datu diapazonu). Jūsu piemērā tas varētu radīt vidējo apgrozījumu 369 eiro apmērā.
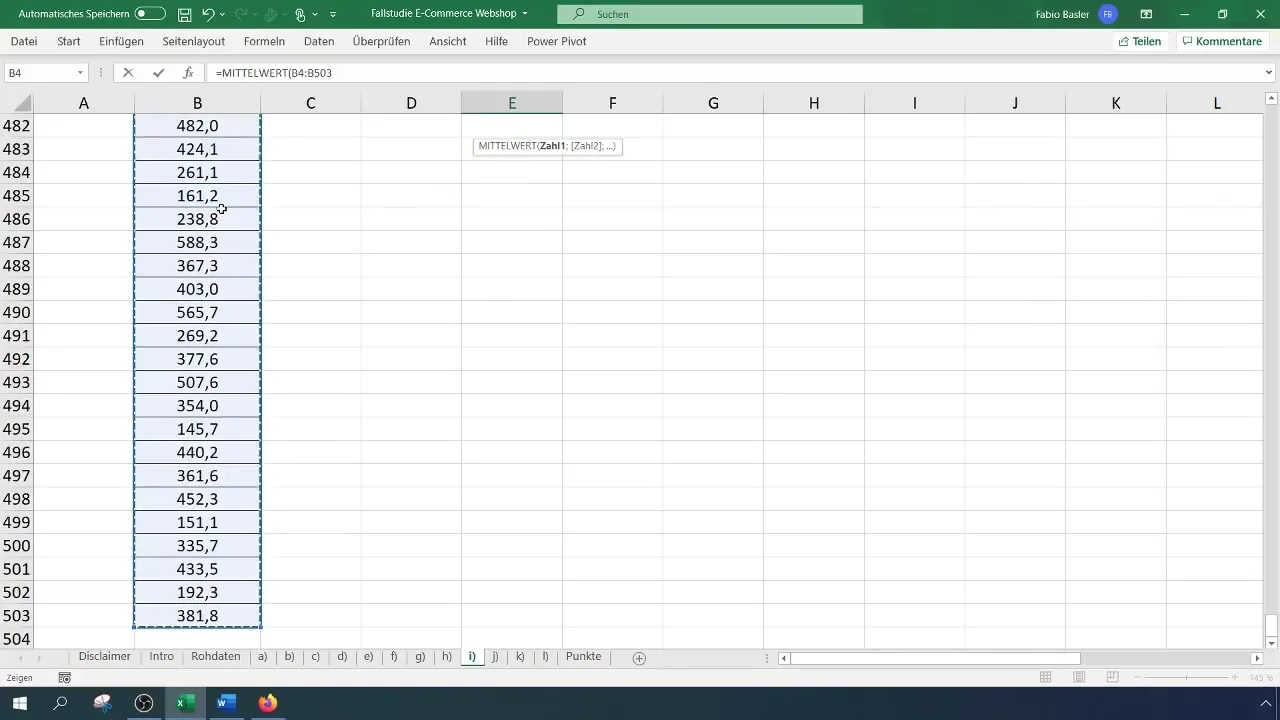
Standarta novirzei izmantojiet formulu =STDEVP(A1:A100), un jūsu gadījumā tas varētu dot aptuveni 124,12 euro.
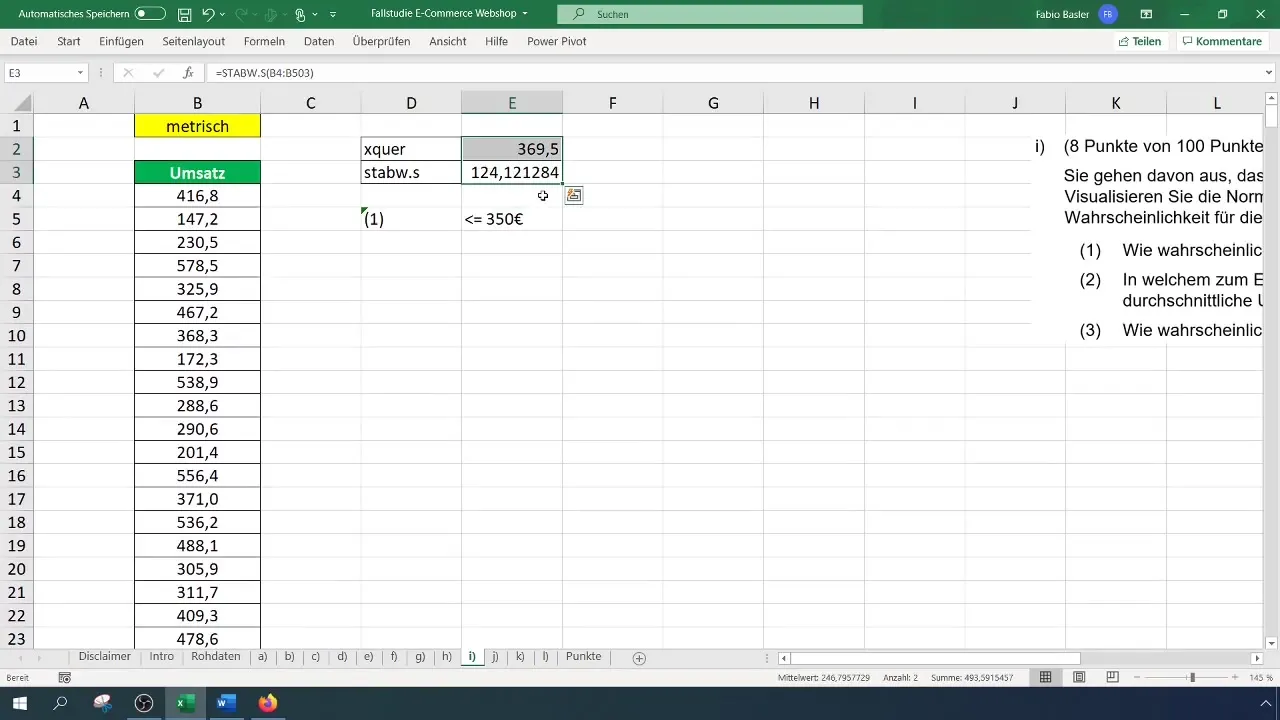
Tagad jūs varat aprēķināt varbūtību, ka apgrozījums būs 350 eiro. To var izdarīt, izmantojot formulu: =NORM.VERT(350; vidējais; standartnovirze; TRUE). Ievadiet attiecīgās vērtības un nospiediet Enter.
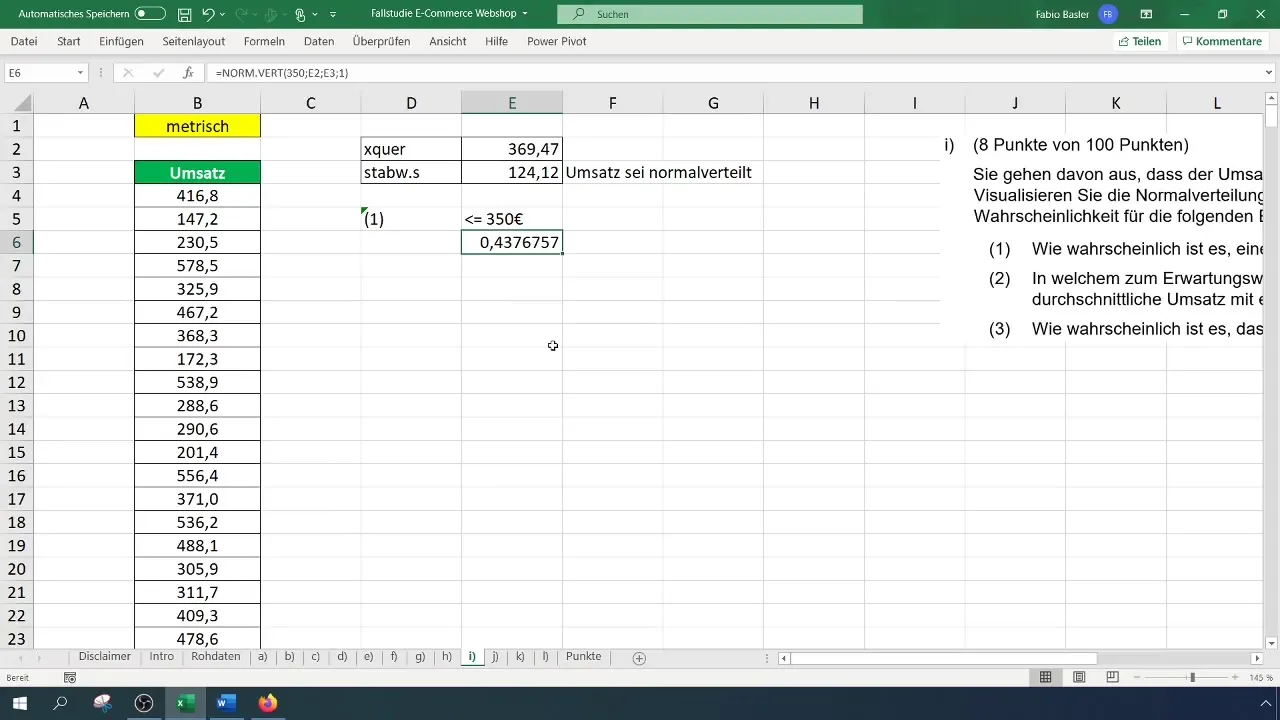
Šī aprēķina rezultāts varētu parādīt, ka varbūtība, ka apgrozījums būs mazāks vai vienāds ar 350 eiro, ir aptuveni 43,8 %. Lai to vizualizētu, varat formatēt vērtības un pārslēgties uz procentuālo attēlojumu.
Simetrisko vērtību diapazona aprēķināšana ap sagaidāmo vērtību
Nākamais uzdevums ir noteikt simetrisko vērtību diapazonu ap sagaidāmo vērtību ar 95% varbūtību. Lai to izdarītu, jānosaka kvantitatīvā vērtība 95 %.
To var izdarīt, ievadot šūnā formulu =NORM.S.INV(0,95), kas dod kvantiļa vērtību 1,65.
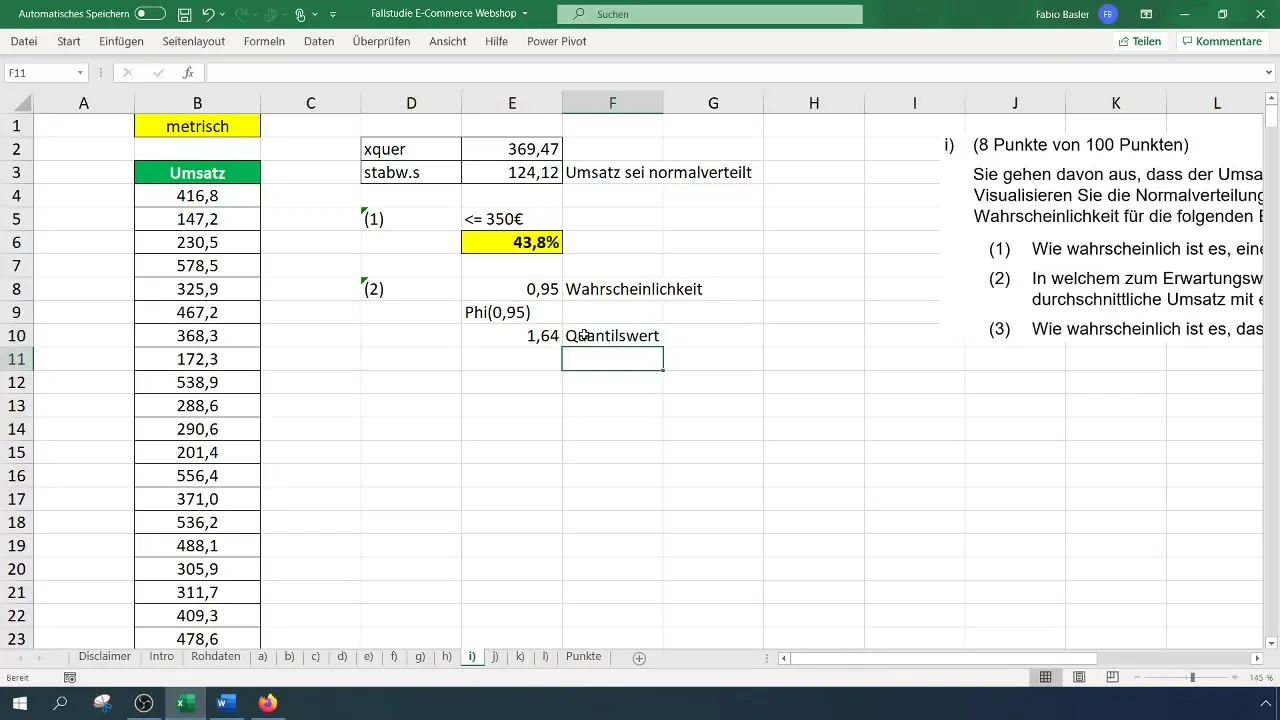
Tagad ievietojiet šo aprēķinu vienādojumā, lai atrastu vērtību diapazonu. Formula varētu izskatīties šādi: Paredzamā vērtība + (standartnovirze * kvantiļa vērtība). Ievietojiet atbilstošās vērtības un aprēķiniet simetrisko vērtību diapazonu.
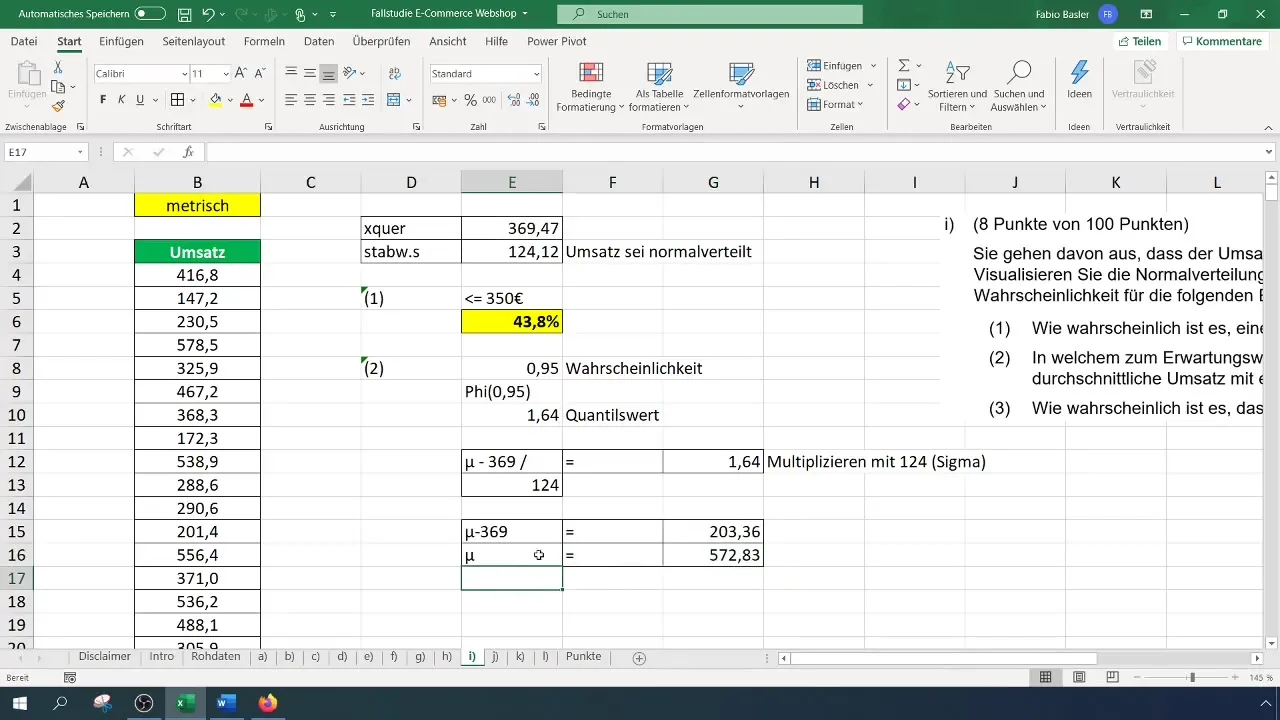
Piemēram, ja saņemta vērtība 572 eiro, tas nozīmē, ka var sagaidīt pārdošanu šajā diapazonā ar 95% varbūtību.
Lielāku pārdošanas apjomu varbūtība
Pēdējā aprēķinā jūs noteiksiet varbūtību, ka apgrozījums ir lielāks par 400 eiro. Lai to izdarītu, izmantojiet formulu =1 - NORM.VERT(400; vidējais; standartnovirze; TRUE).
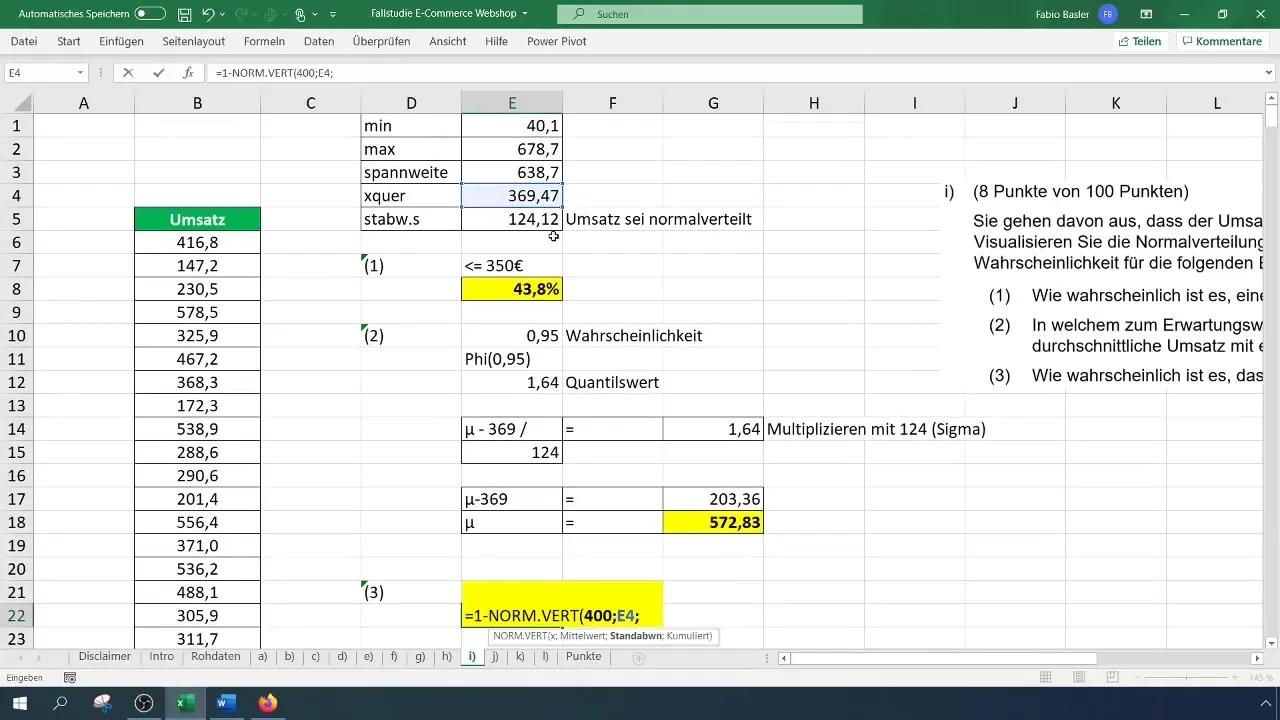
Arī šeit varbūtība varētu būt aptuveni 40 %. Ir lietderīgi rūpīgi pārbaudīt šīs vērtības. Ja aplūkojat skalu histogrammā, varat redzēt lielāku pārdošanas apjomu procentuālās daļas konsekvenci.
Kopsavilkums
Šajā rokasgrāmatā esat iemācījušies, kā Excel programmā izmantot normālo sadalījumu, lai aprēķinātu varbūtības. Balstoties uz praktiskiem piemēriem no aptaujas, esat iemācījušies strādāt ar datiem gan grafiski, gan matemātiski. Šo jēdzienu izpratne palīdzēs jums veiksmīgi īstenot statistisko analīzi savos projektos.


