Als je bezig bent met de analyse van gegevens, zul je al snel merken dat het belangrijk is om verbanden te kunnen leggen tussen verschillende variabelen. In deze tutorial zal ik je laten zien hoe je in Excel een contingentieanalyse uitvoert om de relatie tussen twee nominale variabelen te kwantificeren. We zullen hiervoor een praktisch voorbeeld uit de auto-industrie gebruiken om te begrijpen hoe je waardevolle inzichten uit de gegevens kunt halen.
Belangrijkste inzichten
- Contingentieanalyse maakt het mogelijk om verbanden tussen twee nominale variabelen te onderzoeken.
- De contingentiecoëfficiënt kwantificeert de sterkte van de relatie.
- Een draaitabel in Excel is een onmisbaar gereedschap voor de analyse.
Stapsgewijze handleiding voor contingentieanalyse
Stap 1: Gegevens voorbereiden
Voordat je begint met de contingentieanalyse in Excel, dien je ervoor te zorgen dat de gegevens waarmee je werkt correct zijn voorbereid. Verwijder alle filterinstellingen om een volledig zicht op de gegevens te garanderen.
Maak een overzicht met de productieleider en de informatie over afkeur als nominale gegevens. In ons geval richten we ons op de ploegleiders A, B en C en laten we alle andere vertegenwoordigers buiten beschouwing.
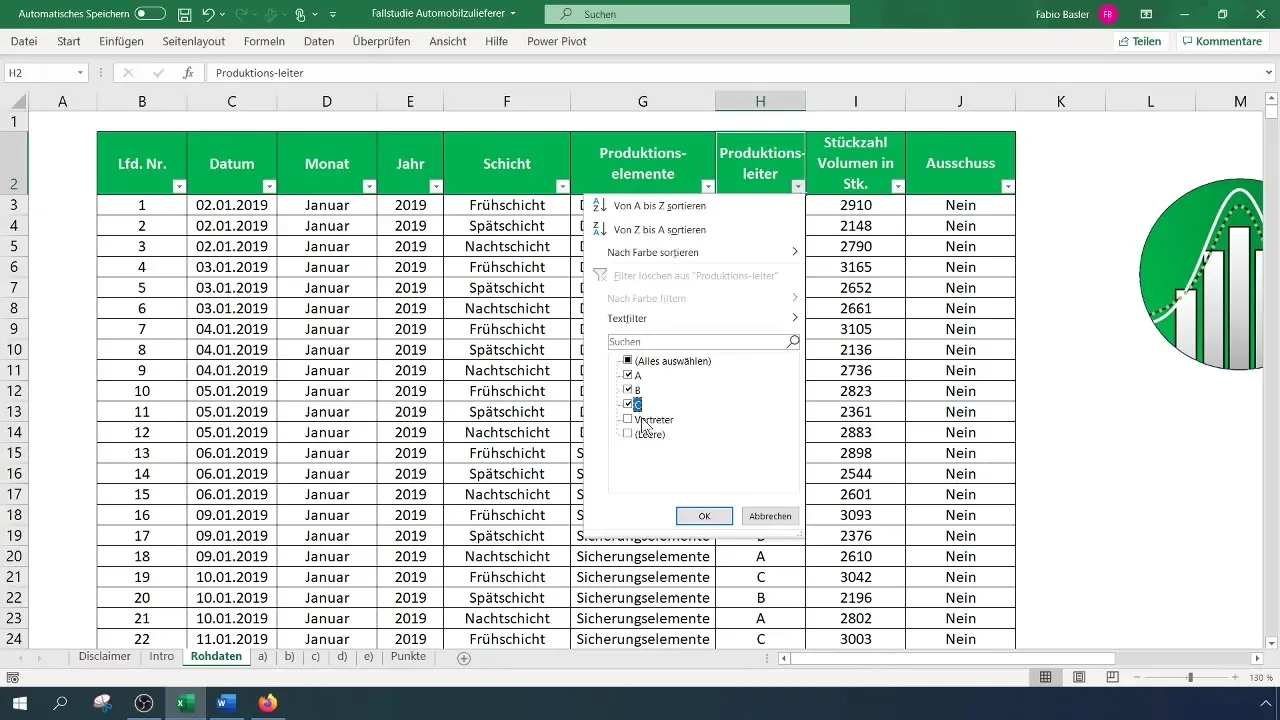
Stap 2: Draaitabel maken
Om de contingentieanalyse uit te voeren, dien je een tweedimensionale frequentieverdeling te creëren die laat zien hoe vaak elke combinatie van productieleider en afkeur voorkomt. Ga hiervoor naar de menubalk 'Invoegen' en kies 'Draaitabel'.
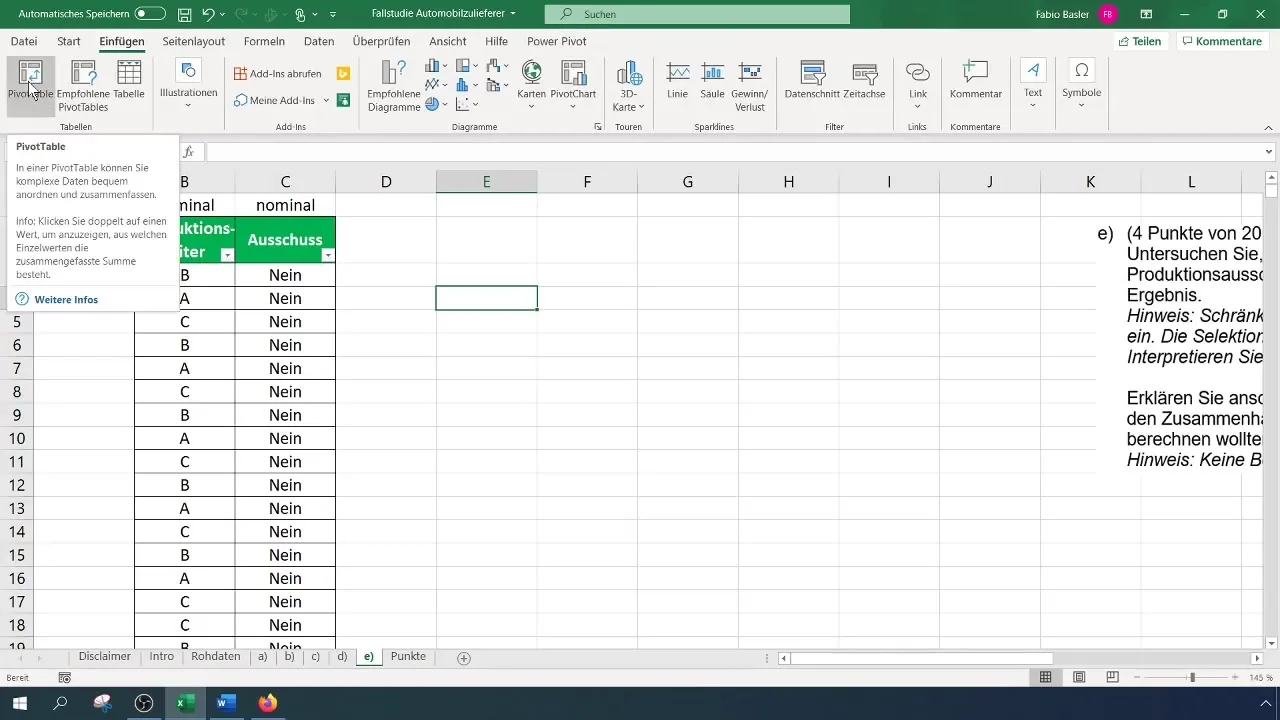
Selecteer het relevante gegevensbereik en bevestig dat de koppen correct zijn herkend. Je draaitabel is nu gemaakt en je kunt de velden voor productieleider en afkeur tegenover elkaar zetten.
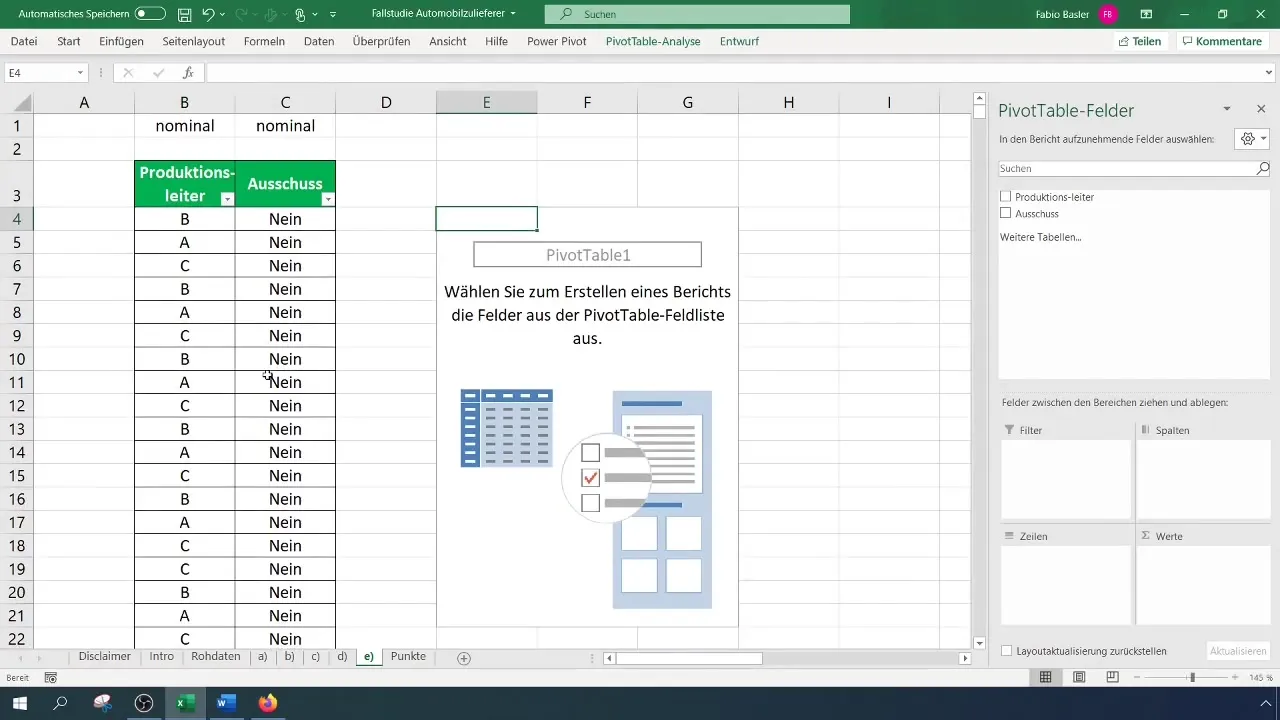
Stap 3: Frequenties analyseren
Nadat je je draaitabel hebt gemaakt, kun je de absolute frequenties bepalen. Plaats de kenmerken in de rijen en kolommen van de draaitabel. Dit laat zien hoeveel afkeuringen er per ploegleider zijn geweest.
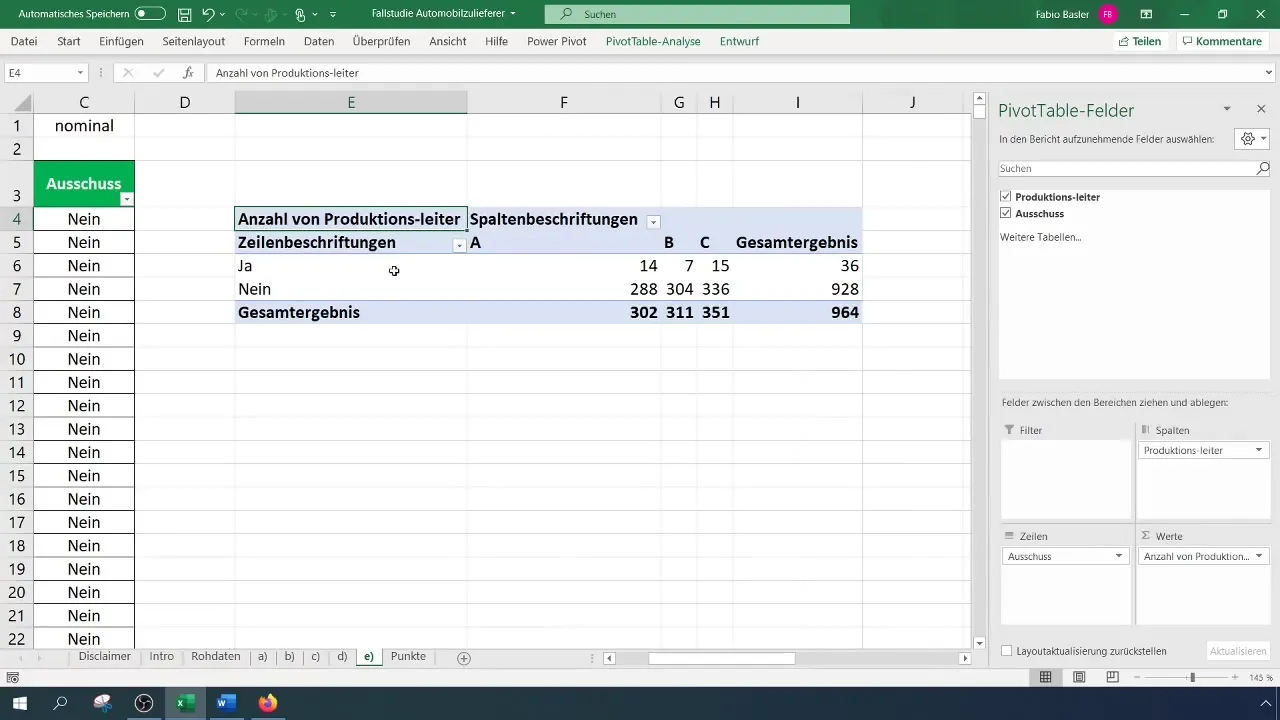
Bekijk de draaitabel en analyseer de resultaten. Let vooral op de verdeling van de variabelen om te bepalen bij welke ploegleider de afkeur het meest of het minst voorkomt.
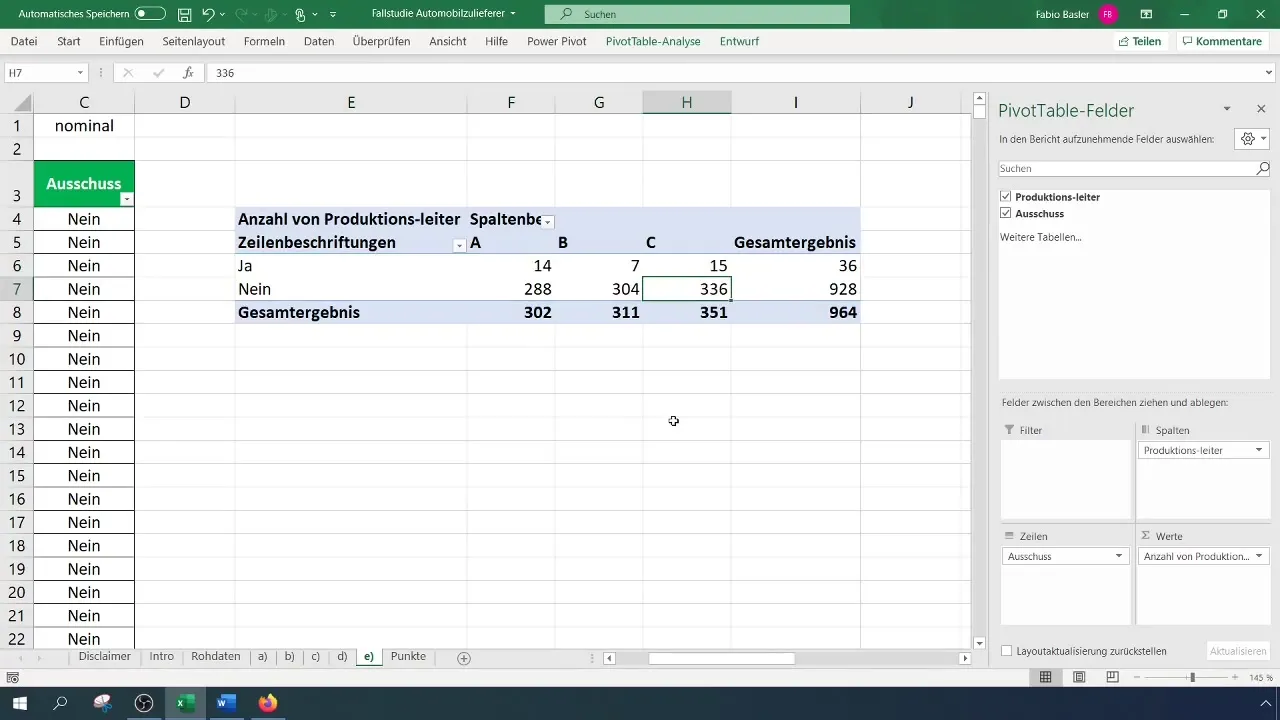
Stap 4: Verwachte frequenties berekenen
Om de contingentiecoëfficiënt te berekenen, dien je de verwachte absolute frequenties te bepalen. De algemene formule is: (N_{ij} = \frac{(R_i \times C_j)}{N}), waarbij (R) de rijmargefrequentie is en (C) de kolommargefrequentie.
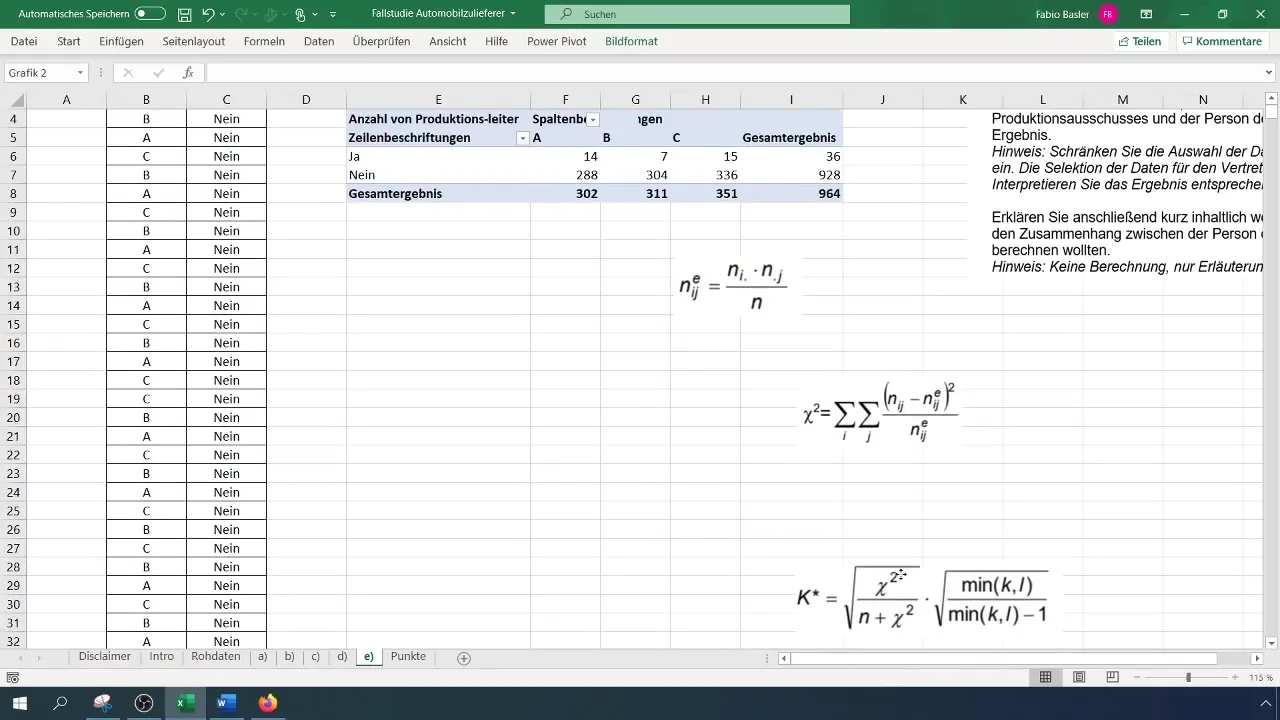
Pas deze berekening toe op de waarden in je draaitabel. Zorg ervoor dat je een aparte tabel voor de verwachte frequenties maakt om de analyses overzichtelijk te houden.
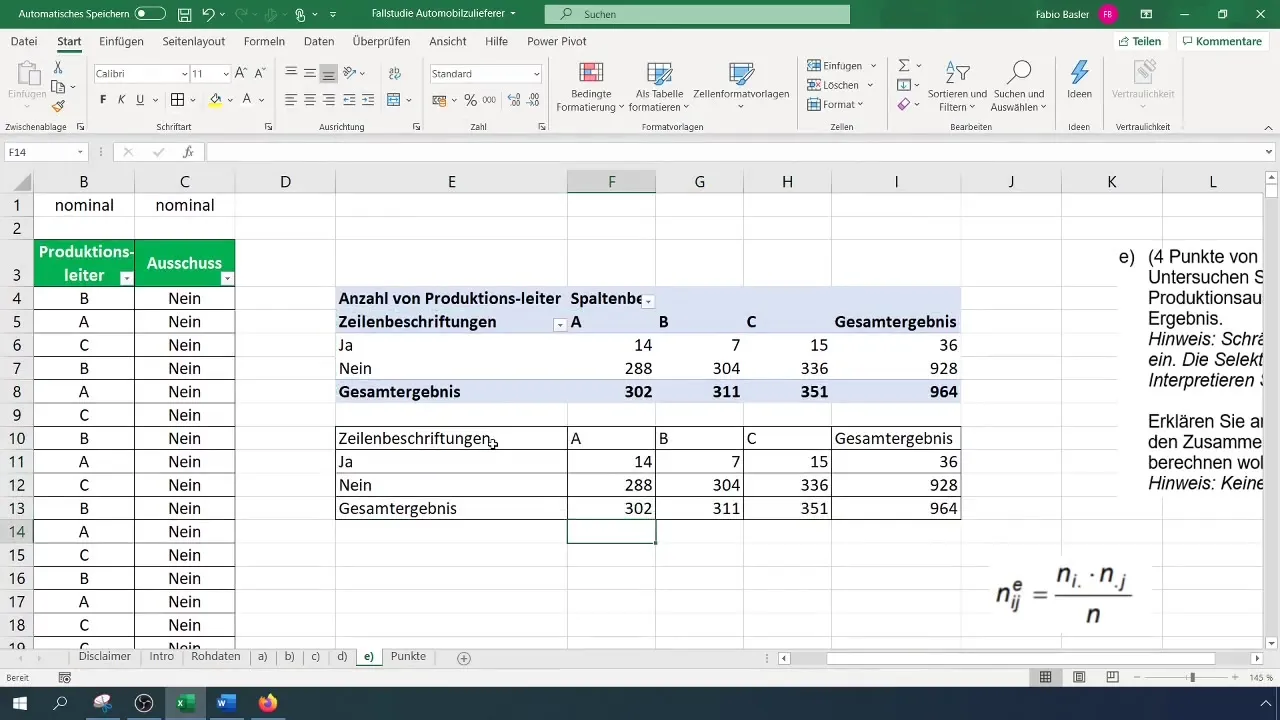
Stap 5: Chi-kwadraatwaarde berekenen
Bereken nu de chi-kwadraatwaarde om de relatie tussen de variabelen kwantitatief vast te leggen. De formule is:
[ \chi^2 = \sum \frac{(O{ij} - E{ij})^2}{E_{ij}} ]
Hierbij is (O) de waargenomen frequentie en (E) de verwachte frequentie.
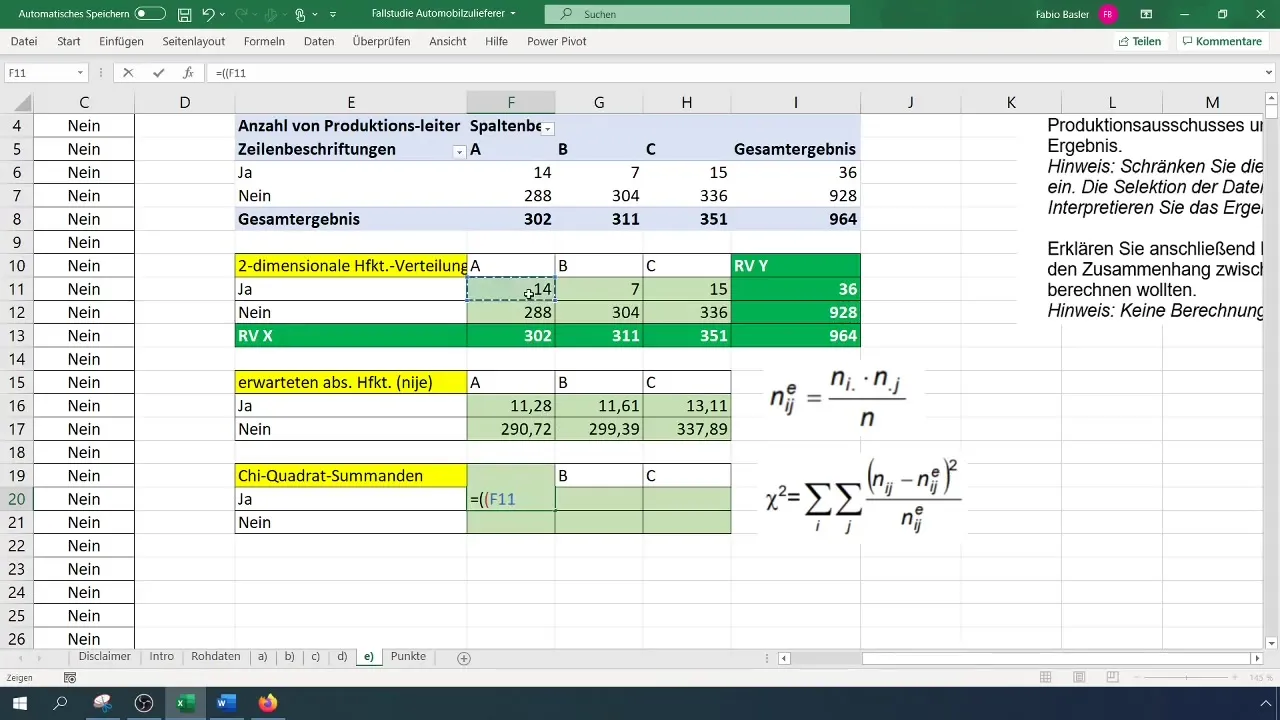
Bereken de verschillen tussen de waargenomen en verwachte frequenties en kwadrateer deze.
Stap 6: Contingentiecoëfficiënten berekenen
De laatste stap is om de contingentiecoëfficiënt te berekenen. De formule voor berekening is:
[ K = \sqrt{\frac{\chi^2}{N}} ]
Gebruik de eerder berekende Chi-kwadraatwaarde en het totale aantal observaties (N).
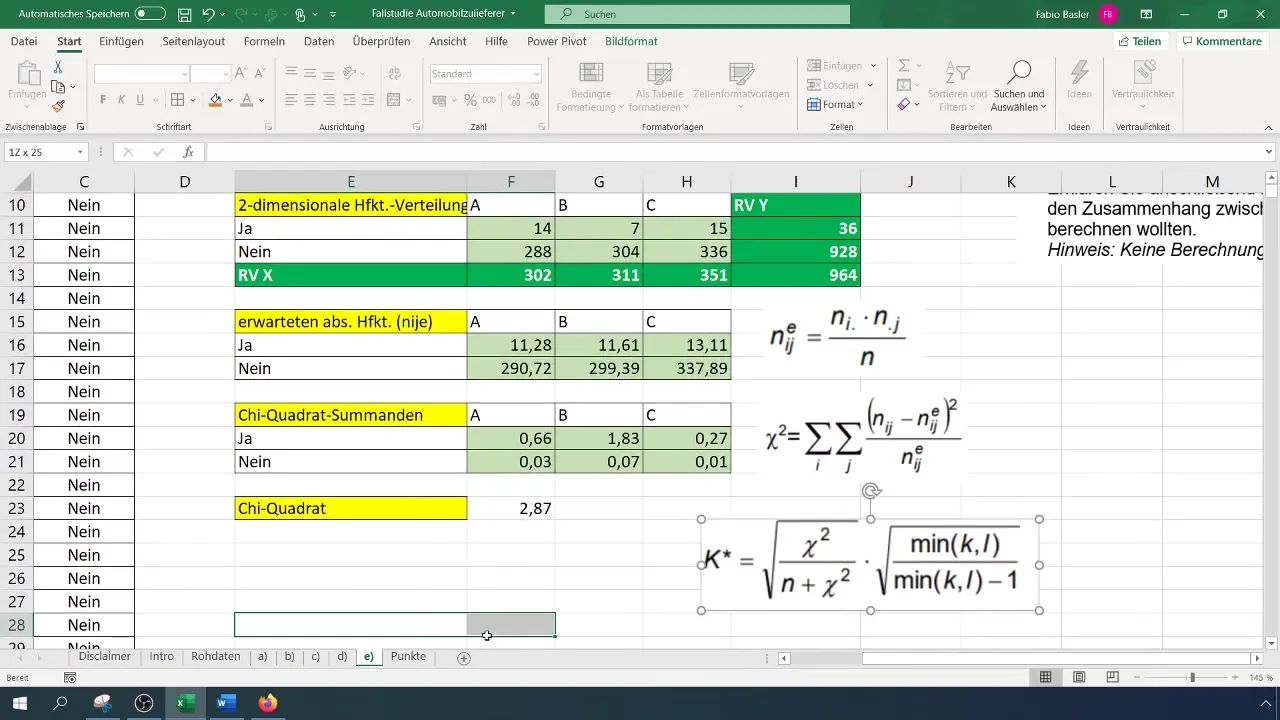
Nadat je de contingentiecoëfficiënt hebt berekend, kun je het resultaat interpreteren. Onze analyse heeft aangetoond dat de contingentiecoëfficiënt van 0,077 een zwak verband tussen de variabelen laat zien.
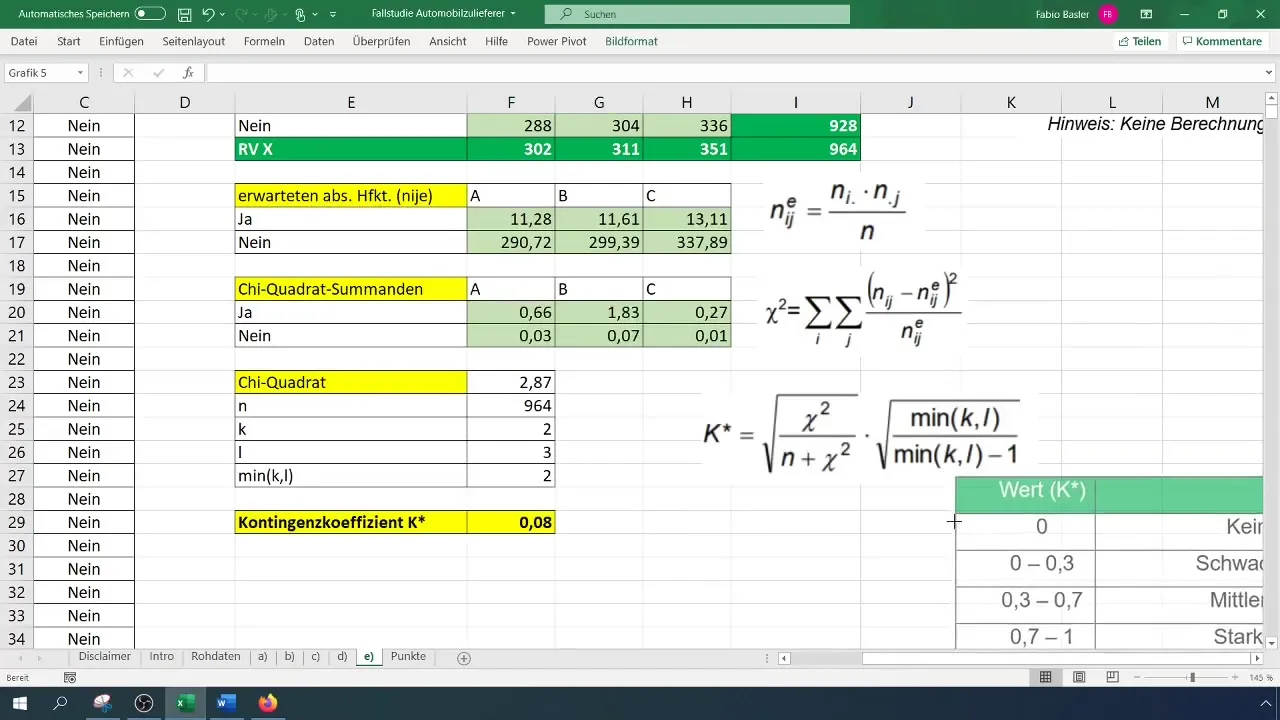
Stap 7: Interpretatie van de resultaten
De laatste stappen van je analyse bestaan uit het interpreteren van de resultaten. Een contingentiecoëfficiënt dicht bij 0 geeft aan dat er nauwelijks verband bestaat tussen de variabelen. Een waarde van 0,08 duidt erop dat de productiemanager geen significante invloed heeft op het voorkomen van afval.
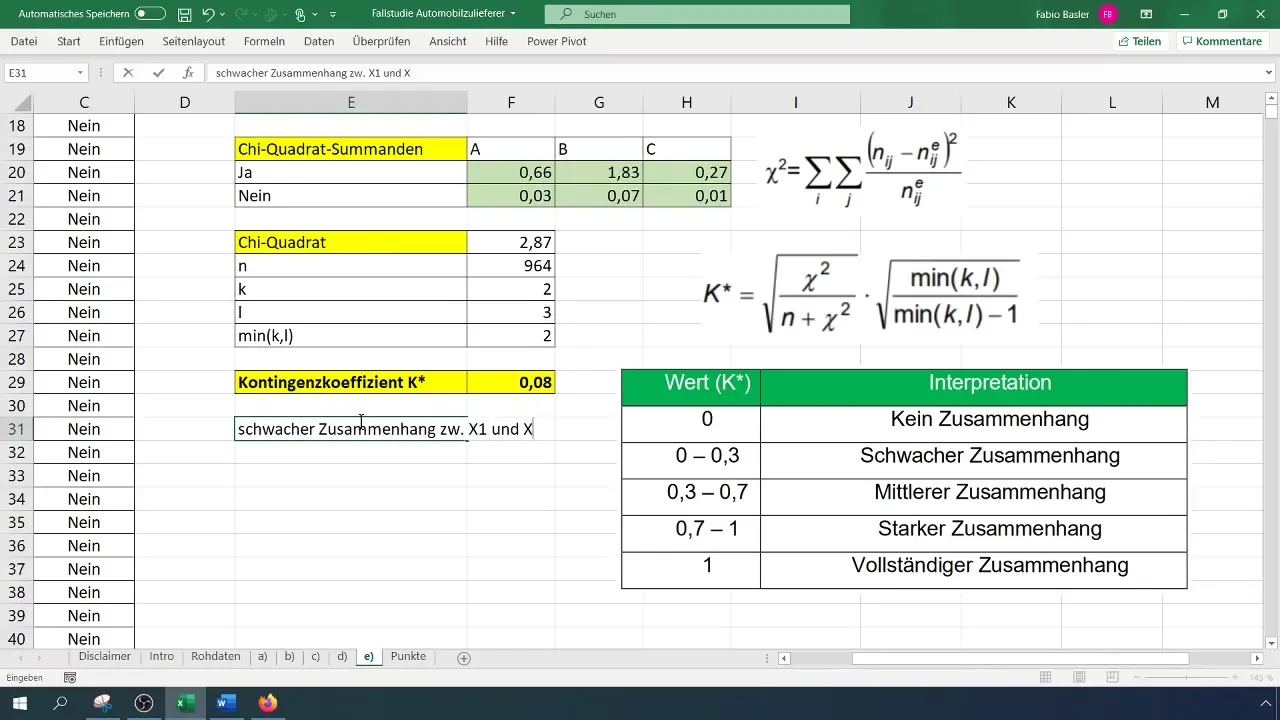
Samenvatting
In deze handleiding heb je geleerd hoe je de contingentieanalyse in Excel uitvoert om verbanden tussen nominale variabelen te identificeren. Je hebt geleerd hoe je je gegevens voorbereidt, een draaitabel maakt en de nodige berekeningen uitvoert voor de contingentiecoëfficiënt.


