Statistische Tests zijn een essentieel onderdeel van gegevensanalyse en besluitvorming. Vooral in het gebied van de biotechnologie kan het cruciaal zijn om hypothesen over het succespercentage van werkzame stoffen te testen. In dit tutorial leer je hoe je een Eén-steekproeftoets (1-SP-toets) voor de verwachtingswaarde met bekende variantie efficiënt uitvoert in Excel.
Belangrijkste inzichten
Deze handleiding leert je het volgende:
- De theoretische basis van de 1-SP-toets.
- Stappen voor het uitvoeren van de toets in Excel.
- De interpretatie van de resultaten.
Voorbereiding van de gegevens
Om de 1-SP-toets in Excel uit te voeren, heb je eerst de relevante gegevens nodig. In ons voorbeeld gaan we ervan uit dat je het succespercentage van werkzame stoffen analyseert. Het is bekend dat het gemiddelde succespercentage eerder 59% was, met een standaardafwijking van 19. Je moet eerst je gegevens in een Excel-tabel invoeren.
Zorg ervoor dat je gegevens in kolommen zijn georganiseerd, zodat je er later gemakkelijk toegang toe hebt. Een overzichtelijke structuur helpt je de verschillende stappen makkelijker te volgen.
Testoverzicht
De 1-SP-toets is bedoeld om te controleren of het gemiddelde succeswaarde significant verschilt van een vooraf bepaalde waarde. In dit geval controleren we of het succespercentage van 59% in de toekomst aanzienlijk kan worden verhoogd.
Hypothesen formuleren
De hypotheses die je opstelt voor de test zijn cruciaal:
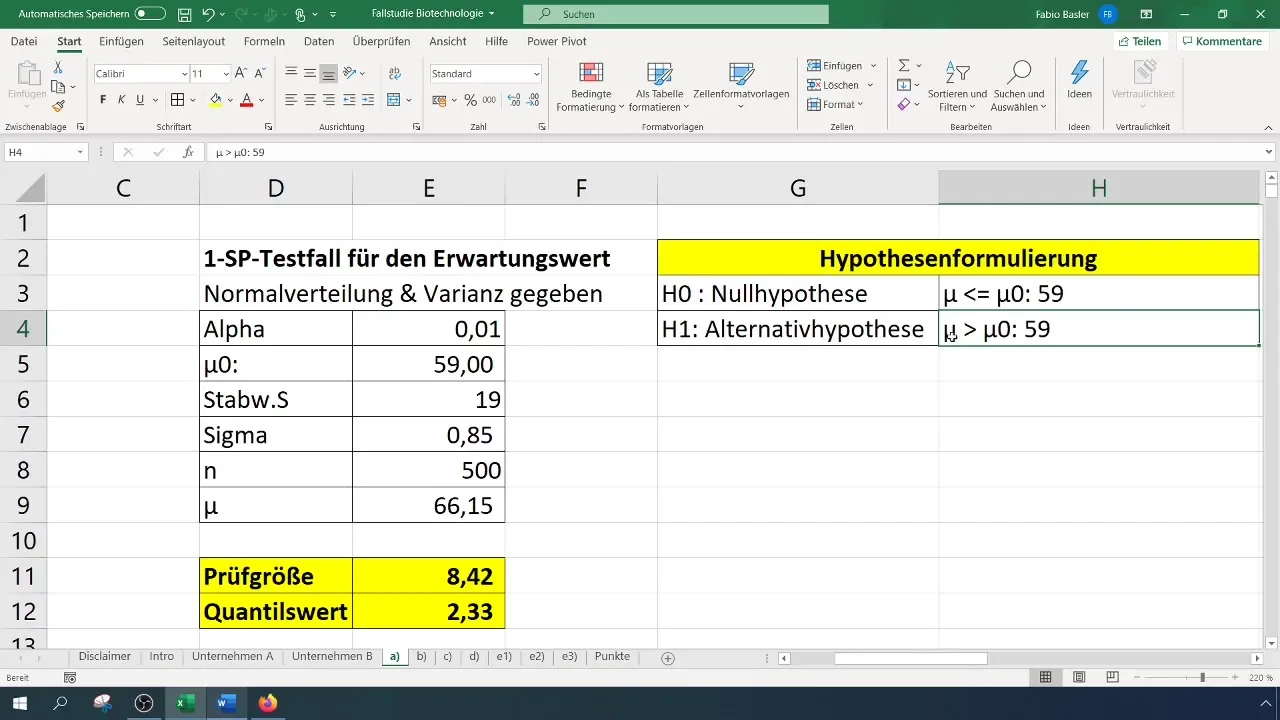
- Nulhypothese (H0): De ware verwachtingswaarde is gelijk aan 59 (σ = 59%).
- Alternatieve hypothese (H1): De ware verwachtingswaarde is groter dan 59%.
Bij het formuleren van de hypotheses moet de focus liggen op wat precies getest moet worden en hoe dat zich in jouw context vertaalt.
Het is belangrijk om het verschil tussen de nulhypothese en de alternatieve hypothese duidelijk te begrijpen, aangezien zij de basis vormen voor de volgende berekeningen.
Verzamelen van de steekproef
Voor onze test nemen we een steekproef van 500 werkzame stoffen. Het is belangrijk op te merken dat de selectie van de steekproef representatief moet zijn en met de juiste methode moet garanderen dat je resultaten realistisch gezien op de totale populatie kunnen worden toegepast.
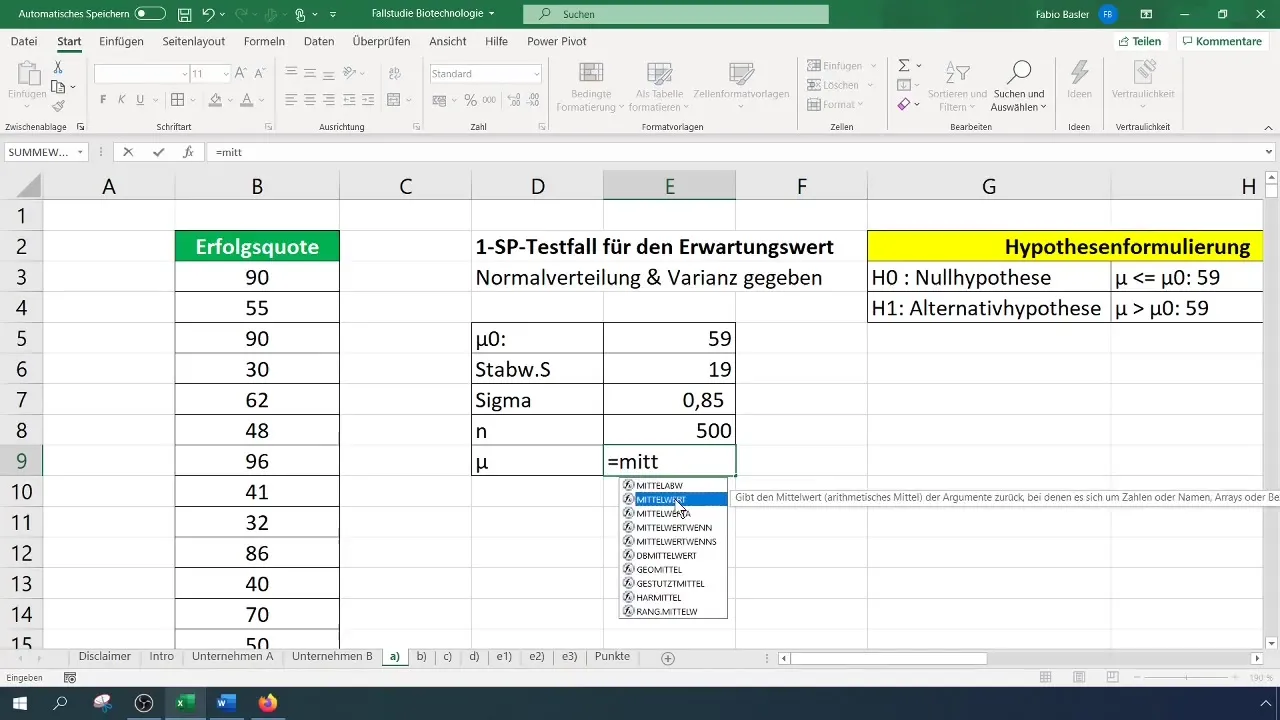
Voor de test bereken je eerst het gemiddelde. Dit moet eenvoudig worden gedaan door de juiste formule in Excel te gebruiken.
Berekening van de toetsingsgrootheid
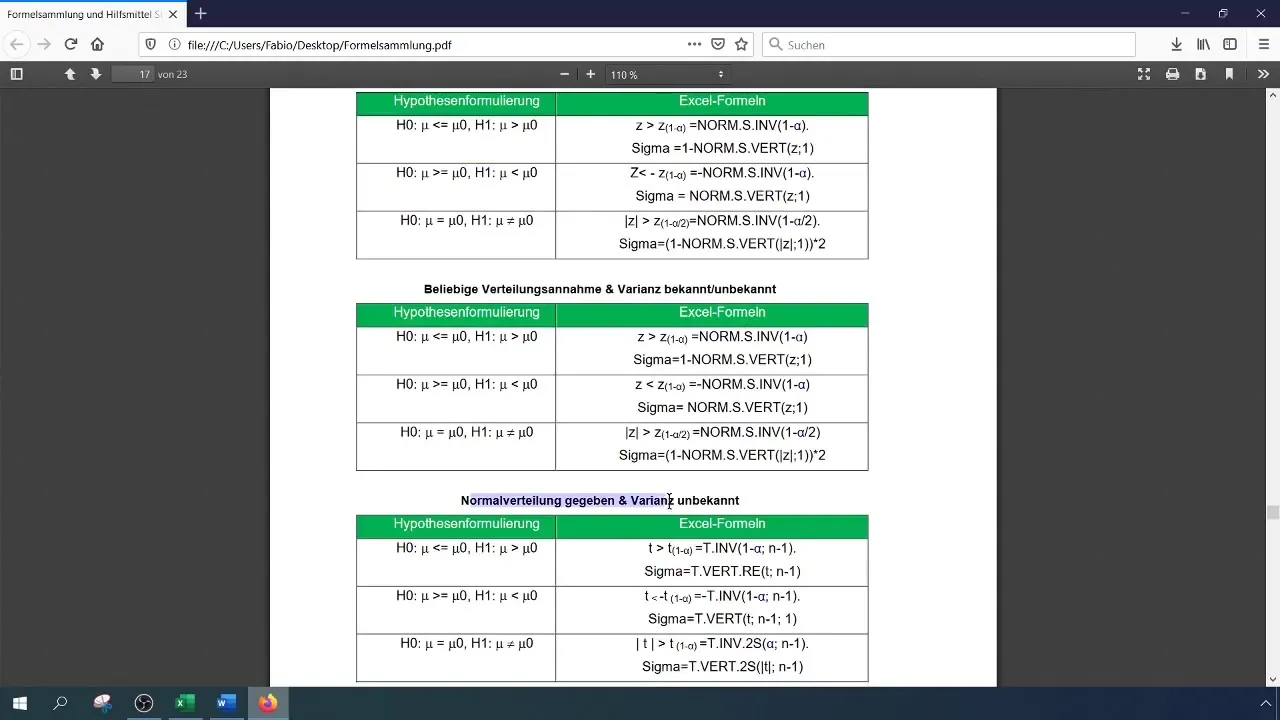
De toetsingsgrootheid voor een 1-SP-test wordt bepaald door de volgende formule:
[ Z = \frac{\bar{x} - \mu_0}{\sigma/\sqrt{n}} ]
Hier staat (\bar{x}) voor het gemiddelde van je steekproef, (\mu_0) voor het aangenomen gemiddelde (in dit geval 59), (\sigma) voor de standaardafwijking (hier 19), en (n) voor het aantal steekproeven (500).
Nadat je de waarden in de formule hebt ingevoerd, bereken de toetsingsgrootheid om te bepalen of deze significant is of niet.
Bepaling van de kritische waarde
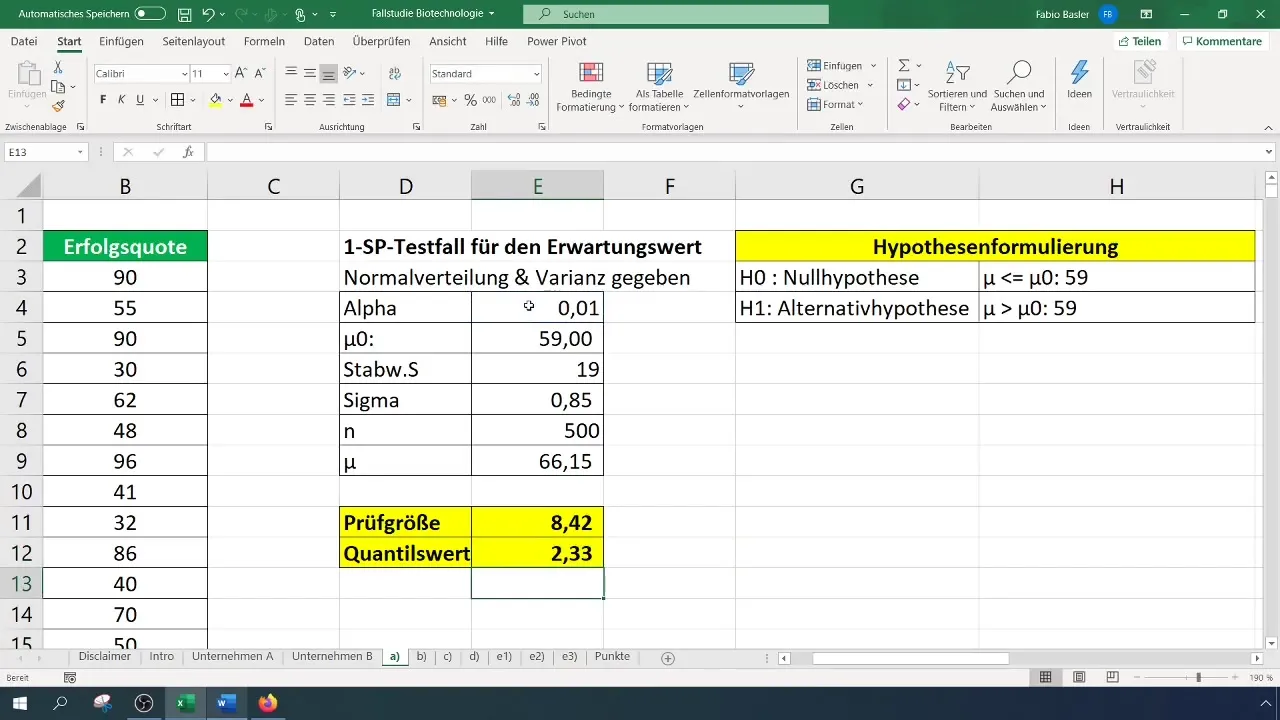
Voor een significantieniveau van 1% (0,01) moet je de kritische waarde aflezen of berekenen. Dit kan met de functie NORM.S.INV in Excel.
De formule is als volgt:
[ \text{NORM.S.INV}(1 - \alpha) ]
Hier is (\alpha) het significantieniveau (0,01). De berekende waarde wordt gebruikt als basis voor de vergelijking met de toetsingsgrootheid.
Uitvoering van de test
Na het verkrijgen van zowel de toetsingsgrootheid als de kritische waarde, vergelijk je beide:
- Als de toetsingsgrootheid groter is dan de kritische waarde, wordt de nulhypothese verworpen.
- Anders kun je de nulhypothese niet verwerpen.
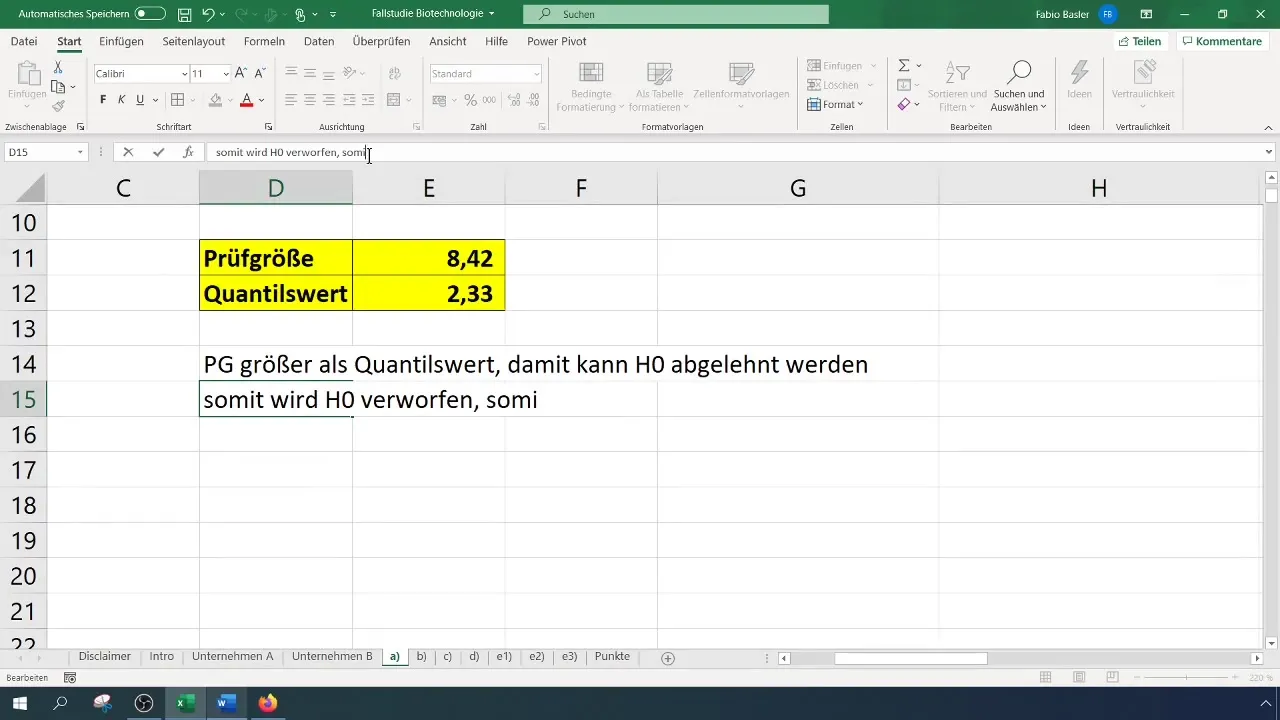
In ons geval resulteert dit in een teststatistiek van 8,4, die de kritieke waarde van 2,33 overschrijdt. Daarom kunnen we de nulhypothese verwerpen. Dit duidt erop dat het succespercentage aanzienlijk is verbeterd.
Interpretatie van de resultaten
Nadat je de test hebt uitgevoerd en de resultaten hebt verkregen, moet je deze in een duidelijke context interpreteren. Het verwerpen van de nulhypothese betekent dat de geteste nieuwe waarde significant verschilt van het verleden, in dit geval 59%.
Deze informatie is van enorm belang voor het strategisch besluitvormingsproces in jouw bedrijf. Het bevestigt dat de inspanningen om het succespercentage te verbeteren effectief zijn geweest.
Samenvatting
In deze zelfstudie heb je geleerd hoe je een 1-SP-test voor de verwachtingswaarde in Excel uitvoert. Aan de hand van een casestudy kon je de stappen van hypthesen formuleren tot gegevensberekening en resultateninterpretatie volgen. Deze kennis is niet alleen waardevol voor wetenschappelijke analyses, maar ook voor praktische toepassingen in een bedrijfscontext.
Veelgestelde vragen
Wat is de 1-SP-test?De 1-SP-test is een statistische test om te controleren of het gemiddelde van een steekproef significant afwijkt van een vooraf bepaalde waarde.
Hoe formuleer ik hypothesen voor de test?De hypothesen bestaan uit een nulhypothese (H0) en een alternatieve hypothese (H1) die de te onderzoeken toestand documenteren.
Hoe bereken ik de teststatistiek?De teststatistiek wordt bepaald door de formule ( Z = \frac{\bar{x} - \mu_0}{\sigma/\sqrt{n}} ).
Wat gebeurt er als de teststatistiek groter is dan de kritieke waarde?Als de teststatistiek groter is dan de kritieke waarde, wordt de nulhypothese verworpen.
Welke rol speelt het significantieniveau?Het significantieniveau geeft aan met welke waarschijnlijkheid je een fout accepteert als je de nulhypothese onterecht verwerpt.


