Statistische vergelijking met Excel: Tweesteekproeven t-toets

De tweesteekproef-t-toets is een essentieel instrument in de statistiek wanneer je het verschil tussen twee gemiddelden wilt onderzoeken. In deze tutorial leer je hoe je deze test eenvoudig en effectief uitvoert in Excel. Aan de hand van een voorbeeld uit de biotechnologie zul je leren hoe je succespercentages van twee concurrerende bedrijven kunt vergelijken en statistisch kunt analyseren.

Belangrijkste inzichten

• Toepassing van de tweesteekproef-t-toets voor de analyse van het verschil tussen twee gemiddelden.
• Formulering en controle van hypothesen.
• Gebruik van Excel voor het berekenen en weergeven van resultaten.

Stapsgewijze handleiding

Laten we eerst beginnen met het verzamelen van de benodigde gegevens en het uitvoeren van de test in Excel.

Stap 1: Gegevens voorbereiden

Begin met het verzamelen van de ruwe gegevens over de succespercentages van de twee bedrijven. Stel dat je gegevens hebt van bedrijf A en B. Je hebt een steekproef van 100 datapunten per bedrijf.

Stap 2: Steekproefomvang en gemiddelden berekenen

Maak een tabel in Excel om de steekproeven en hun gemiddelden te vergelijken. Bereken eerst de steekproefomvang (N) voor beide bedrijven, evenals het gemiddelde (X).

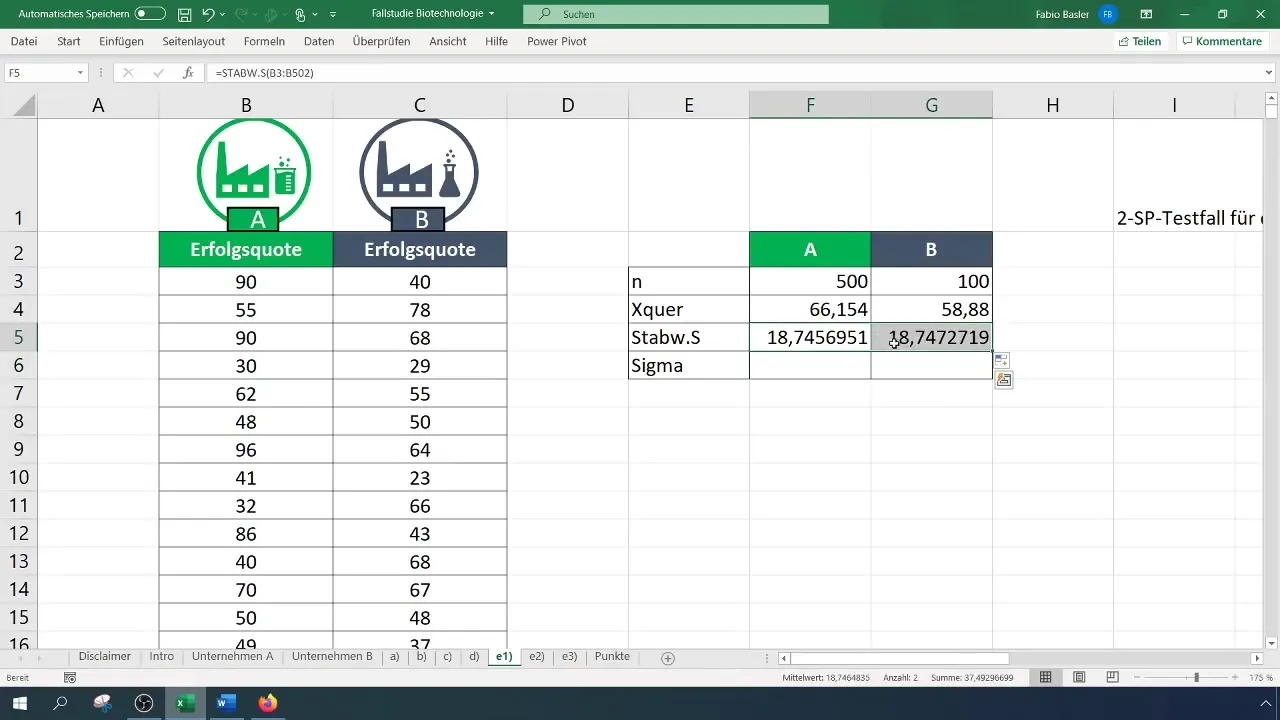
Stap 3: Standaardafwijkingen bepalen

Bereken de standaardafwijking voor beide bedrijven. Deze waarden zijn belangrijk om de variantie en de daaropvolgende berekeningen uit te voeren.

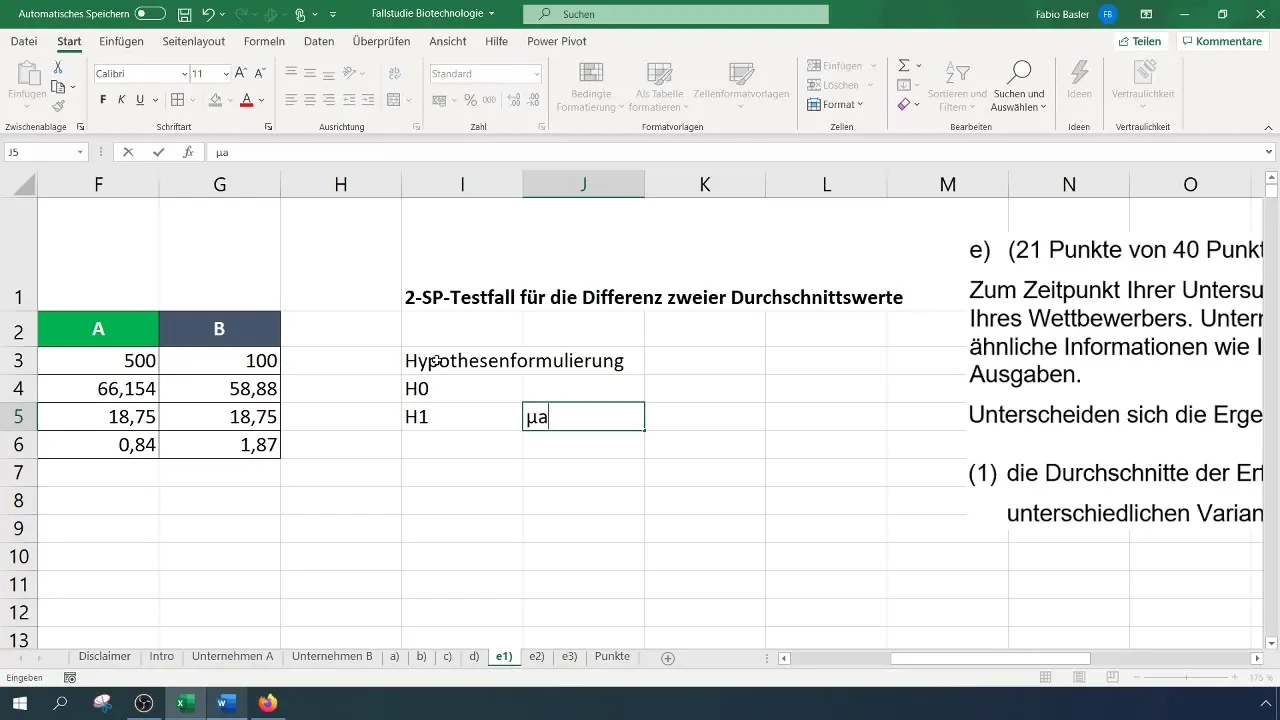
Stap 4: Hypothesen formuleren

Formuleer de nulhypothese (H_0): De gemiddelde succespercentages van bedrijven A en B zijn gelijk. De alternatieve hypothese (H_1): De gemiddelde succespercentages zijn verschillend.

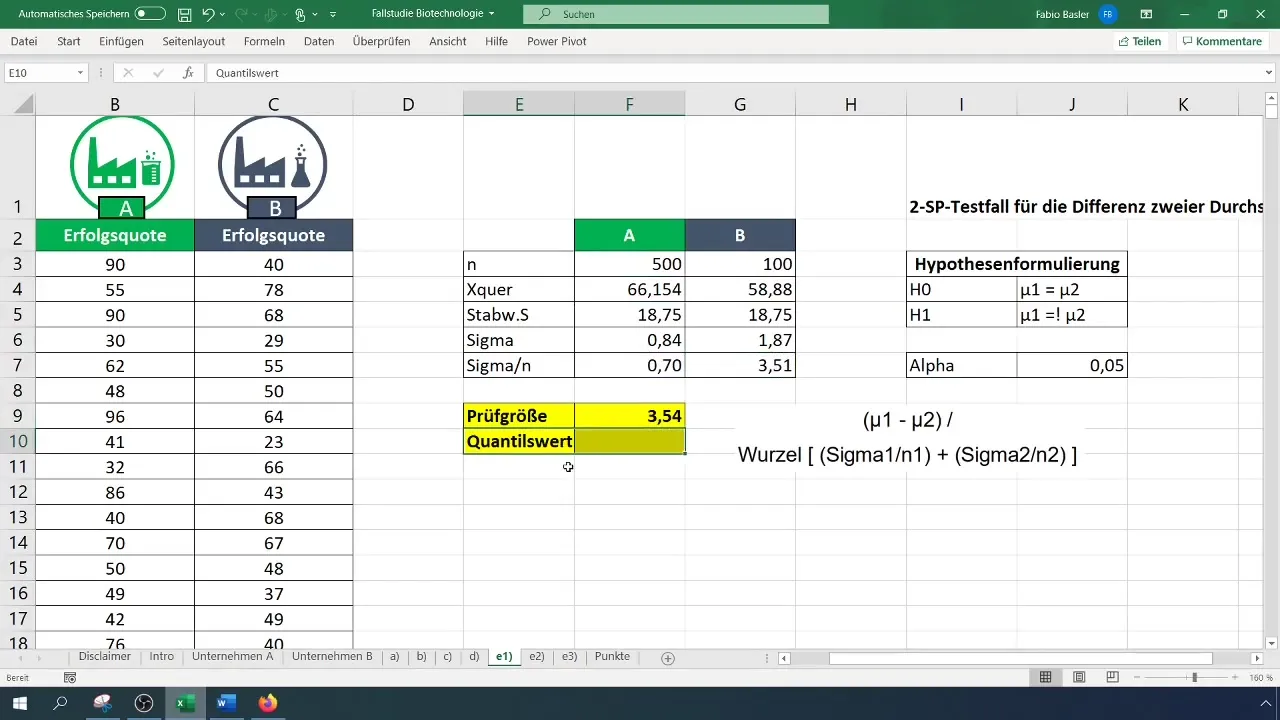
Stap 5: Teststatistiek berekenen

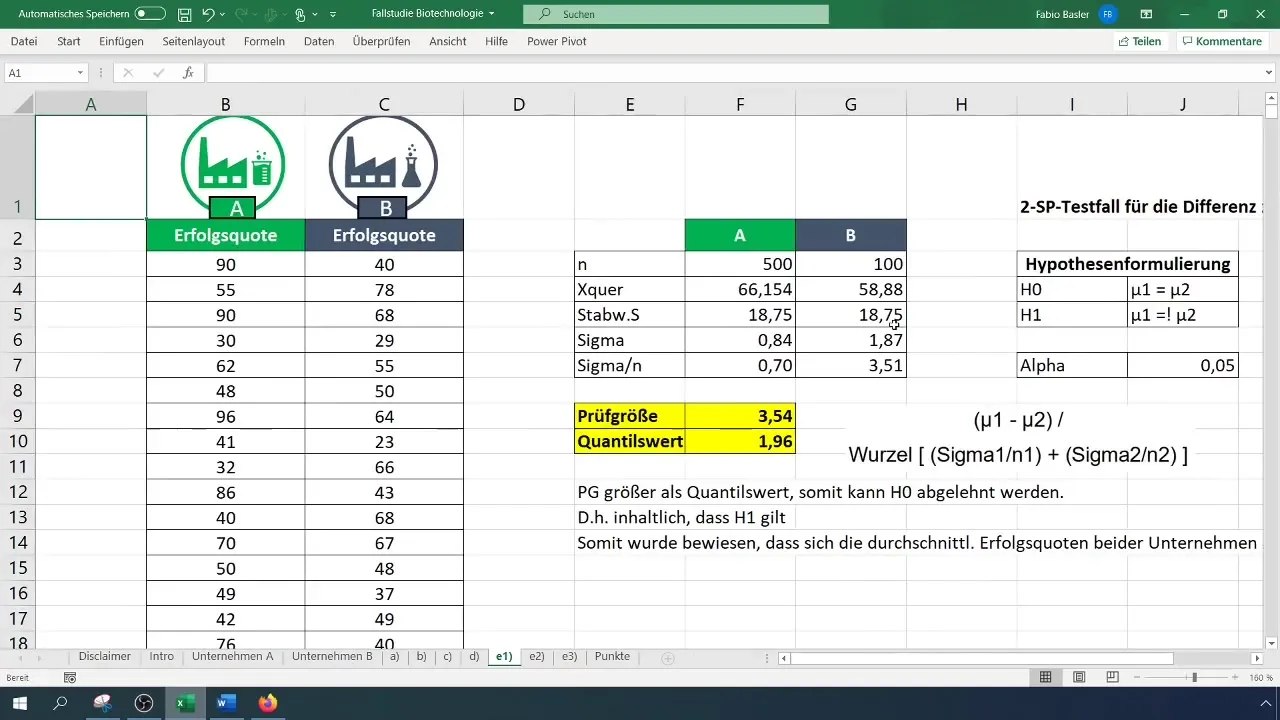
Gebruik de formule voor de t-toets om de teststatistiek te berekenen. Bereken het verschil tussen de gemiddelden en deel dit door de wortel van de som van de varianties per steekproef.

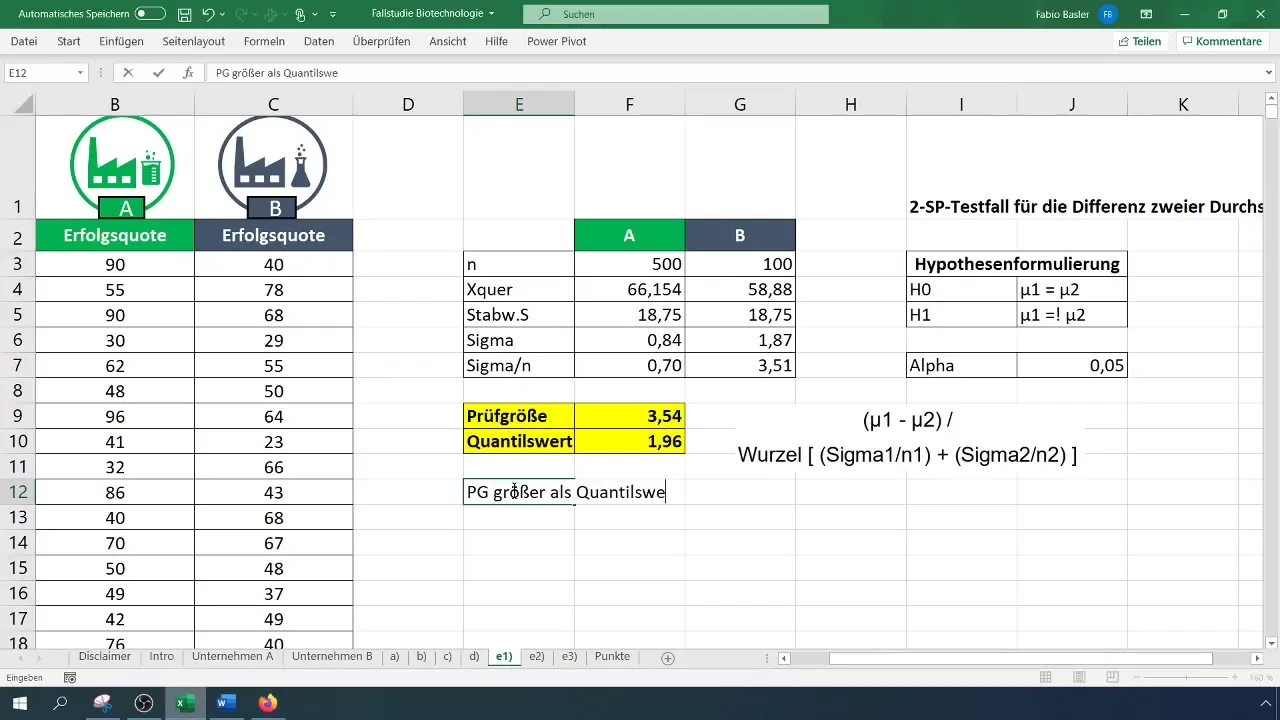
Stap 6: Kritieke waarde bepalen

Gebruik de tweezijdige t-verdeling om de kritieke waarde te vinden. Stel het alfaniveau in op 0,05. Raadpleeg de t-verdelingstabel of bereken de factor rechtstreeks in Excel.

Stap 7: Beslissen over de hypothese

Vergelijk de berekende teststatistiek met de kritieke waarde. Als de teststatistiek groter is dan de kritieke waarde, wijs dan de nulhypothese (H_0) af en bevestig daarmee de alternatieve hypothese (H_1).

Stap 8: Resultaat interpreteren

Interpreteer ten slotte het resultaat. In dit voorbeeld werden de gemiddelde succespercentages van de twee bedrijven als significant verschillend bevonden.

Samenvatting

Je hebt geleerd hoe je een tweesteekproef-t-toets in Excel uitvoert om de verschillen in gemiddelden van twee groepen te onderzoeken. De stappen van data-voorbereiding tot hypothesenformulering en resultateninterpretatie zijn cruciaal om geldige en geïnformeerde beslissingen te nemen.