Chi-kwadraattoets voor aanpassing aan de normale verdeling met Excel

De Chi-kwadraat-aanpassingstest biedt een eenvoudige methode om de hypothese te toetsen of een gegevensreeks een normale verdeling volgt. In deze handleiding leer je hoe je de chi-kwadraattest in Excel kunt uitvoeren om te bepalen of de omzet van smartphones overeenkomt met een normale verdeling. We zullen stap voor stap door het proces gaan, van het maken van een gefrequenteerde tabel tot het berekenen van de testingsgrootte en het vergelijken met de kritische waarde van het chi-kwadraat.

Belangrijkste inzichten

• De Chi-kwadraat-aanpassingstest helpt bij het controleren van normale verdelingen.
• Het is belangrijk om een gefrequenteerde tabel te maken.
• De testingsgrootte wordt vergeleken met een kritieke waarde om de nulhypothese te verwerpen of te accepteren.

Stap-voor-stap-instructies

Stap 1: Gegevens voorbereiden

Om de Chi-kwadraattest uit te voeren, heb je eerst de gegevens nodig. Kopieer de omzet van smartphones naar een Excel-werkblad. Zorg ervoor dat je gegevens in een enkele kolom zijn georganiseerd.

Stap 2: Histogram maken

Om eerste visuele indicaties van de verdeling te krijgen, maak je een histogram van je gegevens. Ga naar "Invoegen" en kies "Diagrammen". Voeg een histogram toe door het bereik voor de gegevens te selecteren.

Stap 3: Gefrequenteerde tabel maken

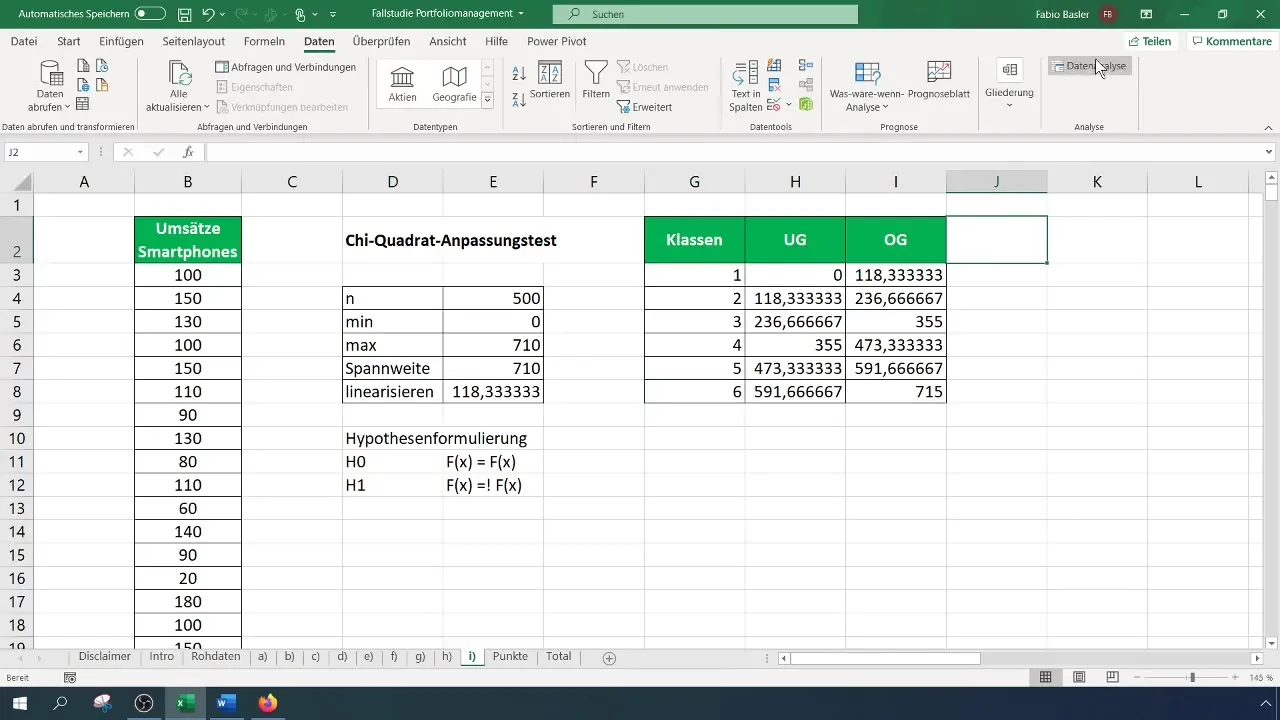
Voor de Chi-kwadraattest heb je een gefrequenteerde tabel nodig. Bepaal eerst het aantal klassen voor je tabel - in dit geval gebruiken we zes klassen. Bereken de breedte van de intervallen en maak de tabel dienovereenkomstig.

Stap 4: Frequenties berekenen

Je moet nu de waargenomen frequenties voor elke klasse berekenen. Ga naar "Gegevensanalyse" in het menu en selecteer "Histogram". Kies het invoergebied voor je gegevens en de klassengrenzen. Bepaal het uitvoergebied voor de frequentietabel.

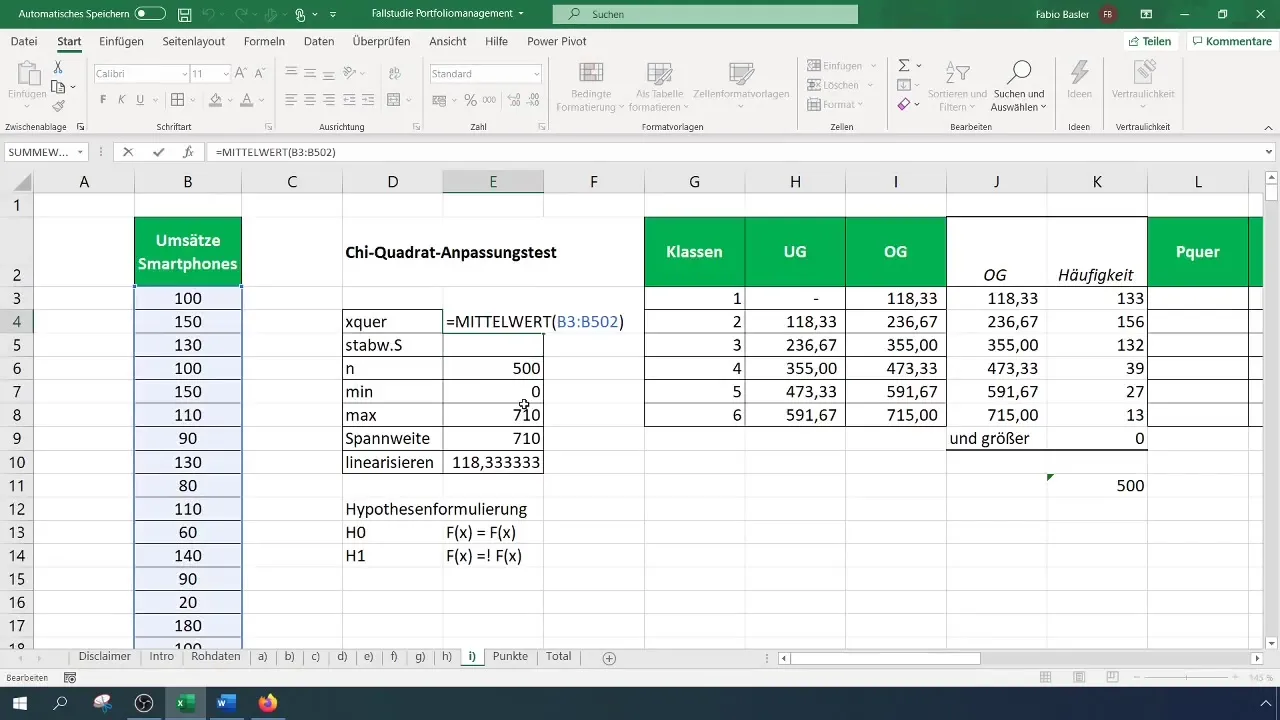
Stap 5: Verwachte frequenties berekenen

Om de verwachte frequenties te berekenen, bereken je de waarschijnlijkheden voor elke klasse op basis van de aangenomen normale verdeling. Hiervoor heb je de gemiddelde waarde en de standaardafwijking van je gegevens nodig.

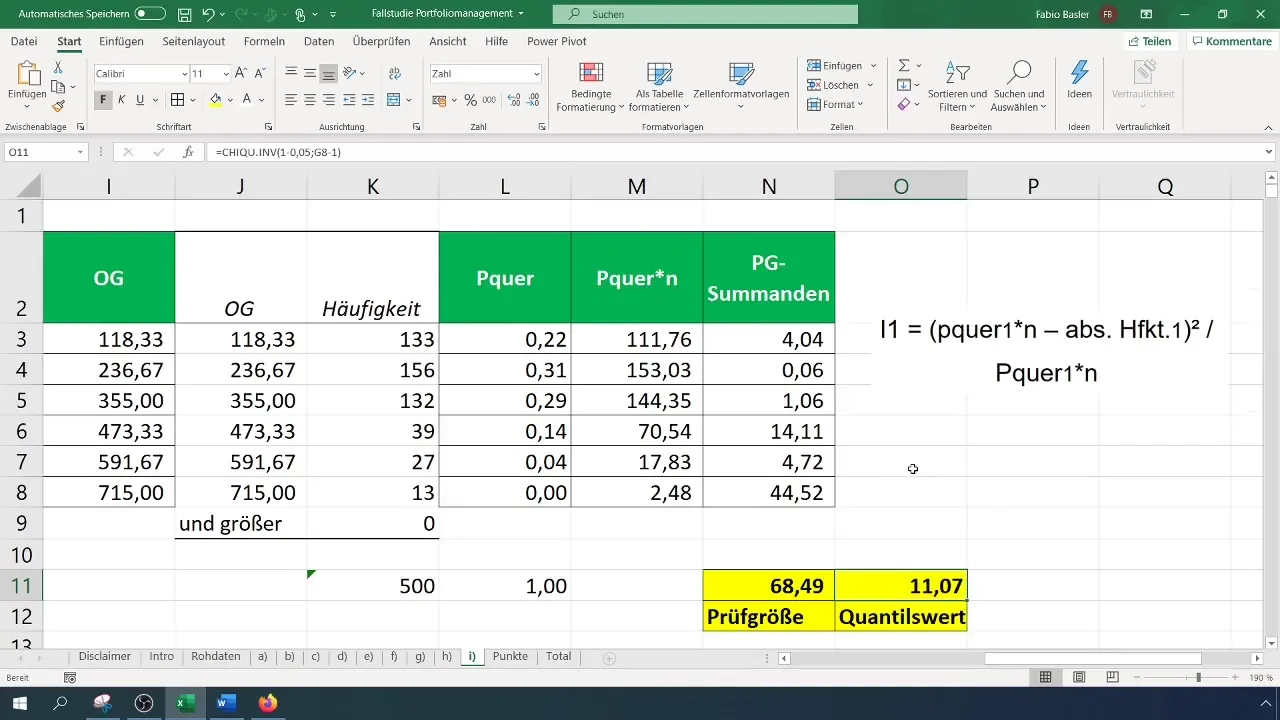
Stap 6: Testingsgrootte berekenen

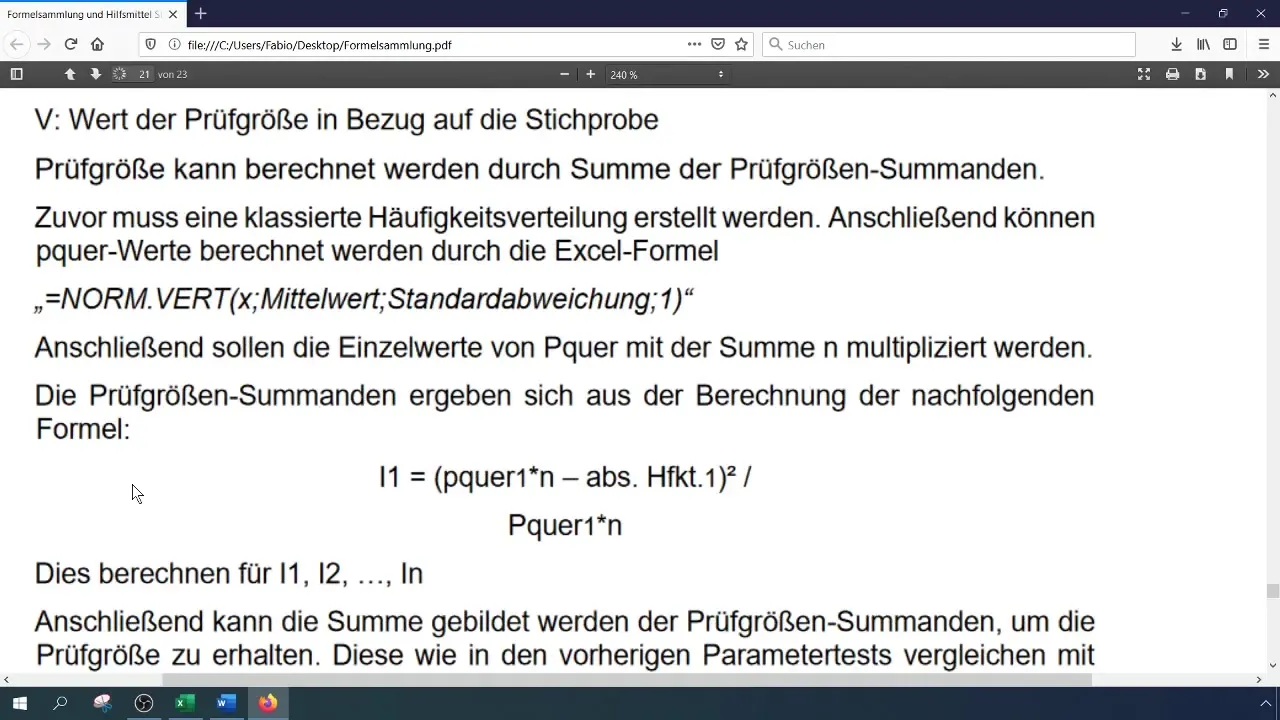
Bereken de testingsgrootte (chi-kwadraat) met de formule:

[ \chi^2 = \sum \frac{(O_i - E_i)^2}{E_i} ]

waarbij (O_i) de waargenomen en (E_i) de verwachte frequenties zijn. Je kunt deze berekening in Excel uitvoeren door de afzonderlijke componenten in aparte cellen op te slaan.

Stap 7: Kritieke waarde berekenen

Om de testingsgrootte te beoordelen, moet je de kritieke waarde (chi-kwadraat) berekenen voor je betrouwbaarheidsniveau en het aantal vrijheidsgraden. Het aantal vrijheidsgraden voor de chi-kwadraattest is (k - 1), waarbij (k) het aantal klassen is.

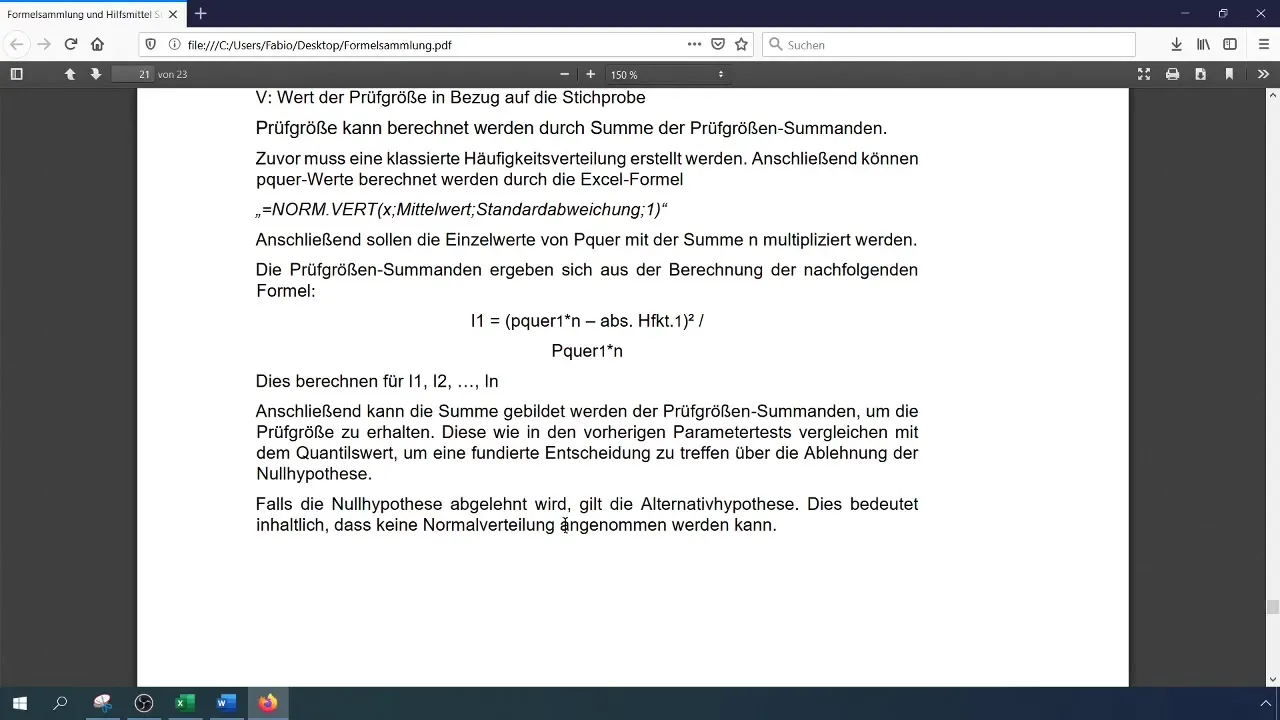
Stap 8: Hypotheses controleren

Vergelijk je berekende testingsgrootte met de kritieke waarde. Als de testingsgrootte groter is dan de kritieke waarde, wijs dan de nulhypothese af, wat betekent dat de gegevens niet normaal verdeeld zijn. Anders accepteer je de nulhypothese.

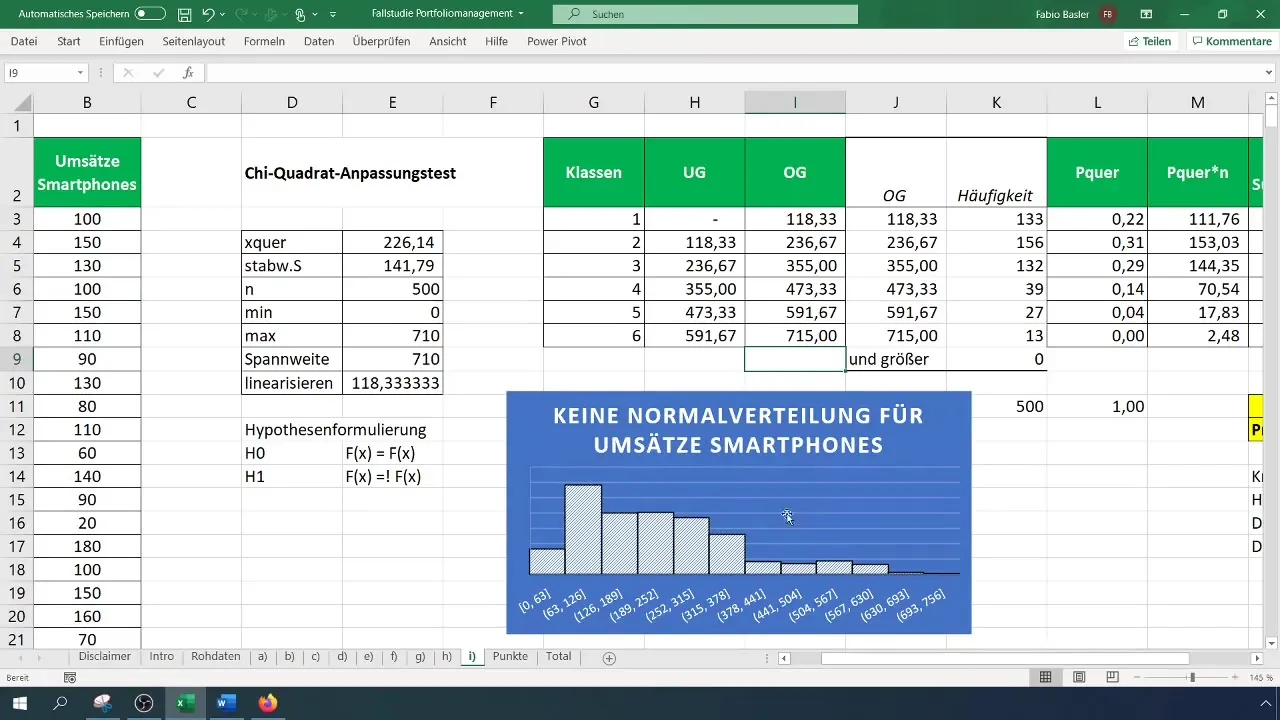
Stap 9: Resultaten samenvatten

Houd je resultaten vast en breid ze uit met grafische gegevens en hypothesetesten. Vergeet niet om je histogram te controleren om visueel te bevestigen dat de verdeling niet normaal is.

Samenvatting

Tijdens deze handleiding heb je geleerd hoe je de chi-kwadraat-aanpassingstest in Excel uitvoert om de normale verdeling van je smartphone-omzet te analyseren. De stappen omvatten het maken van een frequentietabel, berekeningen voor de verwachte frequenties, de teststatistiek en uiteindelijk het vergelijken hiervan met de kritieke waarde.