De verwachtingswaarde testen in Excel

Statistische hypothesetests zijn een belangrijk instrument om beslissingen te nemen op basis van gegevens. In deze tutorial leer je hoe je een 1-steekproeftoets voor het verwachtingswaarde in Excel uitvoert om te bepalen of de gemiddelde omzet van een bedrijf is verbeterd na de invoering van een variabel beloningssysteem. Door het toepassen van deze methode zul je in staat zijn om op data gebaseerde beslissingen te nemen en waardevolle inzichten te krijgen in de prestaties van je bedrijf.

Belangrijkste inzichten

• Je leert hoe je hypothesen formuleert en controleert.
• De toetsing wordt in Excel gedaan met behulp van statistische formules.
• De interpretatie van de resultaten maakt geïnformeerde beslissingen mogelijk over omzetstijgingen.

Stap-voor-stap handleiding

Stap 1: Verzamelen en voorbereiden van de gegevens

Je hebt toegang tot een willekeurige steekproef die gemiddelde wekelijkse omzetten van 100 weken omvat. Deze gegevens vormen de basis voor je test. Begin met het invoeren van de relevante informatie in een Excel werkblad.

Stap 2: Bepalen van de hypothesen

Formuleer de nulhypothese (H0) en de alternatieve hypothese (H1). In jouw geval luidt de nulhypothese dat de gemiddelde omzet gelijk is aan of kleiner is dan €41.000 (m ≤ 41.000). De alternatieve hypothese stelt dat de gemiddelde omzet groter is dan €41.000 (m > 41.000).

Stap 3: Berekening van het gemiddelde en de standaardafwijking

Bereken het gemiddelde van de omzetten uit jouw steekproef door de functie Gemiddelde in Excel toe te passen. Om de standaardafwijking te berekenen, gebruik je de formule STDEV.S, aangezien je in de inductieve statistiek werkt en de vrijheidsgraad met één moet verminderen.

Stap 4: Bepaling van de kritische waarde

Bepaal de kritische waarde door de Excel-functie NORM.INV te gebruiken. Plaats daarbij 1 - α (0,98) in de argumenten. Het significantieniveau voor je test is 2%.

Stap 5: Vergelijking van de toetsingswaarde met de kritische waarde

Vergelijk nu de berekende toetsingswaarde met de kritische z-waarde. Als de toetsingswaarde groter is dan de kritische z-waarde, kun je de nulhypothese verwerpen.

Stap 6: Beslissing over de hypothese

Als de toetsingswaarde boven de kritische waarde ligt, wordt de nulhypothese verworpen, wat betekent dat je kunt aannemen dat de gemiddelde omzet is verbeterd. Documenteer deze beslissing in jouw resultaten.

Stap 7: Interpretatie van de resultaten

De interpretatie van jouw resultaten is cruciaal. Je hebt aangetoond dat het nieuwe gemiddelde op €46.669 ligt, wat hoger is dan de vorige waarde van €41.000. Dit duidt erop dat de omzet is verbeterd na de implementatie van het variabele beloningssysteem en dat er dus een positieve invloed is op de motivatie van medewerkers.

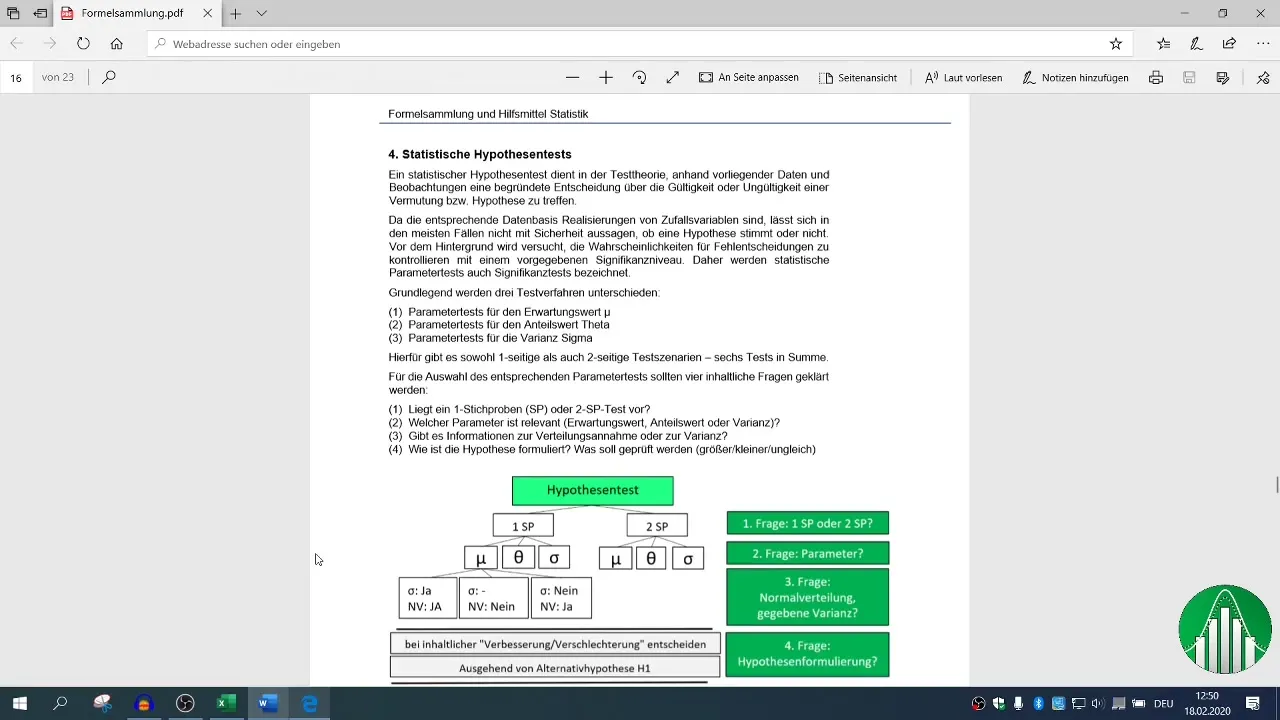
Samenvatting

Je hebt in deze handleiding geleerd hoe je een 1-steekproeftoets voor de verwachtingswaarde in Excel kunt uitvoeren. Van gegevensverzameling en hypothesevorming tot berekening van gemiddelde en standaardafwijking en besluitvorming over de hypothese - elke stap was cruciaal voor de juiste statistische analyse. Met deze kennis kun je gefundeerde beslissingen nemen in jouw bedrijf.