Berekening van het tweezijdige betrouwbaarheidsinterval in Excel

Het is van cruciaal belang om gefundeerde beslissingen te nemen in de bedrijfs- en verkoopomgeving op basis van data-analyses. Een tweezijdig betrouwbaarheidsinterval stelt je in staat om het gebied te bepalen waarbinnen de ware gemiddelde waarde van een parameter met een bepaalde waarschijnlijkheid te vinden is. In deze handleiding laat ik je zien hoe je met behulp van Excel het gebied van de intervalgrenzen voor de wekelijkse omzet van een verkoopsteam kunt berekenen met een betrouwbaarheid van 93%.

Belangrijkste inzichten

Belangrijke aspecten van het tweezijdig betrouwbaarheidsinterval zijn onder andere:

1. De berekening van het gemiddelde als schatting voor de parameter.
2. De bepaling van de standaardafwijking uit de steekproef.
3. Het toepassen van formules om de onder- en bovengrenzen van het interval te berekenen.
4. Het rekening houden met de betrouwbaarheid van de situering van het interval.

Stapsgewijze handleiding

Allereerst moeten we een solide begrip hebben van de begrippen en stappen die dit proces schetsen.

Stap 1: Voorbereiding van gegevens

Allereerst moet je de gegevens voor het verkoopsteam A voorbereiden. Filter de relevante gegevens en kopieer ze naar je Excel-document.

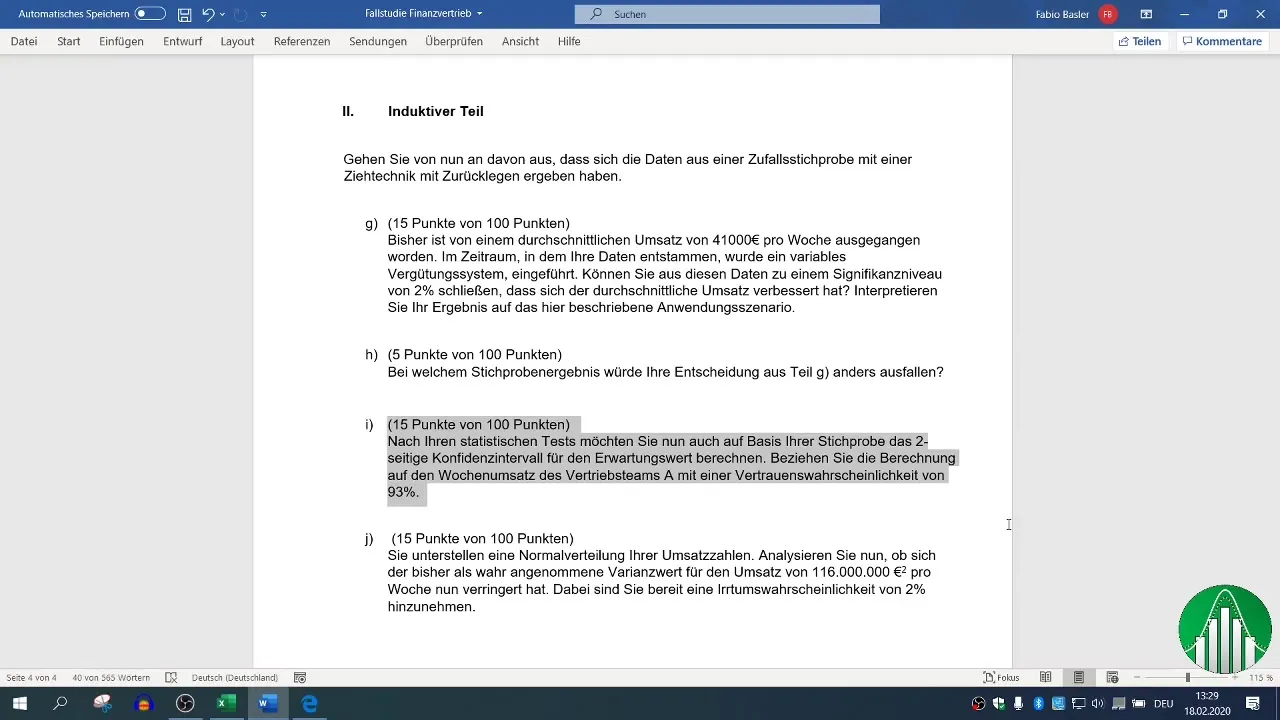
Stap 2: Berekening van het gemiddelde

Om het betrouwbaarheidsinterval te berekenen, is de eerste stap het bepalen van het gemiddelde, dat dient als schatting voor de verwachte omzet. In Excel kun je dit doen met de formule =GEMIDDELDE(Bereik), waarbij "Bereik" de cel(len) zijn die de gegevens voor de wekelijkse omzet van het verkoopsteam A bevatten.

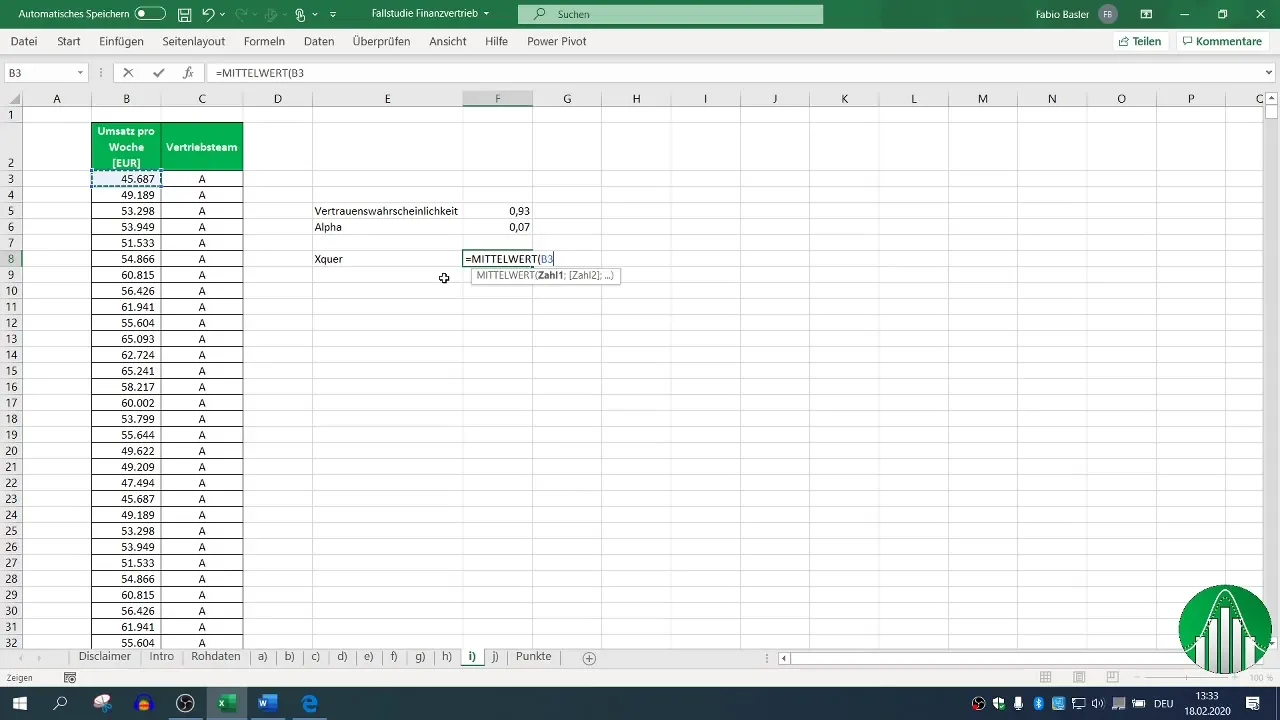
Stap 3: Berekening van de standaardafwijking

De standaardafwijking (σ) is belangrijk voor de berekening van het tweezijdig betrouwbaarheidsinterval. Je kunt dit in Excel berekenen met de formule =STDEVP(Bereik). Zorg ervoor dat je de juiste formule kiest voor de standaardafwijking van de steekproef.

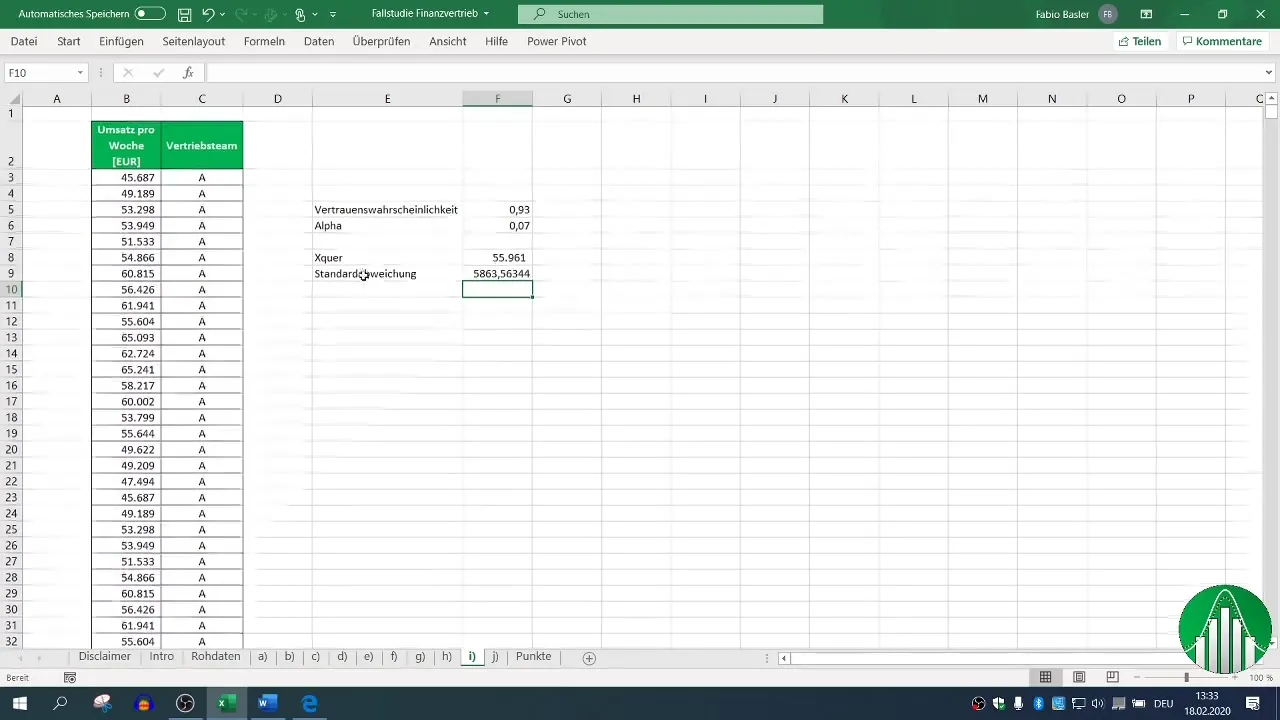
Stap 4: Bepalen van de steekproefomvang

Vervolgens moet je de steekproefomvang (n) bepalen. Tel het aantal datasets dat je voor het verkoopsteam A hebt verzameld bij elkaar op. In dit voorbeeld gaan we uit van 33 datasets.

Stap 5: Berekening van de standaardafwijking van het gemiddelde (σ_m)

Voor de berekening van het betrouwbaarheidsinterval is het noodzakelijk om de standaardafwijking van het gemiddelde te berekenen, wat eenvoudigweg de standaardafwijking gedeeld door de vierkantswortel van de steekproefomvang is.

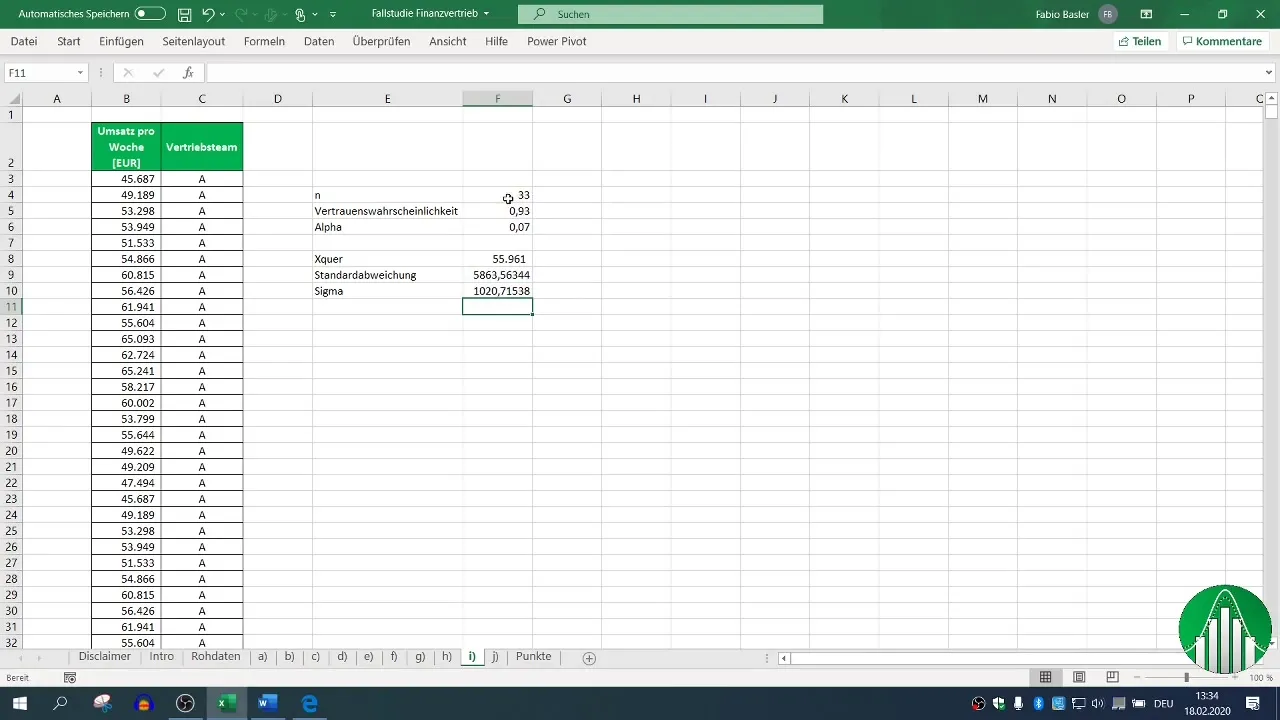
Stap 6: Bepalen van het kwantiel

Voor de berekening van het tweezijdig betrouwbaarheidsinterval heb je het kwantiel nodig. Aangezien je een betrouwbaarheid van 93% opgeeft, is α 7% en vind je de verdeling van het kwantiel door gebruik te maken van de Excel-functie.

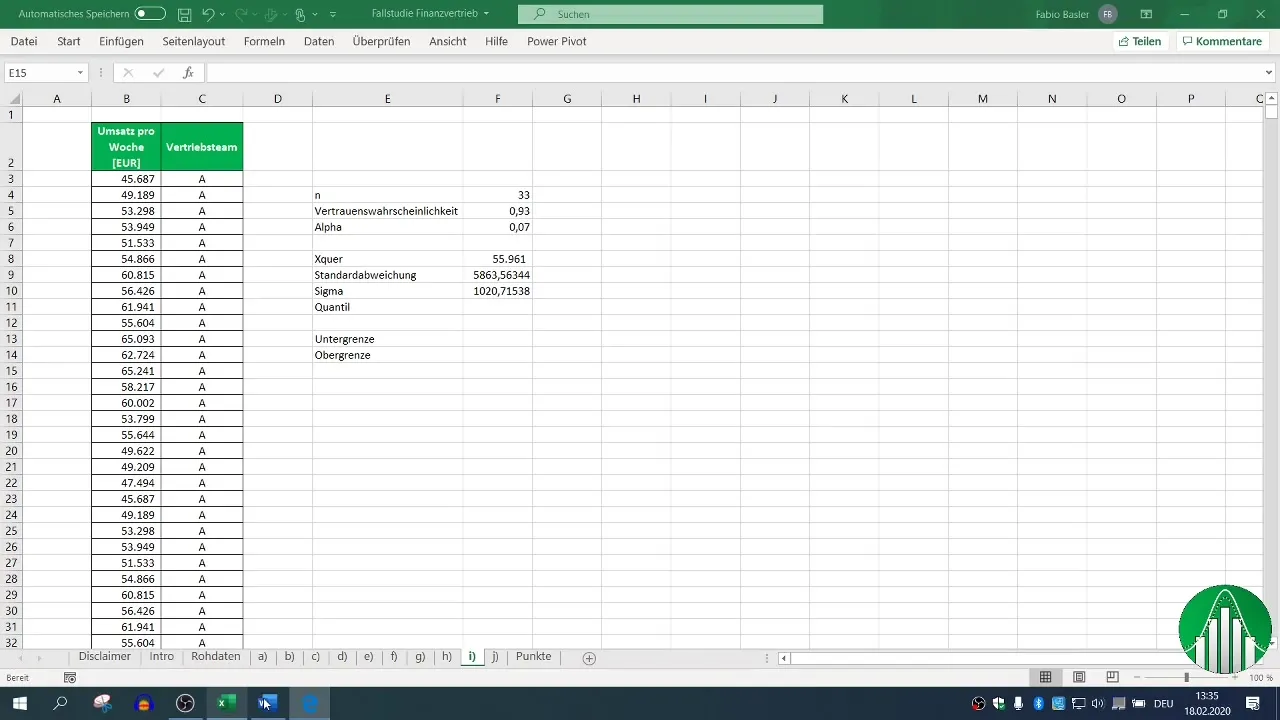
Stap 7: Berekening van de ondergrens

Nu berekenen we de ondergrens van het betrouwbaarheidsinterval. Hiervoor trek je het product van het kwantiel en de standaardafwijking van het gemiddelde af van het gemiddelde (x̄).

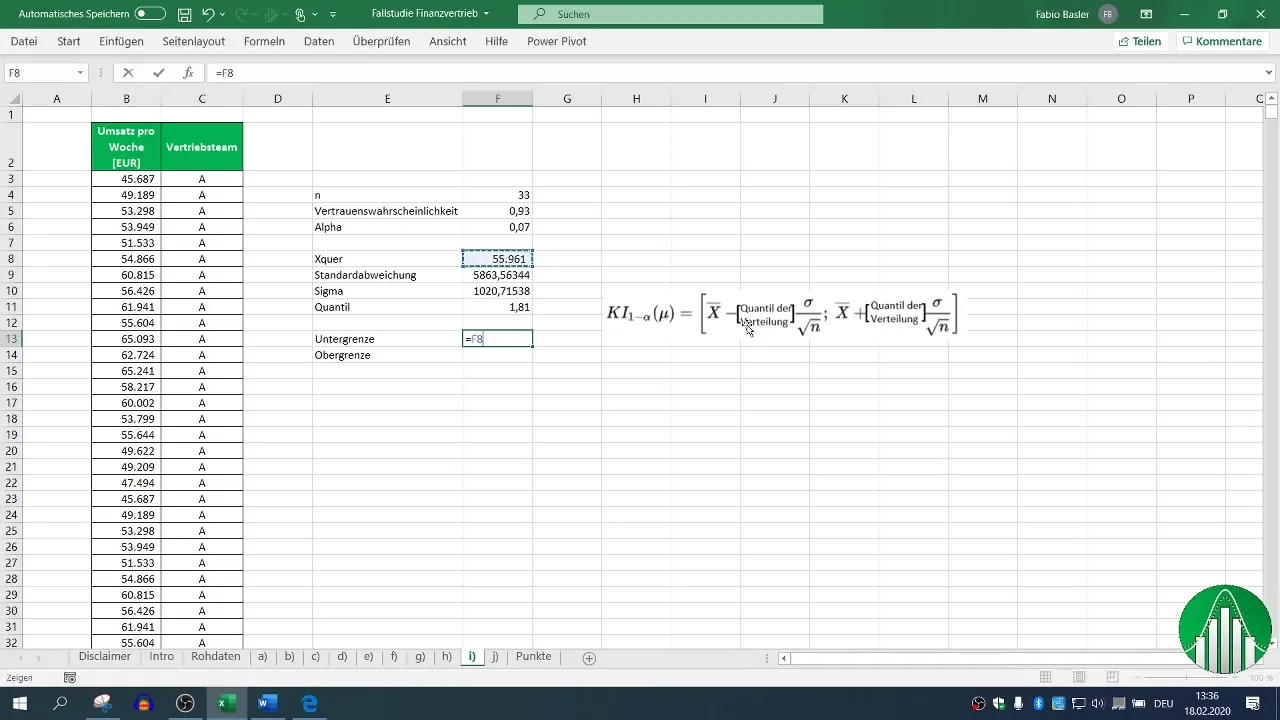
Stap 8: Berekening van de bovengrens

De bovengrens wordt op een vergelijkbare manier berekend, maar je telt het product in plaats van aftrekken.

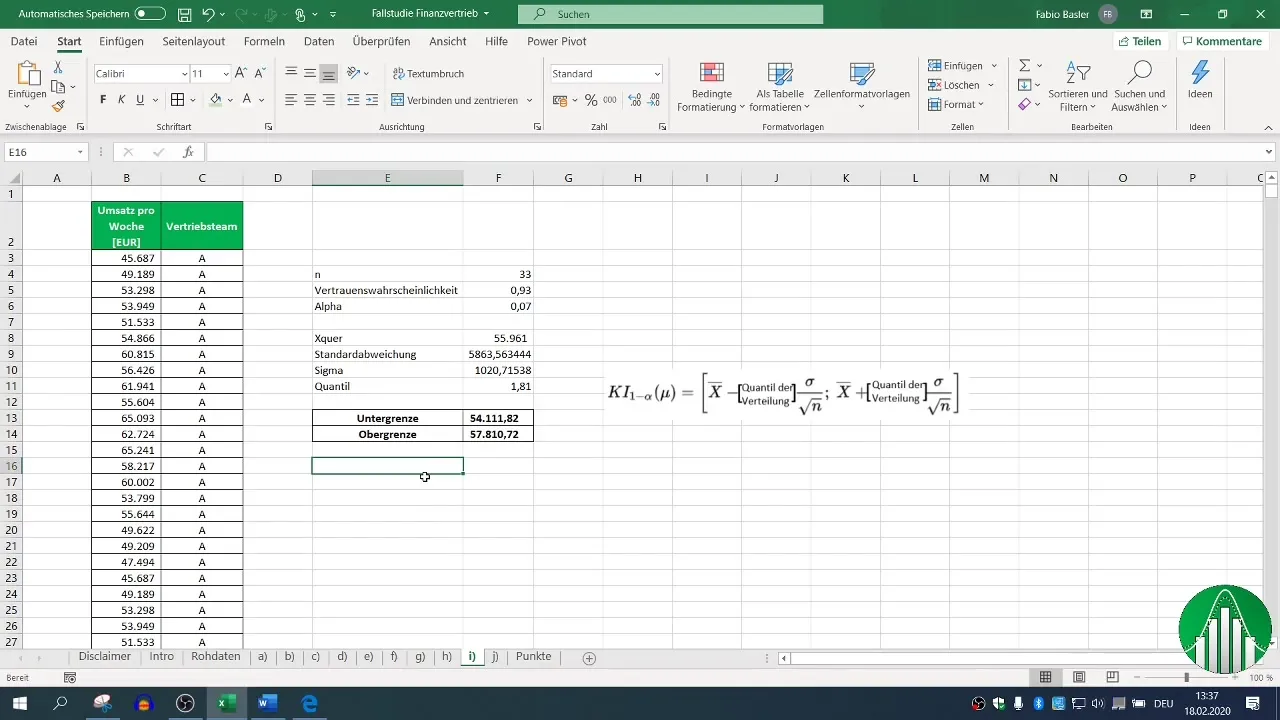
Stap 9: Interpretatie van resultaten

Na deze berekeningen krijg je het tweezijdig betrouwbaarheidsinterval voor de wekelijkse omzet van het verkoopsteam A. In ons voorbeeld ligt het interval tussen 54,111 en 57,810. Dit betekent dat met een betrouwbaarheid van 93% de ware gemiddelde omzetwaarde binnen dit bereik ligt.

Samenvatting

Door de exacte berekening van het tweezijdig betrouwbaarheidsinterval kun je nauwkeurige uitspraken doen over toekomstige omzet. Je hebt geleerd hoe je de relevante gegevens kunt voorbereiden, het gemiddelde en de standaardafwijking kunt berekenen en uiteindelijk de grenzen van het interval kunt bepalen. Met deze methode kun je op data gebaseerde beslissingen nemen in je verkoopgebied.