De mogelijkheid om data-analyse-tools in Excel te gebruiken is essentieel voor succes in business en verkoop. Deze handleiding richt zich op de correlatie- en regressieanalyse om te bepalen hoe het aantal werknemers en het aantal telefoongesprekken de omzetcijfers beïnvloeden. Het uitvoeren van beide analyses helpt je om deze relaties kwantitatief te beoordelen en maakt de interpretatie van de resultaten begrijpelijk.
Belangrijkste inzichten
- Verschil tussen correlatie en regressie: correlatie toont de relatie tussen twee variabelen, terwijl regressie de impact van meerdere onafhankelijke variabelen op een afhankelijke variabele onderzoekt.
- Inzicht in de statistische significantie en kwaliteit van het model.
- Kwantitatieve beoordeling van de relevantie van de regressors.
Stapsgewijze handleiding
1. Voorbereidingen voor de data-analyse
Voordat je met de analyse kunt beginnen, moet je ervoor zorgen dat je gegevens correct zijn opgemaakt in Excel. Importeer de gegevens over omzet, aantal werknemers en telefoongesprekken in een Excel-werkblad. Controleer of alle datasets volledig zijn en of de benodigde variabelen aanwezig zijn.

2. Uitvoering van de correlatieanalyse
Om de correlatie tussen de variabelen omzet, werknemers en telefoongesprekken te analyseren, kun je de correlatiecoëfficiënt berekenen. Hiervoor gebruik je de formule =CORREL() in Excel. Om een overzicht te krijgen van alle variabelen, maak je een correlatiematrix.
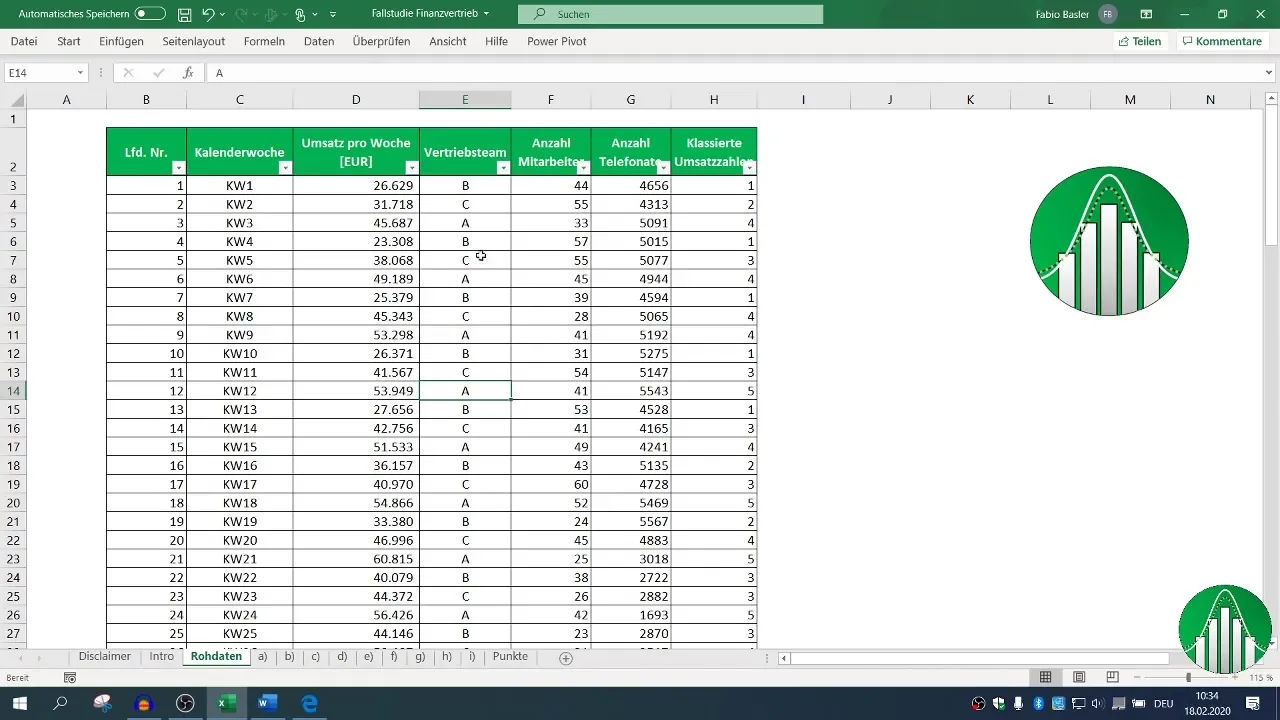
Selecteer eerst de relevante kolommen voor omzet en het aantal werknemers. Met de formule =CORREL( markeer je de gebieden voor omzet en het aantal werknemers. Het resultaat laat zien hoe sterk de relatie is.
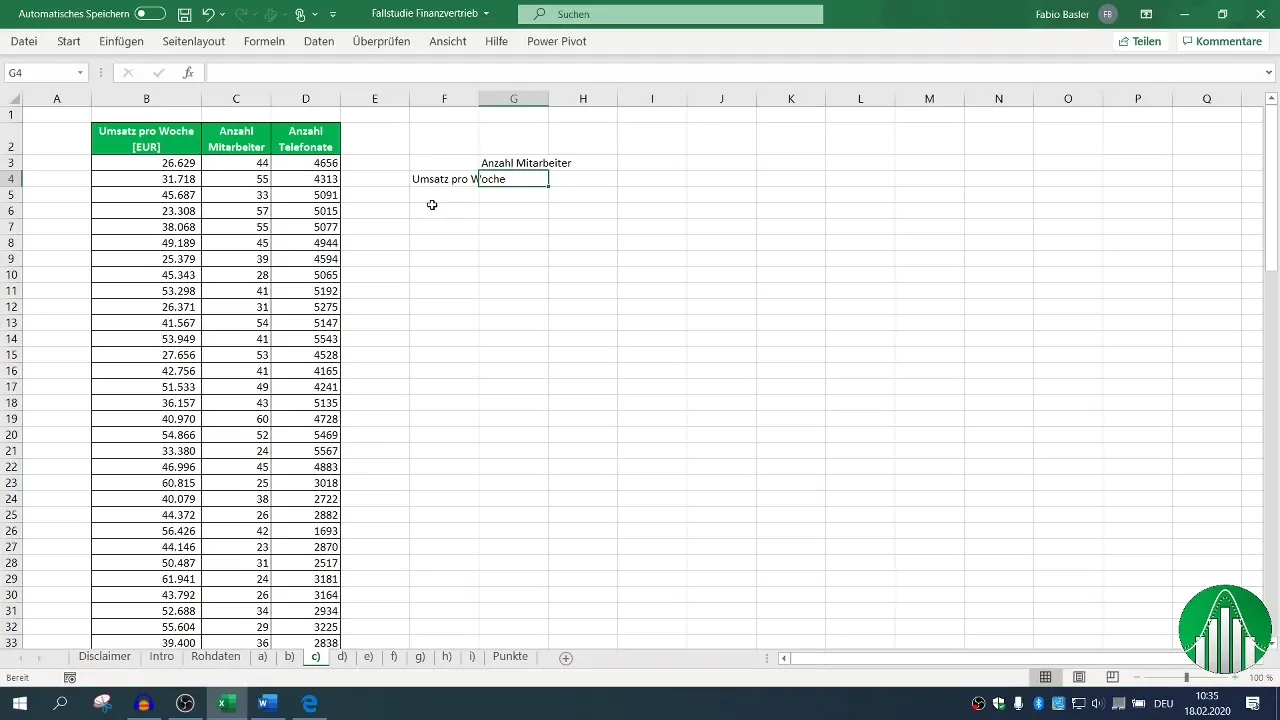
3. Creatie van een correlatiematrix
Voor een meer uitgebreide analyse wordt aanbevolen om de data-analysefuncties van Excel te gebruiken. Activeer de data-analysefunctie als je dit nog niet hebt gedaan. Ga naar het tabblad "Gegevens", klik op "Data-analyse" en kies "Correlatie".
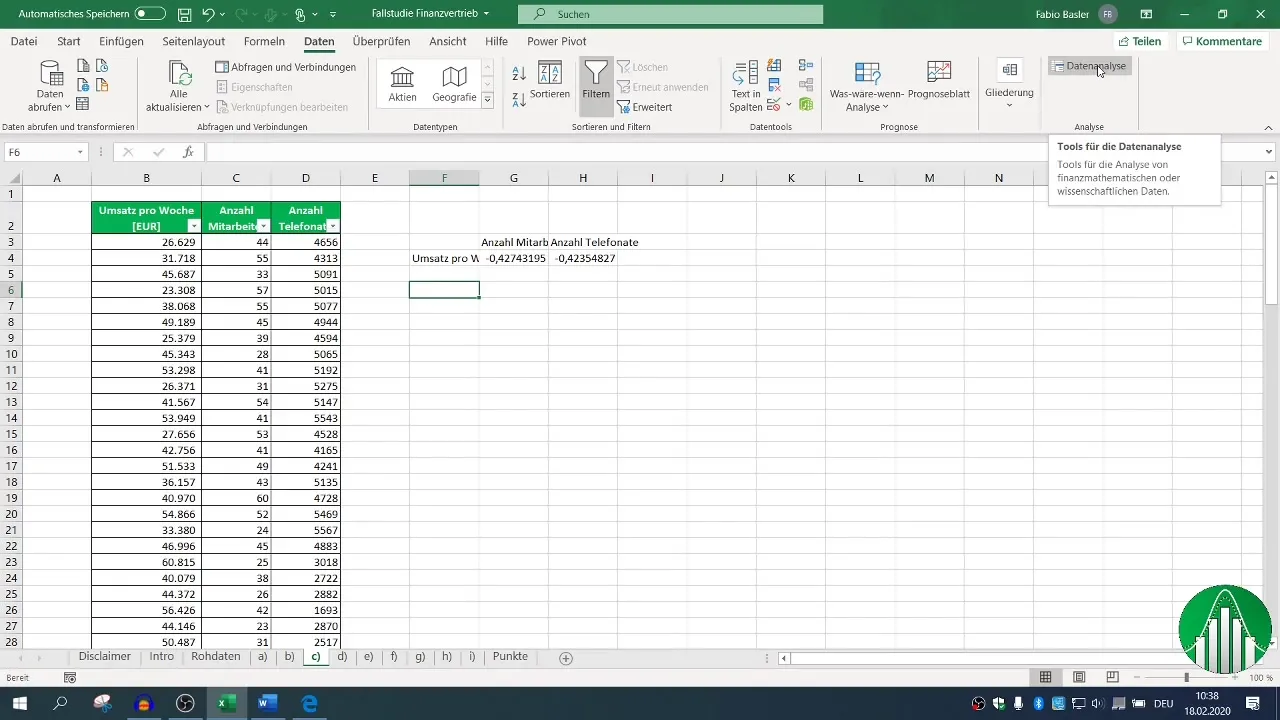
Definieer het invoergebied voor je gegevens en vink het selectievakje "Kopregel" aan zodat Excel de labels correct herkent. Nadat je het uitvoergebied hebt ingesteld, kunt je de correlatiematrix genereren die alle relevante relaties laat zien.
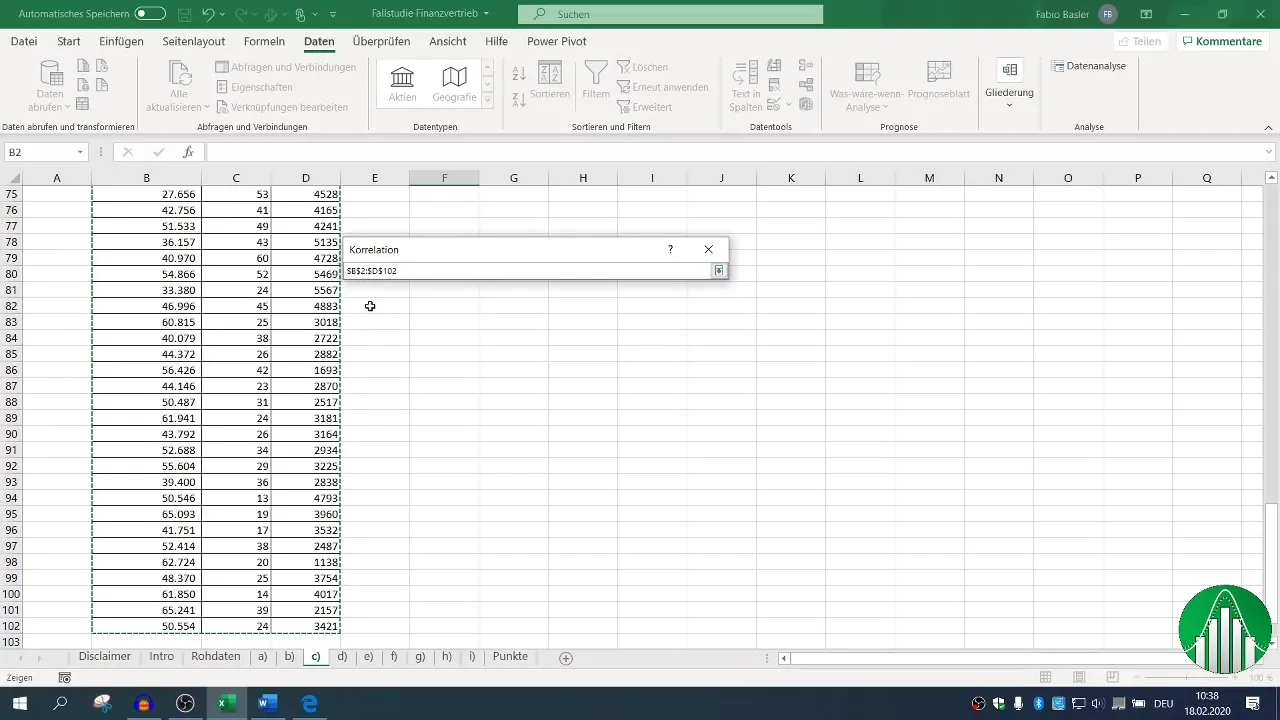
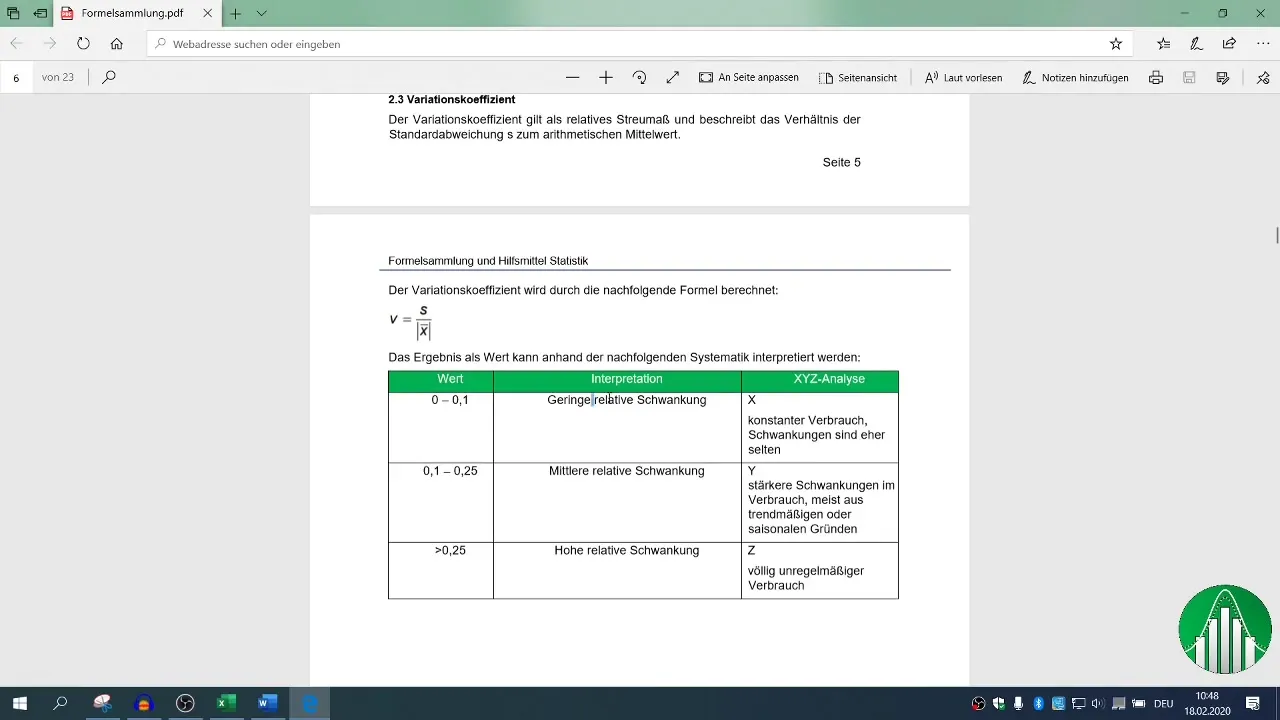
4. Visualisatie van de correlaties
Om de resultaten visueel aantrekkelijker te maken, kan een grafische weergave door een XY-diagram nuttig zijn. Selecteer je X- en Y-gegevens en genereer de puntenwolk.
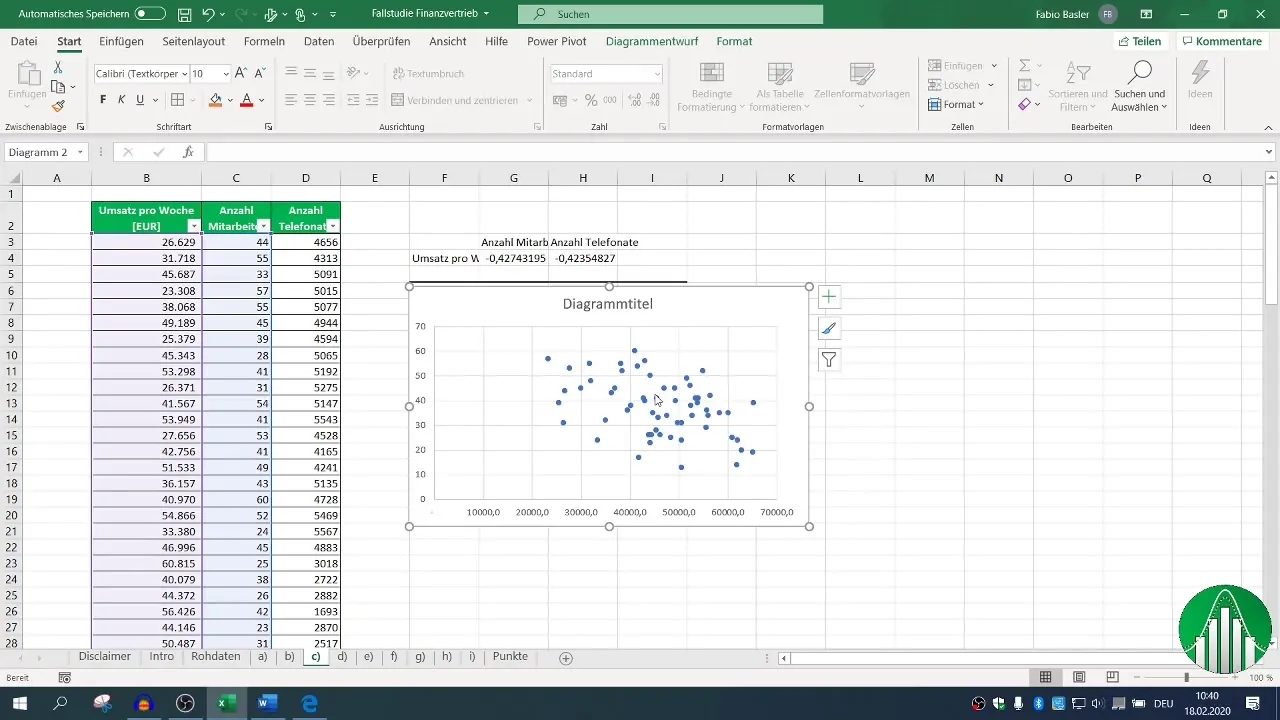
Voeg een trendlijn toe om de relatie visueel weer te geven. Dit kan een intuïtiever inzicht in de gegevens bieden.
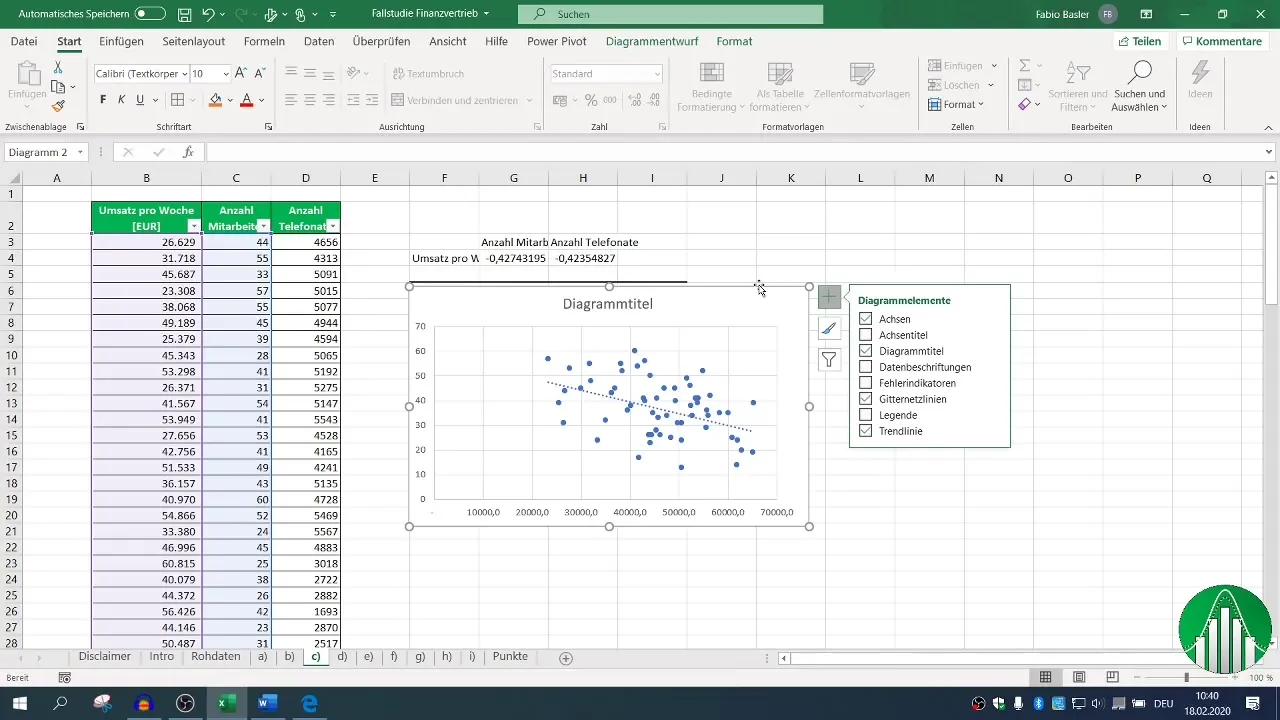
5. Uitvoering van de regressieanalyse
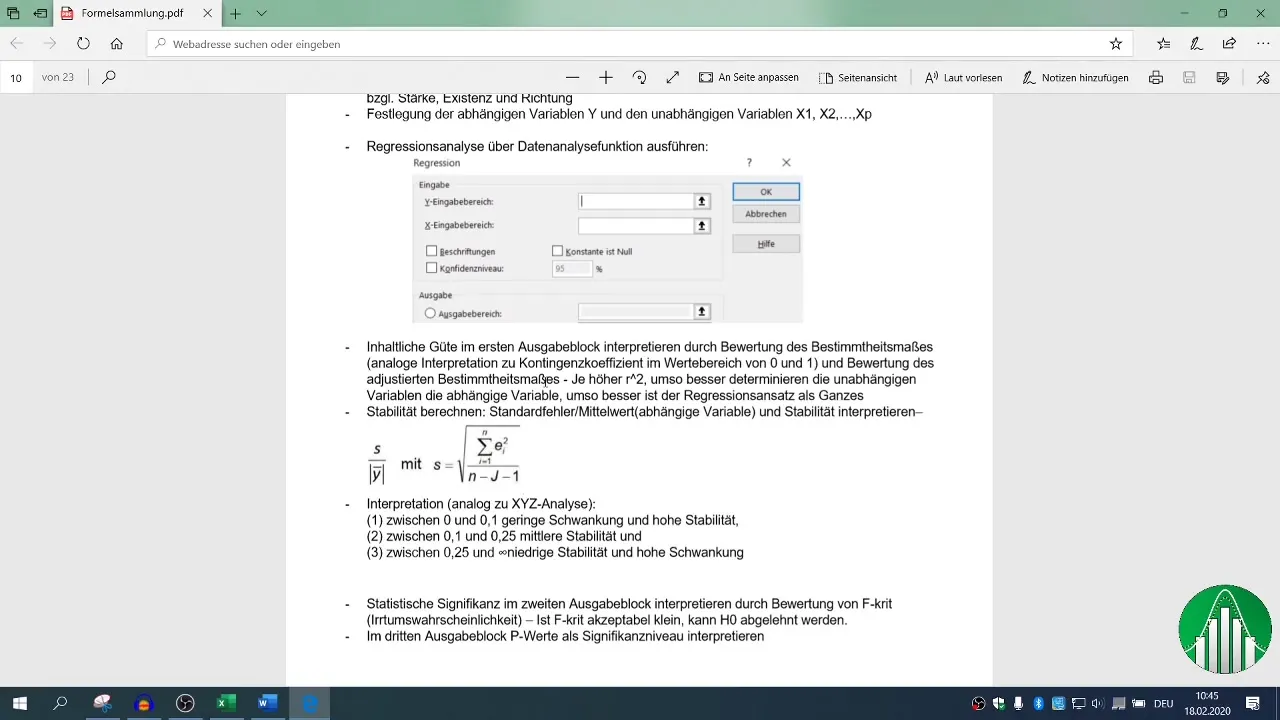
Volg nu de stappen voor de regressieanalyse. Ga opnieuw naar "Gegevens" en kies "Data-analyse", vervolgens "Regressie". Hier kunt je het invoergebied definiëren voor de afhankelijke variabele (omzet) en de onafhankelijke variabelen (aantal werknemers en telefoongesprekken).
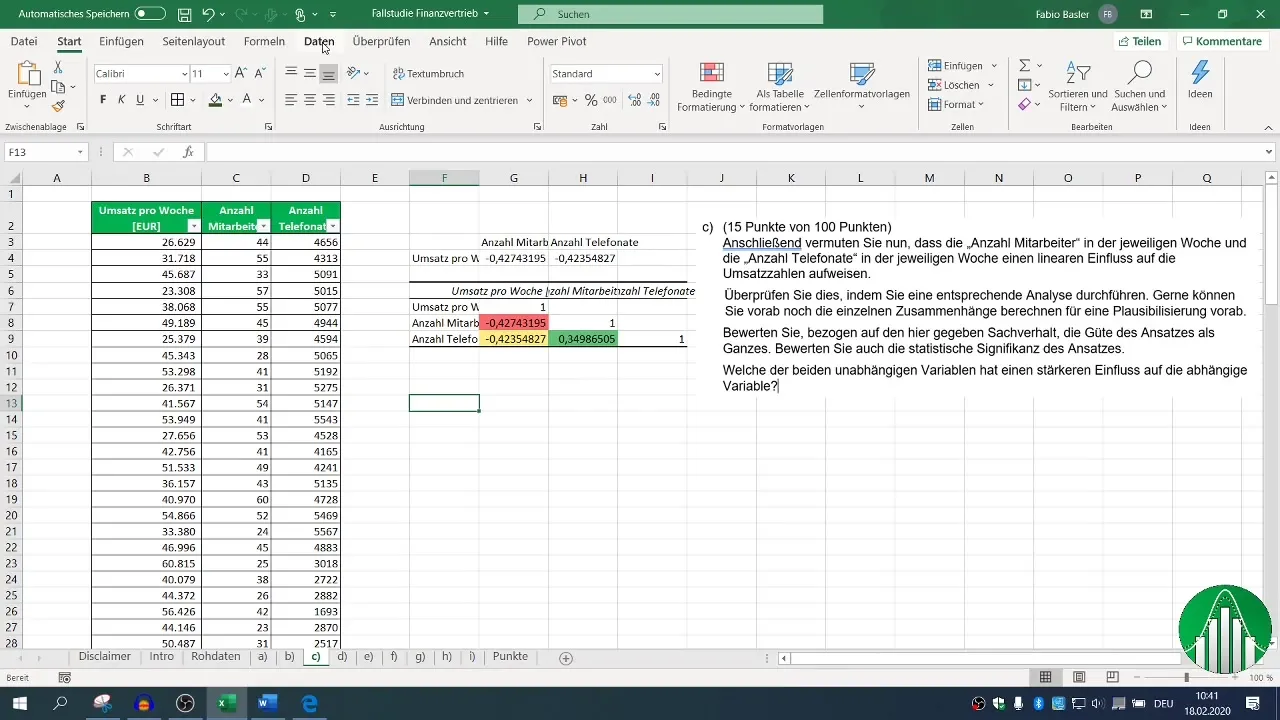
Zorg ervoor dat de kopregel is ingesteld voor de waarden en definieer je uitvoergebied. Het standaardbetrouwbaarheidsniveau is ingesteld op 95%, wat voldoende is voor de meeste analyses.
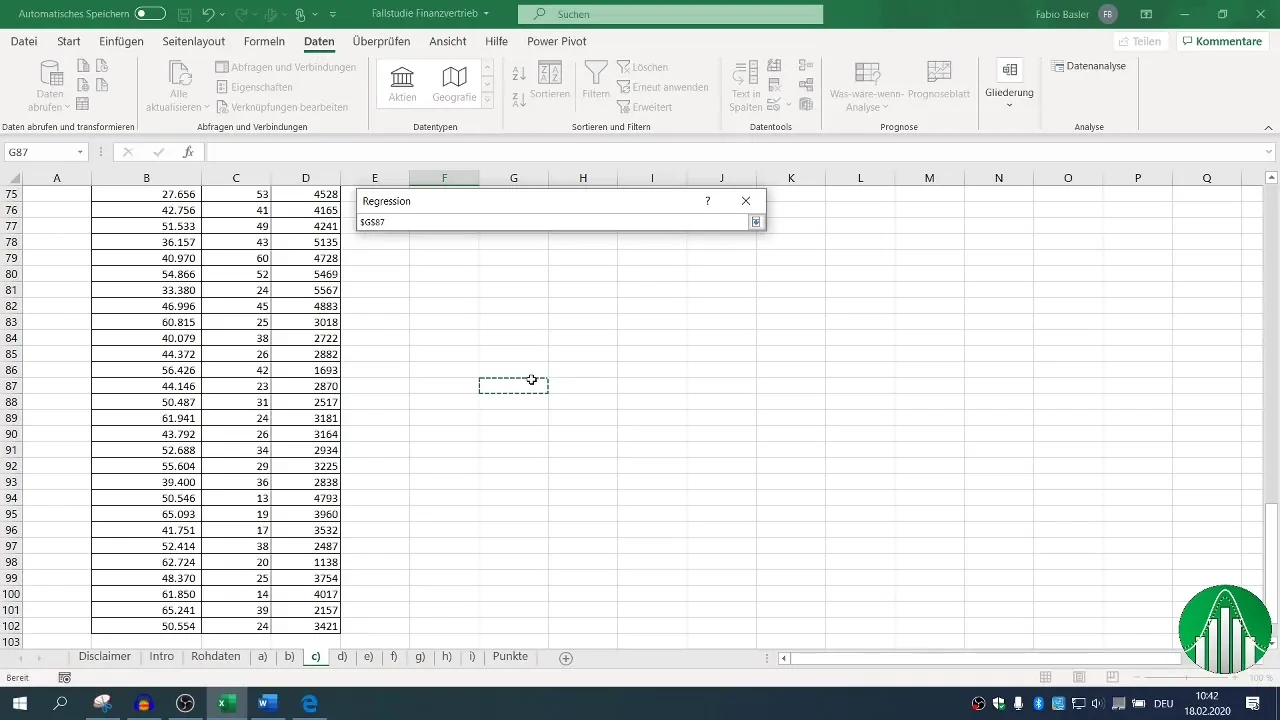
6. Evaluatie van de regressieanalyse
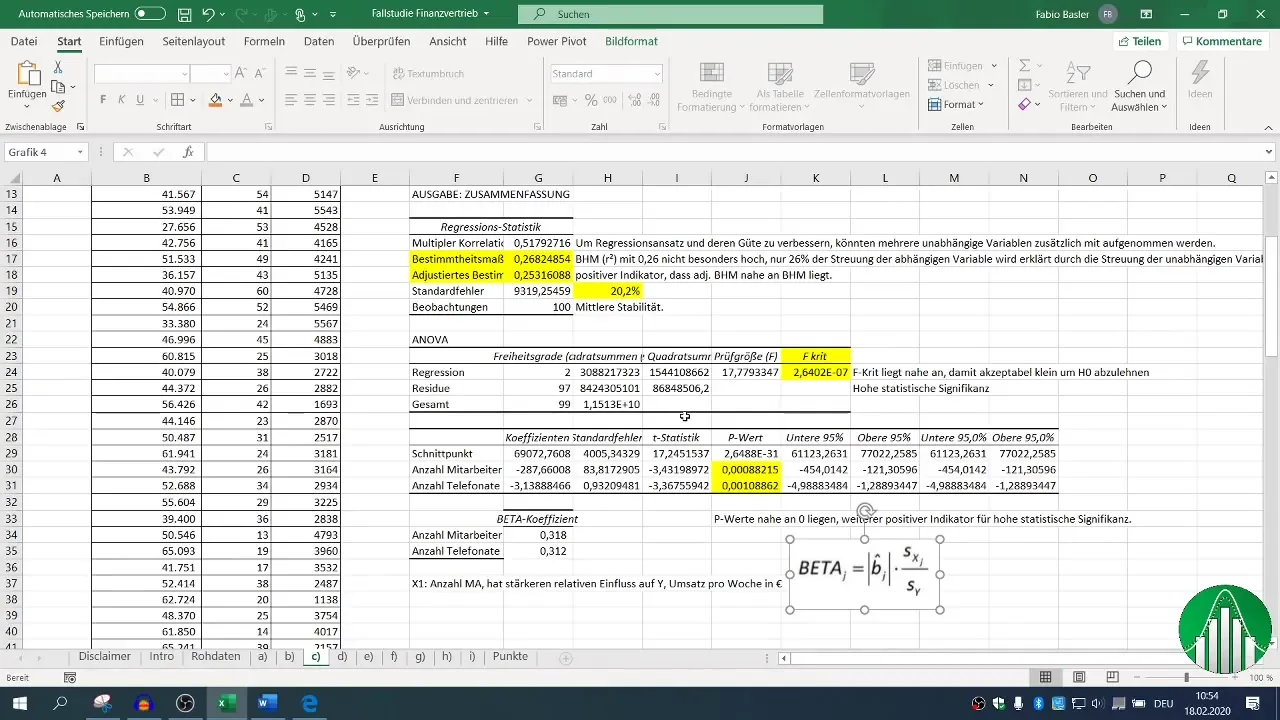
Nadat de regressie is uitgevoerd, heb je verschillende uitvoerblokken tot je beschikking. Richt je op de determinatiecoëfficiënt (R²), die de kwaliteit van het model beschrijft. Een R² van 0,26 geeft aan dat slechts 26% van de variabiliteit in de omzet wordt verklaard door de onafhankelijke variabelen.
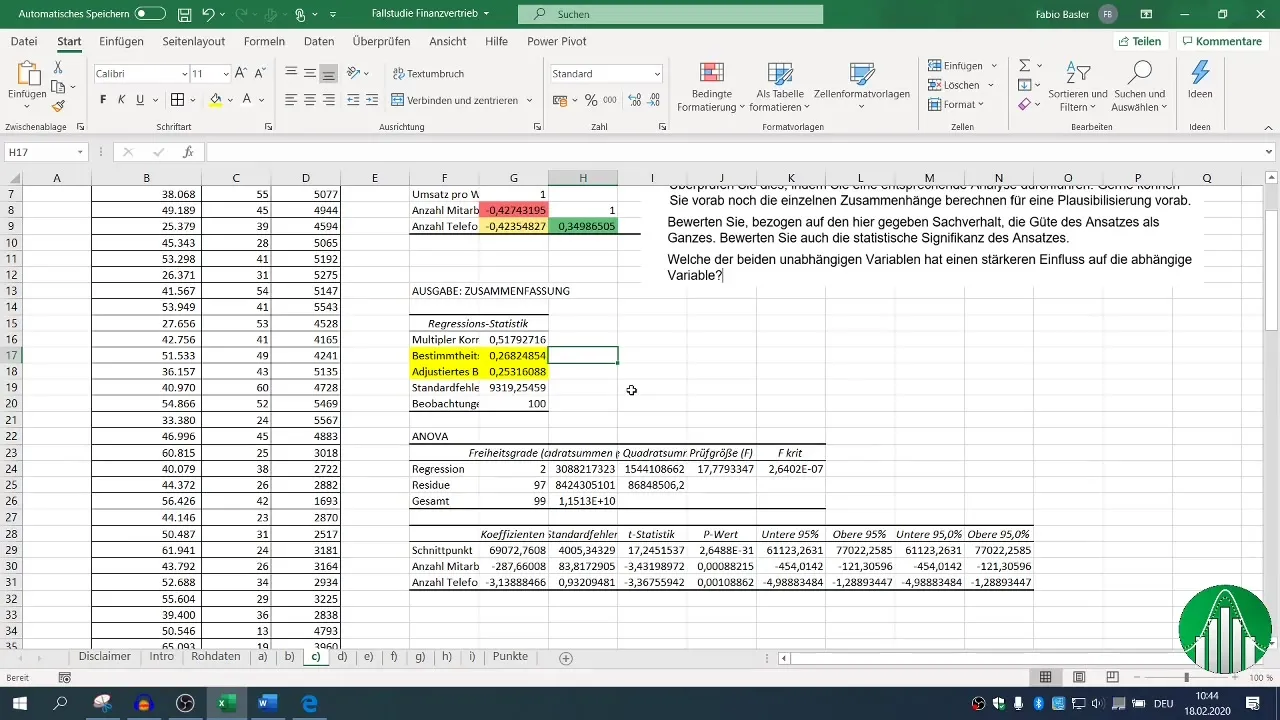
De aangepaste determinatiecoëfficiënt moet dicht bij R² liggen, wat in dit geval een positieve indicator is.
7. Beoordeling van statistische significantie
De F-waarde en de p-waarden van de onafhankelijke variabelen zijn cruciaal om de statistische significantie van je model te beoordelen. Een p-waarde onder 0,05 geeft aan dat de relatie statistisch significant is.
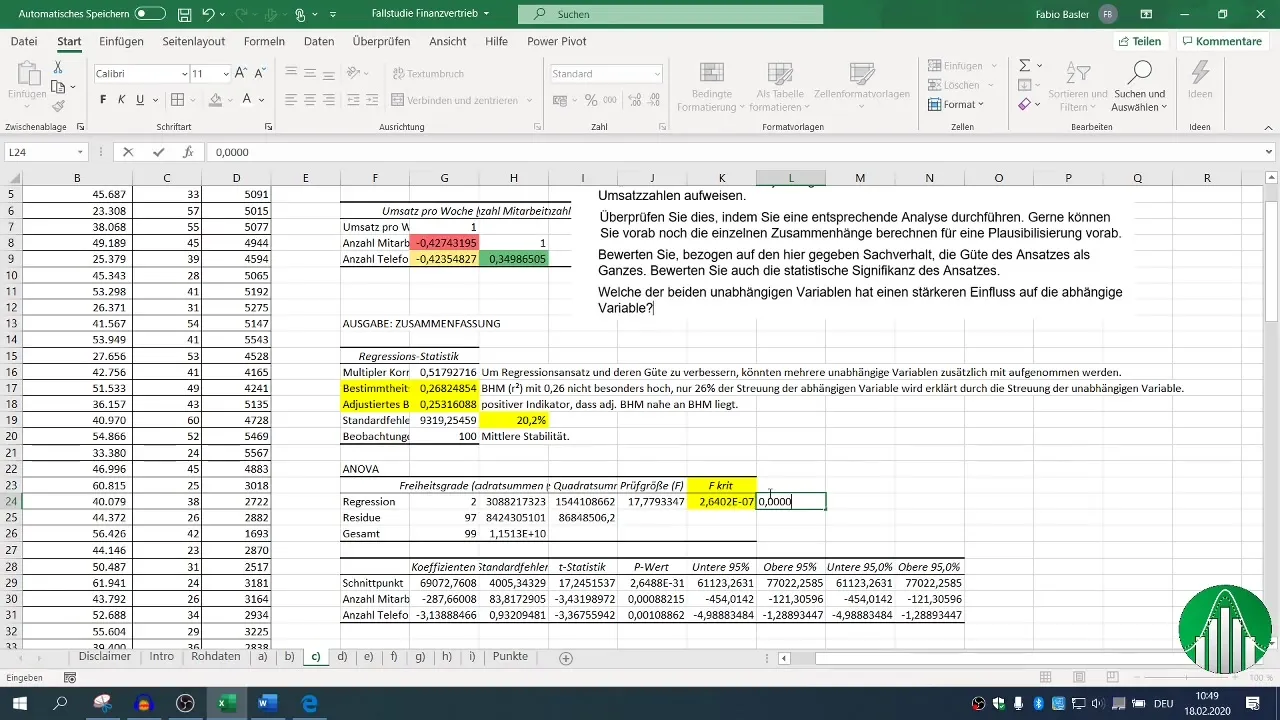
De evaluatie van deze statistische grootheden in verband met R² helpt je om de stabiliteit en de kracht van je resultaten te begrijpen.
8. Vergelijking van beïnvloedende factoren
Uiteindelijk ben je geïnteresseerd in welke factor - aantal werknemers of telefoongesprekken - een grotere invloed heeft op de omzet. Je neemt de bètacoëfficiënten ter hand en vergelijkt ze.
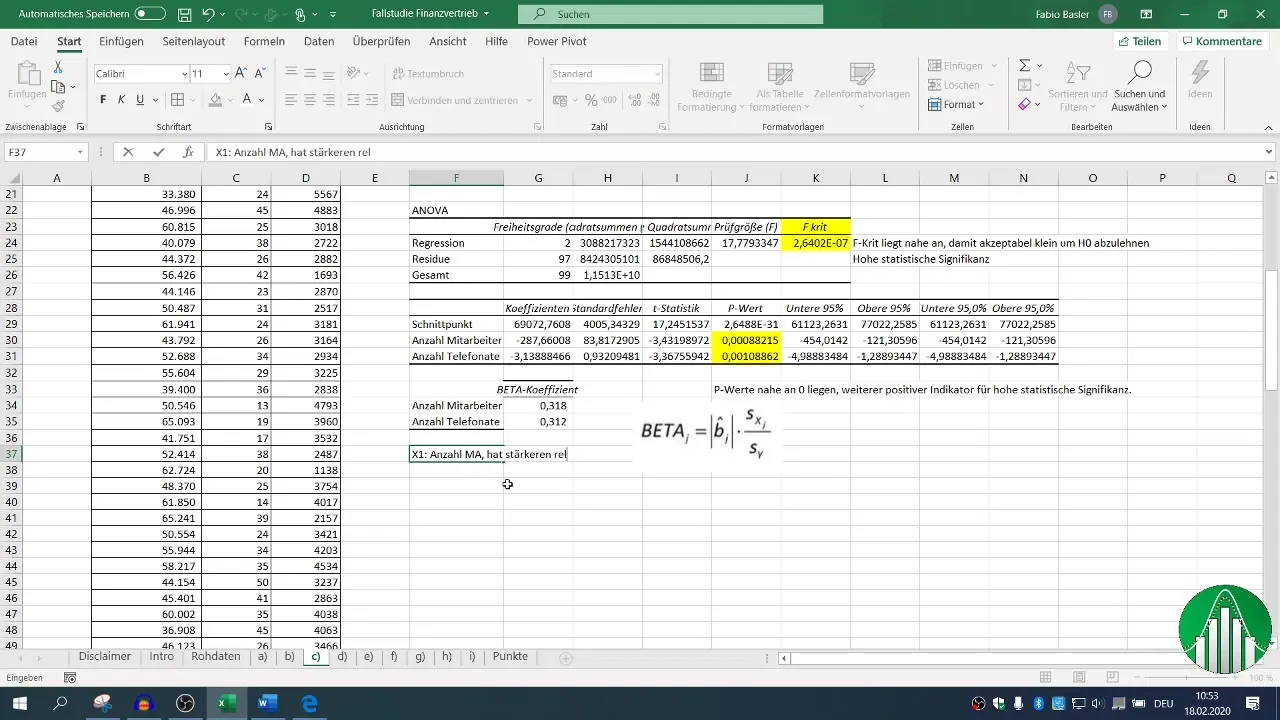
Een hogere bètacoëfficiënt geeft de relatieve invloed aan; het kan blijken dat het aantal werknemers een grotere invloed heeft op de omzet dan het aantal telefoongesprekken.
Samenvatting
De eerdere analyse heeft waardevolle inzichten gegeven in de statistische relaties tussen de variabelen omzet, aantal werknemers en telefoongesprekken. Door systematisch correlatie- en regressieanalyses uit te voeren in Excel, kun je gefundeerde beslissingen nemen op basis van je resultaten.
Veelgestelde vragen
Waarom is een correlatieanalyse belangrijk?Een correlatieanalyse helpt om de relatie tussen twee variabelen te identificeren voordat een gedetailleerde regressieanalyse wordt uitgevoerd.
Hoe interpreteer ik R² in de regressieanalyse?Een R² van 0,26 betekent dat 26% van de schommelingen in de afhankelijke variabele (omzet) worden verklaard door de onafhankelijke variabelen.
Wat is het verschil tussen correlatie en regressie?Correlatie meet de relatie tussen twee variabelen, terwijl regressie de impact van meerdere onafhankelijke variabelen op een afhankelijke variabele beoordeelt.
Hoe kan ik de statistische significantie testen?Je test de statistische significantie aan de hand van de p-waarde; p-waarden onder 0,05 worden als significant beschouwd.
Wat is de rol van de bètacoëfficiënten?De bètacoëfficiënten tonen de relatieve invloed van de onafhankelijke variabelen op de afhankelijke variabele.


