Uitvoeren van een F-toets met twee steekproeven in Excel

Statistische hypothesetoetsen zijn een onmisbaar instrument voor bedrijven om gefundeerde beslissingen te nemen. In het volgende gedeelte laten we je zien hoe je een tweesteekproeven-F-toets in Excel uitvoert om de geldigheid van je hypotheses over de variantie van je omzetgegevens te controleren. Deze handleiding begeleidt je stap voor stap door het proces, zodat je de geleerde technieken veilig kunt toepassen.

Belangrijkste inzichten

• De tweesteekproeven-F-toets wordt gebruikt om de varianties van twee groepen gegevens te vergelijken.
• Het doel is om te controleren of de variantie van de huidige omzetgegevens afwijkt van een aangenomen waarde.
• Excel biedt de tools om de benodigde berekeningen en vergelijkingen uit te voeren.

Stapsgewijze handleiding

1. Gegevensvoorbereiding

Zorg ervoor dat je gegevens klaar zijn voor de test voordat je begint. Verwijder filters om alle relevante gegevens mee te nemen. Selecteer vervolgens de gegevens in de juiste kolommen.

2. Bepaling van de parameters

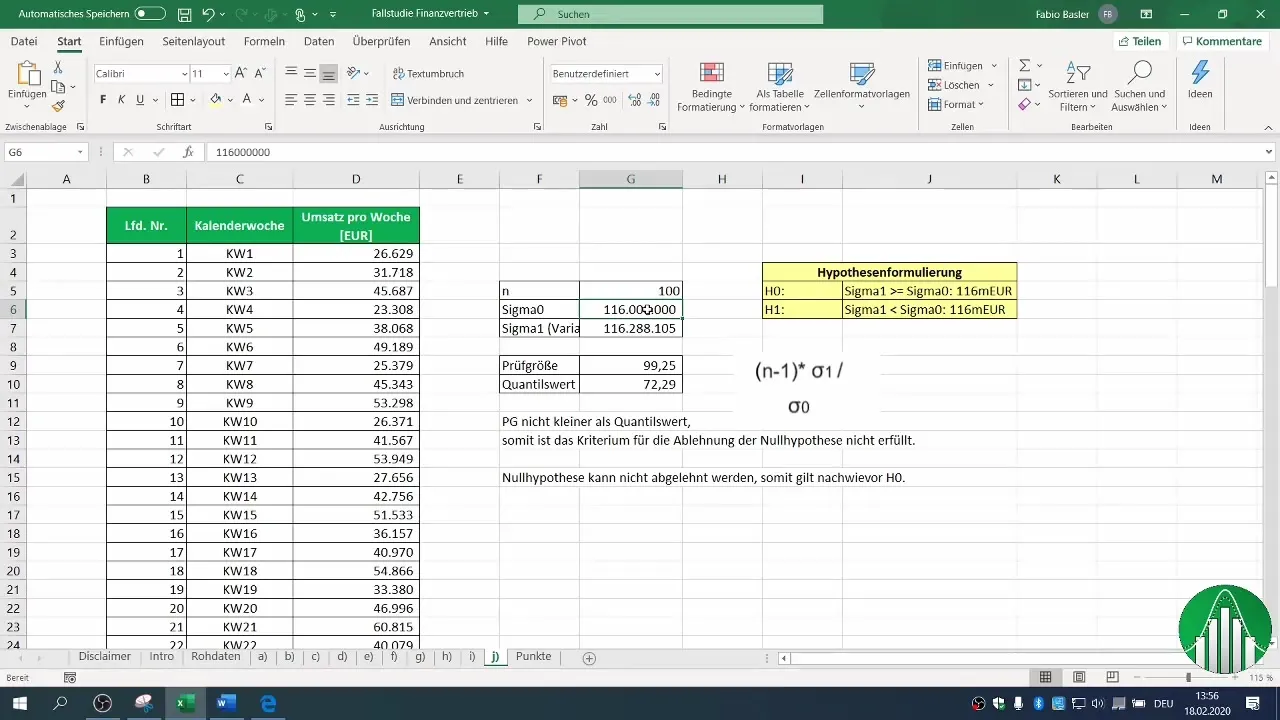
Definieer de parameters voor je test. Je moet weten hoeveel datapunten je analyseert. In ons voorbeeld gaan we ervan uit dat je 100 omzetbedragen hebt die normaal verdeeld zijn.

3. Vastleggen van de eerdere variantiewaarde

De bekende variantie- of omzetwaarde uit het verleden speelt een belangrijke rol in je analyse. In dit voorbeeld is de vroegere waarde 116 miljoen euro per week.

4. Formulering van hypothesen

Formuleer je nulhypothese (H0) en alternatieve hypothese (H1). In dit geval luidt de H0 dat de variantie gelijk blijft of groter is dan 116 miljoen, terwijl de H1 de aanname ondersteunt dat de variantie is afgenomen.

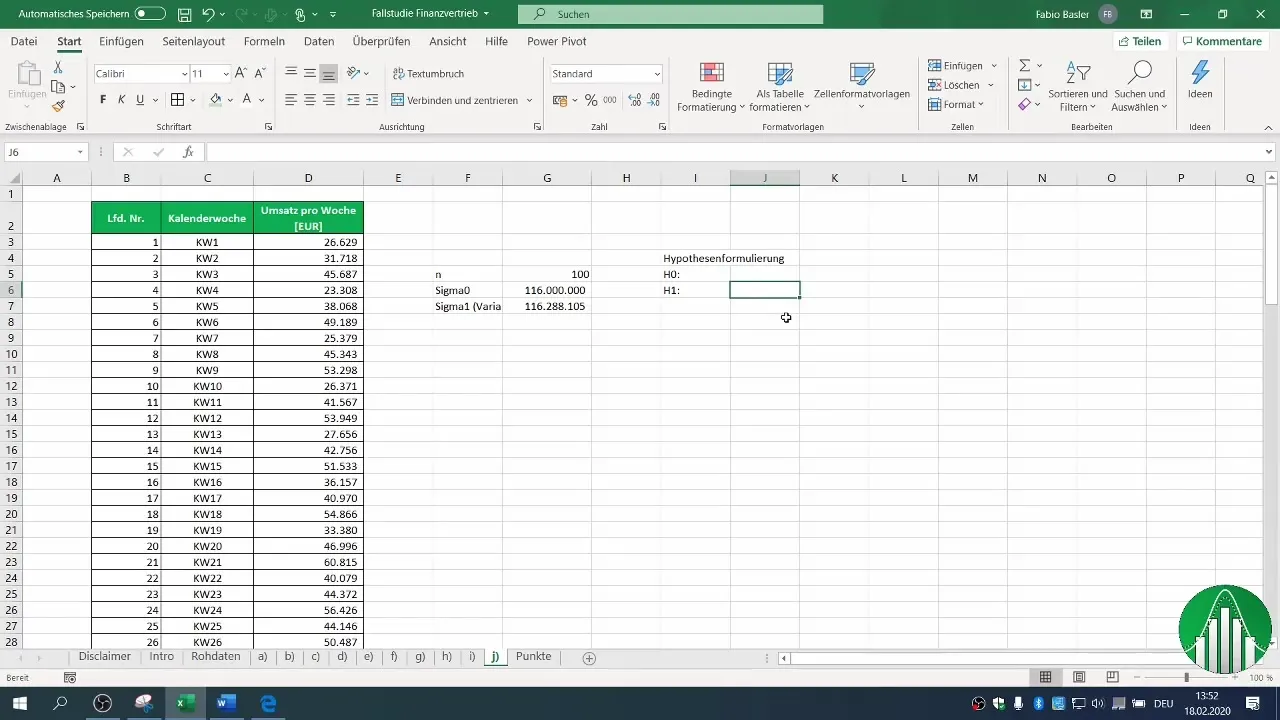
5. Berekening van de toetsingsgrootte

De toetsingsgrootte kan worden berekend aan de hand van de variantie van je steekproef. Voer de noodzakelijke berekeningen uit om de waarde voor je toetsingsgrootte te bepalen. Deze wordt berekend met de formule: (n-1) * σ1 / σ0, waarbij σ1 de variantie van je steekproef is en σ0 de variantie uit het verleden.

6. Bepaling van het kritische gebied

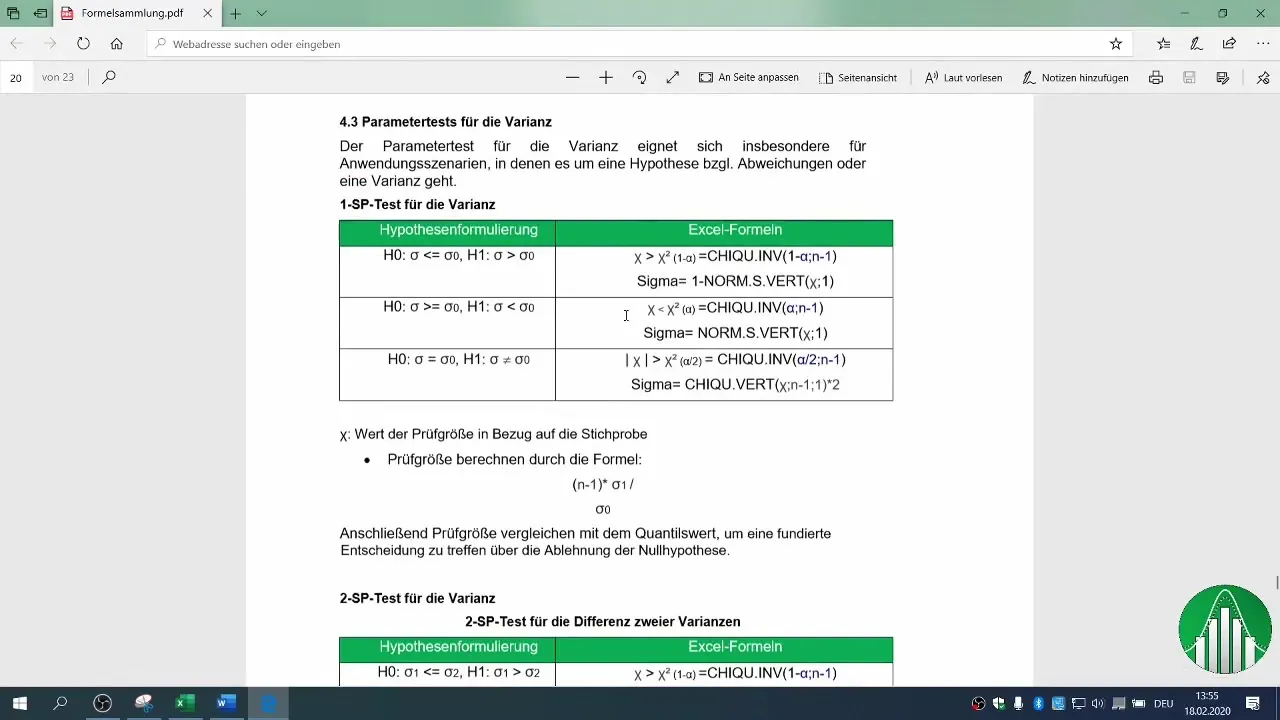
Om te beslissen of je de nulhypothese kunt verwerpen, moet je het kritische gebied bepalen. Gebruik de χ²-verdelingstabel voor je betrouwbaarheidsniveau. In ons voorbeeld hebben we een foutkans van 2% gebruikt.

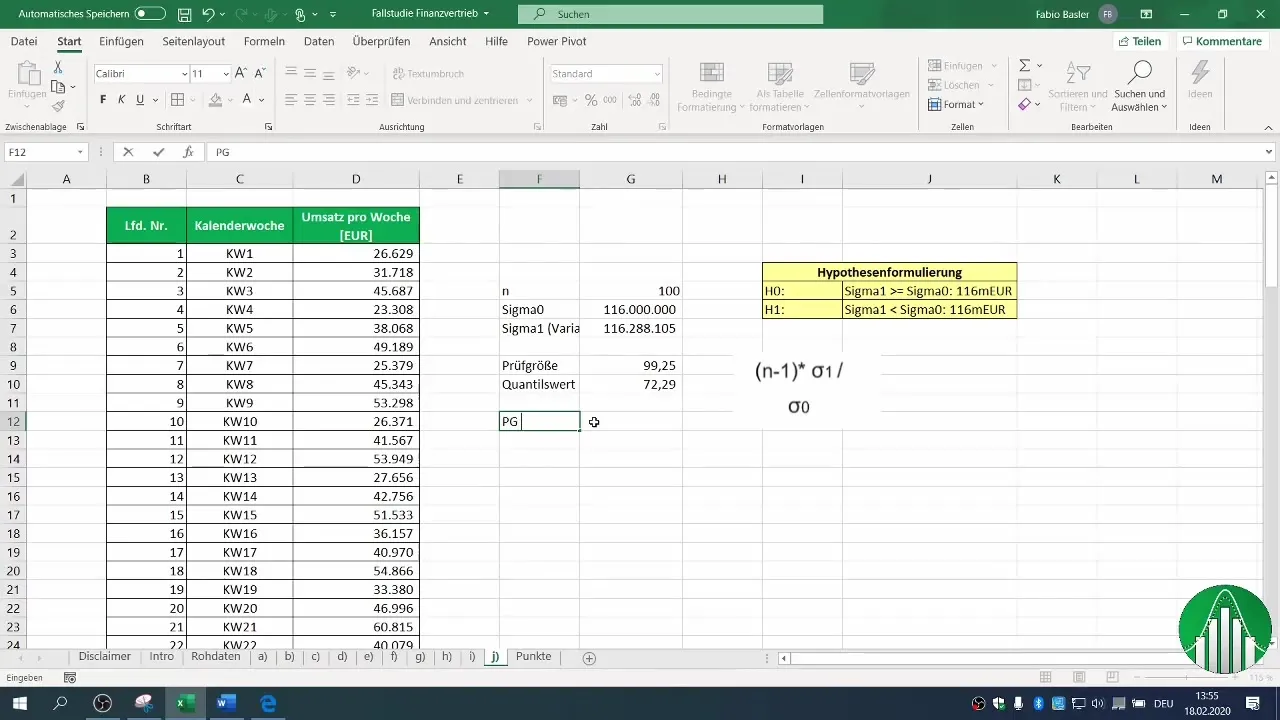
7. Vergelijking van toetsingsgrootte en kritische waarde

Controleer nu of je berekende toetsingsgrootte kleiner is dan de kritische waarde. In dit geval hebben we vastgesteld dat onze toetsingsgrootte niet kleiner is dan de kritische waarde.

8. Trek conclusies

Op basis van je vergelijking kun je nu beslissen of je de nulhypothese kunt verwerpen of niet. In ons voorbeeld hebben we vastgesteld dat de nulhypothese niet kan worden verworpen. Dit duidt erop dat de variantie van je omzetgegevens nog steeds overeenkomt met of zelfs groter is dan de aangenomen waarde.

Samenvatting

In deze handleiding hebben we uitgebreid behandeld hoe je een tweesteekproeven-F-toets in Excel uitvoert. Je hebt geleerd hoe je je gegevens voorbereidt, hypotheses formuleert, de toetsingsgrootte berekent, het kritische gebied bepaalt en tot slot je conclusies trekt. Met deze stappen ben je goed voorbereid om zelfstandig statistische analyses uit te voeren.