Normaalverdeling in Excel - Kansen eenvoudig berekenen

De normale verdeling is een centraal concept in de kansrekening en statistiek. In elke dataset die gelijkmatig verdeeld is, zien we de zogenaamde klokkromme, die vaak voorkomt in enquêtes en verkoopanalyses. In deze tutorial leer je hoe je met Excel de normale verdeling voor een enquête kunt berekenen en visualiseren om belangrijke waarschijnlijkheden te bepalen. Met deze vaardigheden kun je niet alleen je gegevens beter begrijpen, maar ook gericht gebruiken om weloverwogen beslissingen te nemen.

Belangrijkste inzichten

• Je leert de stapsgewijze berekening van de normale verdeling in Excel.
• De mogelijkheden voor grafische weergave van een normale verdeling worden getoond.
• Je begrijpt hoe waarschijnlijkheden voor specifieke gebeurtenissen kunnen worden berekend.

Stapsgewijze handleiding

Zorg er eerst voor dat alle benodigde gegevens in een Excel-tabel klaarstaan. Deze gegevens vertegenwoordigen bijvoorbeeld de omzet uit een enquête.

Visualisatie van de normale verdeling

Om de normale verdeling van de omzet grafisch weer te geven, ga je als volgt te werk:

Selecteer eerst de omzetgegevens in je Excel-tabel en kopieer ze naar een nieuwe kolom. Klik in de menubalk op "Invoegen" en kies "Diagram". Kies hier voor een histogram om de verdeling visueel weer te geven. Je kunt een leeg histogram selecteren om de standaardwaarden van je gegevens weer te geven.

Klik met de rechtermuisknop op het diagram en kies "Gegevens selecteren". Voeg in het geopende venster je omzetgegevens toe als eerste dataset. Selecteer alle datasets in de rijwaarden door de Shift-toets ingedrukt te houden en de waarden te selecteren.

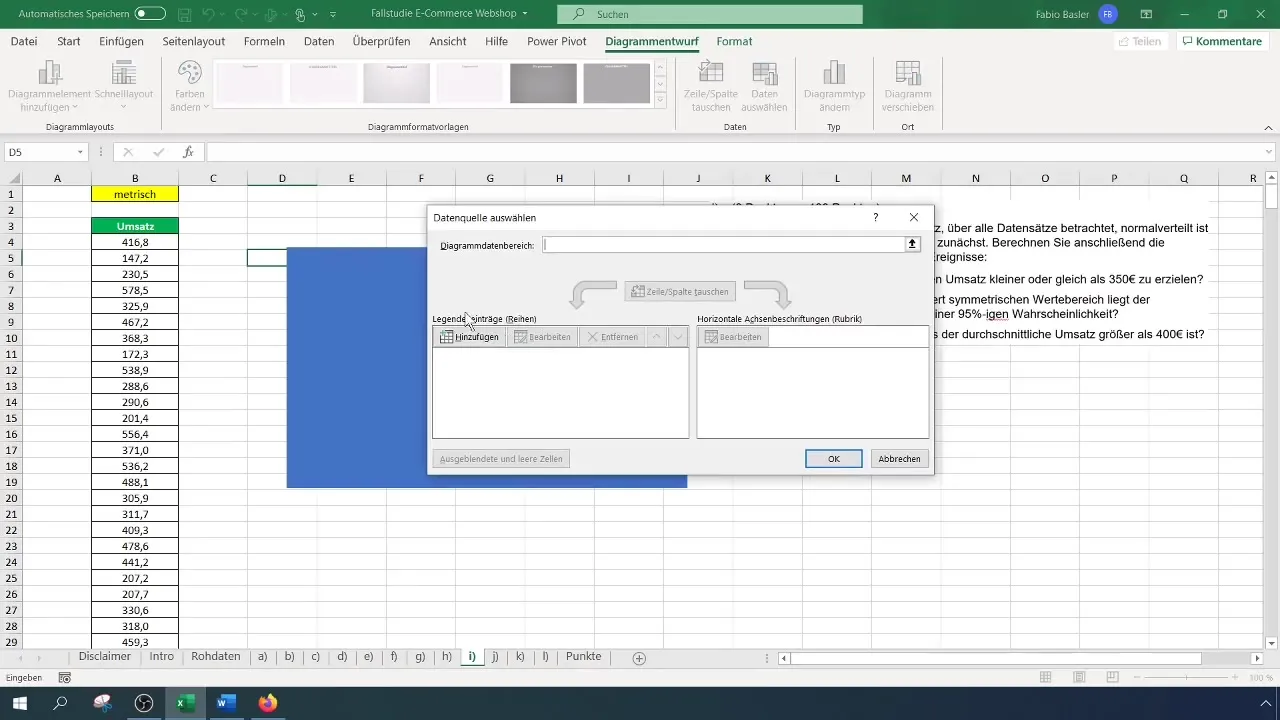
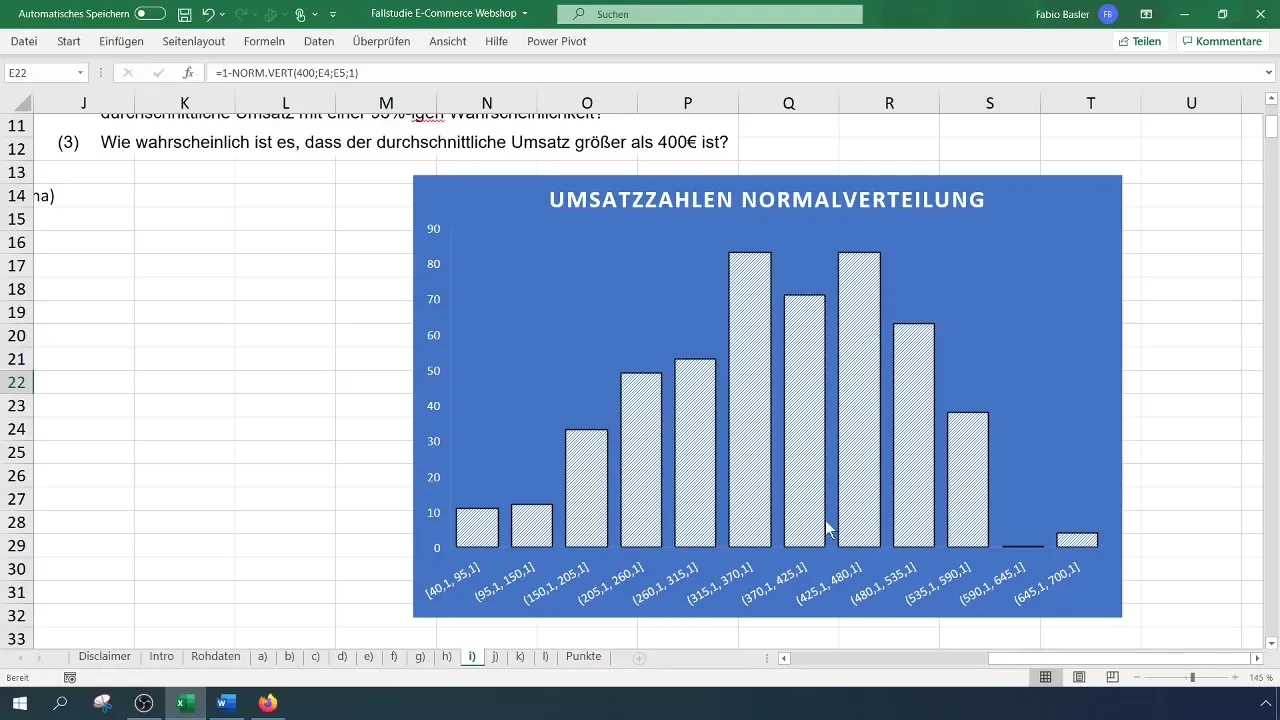
Zodra de gegevens in het histogram worden weergegeven, kun je de titel van het diagram aanpassen om het representatiever te maken. Bijvoorbeeld, verander de titel in "Omzetwaarden normale verdeling". Zorg ervoor dat de klokkromme zichtbaar is; dit duidt op een normale verdeling.

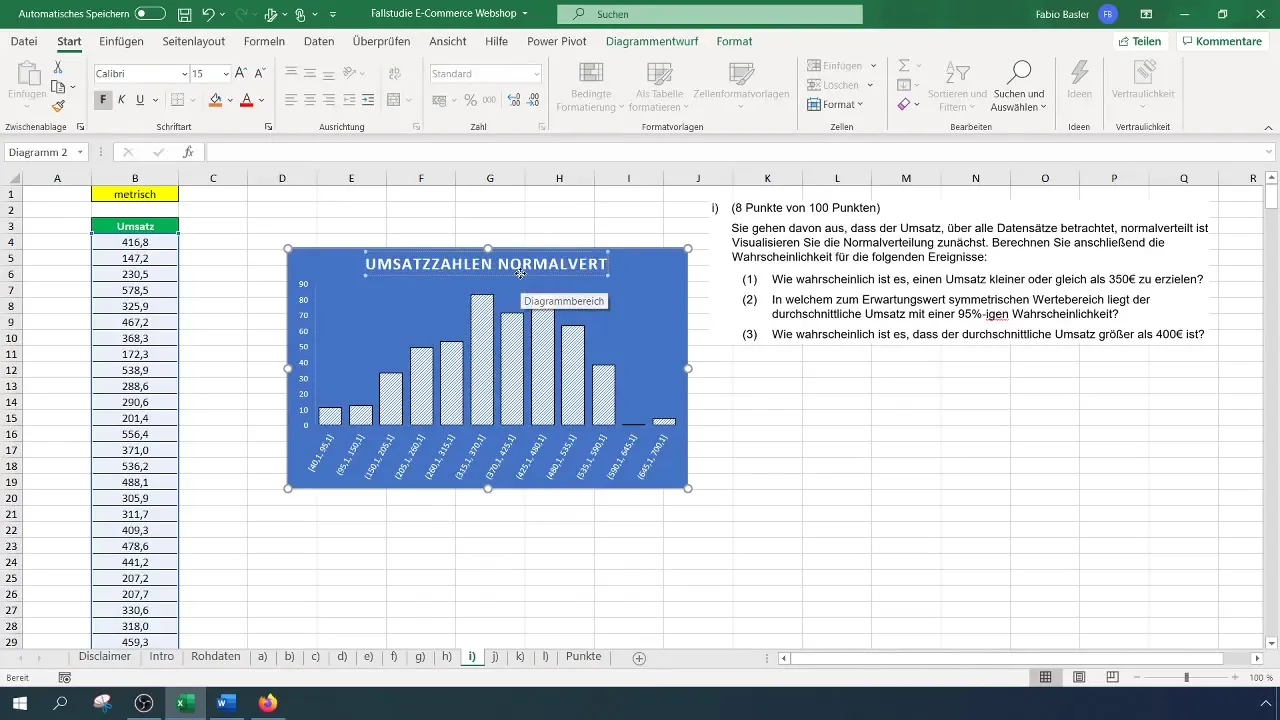
Berekening van waarschijnlijkheden

De volgende taak is om de waarschijnlijkheid te berekenen dat de omzet kleiner of gelijk is aan 350 euro. Hiervoor heb je het gemiddelde en de standaardafwijking van de omzetgegevens nodig.

Om het gemiddelde te berekenen, gebruik je de formule =GEMIDDELDE(A1:A100) (Hier vervangt A1:A100 het daadwerkelijke datumbereik). In jouw voorbeeld zou dit een gemiddelde omzet van 369 euro opleveren.

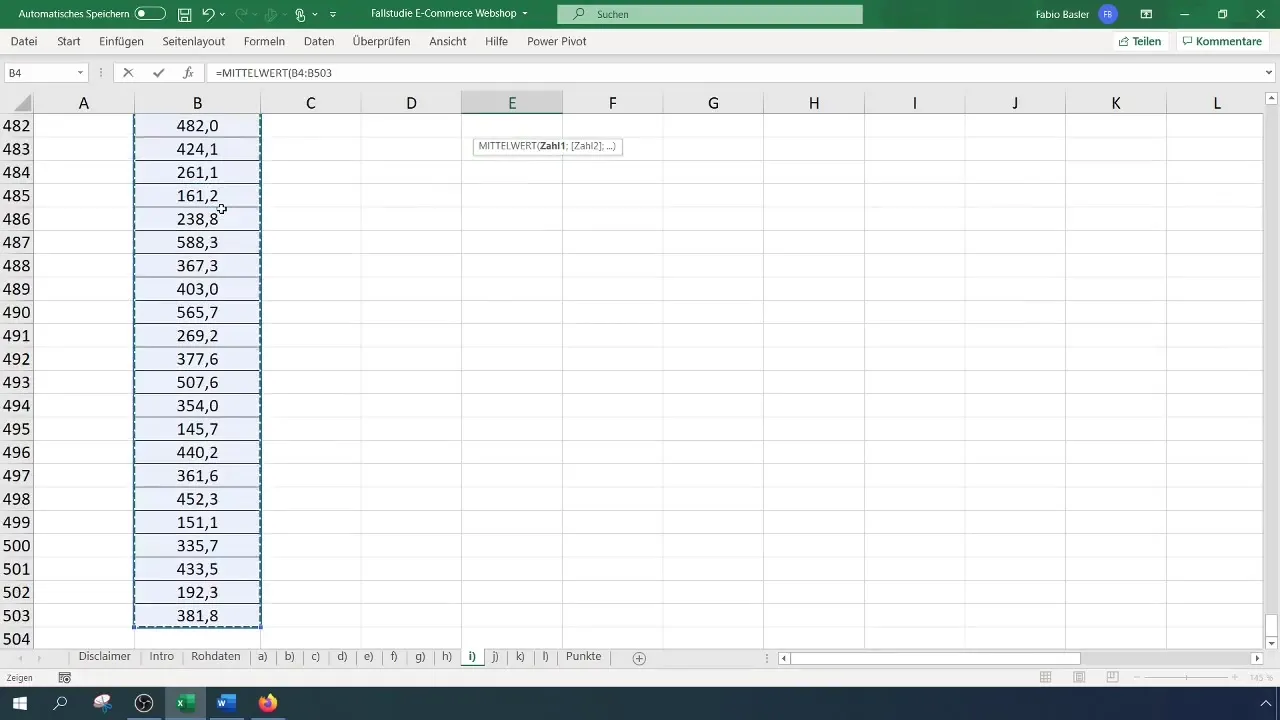
Voor de standaardafwijking gebruik je de formule =STDEV.P(A1:A100), en dit zou in jouw geval ongeveer 124,12 euro opleveren.

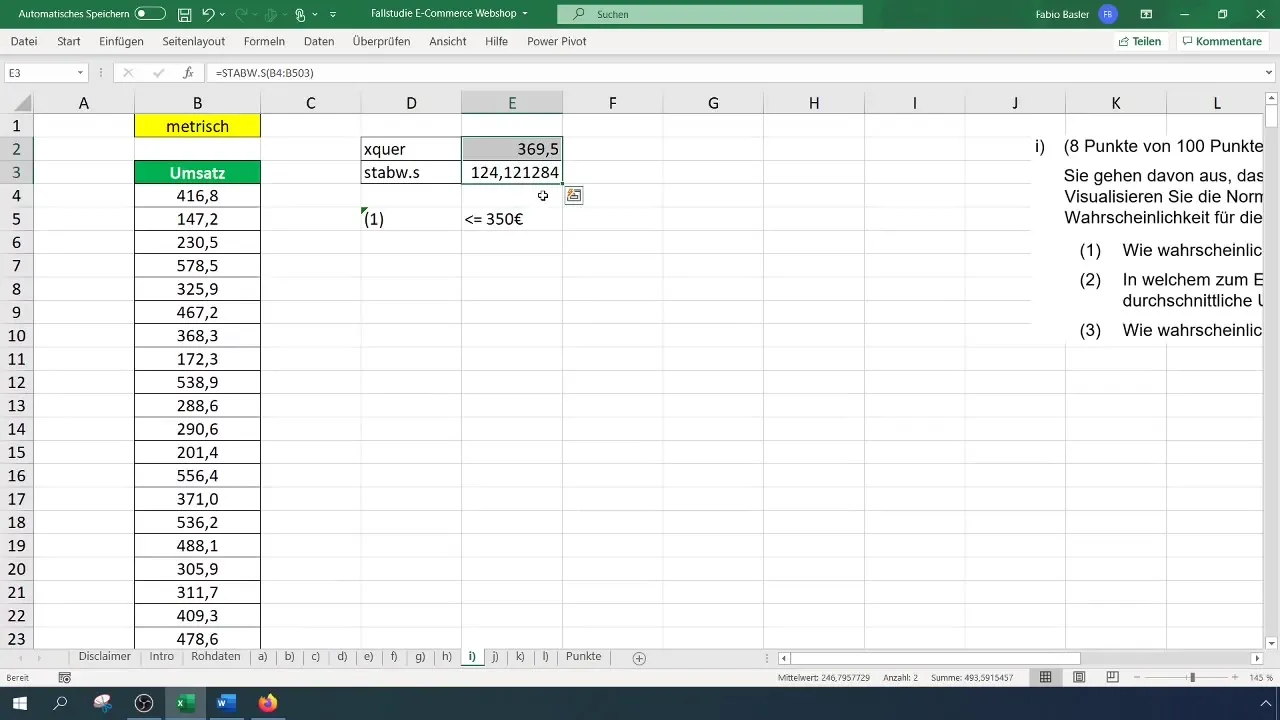
Nu kun je de waarschijnlijkheid voor een omzet van 350 euro berekenen. Dit gebeurt met de formule: =NORM.VERT(350; Gemiddelde; Standaardafwijking; WAAR). Voer de juiste waarden in en druk op Enter.

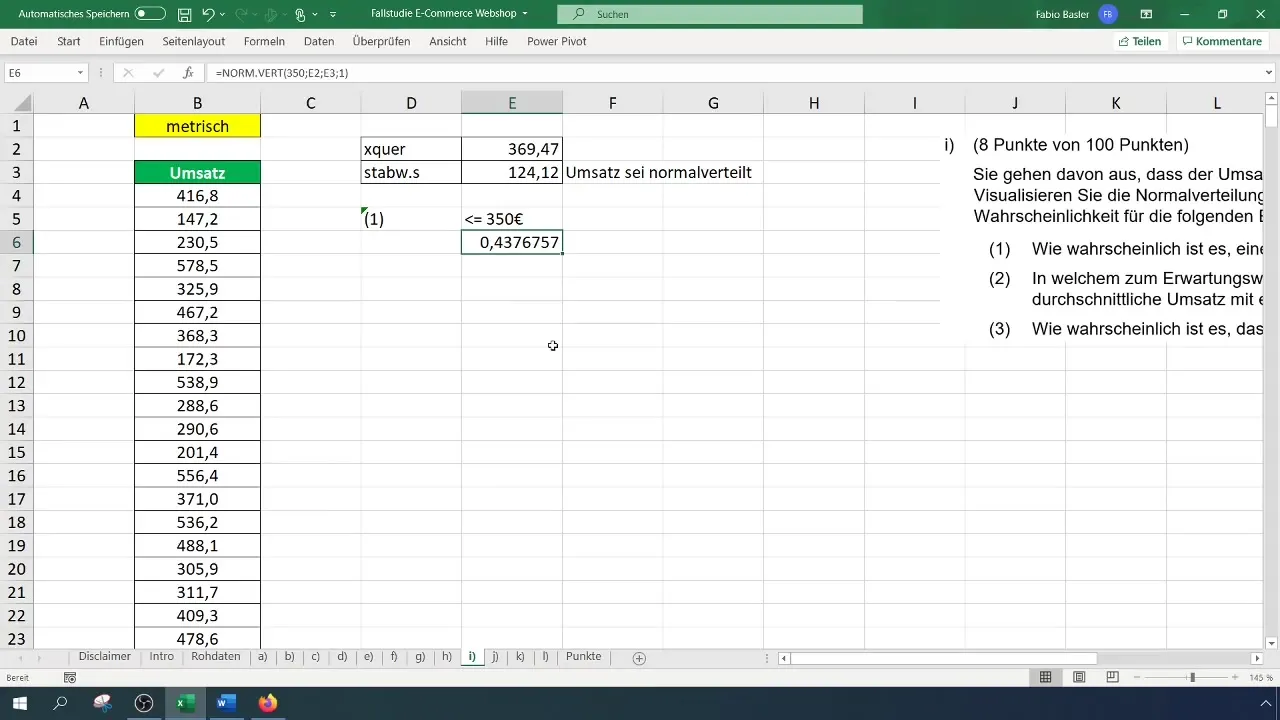
De uitkomst van deze berekening kan aangeven dat de waarschijnlijkheid om een omzet van 350 euro of lager te behalen, ongeveer 43,8% is. Om dit te verduidelijken, kun je de waarden formatteren en de weergave naar procenten wijzigen.

Berekening van het symmetrische waardebereik rond de verwachtingswaarde

De volgende stap is het bepalen van het symmetrische waardebereik rond de verwachtingswaarde met een waarschijnlijkheid van 95%. Hiervoor moet je de kwantitatieve waarde voor 95% bepalen.

Dit doe je door de formule =NORM.INV(0,95) in een cel in te voeren, wat je de kwantielwaarde van 1,65 oplevert.

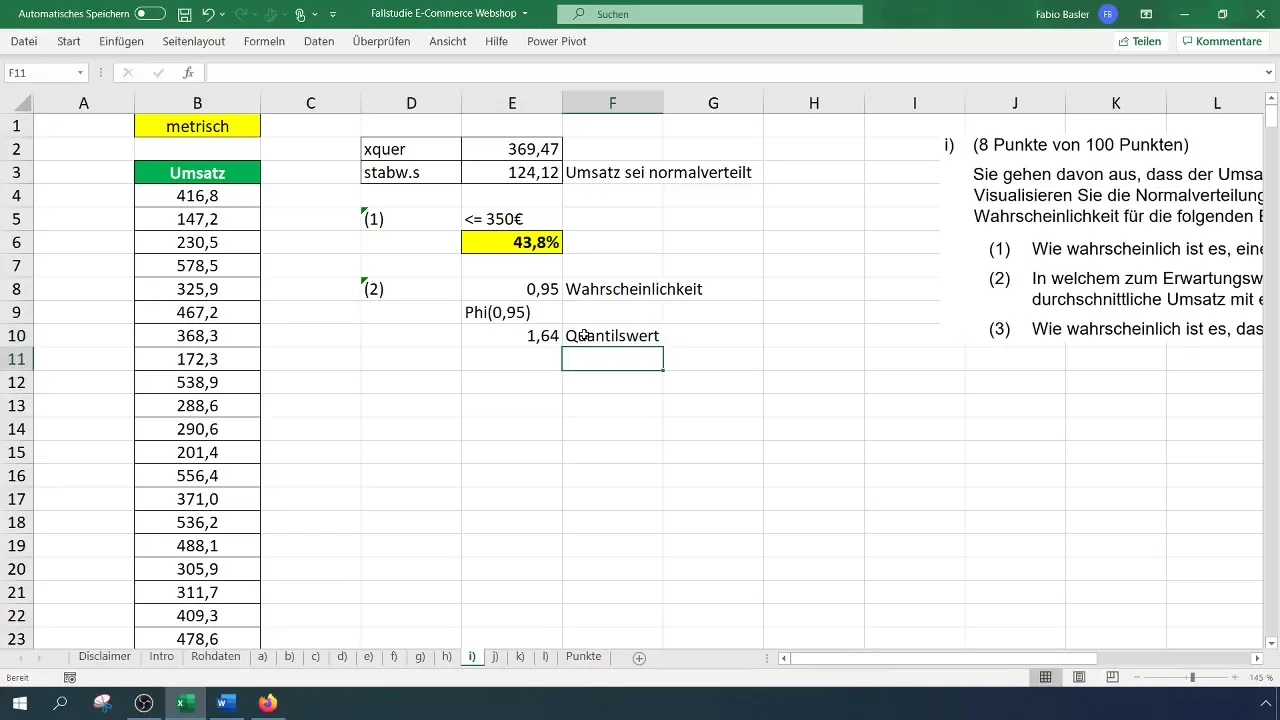
Vervolgens voer je deze berekening in een vergelijking in om het waardebereik te vinden. De formule zou er als volgt uit kunnen zien: Verwachtingswaarde + (Standaardafwijking * Kwantielwaarde). Voer de juiste waarden in en bereken het symmetrische waardebereik.

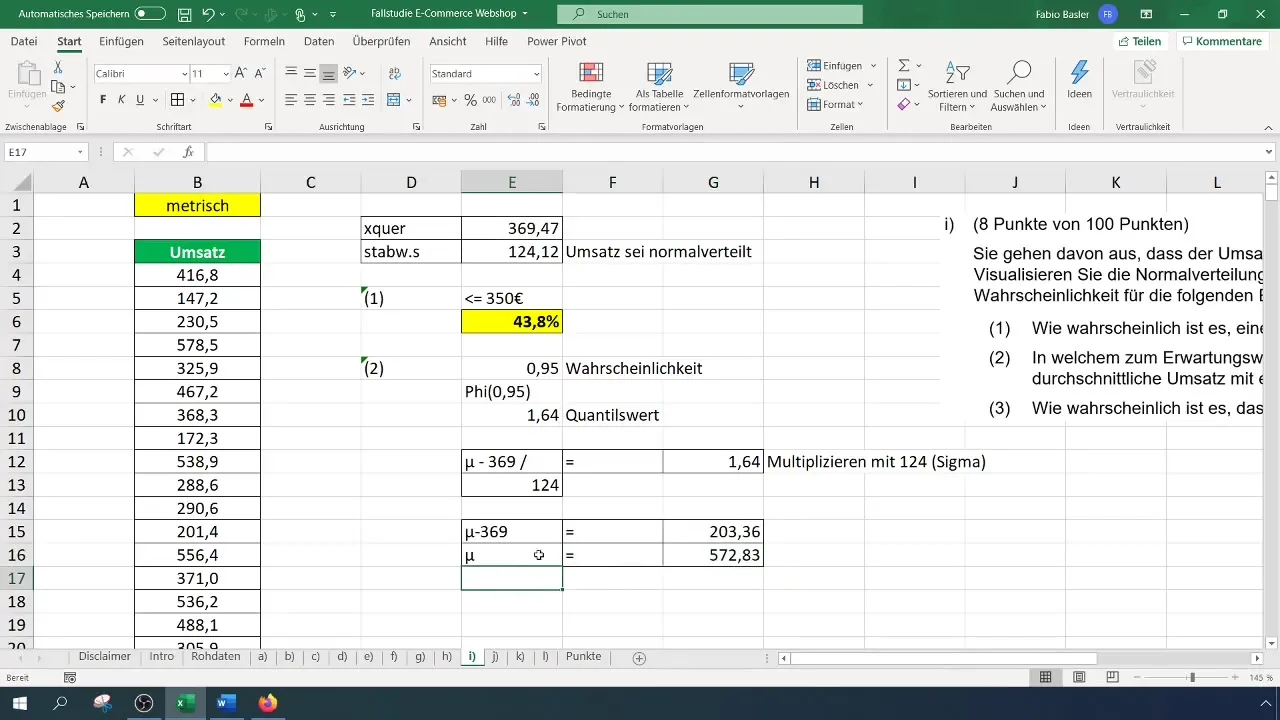
Als je bijvoorbeeld een waarde van 572 euro krijgt, betekent dit dat je met een waarschijnlijkheid van 95% een omzet binnen dit bereik kunt verwachten.

Kansen op hogere omzetten

Voor de laatste berekening zul je de waarschijnlijkheid bepalen dat de omzet groter is dan 400 euro. Hiervoor moet je de formule =1 - NORM.VERD(400; Gemiddelde; Standaardafwijking; WAAR) gebruiken.

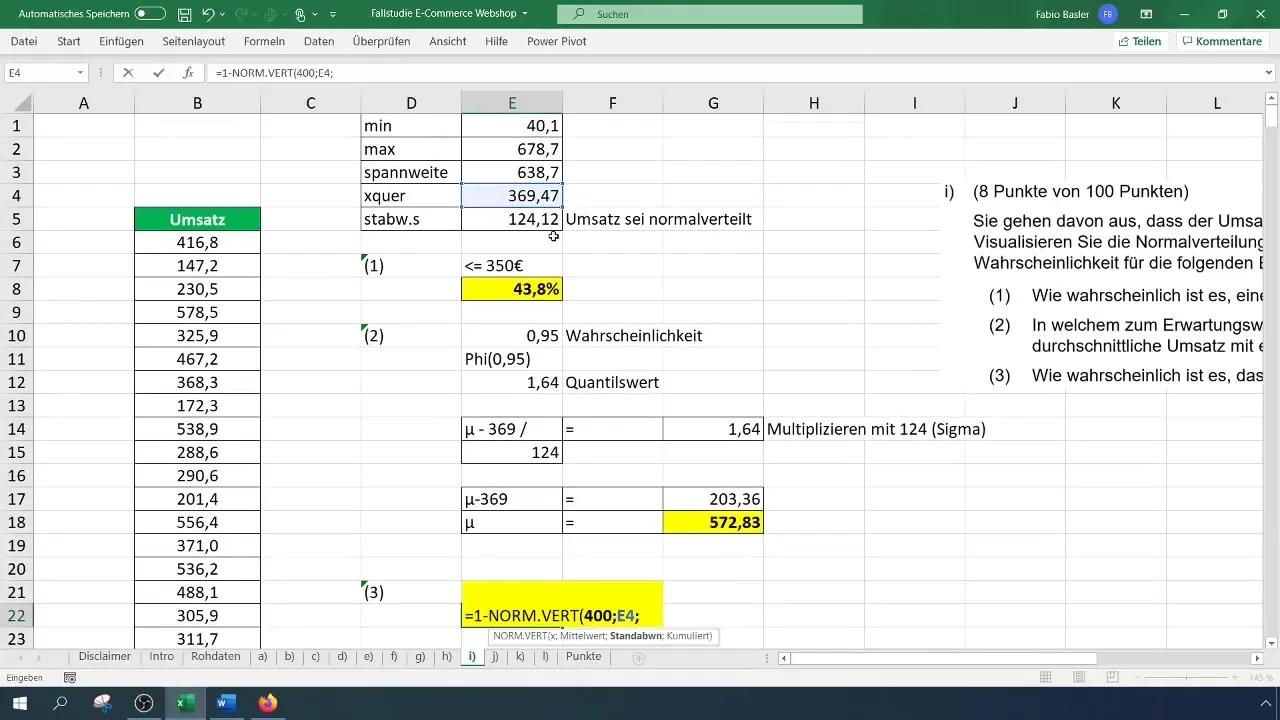
De waarschijnlijkheid kan hier ook rond 40% liggen. Deze waarden zijn zinvol om te evalueren. Als je naar de schaal in het histogram kijkt, kun je de consistentie van het percentage van de hogere omzetten begrijpen.

Samenvatting

In deze handleiding heb je geleerd hoe je met Excel de normale verdeling kunt gebruiken om waarschijnlijkheden te berekenen. Gebaseerd op praktische voorbeelden uit een enquête, heb je geleerd hoe je zowel grafisch als rekenkundig met gegevens kunt werken. Het begrip van deze concepten zal je helpen om statistische analyses succesvol uit te voeren in je projecten.