Bereken het betrouwbaarheidsinterval voor de omzet in Excel

Het berekenen van betrouwbaarheidsintervallen is een essentieel onderdeel van de statistische analyse, vooral wanneer het gaat om het trekken van conclusies over een populatie op basis van een steekproef. In deze handleiding laat ik je zien hoe je in Excel een tweezijdig betrouwbaarheidsinterval kunt berekenen voor de gemiddelde omzet van een enquête. Je zult leren welke verschillende stappen nodig zijn om van ruwe gegevens naar het uiteindelijke betrouwbaarheidsinterval te gaan en hoe je deze methodiek in Excel implementeert.

Belangrijkste inzichten

• Een tweezijdig betrouwbaarheidsinterval geeft aan binnen welke grenzen de werkelijke gemiddelde omzet met een bepaalde mate van betrouwbaarheid kan liggen.
• Voor de berekening heb je het gemiddelde, de standaardafwijking, de steekproefgrootte en het overeenkomstige t-kwantiel nodig.
• Excel biedt de benodigde functies om deze waarden te berekenen en het betrouwbaarheidsinterval visueel weer te geven.

Stapsgewijze handleiding

Stap 1: Voorbereiden van gegevens

Zorg er eerst voor dat je de relevante gegevens in Excel beschikbaar hebt. Voor het voorbeeld bekijken we alleen de normale klanten, omdat de gemiddelde omzet alleen voor deze groep berekend moet worden.

Je kunt de gegevens op je werkblad markeren en kopiëren om ze in een nieuw gebied in te voegen. Dit helpt bij het filteren van je analyse voor de relevante klantengroepen.

Stap 2: Verzamelen basisinformatie

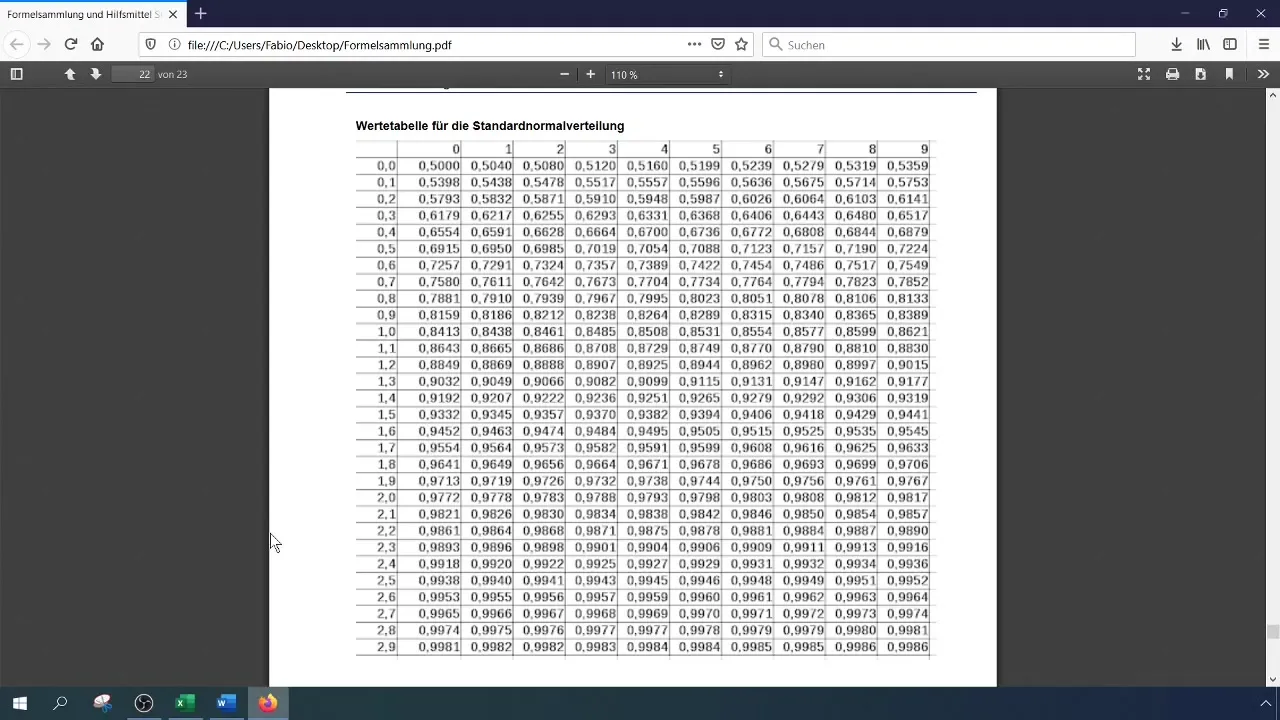
Maak een eenvoudige tabel in Excel waarin je alle belangrijke parameters vastlegt. Dit zijn de steekproefgrootte (n), het gemiddelde (x̄), de standaardafwijking (σ) en het relevante kwantiel. We weten al dat we een normale verdeling aannemen en geen variantie beschikbaar hebben.

Stap 3: Berekenen steekproefgrootte (n)

Om het aantal waarnemingen voor de normale klanten te bepalen, moet je de relevante gegevens knippen en het aantal vinden met de FORMULE =AANTAL(). In dit geval zou je 336 waarnemingen moeten krijgen van de gefilterde gegevens.

Stap 4: Bereken gemiddelde (x̄)

Bereken het gemiddelde van de omzet door de formule =GEMIDDELDE() toe te passen. Dit geeft je de gemiddelde omzet voor de normale klanten, die in ons voorbeeld 362,80 euro bedraagt.

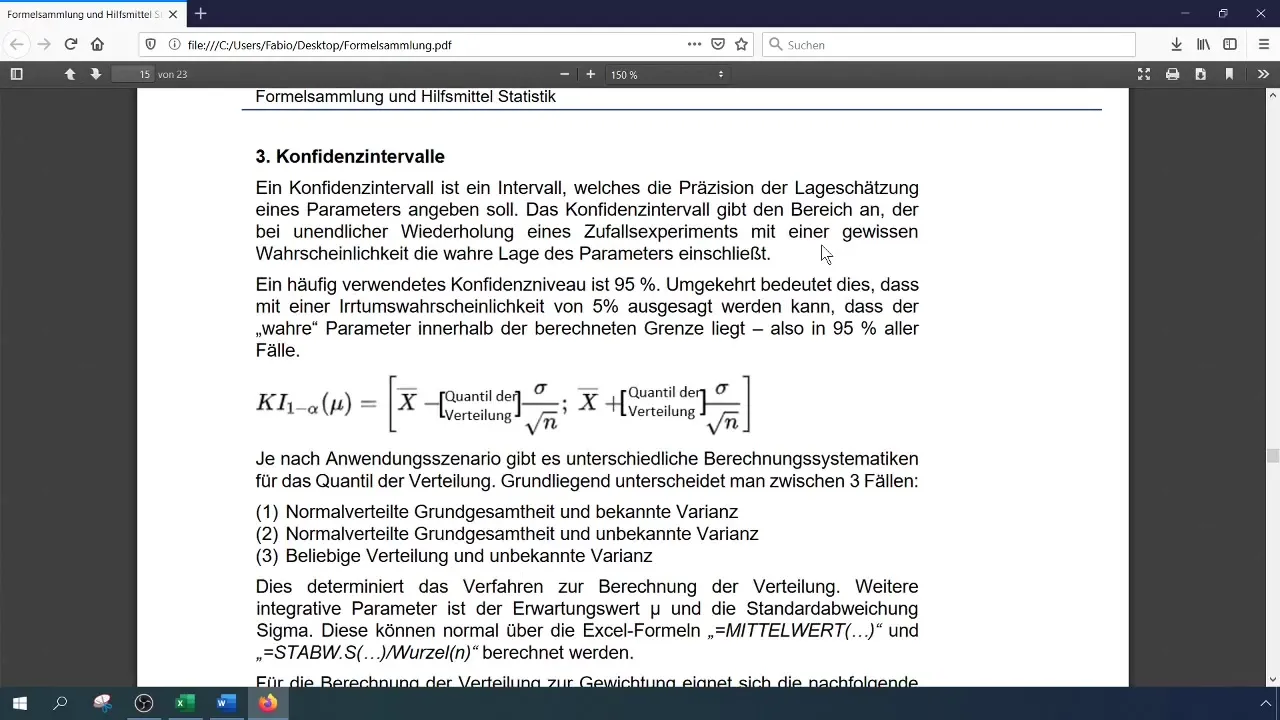
Stap 5: Bepaal standaardafwijking (σ)

Gebruik de formule =STDEV.S() om de standaardafwijking te berekenen. Deze is nodig voor inductieve statistiek, daarom gebruiken we de standaardafwijking voor de steekproef. De berekende waarde is 123 euro.

Stap 6: Sigma (σ / √n) berekenen

Bereken nu de standaardafwijking voor het gemiddelde door de standaardafwijking te delen door de vierkantswortel van de steekproefgrootte. Gebruik de formule: =standaardafwijking/WORTEL(steekproefgrootte).

Stap 7: t-kwantiel vinden

Gezien het feit dat we een normale verdeling hebben met een onbekende variantie, moeten we het t-kwantiel bepalen. Gebruik de Excel-functie =T.INV.2T() met opgave van het alfaniveau (0,08) en de vrijheidsgraden (n-1). In jouw geval levert dit een t-waarde van 1,8 op.

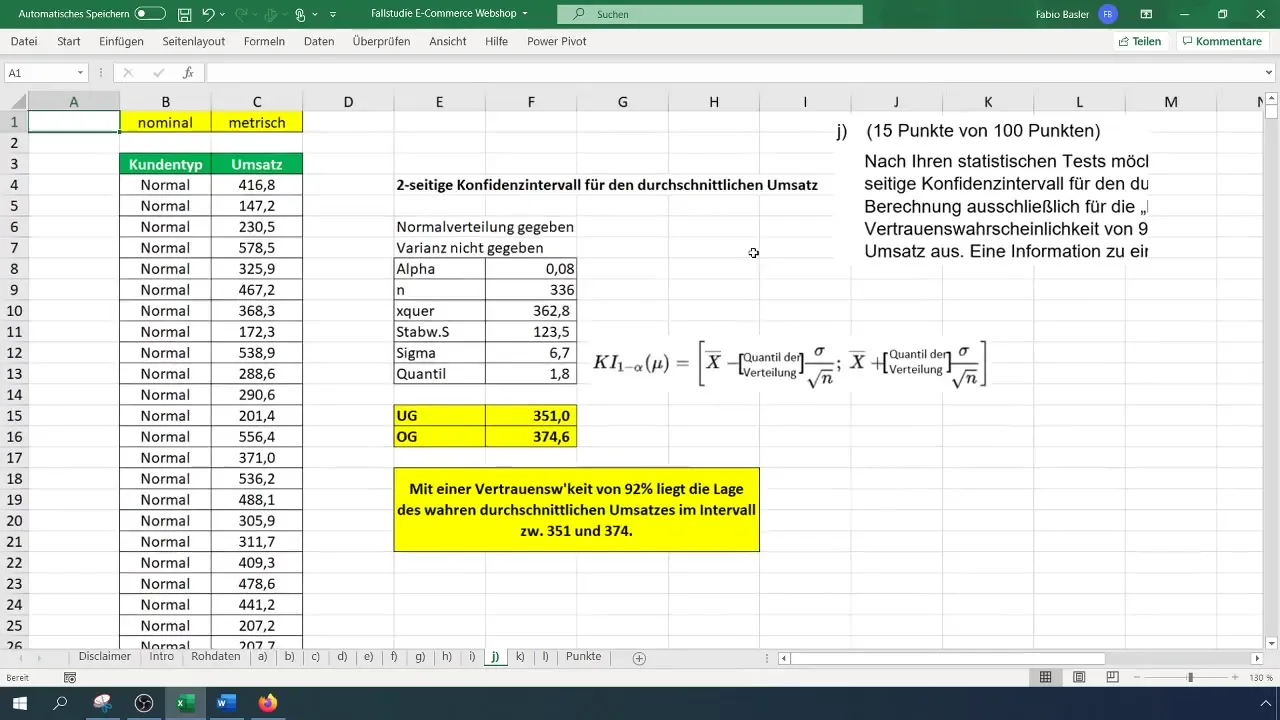
Stap 8: Ondergrens van betrouwbaarheidsinterval berekenen

Bereken nu de ondergrens van het betrouwbaarheidsinterval. De formule is: =Gemiddelde - (t-waarde * Sigma). Dit geeft je de ondergrens, die in ons voorbeeld 351 euro bedraagt.

Stap 9: Bovengrens van het betrouwbaarheidsinterval berekenen

Nu kun je de bovengrens van het betrouwbaarheidsinterval berekenen. De formule is vergelijkbaar, alleen voeg je deze keer de t-waarde toe aan je gemiddelde: =Gemiddelde + (t-waarde * Sigma). De bovengrens bedraagt dus 374 euro.

Stap 10: Representatie van het betrouwbaarheidsinterval

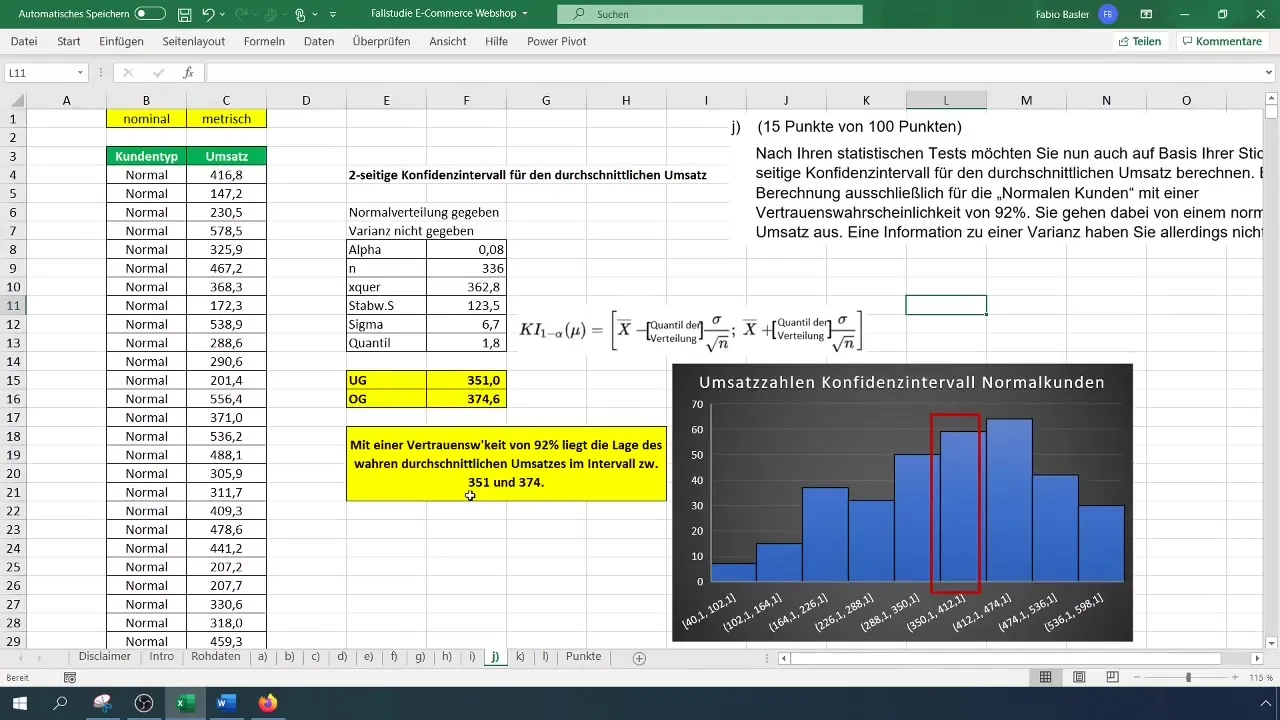
Om je resultaten te visualiseren, kun je in Excel een histogram maken en het betrouwbaarheidsinterval markeren. Trek een lijn tussen de onder- en bovengrens om aan te geven in welk gebied de werkelijke gemiddelde omzet van normale klanten met een betrouwbaarheid van 92% ligt.

Stap 11: Interpretatie en conclusie

Je kunt nu concluderen dat met een betrouwbaarheidsniveau van 92% het werkelijke gemiddelde omzet van normale klanten tussen 351 en 374 euro ligt. Dit is belangrijk voor verdere beslissingen in jouw bedrijf.

Samenvatting

In deze handleiding heb je geleerd hoe je een tweezijdig betrouwbaarheidsinterval voor de gemiddelde omzet in Excel kunt berekenen. Je hebt alle benodigde stappen doorlopen, van het voorbereiden van de gegevens tot de grafische weergave en interpretatie van de resultaten.