Statistische berekeningen zijn een onmisbaar onderdeel van gegevensanalyse, vooral in een E-commerce omgeving. De historische gegevensanalyse maakt het mogelijk om waarschijnlijkheden te bepalen die cruciaal zijn voor bedrijven. In deze handleiding leer je hoe je waarschijnlijkheden kunt berekenen met behulp van de Poisson-verdeling in Excel, gebaseerd op een casestudy van een enquête.
Belangrijkste bevindingen De Poisson-verdeling stelt je in staat om de waarschijnlijkheid van gebeurtenissen te bepalen die zich voordoen binnen een vaste tijdsperiode. In dit voorbeeld bereken je de waarschijnlijkheid dat meer dan twee, maar hoogstens vier klanten binnen een uur iets kopen in een E-commerce winkel, evenals de waarschijnlijkheid dat meer dan twee klanten in totaal iets kopen.
Stap-voor-stap handleiding
Laten we beginnen met het berekenen van de waarschijnlijkheden voor de beschreven gebeurtenissen.
Stap 1: Begrijp de basisprincipes van de Poisson-verdeling
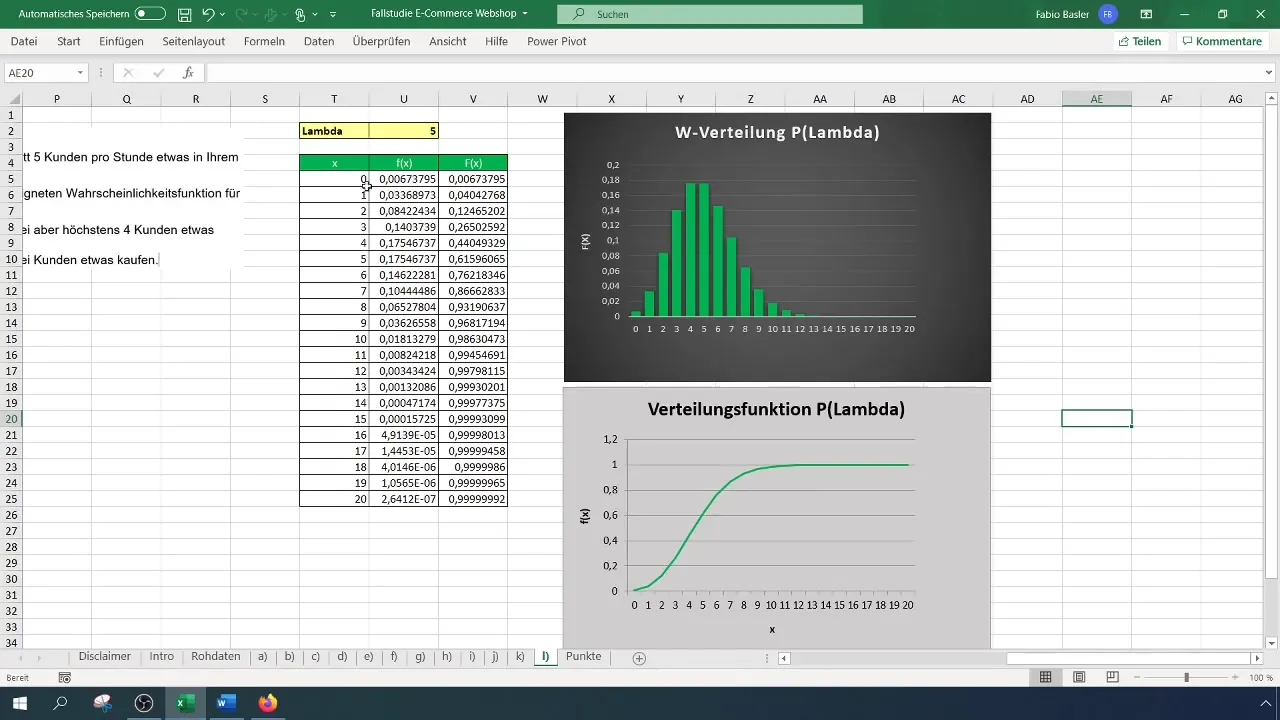
Het is allereerst belangrijk dat je begrijpt wat de Poisson-verdeling is. Deze discrete kansverdeling wordt gebruikt om het aantal gebeurtenissen in vaste tijdsperioden te kwantificeren. In het huidige voorbeeld hebben we een gemiddelde van vijf aankopen per uur. Dit zet je om in een Lambda-waarde (λ = 5).

Stap 2: Bereid de gegevens voor in Excel
Open Excel en maak een nieuw werkblad. Zorg ervoor dat je de relevante parameters (Lambda en het aantal gewenste gebeurtenissen) goed zichtbaar hebt.
Stap 3: Bepaal waarschijnlijkheden voor klantaankopen
Voor het eerste scenario wil je berekenen wat de waarschijnlijkheid is dat meer dan twee en hoogstens vier klanten iets kopen. Hiervoor moet je eerst de waarschijnlijkheden voor twee en vier klanten berekenen en vervolgens hun verschil bepalen.

Stap 4: Gebruik de Excel-formule voor de Poisson-verdeling
Gebruik de functie POISSON.WAARSCHIJNLIJKHEID om de waarschijnlijkheden te berekenen. De formule is als volgt:
- Voor twee kopers: =POISSON.WAARSCHIJNLIJKHEID(2; 5; WAAR).
- Voor vier kopers: =POISSON.WAARSCHIJNLIJKHEID(4; 5; WAAR).
Stap 5: Resultaten interpreteren
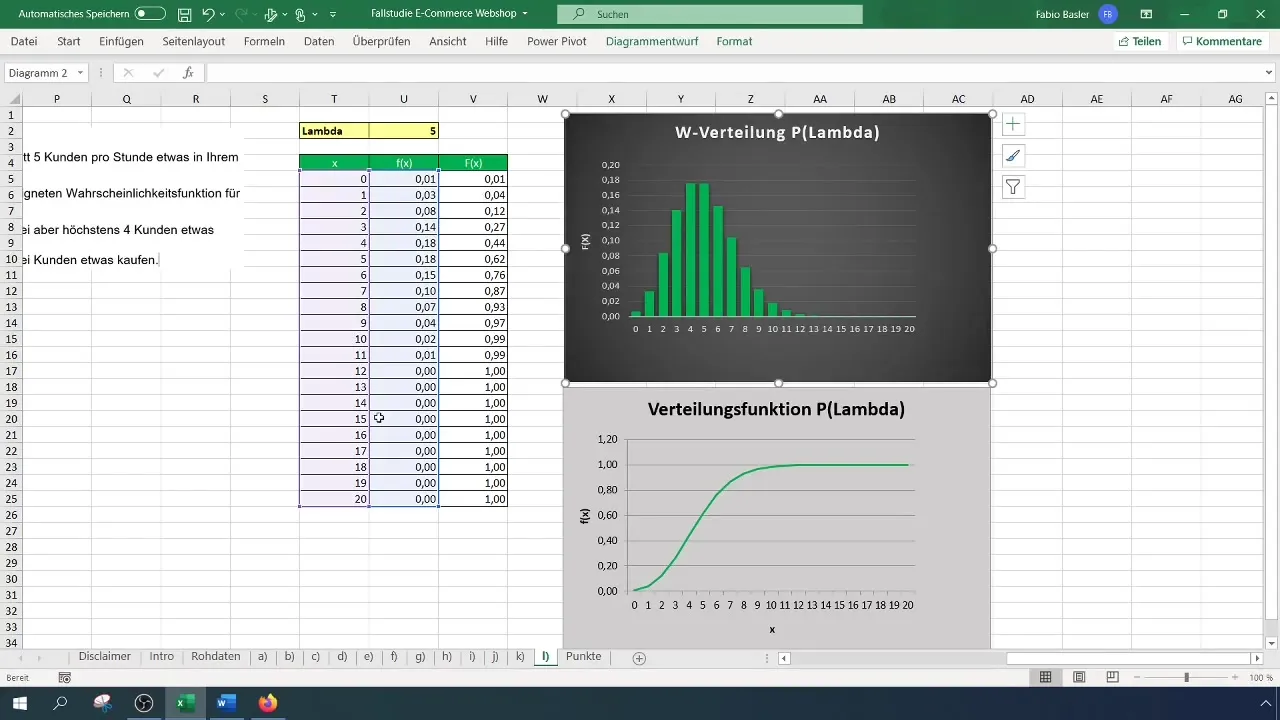
Na het toepassen van de formules krijg je twee waarschijnlijkheden, bijvoorbeeld 12% voor twee klanten en 44% voor vier klanten. Trek nu de waarschijnlijkheid voor twee kopers af van die voor vier kopers, wat je een waarschijnlijkheid van 32% geeft dat meer dan twee, maar hoogstens vier klanten iets kopen.
Stap 6: Bereken meer waarschijnlijkheden
Op dit moment gaat het erom de waarschijnlijkheid te berekenen dat meer dan twee klanten iets kopen in jouw E-commerce shop. Hiervoor bereken je eerst de waarschijnlijkheid voor precies twee kopers en trek je dit resultaat af van 1.
Stap 7: Gebruik de Excel-formule voor meer dan twee kopers
De Excel-formule is als volgt: =1 - POISSON.WAARSCHIJNLIJKHEID(2; 5; WAAR). Dit geeft je de waarschijnlijkheid dat meer dan twee klanten iets kopen, die in dit geval 88% bedraagt.
Stap 8: Samenvatting van de resultaten
Nadat je alle berekeningen hebt uitgevoerd, noteer je de belangrijkste waarschijnlijkheden. Je hebt ontdekt dat de waarschijnlijkheid dat meer dan twee, maar hoogstens vier klanten bestellen 32% bedraagt, terwijl de waarschijnlijkheid dat meer dan twee klanten in totaal iets kopen 88% bedraagt.
Samenvatting
In deze handleiding heb je geleerd hoe je de Poisson-verdeling kunt gebruiken om waarschijnlijkheden in Excel te berekenen. Je hebt stappen uitgevoerd om waarschijnlijkheden voor specifieke gebeurtenissen te berekenen en interpreteren.
Veelgestelde vragen
Wat is de Poisson-verdeling?De Poisson-verdeling is een discrete kansverdeling die aangeeft hoe vaak een gebeurtenis plaatsvindt binnen een vaste tijdsperiode.
Hoe bereken ik waarschijnlijkheden met de Poisson-verdeling in Excel?Je gebruikt de functie POISSON.WAARSCHIJNLIJKHEID om waarschijnlijkheden voor verschillende waarden te berekenen.
Wat betekent een Lambda-waarde van 5?Een Lambda-waarde van 5 betekent dat gemiddeld vijf gebeurtenissen (bijv. aankopen) optreden in de gedefinieerde tijdsperiode (bijv. een uur).
Welke waarden moet ik opgeven voor de Poisson-verdeling?Je moet het aantal gewenste gebeurtenissen (x), het gemiddelde (λ) en aangeven of je cumulatieve waarschijnlijkheden wilt berekenen.
Waarom is de Poisson-verdeling belangrijk voor E-commerce?De Poisson-verdeling helpt bij het analyseren van kooppatronen en het voorspellen van de waarschijnlijkheid van klantactiviteiten, wat cruciale beslissingen in marketing en voorraadbeheer kan ondersteunen.


