Korrelasjonsanalyse og Pearson-koeffisient i Excel

Analysen av sammenhenger er en grunnleggende ferdighet som er uunnværlig i mange vitenskapelige og forretningsmessige områder. Ved hjelp av Excel kan du beregne Pearsons korrelasjonskoeffisient for å kvantitativt måle relasjoner mellom variabler. I denne veiledningen viser jeg deg trinn for trinn hvordan du kan utføre en korrelasjonsanalyse for omsetningen av smarttelefoner og bærbare datamaskiner i Excel. Denne prosessen illustrerer ikke bare bruken av statistiske konsepter, men også den enkle håndteringen av Excel for dataanalyse.

Viktigste funn

• Pearson-korrelasjonskoeffisienten gir en kvantitativ vurdering av forholdet mellom to variabler.
• Kjenn de ulike metodene for å beregne korrelasjonskoeffisienten i Excel.
• Visualisering av resultater gjennom diagrammer letter forståelsen av forholdene mellom variabler.

Trinn-for-trinn-guide

Den følgende fremgangsmåten viser deg hvordan du kan beregne Pearsons korrelasjonskoeffisient i Excel. Vi fokuserer på omsetningen av smarttelefoner og bærbare datamaskiner for å vise en klar og praktisk anvendelse.

For å starte korrelasjonsanalysen, åpne først en ny Excel-arbeidsbok eller bruk en eksisterende der de relevante dataene allerede finnes.

Først må du forsikre deg om at de relevante omsetningene for smarttelefoner og bærbare datamaskiner er inntastet i to separate kolonner. Disse kolonnene danner datagrunnlaget som analysen bygger på. Sørg for at dataene er fullstendige og korrekte for å unngå feilaktige resultater.

Etter at dataene er inntastet, merk de to kolonnene med omsetningene. For å beregne korrelasjonskoeffisienten, skriv inn formelen =KORREL() i en tom celle, etterfulgt av de to datoområdene. Denne funksjonen beregner Pearsons korrelasjonskoeffisient basert på de valgte dataene.

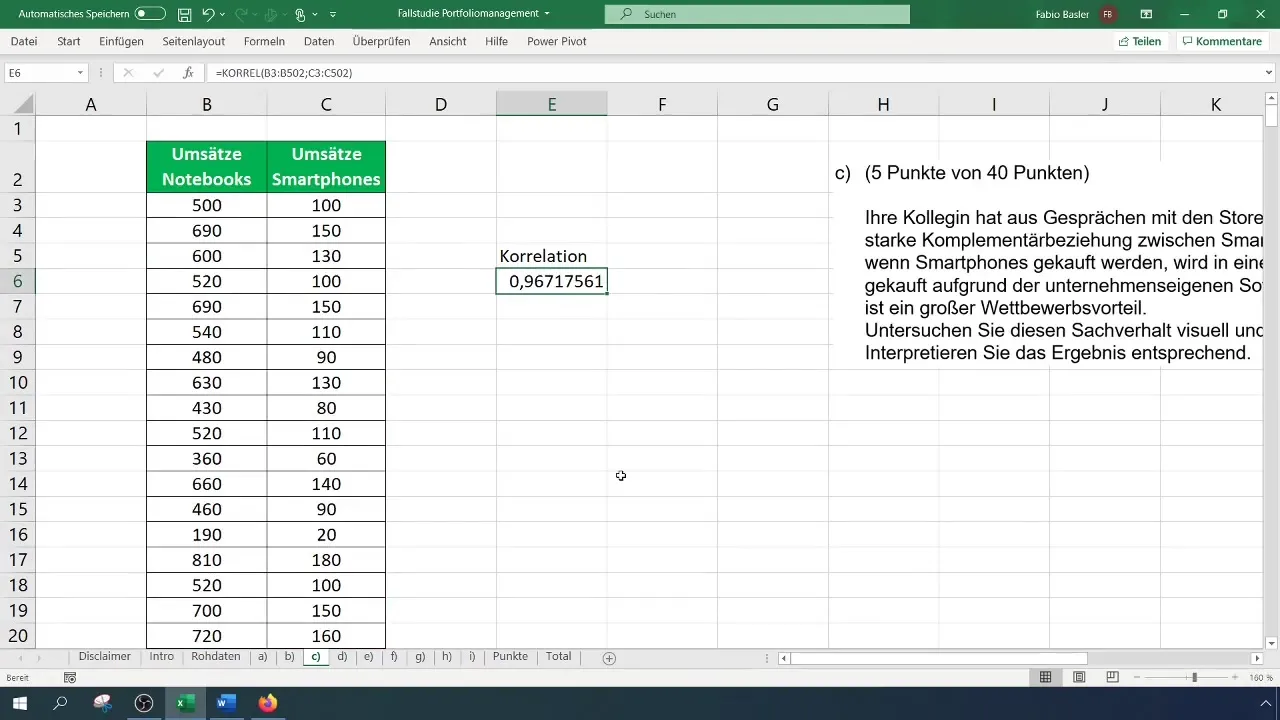
Ved å bruke formelen =KORREL(Område1; Område2), velg hele området av kolonnen som representerer bærbare datamaskiners omsetning, etterfulgt av området med smarttelefonenes omsetning. Resultatet vil vise korrelasjonsverdien mellom disse variablene. En høy korrelasjon, for eksempel 0,96, indikerer en sterk positiv relasjon.

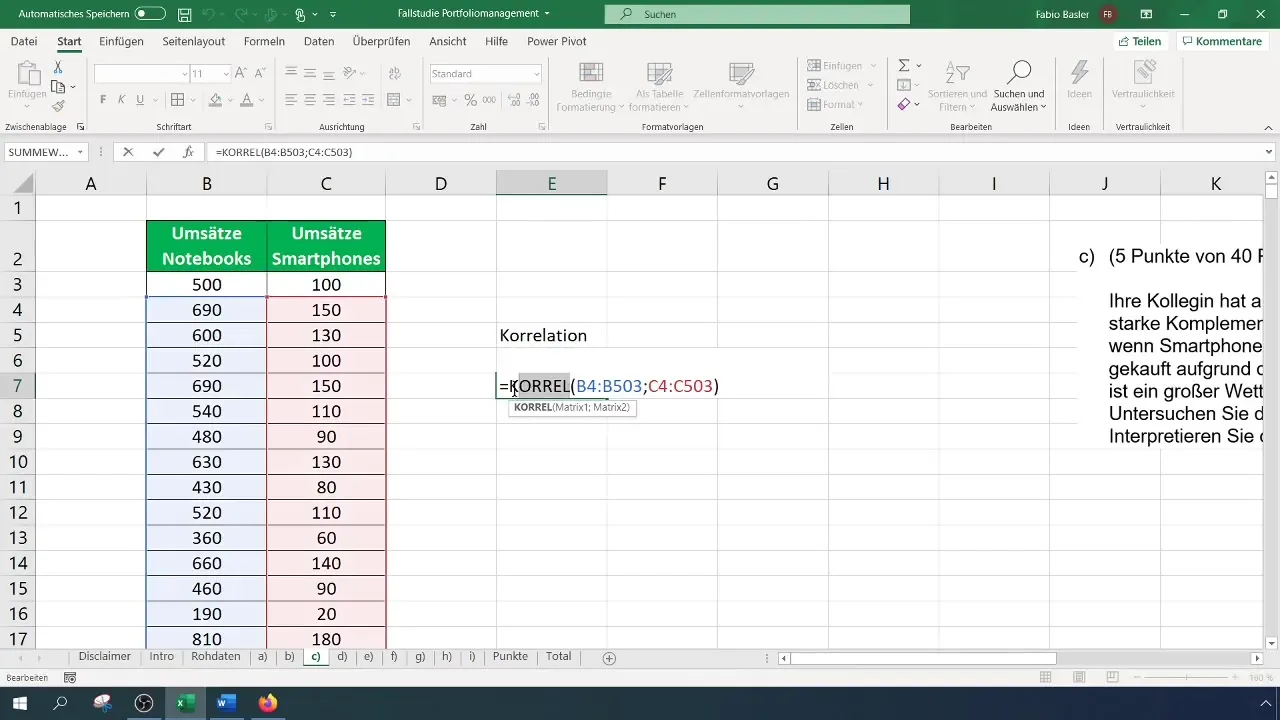
I tillegg til KORREL-funksjonen kan du også bruke funksjonen =PEARSON(), som gir samme resultat. Angi denne funksjonen på samme måte som tidligere og velg datoområdene for å beregne korrelasjonen.

En annen interessant måte å gjennomføre en korrelasjonsanalyse på er gjennom dataanalysefunksjonen i Excel. For å aktivere denne funksjonen, gå til menyen "Fil" og deretter til "Alternativer". Under Add-Ins kan du aktivere Dataanalyse-alternativet hvis det ikke allerede er aktivert.

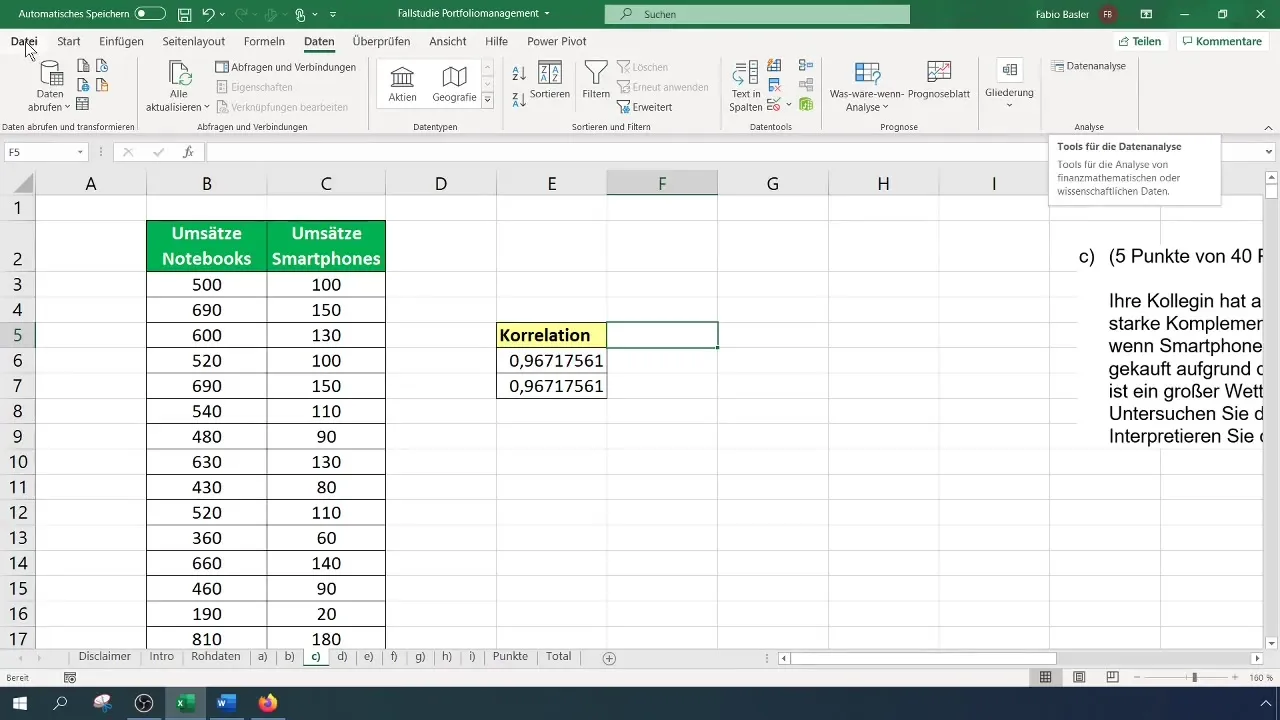
Etter å ha aktivert dataanalysefunksjonen, velger du "Dataanalyse" fra menylinjen og klikker på "Korrelasjon". En inndata-maske åpner seg hvor du definerer inndataområdet for dataene, inkludert kolonneoverskriftene.

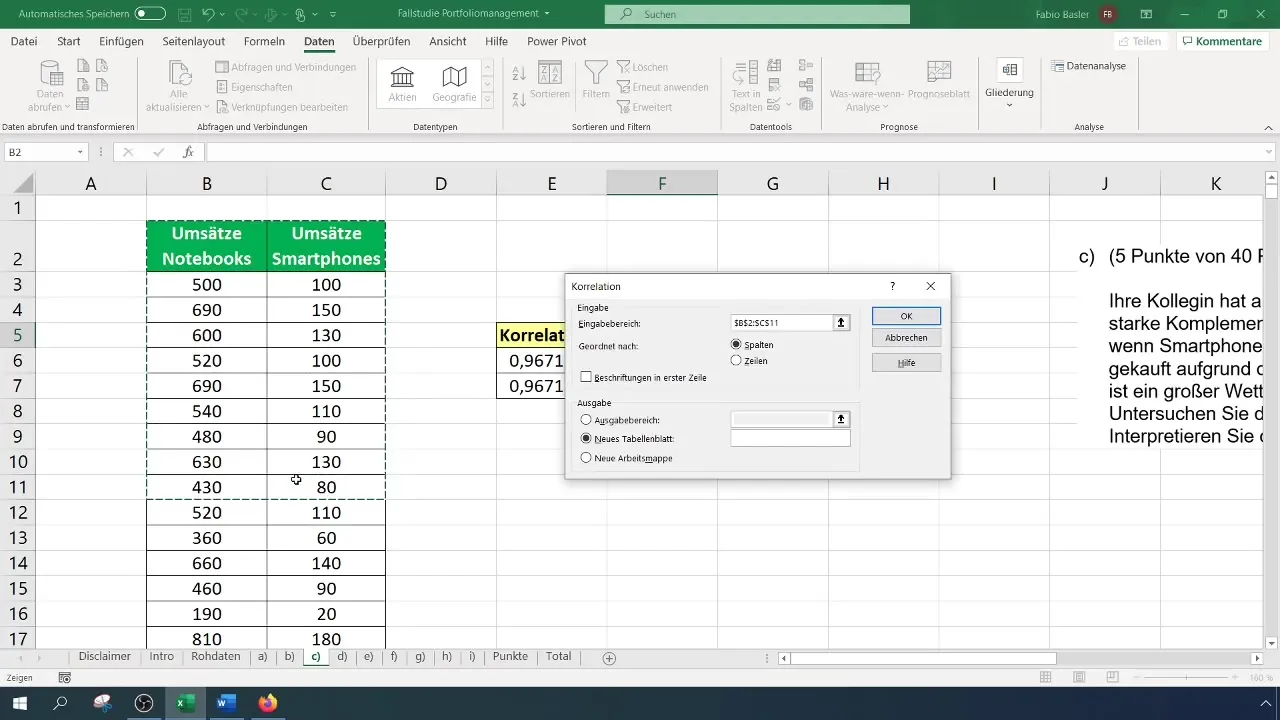
Ved å angi utdataområdet, velger du en tom celle der resultatene vil vises. Ved å bekrefte inndataene genereres en korrelasjonsmatrise som viser alle relasjoner innad i de angitte dataene. Her vil du igjen kunne observere den høye korrelasjonen på omtrent 0,96.

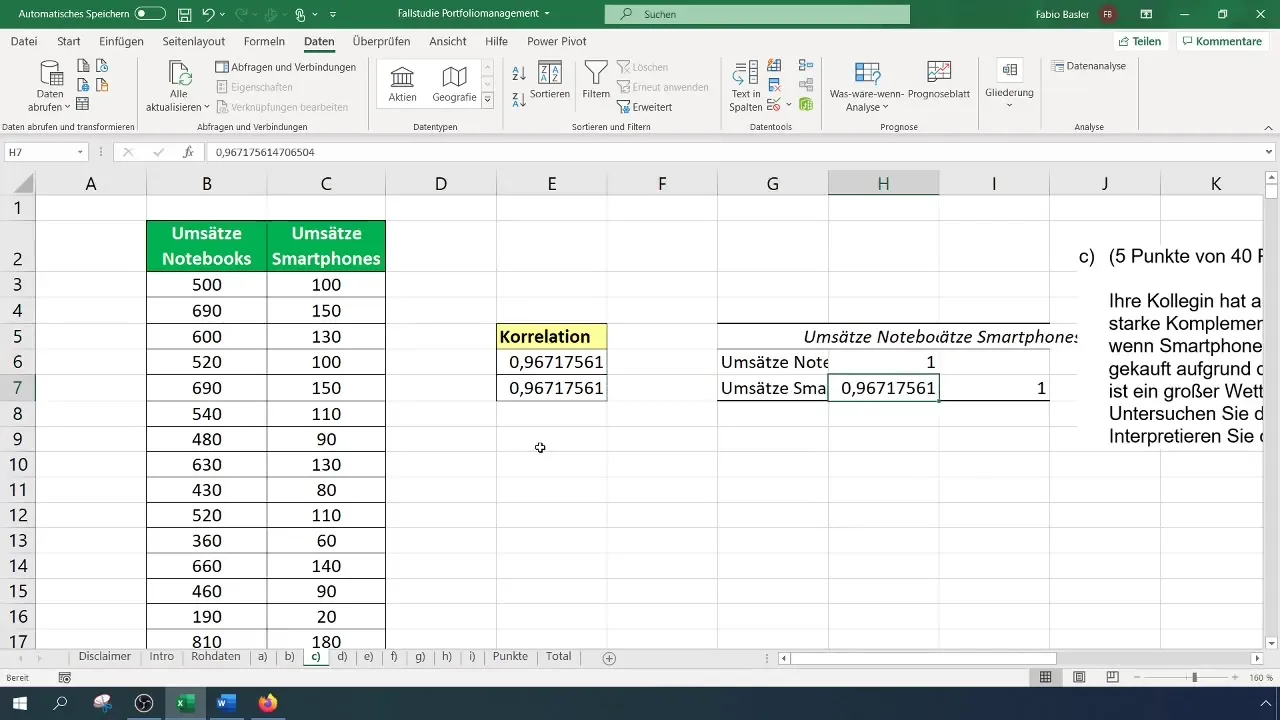
For å visuelt fremstille relasjonen mellom variablene, egner seg et punktdiagram. Velg en tom celle og sett inn et XY-diagram. Høyreklikk på diagrammet og velg "Velg data".

Legg til omsetning for både smarttelefoner og bærbare datamaskiner. Denne visuelle fremstillingen viser deg hvordan punktene mellom de to variablene er fordelt og tydeliggjør forholdet gjennom klynger-effekter.

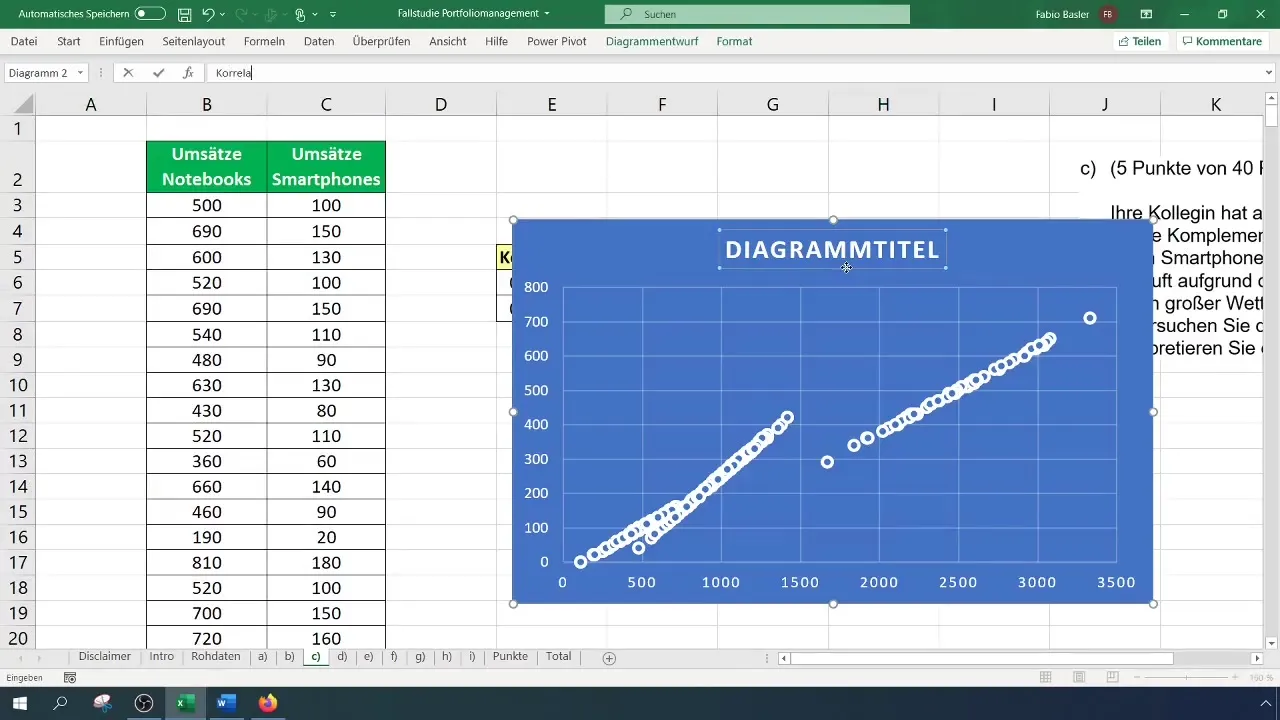
En ekstra analyse til relasjoner er å legge til en trendlinje i diagrammet. Klikk på plusstegnet øverst til høyre i diagrammet og aktiver trendlinjealternativet. Du kan også vise formelen og determinasjonskoeffisienten R² for videre analyse.

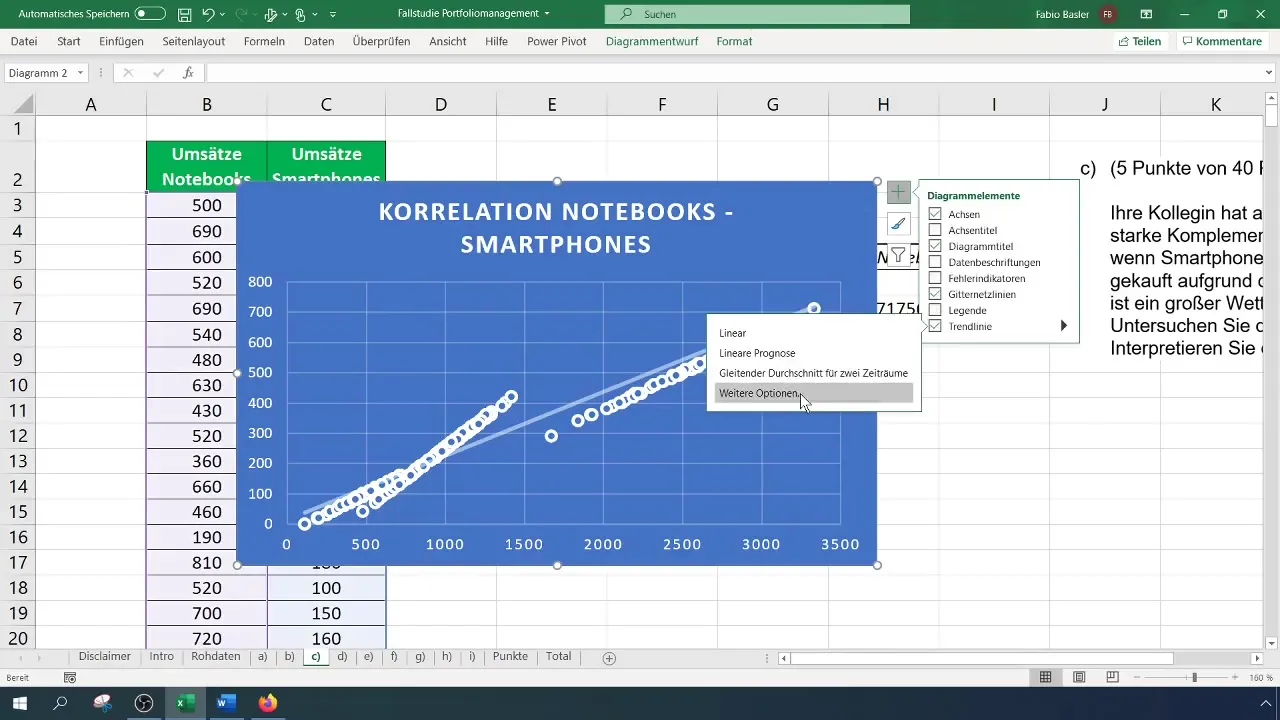
Bestemthetsmålet angir hvor godt trendlinjen beskriver dataene og er den kvadratiske verdien av korrelasjonskoeffisienten. En R² på omtrent 0,935 styrker styrken av forholdet mellom bærbare datamaskiner og smarttelefoner, noe som støtter den tidligere beregnede korrelasjonen.

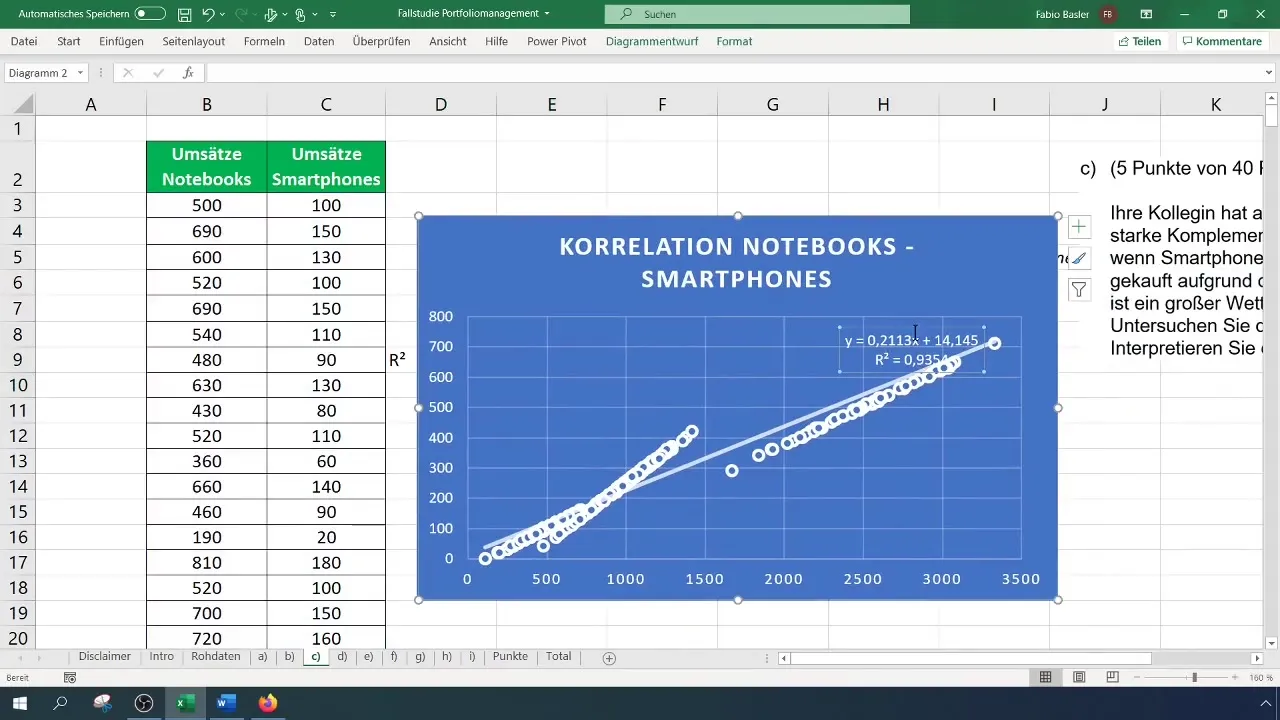
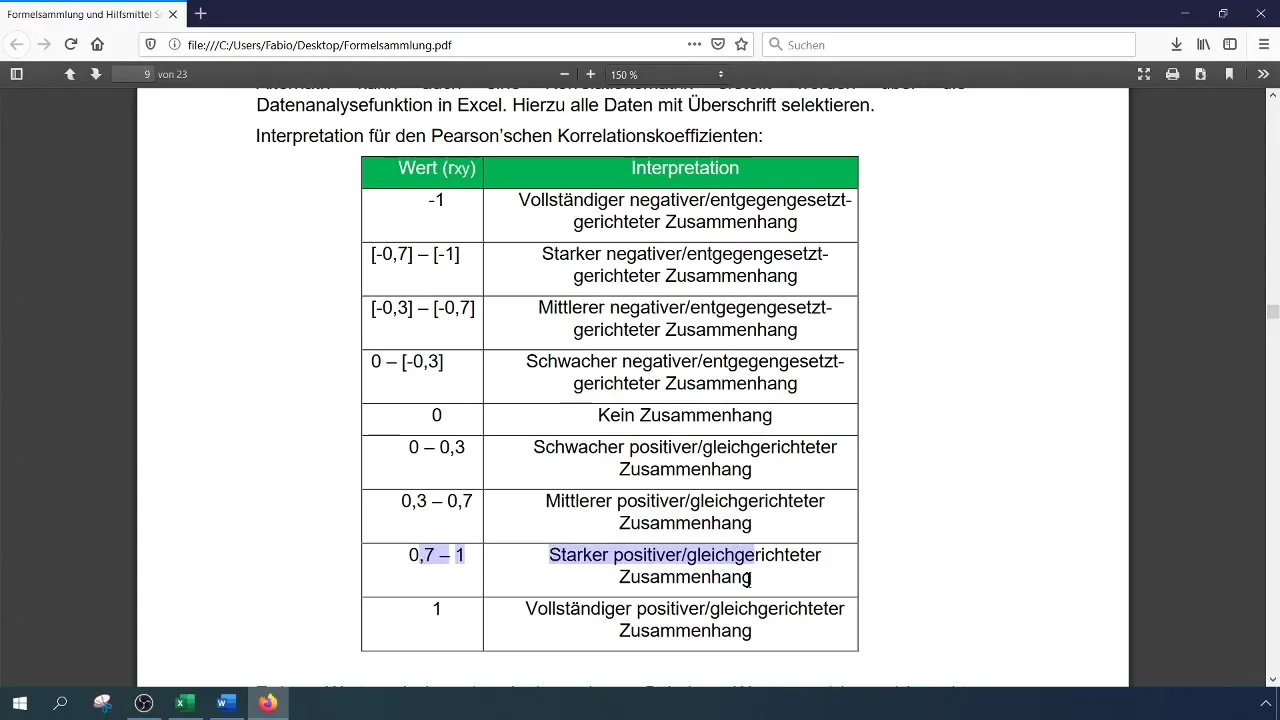
Til slutt er det viktig å tolke resultatene. Verdier over 0,90 indikerer en sterk positiv sammenheng, noe som betyr at en økning i en omsetningskategori følger med en økning i en annen omsetningskategori. I dette tilfellet er forholdet mellom smarttelefon- og bærbare datamaskinomsetninger ekstremt sterkt.

Oppsummering

I denne veiledningen har du lært hvordan du kan beregne og tolke Pearsons korrelasjonskoeffisient i Excel. Gjennom forskjellige metoder har du blitt vist flere måter å kvantitativt og visuelt presentere korrelasjonen mellom variablene på. På denne måten har du muligheten til å analysere virkelighetsdata og trekke viktige forretningsmessige innsikter.